盾构隧道邻近建筑物施工的地面变形分析及预测

朱逢斌 缪林昌

(1东南大学岩土工程研究所,南京210096)(2苏州科技学院土木工程学院,苏州215011)

随着地铁建设热潮的不断持续与升温,出现了越来越多的地铁盾构隧道邻近既有建筑物施工的工况.地面建筑物常因遭受隧道开挖引起的地层变位而破坏,相关研究工作主要集中在隧道开挖引起的地层变形及其导致的既有建筑物破损状况2个方面.关于前者的研究成果较多,而且被广泛应用于实际工程中;而关于后者,较为可行的研究方法主要是数值计算法与实测法.

文献[1-4]采用二维有限元法研究了隧道施工对地表结构物的影响效应,探讨了地下隧道与地表构筑物之间的共同作用问题,但无法真实考虑上部结构刚度对地层变形的约束效应.隧道-土体-建筑物之间的相互作用问题具有三维特性.文献[5-8]利用三维有限元技术对隧道开挖引起的地层变形及其对邻近建筑物的影响效应展开了弹性(或弹塑性)分析.

本文采用理论分析和三维数值计算方法,系统研究了不同影响因素作用下,地面既有多层框架结构建筑物对盾构隧道开挖导致地层变形的影响效应及影响规律.

1 工程实例分析

1.1 工程概况

实测盾构区间位于深圳地铁一号线续建工程西乡站至海湾中学段,区间隧道施工示意图见图1.该区间隧道左、右线均为直线,其间距为23 m,左线区间长度为257.115 m,右线区间长度为271.150 m.设计采用圆形隧道,内径为5.4 m,外径为6 m,宽度为1.5 m,共分为6块.管片采用C50防水混凝土,并设计成错缝拼装形式[9].

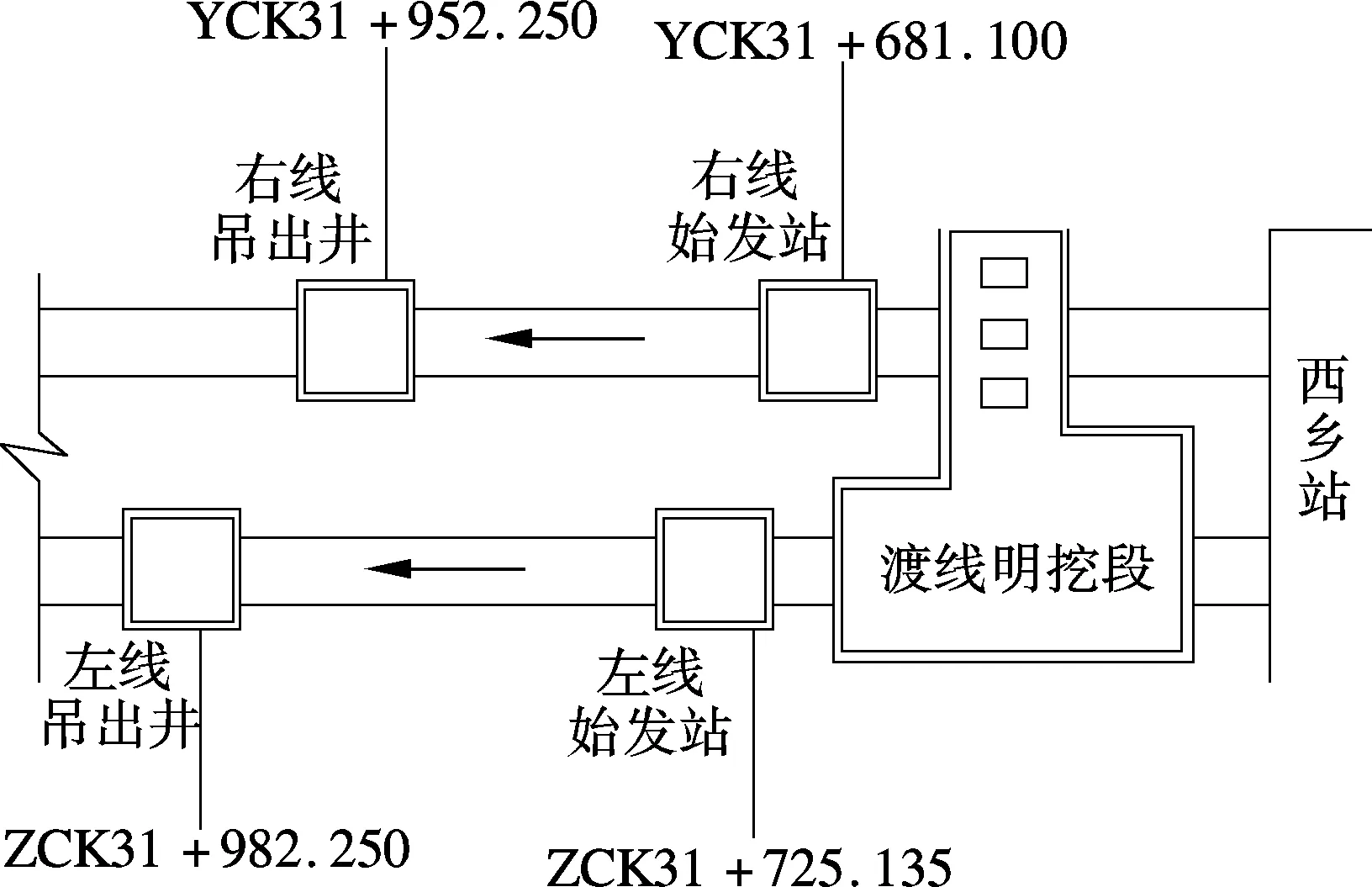
图1 区间隧道施工示意图

实测盾构施工段的左线隧道边线距南侧的碧海湾小区仅10 m左右.该小区4号楼为层高3 m的7层钢筋混凝土框架结构,由现浇柱、梁、板及柱下单桩基础构成,其平面尺寸为20 m×14 m,柱截面尺寸为500 mm×500 mm,梁截面尺寸为200 mm×300 mm,双向板厚100 mm,均采用C25混凝土浇筑.桩长14.7 m,截面尺寸为500 mm×500 mm,由C30混凝土浇筑.图2为楼层平面布置示意图.图中,①～⑤表示横向建筑轴线,A～D表示纵向建筑轴线.

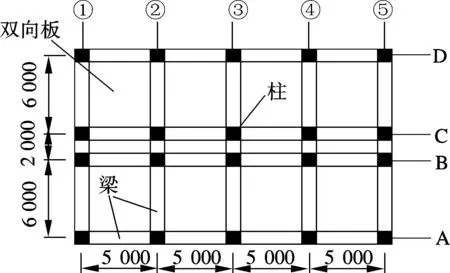
图2 楼层平面布置示意图(单位: mm)

1.2 数值分析模型

1.2.1 模型范围及边界条件

因左、右线隧道相距较远,两者间相互影响很小,故分析中选取左线隧道进行模拟施工.该隧道内径埋深19 m,衬砌外注浆层厚度为0.2 m.三维数值模型尺寸及其布置示意图见图3.

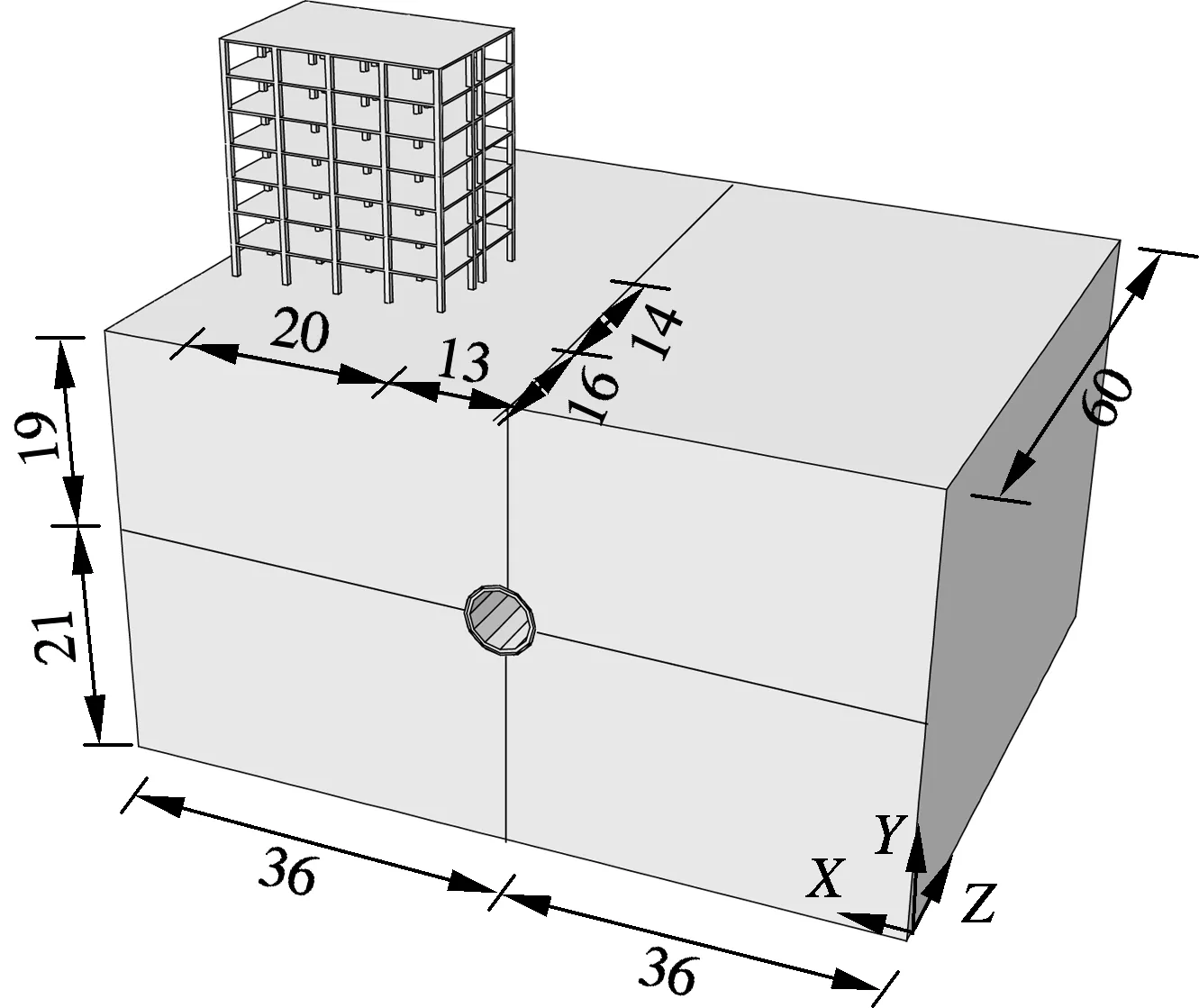
图3 数值分析模型示意图(单位: m)

对数值计算模型施加的边界条件如下:在X轴方向的左、右边界面上施加X向平移约束;在Z轴方向的前、后边界面上施加Z向平移约束;在Y轴方向的底面边界上施加X,Y,Z三向平移约束;顶面为自由边界.

1.2.2 模型参数

分析中所有模型材料均采用实体单元C3D8进行模拟.根据该场地工程地质勘察报告,土层厚度及计算参数见表1.计算中,将隧道衬砌与多层框架结构建筑物现浇梁、柱、板及柱下单桩基础均考虑为线弹性材料,且各土层的本构模型均采用Mohr-Column弹塑性模型.

考虑到接头对衬砌结构刚度有一定的削弱作用,将衬砌管片结构刚度折减0.15,则C50管片折减后的弹性模量为29.4 GPa.

1.2.3 模型隧道动态开挖模拟

按盾构区间隧道的实际施工工况,利用刚度迁移法,模拟盾构隧道分步开挖工况,共计40个开挖步,且单次开挖掘进1.5 m.数值试验中,每开挖一个进尺,便在开挖掌子面处施加推力0.35 MPa,在开挖洞壁周边施加注浆压力0.15 MPa,同时,激活管片层、注浆层单元,卸去注浆压力,掌子面推力则在开挖下一进尺施工步中卸去.如此循环往复,以模拟盾构的实际动态施工工况.此外,采用罚刚度法考虑桩土界面上的接触效应,其切向摩擦系数按土层条件取为0.3.

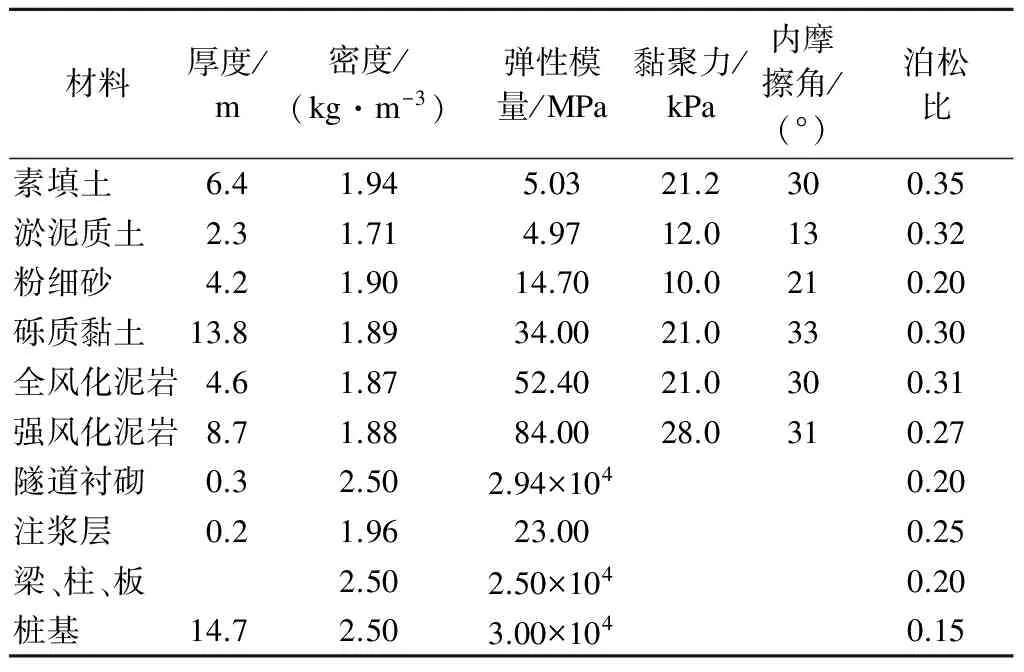
表1 模型材料参数

数值试验中,未考虑地下水渗流的影响,且计算中输入的是土体总应力抗剪强度指标.将计算得到的地面沉降视为盾构施工期沉降,故其可与盾构施工期间的实测沉降数据进行对比分析.

1.3 结果验证

施工现场监测得到横断面ZCK31+744处的最大地表沉降值为24.4 mm,且该沉降是由左线盾构掘进诱发的,故数值模型中仅考虑左线盾构施工工况是合理的.根据图1可知,横向监测断面距开挖起始断面(Z=0 m)约18 m.

由图4可以看出,当盾构推进至距开挖起始面30 m时,鉴于隧道左侧既有建筑物的约束作用,隧道左侧地表沉降发展稍迟滞于右侧地表.由图5可以看出,当盾构远离建筑物时,开挖面后方土体沉降趋于稳定,隧道两侧地表沉降分布几乎对称.由此可见,盾构推进至地面既有建筑物附近时,建筑物对周边地层变位具有一定的约束作用;而当盾构远离后,则可不考虑该约束作用.

由于施工监测获得的是横断面ZCK31+744处的最大地表沉降,故应采用数值模型中盾构开挖完成后相应监测断面处诱发的最大沉降与之进行对比分析.由图6可知,有限元计算与实测获得的横向地表沉降分布大致相同；但隧道中心线正上方的最大地表沉降值略有差异,有限元计算值(21.4 mm)比实测值(24.4 mm)小12.3%.

综上所述,三维数值计算结果与实测值能较好地吻合,表明各计算参数选取较合理,结果较可靠,该分析方法适用于盾构隧道近接既有建筑物施工的影响研究.

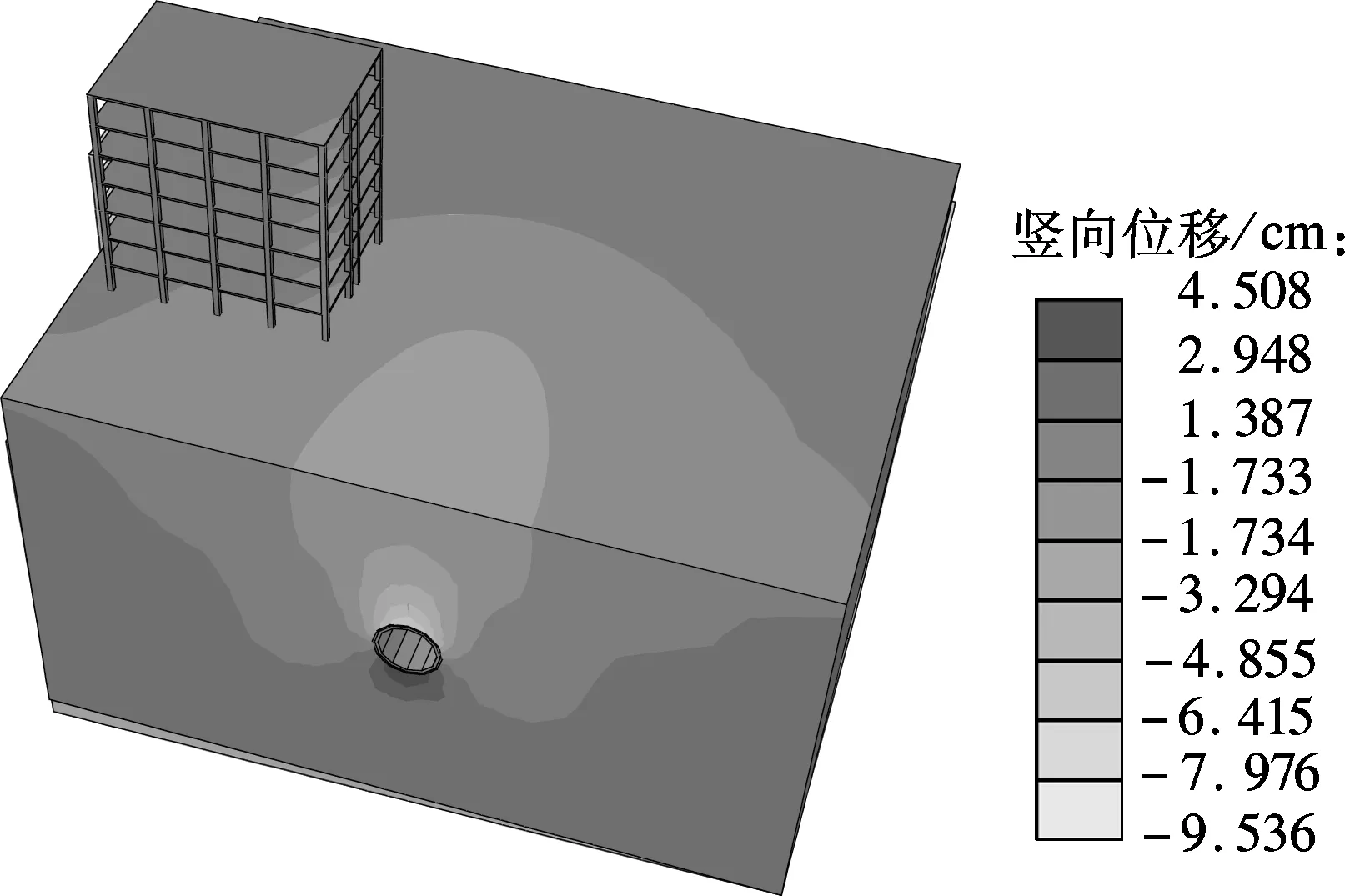
图4 隧道掘进30 m时地面沉降分布图

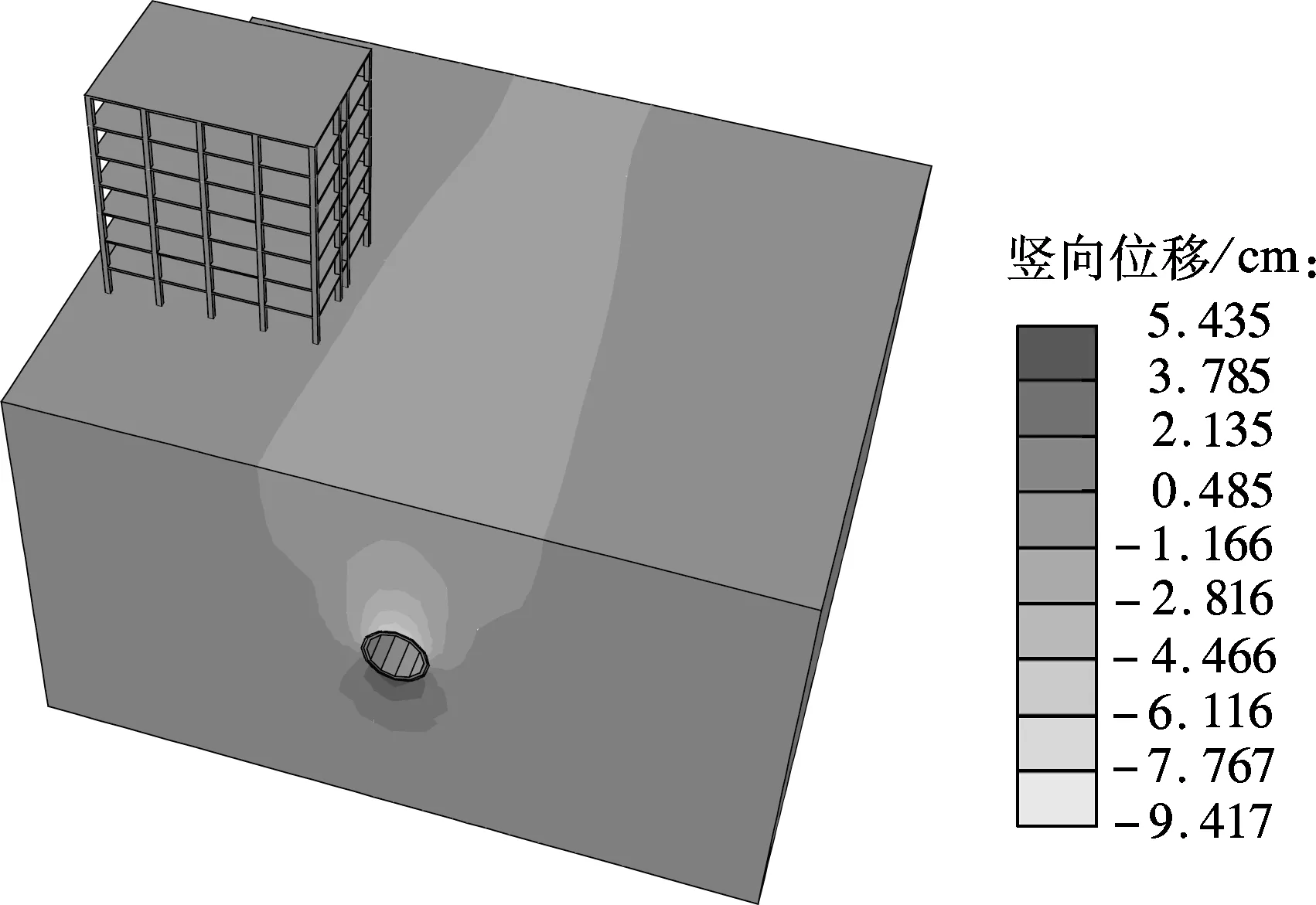
图5 隧道开挖完成时地面沉降分布图

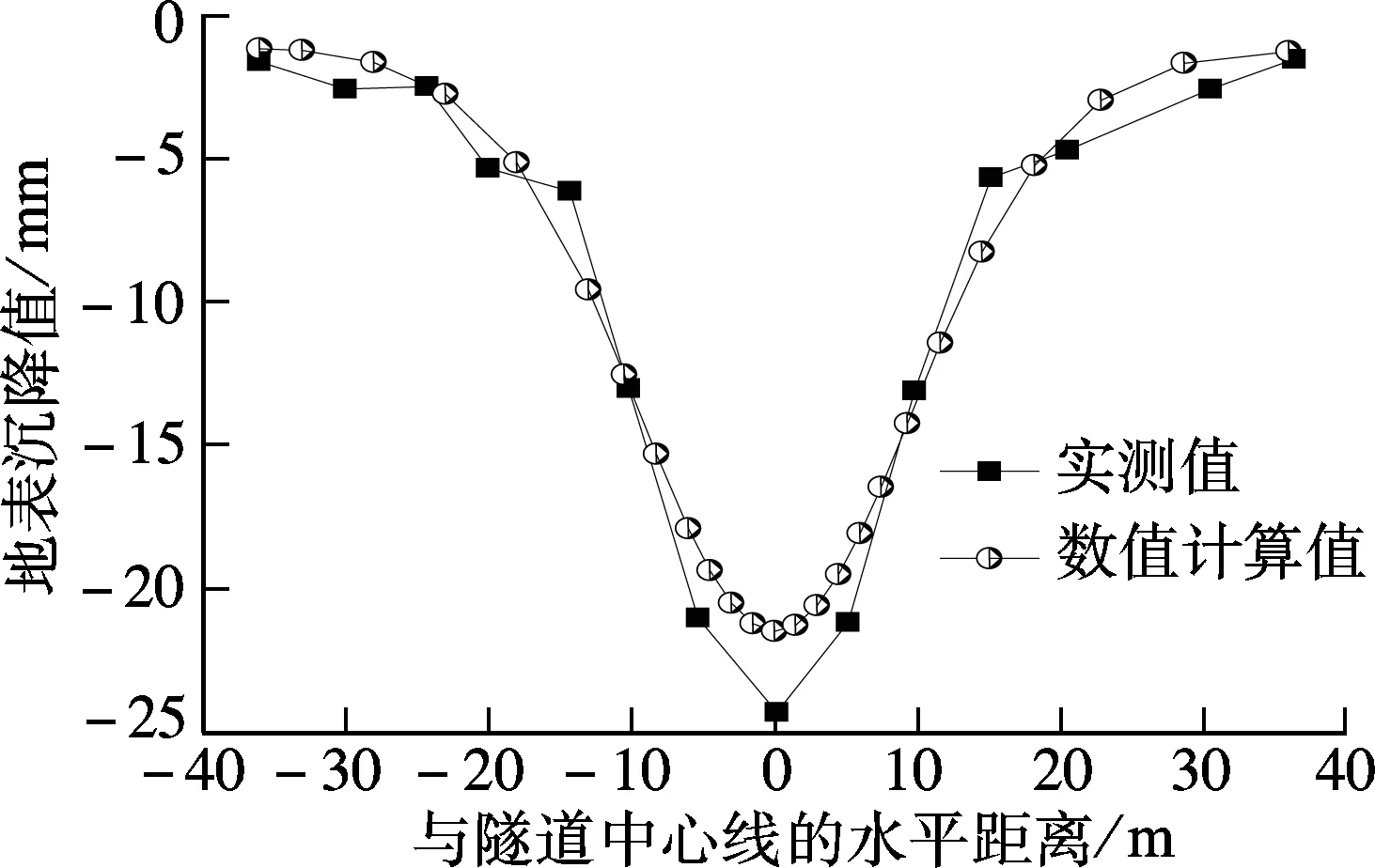
图6 横向地表沉降对比

2 建筑物对地面沉降的约束效应分析

2.1 建筑物基础形式的影响

拟增加民用建筑物中常用的柱下单独基础形式(埋深及边长均为1.5 m的方形单独基础),与验证实例中长度为14.7 m的柱下单桩基础进行对比分析(见图7).

为了充分考虑既有建筑物-土体-盾构隧道间的共同作用,研究建筑物对地表沉降的约束效应,以下分析中的沉降监测断面均取为建筑物横向分布范围内距起始开挖面24 m处的地表.

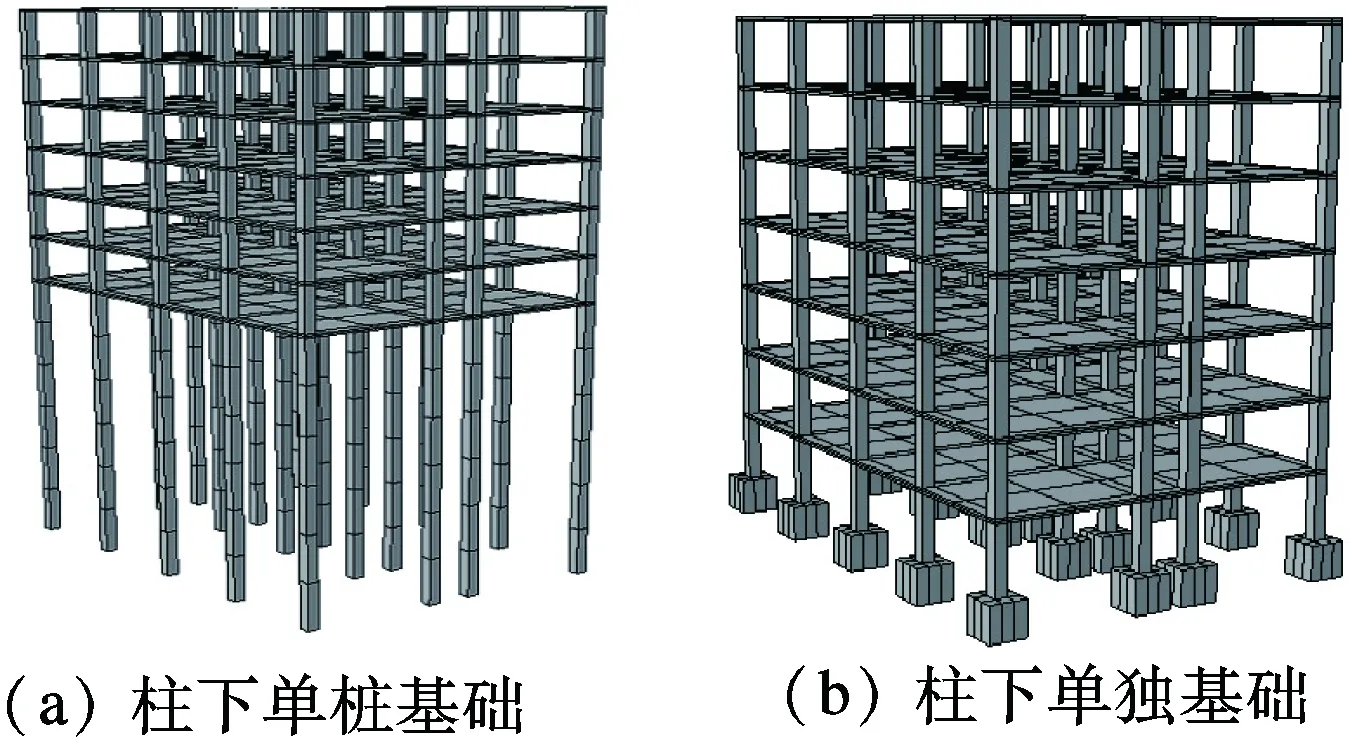
图7 基础形式对比

由图8可知,因基础形式不同,在建筑物横向分布范围(X=13～23 m)内的地表沉降曲线存在差异.与柱下单桩基础相比,柱下单独基础条件下盾构施工引起的地面沉降值较大,且沉降曲线斜率较大,导致上部结构出现较大程度的倾斜变形.其原因在于,桩基础约束了隧洞周边的深层土体沉降,传至地表的沉降有所减小.在建筑物横向分布范围以外,上述2种基础形式条件下盾构施工引起的地表沉降曲线几乎重合,说明在建筑物分布范围内柱下单桩基础较柱下单独基础能更好地约束地层变形.

图8 不同基础形式下的地表沉降

2.2 建筑物刚度的影响

在其他参数保持不变的前提下,通过改变多层框架结构楼层数量N(N=1,3,5,7),研究建筑结构刚度及自重对地表沉降的影响效应.针对多层框架结构建筑物，常采用柱下单独基础形式,以下分析中的数值计算模型均考虑采用柱下单独基础.

由图9可知,与地表不存在建筑物时的自由场地表沉降相比,在多层框架结构建筑物自重及刚度共同作用下,邻近盾构隧道开挖引起的建筑物横向分布范围内的地表沉降曲线明显变陡,建筑物向隧道方向倾斜趋势明显.此外,当楼层数增加至3层及以上时,建筑物自重和刚度的影响效应相当;当楼层数少于3层时,随着楼层数的增加,刚度对地表沉降的约束效应强于自重的增大效应.

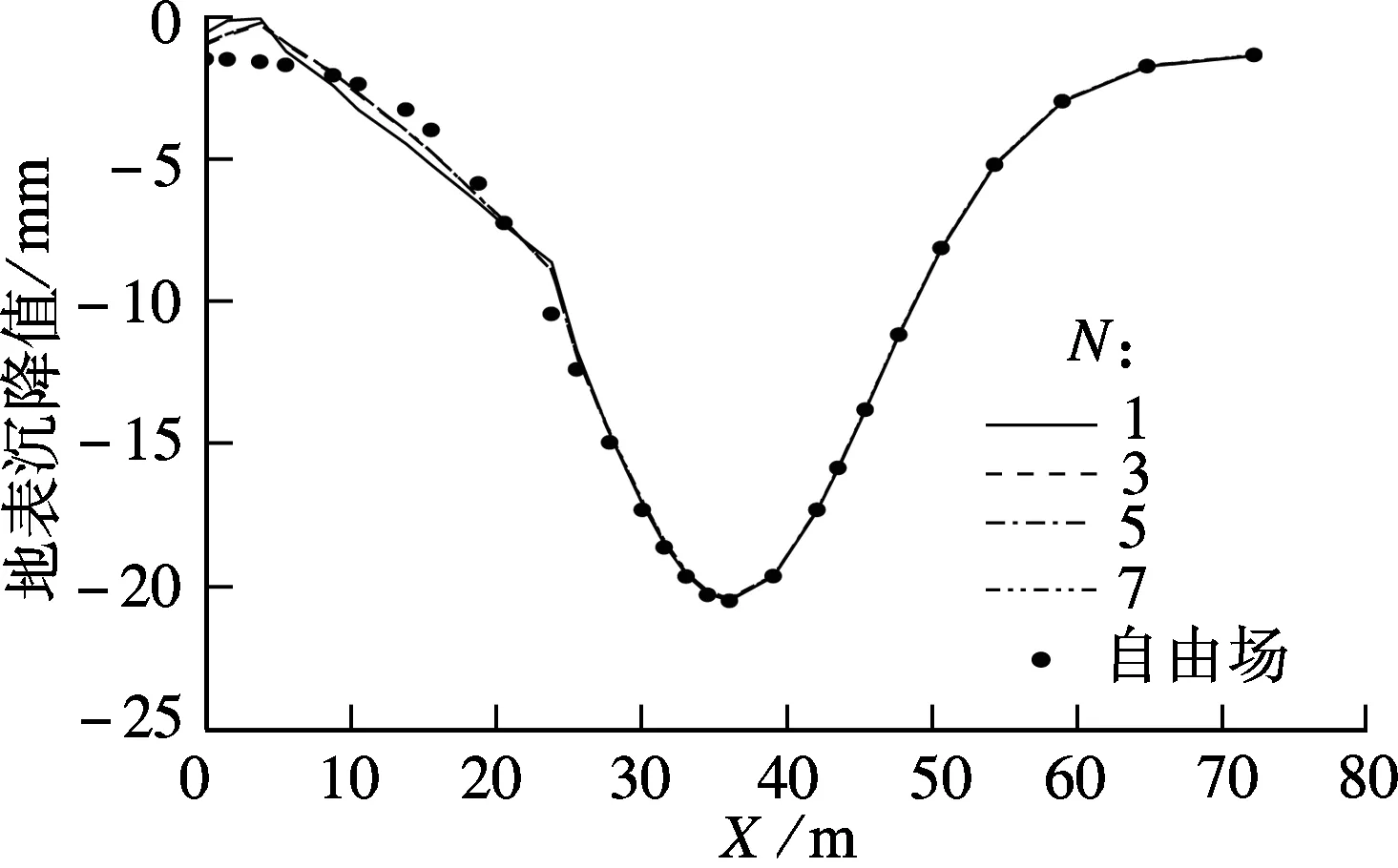
图9 不同建筑刚度下的地表沉降

2.3 建筑物长宽比的影响

在保持建筑物右侧山墙与隧道侧向间距不变的条件下,分别将X向柱间距调整为3,4,5 m,即长度L=12，16，20 m.因其沿隧道开挖方向宽度B=14 m,则长宽比L/B=0.86,1.14,1.43.

由图10可知,随着L/B的增大,建筑物横向分布范围内地表沉降曲线斜率逐渐变缓,右侧边缘(X=23 m)处的沉降值逐渐减小.这说明L/B越大,建筑物对地表变形的约束越强.而对于L/B较小的建筑物,在邻近盾构隧道开挖影响下,易发生朝向隧道的整体倾斜破坏.

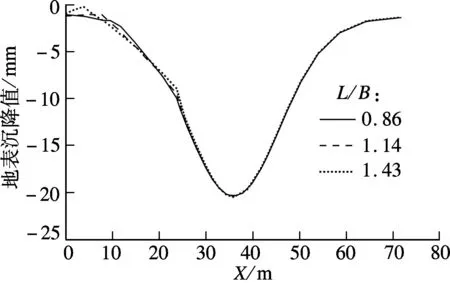
图10 不同建筑长宽比下的地表沉降

2.4 隧道埋深的影响

基于前述实例数值模型,将隧道埋深分别上移、下移一倍衬砌外径D,即考虑隧道埋深h=13,19,25 m时对地层变形的影响效应.

由图11可知,浅埋隧道(h=13 m)开挖对地层变形的影响范围虽然最小,但位于隧道左侧建筑物横向分布范围内的地表沉降曲线形态明显有别于右侧地表,且数值稍大.随着隧道埋深的增大,开挖影响范围亦增大,此时深埋隧道(h=25 m)开挖引起的地表沉降在隧道左右侧的分布形态几乎对称,表明地面建筑物对深埋隧道导致的地表沉降的约束作用减弱，即隧道埋深越大,开挖引起的地面沉降越接近于自由场条件.

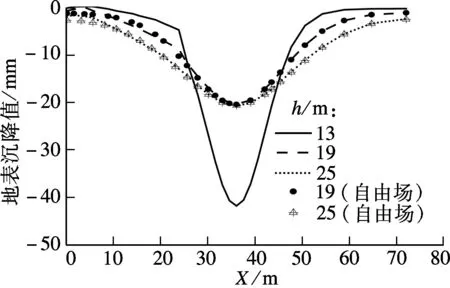
图11 不同隧道埋深下的地表沉降

2.5 隧道与建筑物夹角的影响

实际隧道有可能斜向穿越地面建筑物.因此,考虑将框架结构建筑物的横向中心线进行旋转,使其与隧道中心线的夹角θ=0°,30°,60°,90°(见图12),以研究隧道斜向穿越建筑物时的地表沉降规律.

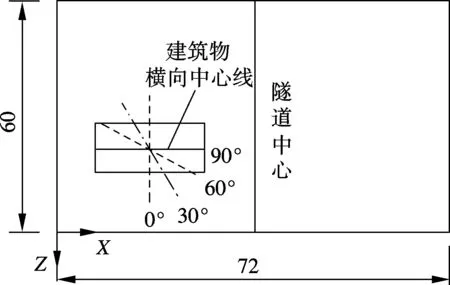
图12 隧道与建筑物夹角示意图(单位：m)

由图13可知,盾构隧道与建筑物的夹角θ越小,隧道中心线正上方的最大地表沉降值越小,且建筑物横向分布范围内的地表沉降曲线越平缓.

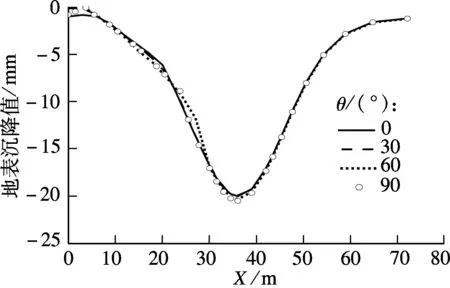
图13 不同夹角条件下的地表沉降

2.6 建筑物与隧道间偏心距的影响

如图14所示,当隧道与建筑物中心正交时,隧道中心线两侧地表沉降分布对称.受建筑物约束作用,隧道上方地表的沉降曲线几乎水平,且数值明显偏小.

当建筑物右山墙位于隧道拱顶的正上方时,地面建筑物的自重荷载作用加剧了隧道上方的地面沉降.当隧道右山墙位于隧道左侧边缘正上方时,因隧道开挖引起的土拱效应的支撑作用以及地面建筑物的约束效应,使地面沉降最大值接近于隧道正交穿越地面既有建筑物施工导致的最大地面沉降.当建筑物右侧山墙继续偏离隧道时,盾构开挖使建筑物开始朝隧道倾斜,隧道上方地面沉降值增大.

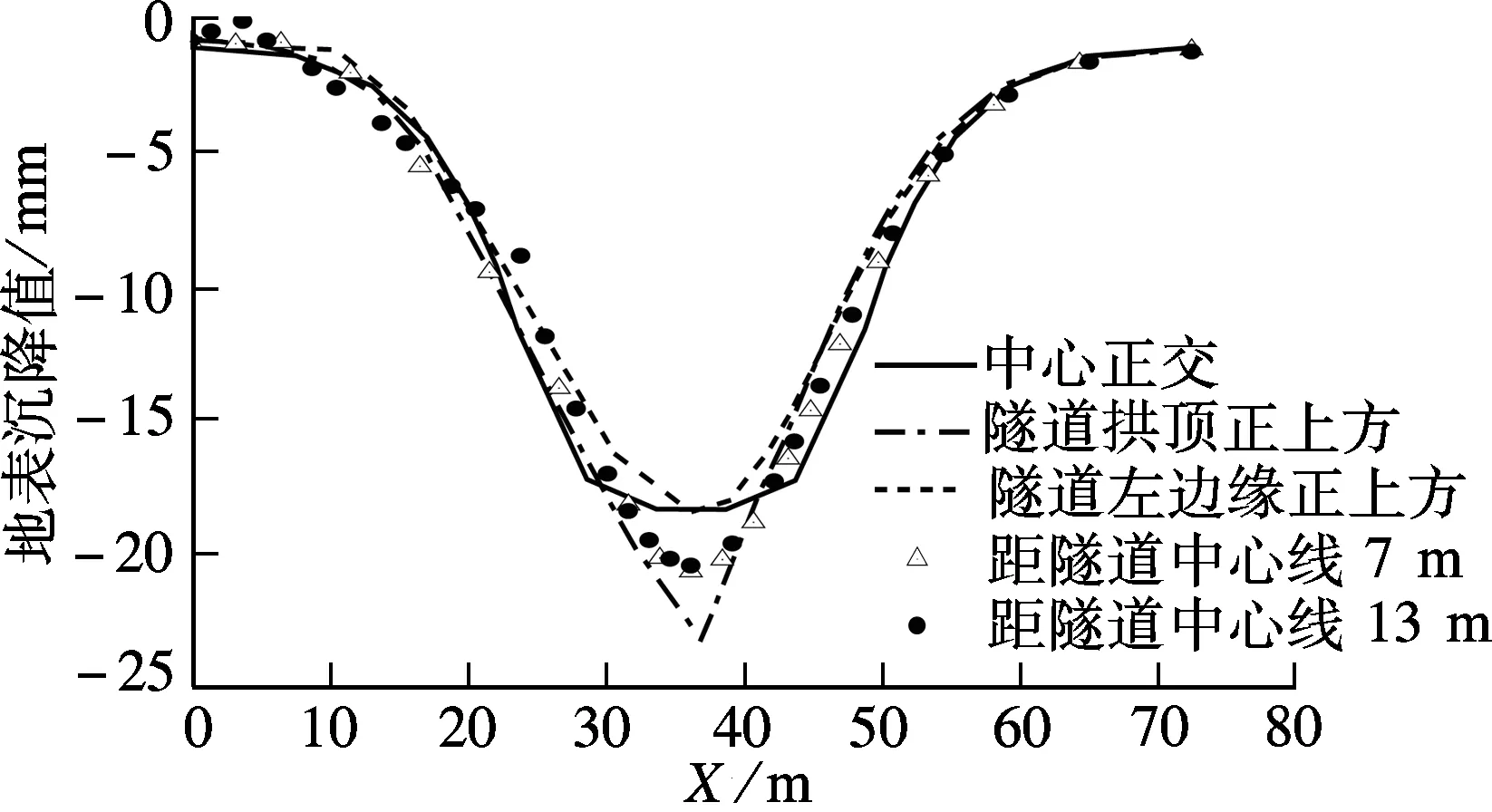
图14 不同偏心距下的地表沉降

3 地面沉降预测

建筑结构的刚度对隧道开挖导致的地表沉降具有明显的约束作用.若在地表沉降预测经验公式中引入建筑物刚度的约束效应,可提高经验公式预测结果的准确性,且更加符合工程实际.

在隧道与建筑物间存在偏心距的条件下,隧道开挖会导致地面产生以地面沉降反弯点为分界点的上拱与下沉变形(见图15).由此可得,地面下沉区与上拱区的挠曲比分别为

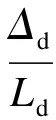
(1)

(2)

式中,Rd为下沉区挠曲比;Δd为下沉区挠度;Ld为下沉区长度;Ru为上拱区挠曲比;Δu为上拱区挠度;Lu为上拱区长度.

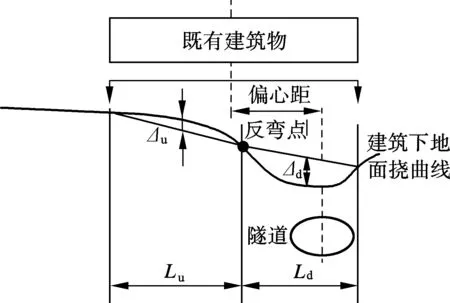
图15 建筑物下地面挠曲变形

为了利用自由场条件下的地面挠曲比来预测建筑物的挠曲比,Potts等[10]将建筑物等效为均质弹性梁,认为梁底面变形与地面协调一致,由此定义了建筑物挠曲比修正系数,即

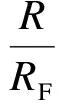
(3)

式中,MR为建筑物挠曲比修正系数;R为建筑物等效梁底挠曲比;RF为自由场条件下与建筑物等效梁相同位置处的地面挠曲比.

根据平面应变条件下大量的参数分析,确定了不考虑自重的建筑物因隧道开挖导致的挠曲比与其相对弯曲刚度的关系曲线(见图16).

图16 建筑物弯曲刚度与挠曲比关系曲线

考虑到实际建筑物为三维结构,需将建筑物沿隧道开挖方向的纵向长度B融入到不计自重的建筑物相对弯曲刚度中[11],即

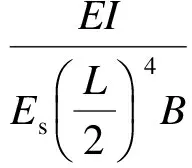
(4)

式中,ρ*为考虑纵向长度B的建筑物的相对弯曲刚度;E为不计自重的建筑物的弹性模量;I为不计自重的建筑物的惯性矩;Es为均质土弹性模量.

据此,首先利用三维有限元计算获得自由场条件下横向地表挠曲比RF.然后,根据图16所示的建筑物弯曲刚度与挠曲比关系曲线,按照式(4)中的ρ*,查得相应建筑物刚度影响下的修正系数MR.进而由式(3)得到考虑建筑物刚度约束效应的地表挠曲比R,并将其与相应的三维数值计算结果进行对比分析,判断考虑建筑刚度影响的地面挠曲比预测方法的有效性与适用性.

将三维建筑结构按其楼板层材料特性等效为图17所示的三维整体弹性梁.整体弯曲刚度由各楼板层刚度组合而成[12],则

(5)

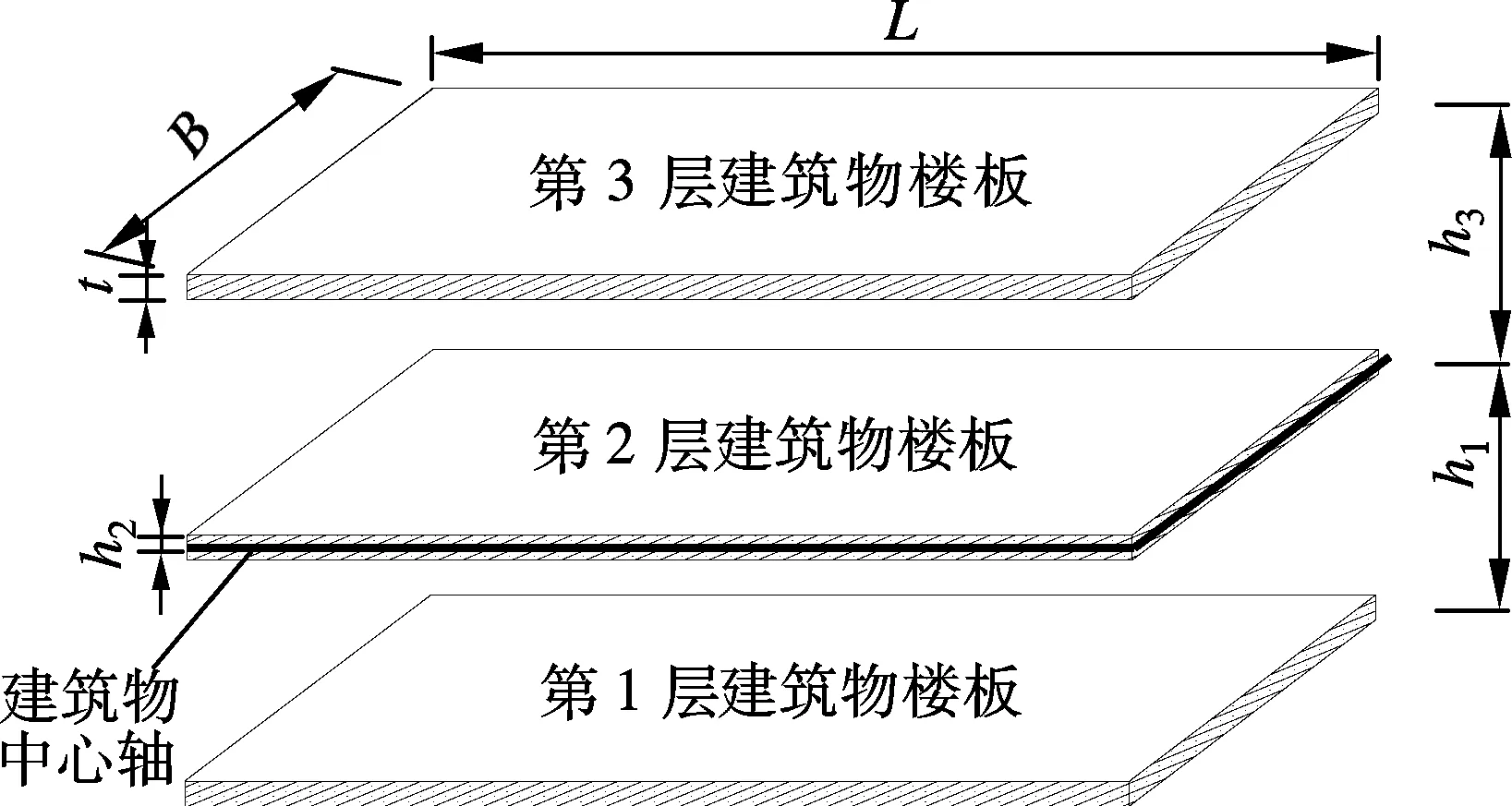
图17 建筑物等效梁示意图

式中，J为建筑物整体等效弹性梁弯曲刚度;Ec为楼板层弹性模量;If为楼板层截面惯性矩;Af为楼板层截面面积;hi为第i层楼板中性层至整体等效梁中性层的垂直距离;m为楼板层数.

根据本文工况,按式(4)和(5)计算得到的多层框架结构建筑物的整体等效梁弯曲刚度、相对弯曲刚度及挠曲比修正系数，结果见表2.

表2 建筑物等效梁刚度及相对刚度计算值

为了采用图16所示的设计曲线,以数值模型中的建筑物与盾构隧道为中心正交.据此,按式(1)和(3),并结合图16和图18,可得具有不同弯曲刚度的建筑物下地面挠曲比有限元计算值与经验公式预测值,结果见表3.由表可知,地面挠曲比的有限元计算值随建筑物弯曲刚度的增大而减小,且其值与经验公式预测值处于同一个数量级上,但前者的数值偏大.究其原因在于,有限元计算中考虑了建筑物的自重,而经验公式中则未考虑.

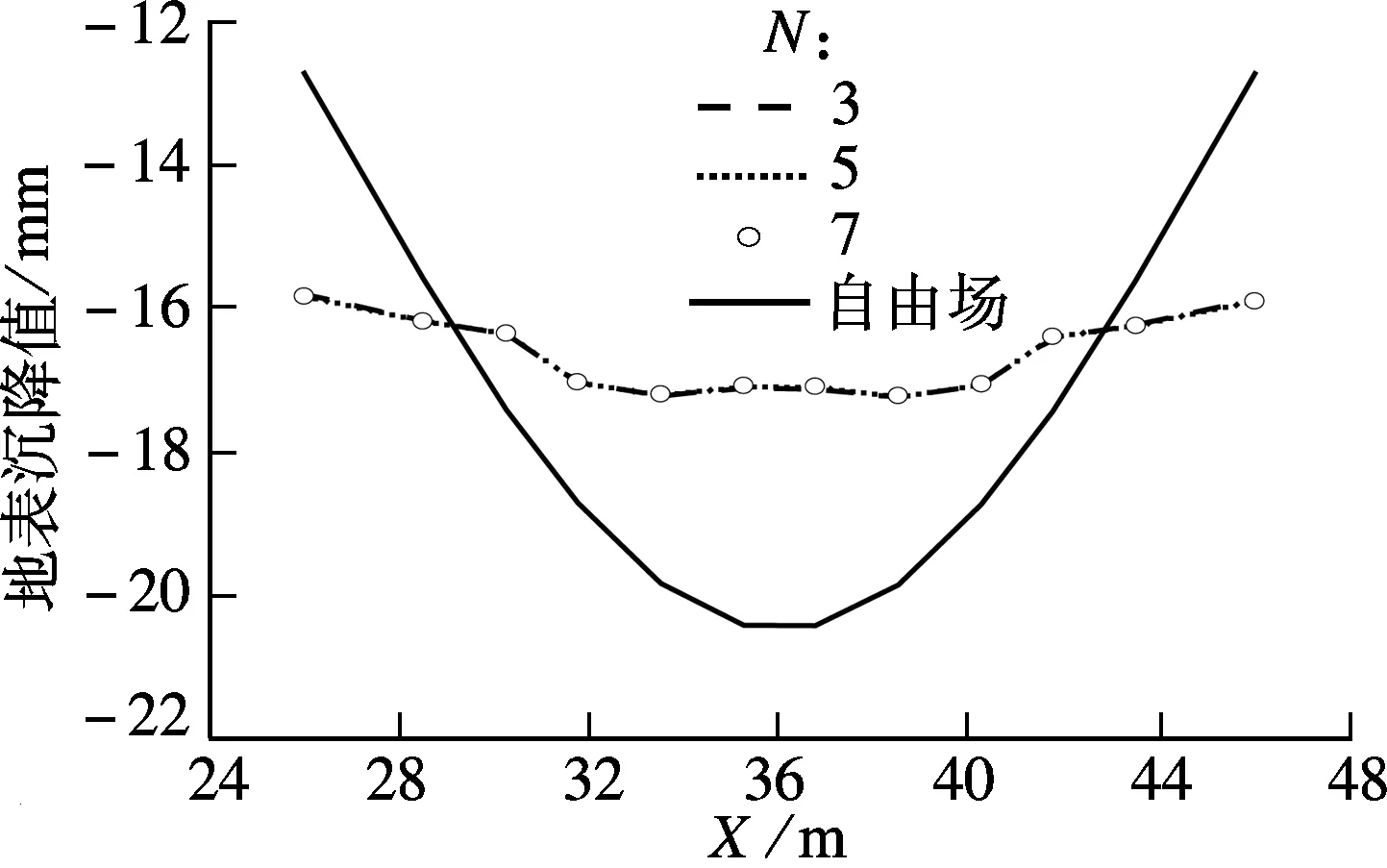
图18 建筑物下地表沉降的数值计算结果

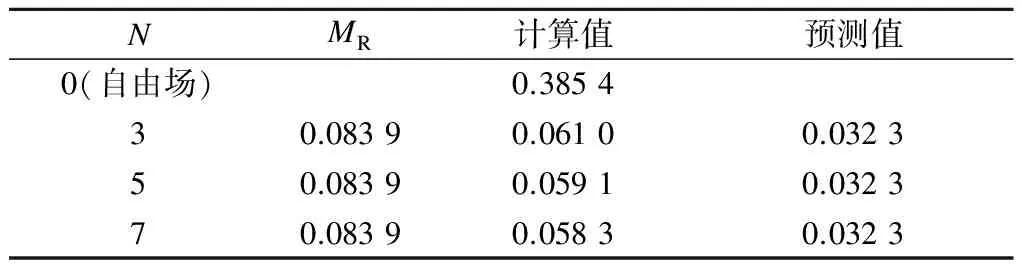
表3 建筑地面挠曲比的计算值与预测值

综上可知,考虑建筑物刚度影响的经验公式能方便、实用地预测建筑物下地面的挠曲变形.然而,由于该公式没有考虑建筑物的自重影响,往往会放大建筑物刚度对地面变形的约束效应.

4 结论

1) 地面既有建筑物对其分布范围内的地面沉降具有明显的约束效应,且在上部结构相同的条件下,桩基础对地面沉降的约束作用大于柱下单独基础.当建筑楼层少于3层时,楼层刚度对地表沉降的约束效应强于其自重的增大效应;而当建筑楼层增加至3层及以上时,建筑刚度及其自重对地表沉降的影响效应相当.

2)建筑物的长宽比越大,其对地表沉降的约束作用越强.长宽比较小的建筑物,较易发生朝向隧道的整体倾斜破坏.地面建筑物对较大埋深隧道开挖引起的地面沉降的约束作用较小,该地面沉降也更接近于自由场条件.

3) 当隧道与建筑物中心正交时,开挖引起的地面沉降最小.当建筑物山墙位于隧道拱顶的正上方时,则会加剧隧道上方的地面沉降.当山墙位于隧道边缘的正上方时,地面沉降最大值有所减小并接近于正交情况,且地面建筑物开始向隧道倾斜变形.

4) 考虑建筑物刚度的经验公式能方便、实用地预测建筑物下地面的挠曲变形,但因该公式未考虑建筑物的自重影响,往往会放大建筑物刚度对地面变形的约束效应.

)

[1] 王善勇,唐春安,王述红,等. 地铁开挖对地基沉降影响的数值分析[J]. 东北大学学报：自然科学版,2002,23(9): 887-890.

Wang Shanyong,Tang Chun’an,Wang Shuhong,et al. Numerical simulation and research of the influence on the excavation of the subway to the bade sedimentation [J].JournalofNortheasternUniversity:NaturalScience,2002,23(9): 887-890.(in Chinese)

[2] 于宁,朱合华. 盾构施工仿真及其相邻影响的数值分析[J].岩土力学,2004,25(2): 292-296.

Yu Ning,Zhu Hehua. The simulation of shield tunnel construction and analysis of its influence upon surrounding environments [J].RockandSoilMechanics,2004,25(2): 292-296.(in Chinese)

[3] 魏纲,裘新谷,魏新江,等. 邻近建筑物的暗挖隧道施工数值模拟[J]. 岩土力学,2009,30(2): 547-552.

Wei Gang,Qiu Xingu,Wei Xinjiang,et al. Numerical simulation of underground excavated tunnel construction of adjacent structure [J].RockandSoilMechanics,2009,30(2): 547-552.(in Chinese)

[4] Akhaveissy A H. Analysis of tunnel and super structures for excavation [J].ScientiaIranicaA,2011,18(1): 1-8.

[5] Mroueh H,Shahrour I. Three-dimensional finite element analysis of the interaction between tunneling and pile foundation [J].IntJNumerAnalMethGeomech,2002,26(3): 217-230.

[6] 彭畅,伋雨林,骆汉宾,等. 双线盾构施工对邻近建筑物影响的数值分析[J]. 岩石力学与工程学报,2008,27(S2): 3868-3873.

Peng Chang,Ji Yulin,Luo Hanbin,et al. Numerical simulation of effects of double-tube parallel shield tunneling on neighboring building [J].ChineseJournalofRockMechanicsandEngineering,2008,27(S2): 3868-3873.(in Chinese)

[7] Malek M,Sereshteh H,Mousivand M,et al. An equivalent beam model for the analysis of tunnel-building interaction [J].TunnellingandUndergroundSpaceTechnology,2011,26(4): 524-533.

[8] Liu J F,Qi T Y,Wu Z R. Analysis of ground movement due to metro station driven with enlarging shield tunnels under building and its parameters sensitivity analysis [J].TunnellingandUndergroundSpaceTechnology,2012,28(3): 287-296.

[9] 韩德元. 地铁盾构施工对邻近建筑物的影响研究[D]. 辽宁阜新: 辽宁工程技术大学土木与建筑工程学院,2010.

[10] Potts D M,Addenbrooke T I. A structure’s influence on tunneling-induced ground movements [J].ICEJournalofGeotechnicalEngineering,1997,125(2): 109-125.

[11] Franzius J N. Behavior of Buildings due to Tunnel Induced Subsidence [D]. London: Department of Civil and Environmental Engineering of Imperial College of Science,Technology and Medicine,2003.

[12] Timoshenko S.Strengthofmaterials.Part1 [M]. London: D. Van Nostrand Co. Inc.,1957: 217-224.