硅微陀螺正交校正结构设计与试验
2013-03-22倪云舫李宏生黄丽斌赵立业
倪云舫 李宏生 黄丽斌 赵立业
(东南大学仪器科学与工程学院,南京 210096)
(东南大学微惯性仪表与先进导航技术教育部重点实验室,南京 210096)
硅微陀螺相较于传统陀螺具有体积小、功耗低、可批量生产等优势,经多年发展已实现了中低精度的应用,目前正向高精度发展,以应用于战术级导航制导[1-3].正交误差是限制硅微陀螺性能提高的重要因素之一,主要是由加工误差导致的结构不对称和不等弹性所引起的[4].有限的工艺水平条件下,正交误差的大小在一定程度上是不可控的,极大影响着结构成品的可利用率.正交信号与有用信号存在90°相位差,故一般采用同步解调法将其分离.但正交信号幅值通常远大于有用信号,对前端电路动态范围要求增大,限制了陀螺的分辨率和信噪比.同时,大的正交误差对解调相位精度要求很高,存在相差时,混入输出的正交成分将对陀螺的长期零偏稳定性和零偏温度稳定性造成很大影响.因此,一种理想的处理方式为从源头上抑制正交运动,使陀螺不输出正交信号[5],可采用如下3种方法:① 机械修调.即以激光微调等加工后处理手段,去除部分位置的部分材料,消除结构不对称和不等弹性.该法可以从根源上消除正交误差,但处理时间长、成本高,不适用于批量生产.② 闭环控制.即设计闭环控制电路,产生反馈力抑制正交运动.该法在闭环硅微陀螺中已被广泛采用,但获得好的校正效果需要精确的频率、相位和幅度控制.③ 静电修调.即基于静电-结构耦合效应,设计正交校正结构,利用直流电压和结构本身的驱动运动,产生与正交力等幅同频反相的静电力来抑制正交运动.与前述方法相比,该法无需频率和相位控制,成本低、可移植性高,具有很大的实用价值.
静电修调本质上是通过引入非理想的静电刚度分布来平衡非理想的结构刚度分布,与杯形、环形陀螺中使用的正交控制方法原理相通,但在线振动式Z轴硅微陀螺中的应用于近几年才见报道[6-9].静电修调的关键在于正交校正结构设计.本文首先分析了静电修调原理,进而从电极形式、布局方式、参数优化3方面探讨校正结构设计问题,最后在自主研制的硅微陀螺上加以应用,试验证明结构具备预期的校正能力.
1 校正原理
硅微陀螺的正交误差主要是由结构不等弹性引入驱动X方向和检测Y方向之间的耦合刚度kyx而引起的,存在正交误差时结构运动微分方程可表示为
(1)
(2)


(3)

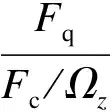
(4)
静电修调原理为:利用Fq与x成正比的特点,设计校正结构,使在加载直流电压时,能够利用驱动振动产生的频率和相位与x自然匹配,幅值可由电压值调节的Y向校正力,抵消正交力Fq,抑制正交运动,消除正交信号.其校正原理结构示意图如图1所示.
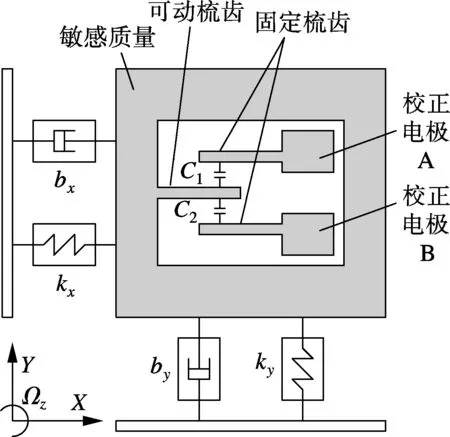
图1 静电修调校正原理结构示意图
可动梳齿为敏感质量的一部分,固定梳齿连接校正电极A和B,施加直流电压VA和VB.电容C1和C2是敏感质量位移x,y的函数,存储的静电场能为
(5)
式中,n为电极组数;ε为介电常数;h为厚度;l0,d0为可动梳齿和固定梳齿间的初始交叠长度和间隙.当敏感质量沿X向运动,且y≪d0时,校正电极产生的作用在敏感质量的X,Y向的静电力Fex,Fey为

(6)
fey中包含与x成正比的部分,构成的静电耦合刚度为
(7)
当keyx与kyx等值反号时,Fey中与x成正比的部分可抵消Fq,实现正交校正.结构耦合刚度kyx存在正、负2种可能:当kyx为正时,可取VA>VB或只施加电压VA;当kyx为负时,可取VA 校正结构电极的主要设计原则为:① 可动梳齿置于具有X,Y两个方向自由度的敏感质量上;② 电容量与驱动运动x成正比;③ 在Y方向上,动齿两侧的电场能量不平衡,当检测运动y≪d0时,产生的Y向静电力与电容量成正比. 若采用规则形状电极,可用的主要有平板电容式和梳齿电容式2种,如图2所示.平板电容式结构简单,但更适用于表面硅微机械加工的陀螺.在体硅微机械加工中,结构锚点与衬底键合区的面积不能太小,每一个电极B需要独立键合区时,电极在敏感质量上的可布组数很少,校正大的正交误差时需要很大的直流电压.梳齿电容式可以缓解这一问题,通过在间隙d0的另侧附加大间隙pd0(p为间隙比),使多组电极B共用一个键合区,较为适用于体硅微机械加工的陀螺. 图2 2种结构形式的正交校正电极 图2中梳齿电容式电极构成的静电耦合刚度为 (8) 对比式(7)可见,大间隙的引入(p>1)减小了单组电极的静电耦合刚度,但该形式电极的可布组数n大于平板电容式,可增大总静电耦合刚度.当敏感质量在Y向上的尺寸为mm量级,键合区最小宽度大于50 μm时,梳齿电容式电极的校正能力可达平板电容式的1.8倍以上. 单个校正电极产生的静电力中,除有用的校正力外,还包括其他附加干扰力.为简化分析,设 (9) 图2中梳齿电容式电极产生的X,Y向静电力为 (10) 可见,除与x成正比的Y向校正力外,产生的静电力中还包含与结构运动无关的X,Y向常值力.为消除这部分力的影响,设计电极布局方案如图3(a)所示的,此时静电力的分布如图3(b)所示. 图3 正交校正电极布局设计 记左上方校正电极产生的X,Y向静电力为Fex,UL,Fey,UL;右上方校正电极产生的X,Y向静电力为Fex,UR,Fey,UR,则有 (11) 可见,除有用校正力外,其余静电力在作用于敏感质量时相互抵消.下半部分电极分析方法与上半部分相同.上、下校正电极的静电力Fey,U,Fey,D综合为 (12) 总校正力Fey,qc以及构成的总静电耦合刚度keyx为 (13) 在有限的直流电压条件下,静电耦合刚度keyx的大小决定校正能力的强弱.由式(13)可见,影响keyx的结构参数有厚度h、间隙d0、组数n以及大小间隙比p.增大p可增大单组校正电极的keyx,但同时也将减少组数n.记敏感质量可用于布置校正电极的Y向尺寸为Ly,梳齿宽度为w,则可布组数n约为 (14) 结合式(13),p值对keyx的综合影响为 (15) 即在一定的h,d0,w条件下,p值通过常量γ来影响keyx的大小.受加工工艺对深宽比的限制,h和d0一般根据工艺条件进行取值.若取d0=4 μm,则不同w条件下,p值对常量γ的影响如图4所示.可见,对p进行合理取值可在有限的Ly条件下使校正结构构成的keyx最大化.当w取为4,6,8 μm时,p的最优取值分别为2.36,2.49,2.61. 图4 常量γ与p值的关系 在东南大学自主研制的某型双质量硅微陀螺[10]上进行正交校正结构设计.采用梳齿电容式电极以及图3所示的布局方案.双质量硅微陀螺结构示意图以及校正电极局部电镜照片如图5所示. 构成双质量硅微陀螺的2个单质量结构为全解耦形式,通过连接2个驱动框架的折叠梁实现弹性耦合.在敏感质量的内部设计正交校正结构,两侧结构呈180° 旋转对称.陀螺结构单个敏感质量约0.5 mg,在每个敏感质量中心各设计45组正交校正电极,电极参数为间隙4 μm,p值为2.4.由式(4)、(13)可知,校正等效输入角速度为Ωq的正交误差所需直流电压为 (16) 图5 双质量硅微陀螺结构及校正电极局部电镜照片 当驱动频率小于4 kHz时,在最大可施加直流电压为12 V的条件下,所设计的正交校正结构理论上具备校正405 (°)/s正交误差的能力. 采用体硅微机械加工工艺加工带正交校正的双质量硅微陀螺结构,以陶瓷管壳进行真空封装.正交校正过程为:令驱动回路正常工作,零角速度输入,观察输出正交信号,由其大小推算Ωq值,由其与驱动信号的相对相位关系判断kyx的正负;根据表头的Ωq值和驱动频率,由式(16)估计校正所需的直流电压平方差,根据kyx的正负,选择合适的校正电极施加直流电压;最后根据输出正交信号大小的变化进行微调,直至正交信号被完全消除. 取正交误差较大的某表头进行试验.校正前信号如图6(a)所示,图中,上方为驱动速度信号,下方为输出信号,在相位上滞后驱动速度信号约为90°,主要为正交信号,且kyx为正.由电路相关参数推算得Ωq约为354 (°)/s,驱动频率约3.8 kHz,由式(16)可知,校正所需直流电压平方差约为119.5 V2.由kyx为正,选择校正电极A施加直流电压10.9 V,观察输出发现,正交信号大幅减小但仍存在.增大直流电压至11.6 V后,正交信号被完全消除,信号如图6(b)所示,残余信号与驱动速度信号近似为同频同相关系,即为与有用信号同频同相的偏移误差部分.实际校正使用直流电压平方差约为134.6 V2,大于理论估计值,这可能是由于加工过刻蚀导致的梳齿间隙d0增大等非理想因素造成的. 图6 校正前后的驱动速度信号和输出信号 硅微陀螺的正交校正方法中,静电修调相对于其他方法具有实现简单、对电路无特殊要求等优势.合理设计校正结构可实现以直流电压进行正交校正.电极结构形式使其具备校正功能,合理的布局方式能够消除伴随校正力出现的附加静电力,结构参数优化使在有限的芯片面积内可实现校正能力的最大化.在自主研制的双质量硅微陀螺中设计的正交校正结构成功实现了利用11.6 V直流电压校正等效输入角速度为354 (°)/s的正交误差,其校正能力略小于但接近设计值,证明了正交校正结构设计的正确性. ) [1] Shkel A M, Horowitz R, Seshia A A, et al. Dynamics and control of micromachined gyroscopes[C]//ProceedingsoftheAmericanControlConference. San Diego, USA, 1999: 2119-2124. [2] Geiger W, Bartholomeyczik J, Breng U, et al. MEMS IMU for AHRS applications[C]//IEEE/IONPositionLocationandNavigationSymposium. Monterey, USA, 2008: 225-231. [3] Lapadatu D, Blixhavn B, Holm R, et al. SAR500-A high-precision high-stability butterfly gyroscope with north seeking capability[C]//IEEE/IONPositionLocationandNavigationSymposium. Indian Wells, USA, 2010: 6-13. [4] Yang Bo, Wang Shourong, Li Hongsheng, et al. The coupling error analysis of the decoupled silicon micro-gyroscope[C]//IEEE5thInternationalConferenceonNano/MicroEngineeredandMolecularSystems. Xiamen, China, 2010: 356-361. [5] Saukoski M, Aaltonen L, Halonen K A I. Zero-rate output and quadrature compensation in vibratory MEMS gyroscopes[J].IEEESensorsJournal, 2007,7(12): 1639-1652. [6] Zaman M F, Sharma A, Hao Zhili, et al. A mode-matched silicon-yaw tuning-fork gyroscope with subdegree-per-hour allan deviation bias instability[J].JournalofMicroelectromechanicalSystems, 2008,17(6): 1526-1536. [7] Sharma A, Zaman M F, Ayazi F. A sub-0.2 °/hr bias drift micromechanical silicon gyroscope with automatic CMOS mode-matching[J].IEEEJournalofSolid-StateCircuits, 2009,44(5): 1593-1608. [8] Chaumet B, Leverrier B, Rougeot C, et al. A new silicon tuning fork gyroscope for aerospace applications[C]//SymposiumGyroTechnology. Karlsruhe, Germany, 2009: 1.1-1.13. [9] Tatar E, Alper S E, Akin T. Effect of quadrature error on the performance of a fully-decoupled MEMS gyroscope[C]//IEEE24thInternationalConferenceonMicroElectroMechanicalSystems. Cancun, Mexico, 2011: 569-572. [10] 殷勇,王寿荣,王存超,等.结构解耦的双质量微陀螺仪结构方案设计与仿真[J].东南大学学报:自然科学版,2008,38(5):918-922. Yin Yong, Wang Shourong, Wang Cunchao, et al. Structural scheme design and simulation of structure-decoupled dual-mass MEMS gyroscope[J].JournalofSoutheastUniversity:NaturalScienceEdition, 2008,38(5): 918-922. (in Chinese)2 校正结构设计
2.1 电极形式

2.2 布局方式



2.3 参数优化



3 双质量硅微陀螺正交校正结构设计
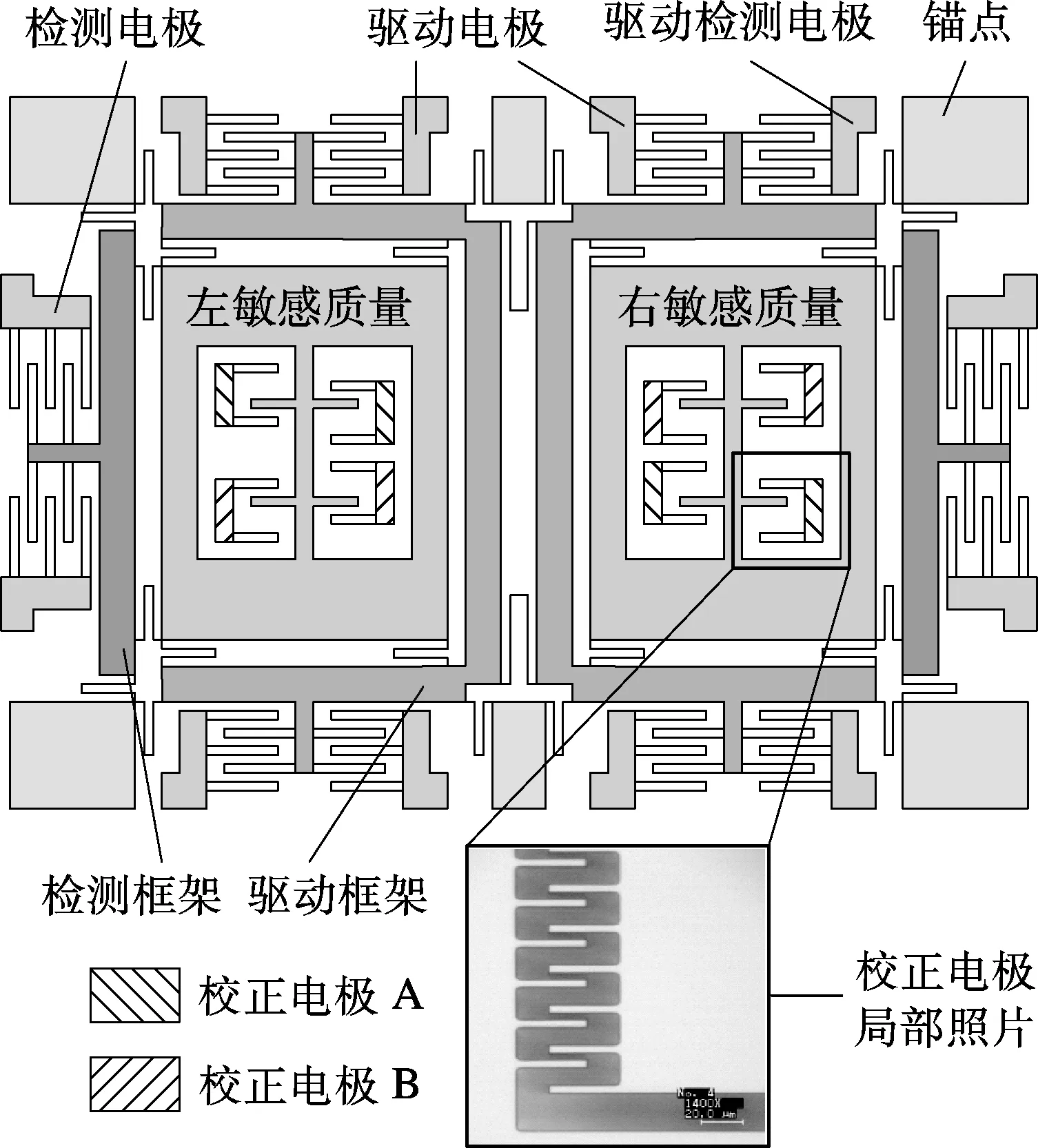
4 加工与试验

5 结语
