坐标测量机测量点通用可达性分析方法

曾德标， 郑国磊， 曾春玲

（1. 北京航空航天大学机械工程及自动化学院，北京 100191；2. 成都飞机工业（集团）有限责任公司技装设计所，四川 成都 610092）

坐标测量机接触式点位测量必须事先对测量点的可达性进行分析，一方面可以避免实际测量时发生碰撞，另一方面可以确定每个测量点的可达方向，为测量方向优化选择提供数据来源。测量点可达性分为静态可达性和动态可达性。静态可达是指在探针测尖已经接触测量点的状态下，探针、测头等坐标测量机的活动部件与工件、夹具等测量环境中的障碍物没有干涉。动态可达是指存在一条路径使得探针测尖在沿着该路径移动到触碰测量点的过程中，探针、测头等坐标测量机的活动部件与工件、夹具等测量环境中的障碍物不发生碰撞。动态可达的测量点一定是静态可达的，静态可达的测量点不一定是动态可达的。如图1所示，工件上的P1点是动态可达的，而P2点只是静态可达的。测量点可达性分析是计算机辅助检测规划领域中的研究热点之一。Spyridi等人[1-3]基于高斯图和闵可夫斯基操作精确地分析位于多面体零件平面上的测量点的可达性，但不适用于复杂零件。Spitz等人[4-6]将探针和测头抽象为线段和射线，并将零件网格化之后沿表面法矢扩大探针或测头半径的距离，以补偿探针和测头抽象为线段和射线之后的体积；最后，采用裁剪和深度缓冲算法，利用计算机图形硬件判断某一方向是否为可达方向。该方法做了过多的抽象简化，对于复杂零件的可达性分析并不十分准确。Limaiem和EIMaraghy[7,8]提出了一个可达性分析的同心球壳求交法，只考虑了探针和测头对可达性的影响，没有考虑测头座和立柱的影响。吴永清等人[9,10]将测头抽象为一条从测量点发出的射线，通过射线与零件体求交对该测量方向是否可达进行粗略判断；然后考虑测头长度的影响，根据测杆和测头在内检测面上的投影线段与内检测面边界的相交情况对测头方向做进一步的可达性分析；最后，考虑测头体积的影响，将测头抽象为一个顶点在测量点处的圆锥，若圆锥包围了前两步判断出的不可达方向，则此时圆锥的方向为不可达方向。该方法的计算量小，但是，在考虑测头长度的影响时依赖于测量点所在区域的形状，只能比较准确的处理规则的形状，对于不规则的形状，该方法的准确性较差。Chang和Lin[11]提出了判断测量方向是否可达的切平面投影法，只考虑了测尖和探针的直径，而没有考虑测头的直径，因此，在零件结构复杂的情况下判断容易出错。Álvarez等人[12,13]提出了基于最小距离计算的可达性分析方法，可以分析复杂零件的可达性，但只适用于球形测尖探针的可达性分析。

图1 测量点可达性

目前的测量点可达性分析方法一般只适用于图2(a)所示的球探针的静态可达性分析。实际上，探针除了常用的球探针，还有图2(b-f)所示的锥探针、半球探针、测量深孔和内腔的星形探针、测量薄壁件的柱探针、测量零件凹处、切口和沟槽等的盘探针等等，而且探针还能通过一些附件组合成更为复杂的组合探针，如球探针能够组合成类似星形探针的五方向探针等等。对于这些不常用的探针及组合探针，鲜有人提出有效的算法分析其用于测量时的可达性。因此，本文针对目前常见的各类型探针提出一个统一的测量点可达性分析方法，适用于任意类型和复杂程度的零件，而且既包括静态可达性分析，也包括动态可达性分析。

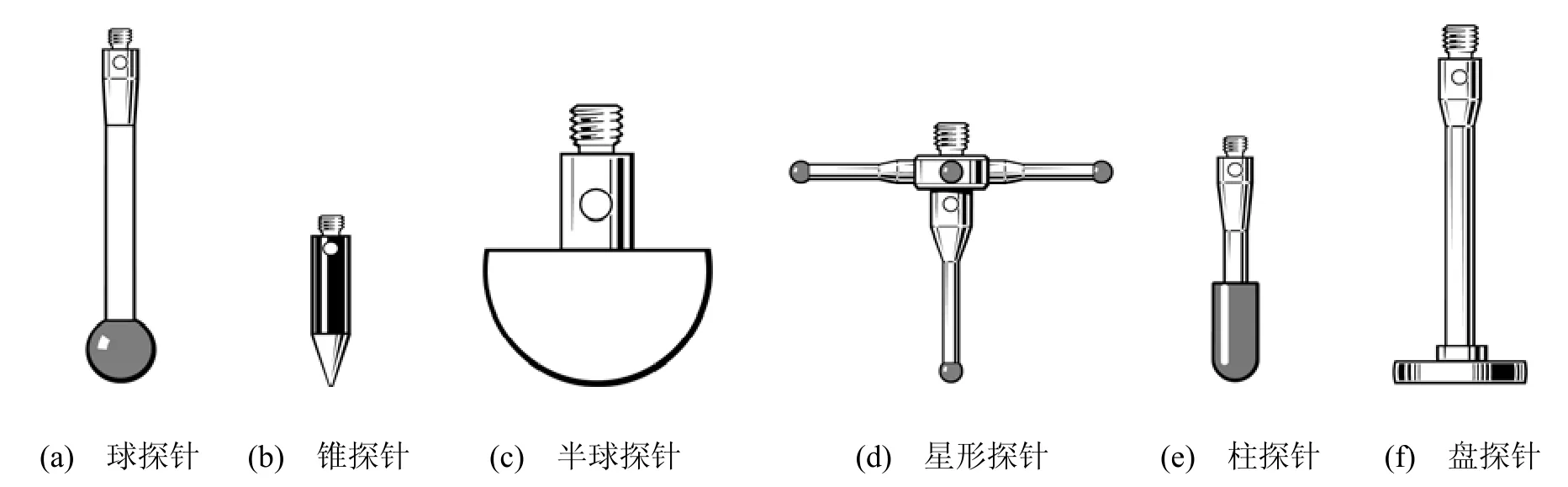
图2 探针类型

1 虚拟测量环境构建

为了提高测量点可达性分析的效率，坐标测量机一些活动部件的模型需要简化。用户通过圆球和圆柱两种基本几何体及其布尔运算建立探针、探针延长杆、测头、测头延长杆、测头座、立柱及附件的简化CAD模型。其中，探针测尖部分的CAD模型依据其真实形状和尺寸建立，因为探针在测量时与工件表面直接接触，简化的测尖模型会导致测尖与工件的干涉检查结果出错。坐标测量机其他部件的CAD模型也依据其真实形状和尺寸建立。坐标测量机的每个部件都有相应的配置表，记录该部件的参数、子部件以及与其它部件的连接端等信息，表1和表2分别为球探针和测头的配置表的结构。配置表由系统根据用户输入或选择的信息自动生成。部件的CAD模型和配置表存入测量设备库。

表1 球探针配置表结构

表2 测头配置表结构

在测量点可达性分析之前，首先由用户从测量设备库中选取所需的任意类型的测量机部件，系统自动生成坐标测量机的配置表，并存入测量设备库。坐标测量机配置表的结构如表3所示，表头中带括号的测量机部件是可选部件，其他部件是必选部件。用户也可直接调入以前生成的坐标测量机配置表，根据需要替换其中的一些测量机部件，而无需再一一选取测量机部件。然后由系统根据坐标测量机配置表自动载入测量机部件的CAD模型，并将各部件自动装配在一起，形成一个完整的测量机模型。测量机部件的自动装配根据各部件配置表中的连接端信息进行，例如探针与测头的自动装配方法为：探针连接端的同轴面与测头下连接端的同轴面建立同轴约束，探针连接端的接触面与测头下连接端的接触面建立接触约束。如果有探针延长杆，则将探针和探针延长杆、探针延长杆和测头分别自动装配在一起。测量机模型建立完成后，由用户载入工件和夹具的CAD模型，并将其安装在坐标测量机的测量平台上。最后，若测量所用的探针是星形探针或者是多个探针组成的组合探针，用户须指定测量时用的测尖。至此建立起了一个完整的虚拟测量环境，之后开始测量点的可达性分析。

表3 坐标测量机配置表结构

坐标测量机的测头有两个旋转角度：绕坐标测量机立柱轴线的旋转角α和竖直面内的摆动角β。测头的测量方向为旋转角与摆动角的组合(α,β)。旋转角α和摆动角β都有最小分度，因此，测量机支持的测量方向是有限和离散的。对于每一测量方向都一一分析其可达性，从而可以计算出每个测量点的全部可达方向。

2 静态可达性分析

静态可达性分析分为3大步骤：第1步是根据探针测尖的类型快速排除不可达方向；第2步是通过求交运算精确判断探针测尖是否与障碍物干涉；第3步是通过最小距离计算判断其他测量机活动部件是否与障碍物干涉。

设p为测量点，d为测量方向，n为零件表面在测量点处的外法矢，由零件体内指向体外，l为探针轴线方向，由探针测尖指向探针连接端，n与l的夹角为(n,l)。根据探针测尖类型快速排除不可达方向的方法如下：

1）球形和半球形测尖

如图3(a)所示，首先计算探针测尖在接触测量点p时球心到障碍物的最小距离，若最小距离小于测尖半径，则该测量点在任意测量方向下均不可达。在某个测量方向d下，若(n,l)＞90°，则d不是p的可达方向。

2）锥形测尖

如图3(b)所示，设锥形测尖的锥角为θ。在某个测量方向d下，若(n,l) ＞ 90° - θ/2，则d不是p的可达方向。

3）柱状测尖

如图3(c)所示，柱探针测量薄壁件轮廓上的测量点时，探针轴线方向须与零件轮廓面在测量点处的外法矢方向基本垂直，即图3中所示方向均为可达方向。

4）盘形测尖

盘形测尖是球形测尖对称削去两个球冠得到的，触测表面是球面。如图3(d)所示，设测尖的直径为φ，厚度为B，在某个测量方向d下，若(n,l)＞90°+arcsin(B/φ)，或(n,l)＜90°-arcsin(B/φ)，则d不是p的可达方向。

图3 快速排除不可达方向

对于在第1步中判断为可达的测量方向d，需要进一步检查在该测量方向下探针测尖是否与障碍物干涉。由于探针测尖在测量时与工件表面接触，因此，需要通过测尖部分的探针表面与测量点所在的工件表面及其邻近面求交来精确判断测尖与工件等障碍物是否存在干涉，若存在干涉，则测量方向d不是可达方向。对于球形测尖和半球形测尖，由于在第一步快速排除不可达方向时已经通过计算球心到障碍物的距离精确判断了干涉情况，故此步省略。

对于在第2步中判断为可达的测量方向d，需要进一步检查坐标测量机的各活动部件在该测量方向下是否与工件、夹具等测量环境中的障碍物干涉以最终确定d是否是测量点p的静态可达方向。此步借鉴了Álvarez的最小距离计算思想[12,13]，即：将工件、夹具等测量环境中的所有障碍物的表面离散成三角面片，依次计算探针的测杆、探针延长杆（若有）、附件（若有）、测头、测头延长杆（若有）、测头座及立柱的球形段/圆柱段的球心/轴线段到各三角面片的距离，若最小距离小于圆球/圆柱的半径加上一个安全冗余距离（与障碍物表面离散成三角面片的精度有关），则测量机部件与三角面片相交，测量方向d不是测量点p的可达方向。这里实际上将测量机部件非完整的球形段视为了完整的圆球，圆柱段视为了两端各有一个相切半球的胶囊体。由于测量机部件的各段之间一般都是首尾相连的，这种简化对测量点的可达性分析影响很小。

为了提高第3步中最小距离计算的效率，将坐标测量机和工件所在的三维空间分割成若干正方体分区，并确定每个空间分区中的三角面片。在计算测量机部件的球形段/圆柱段的球心/轴线段到三角面片的距离时，首先确定球形段/圆柱段所在的空间分区，然后计算球形段/圆柱段的球心/轴线段到所在空间分区中全部三角面片的距离。确定每个空间分区中的三角面片的方法为：若一个三角面片的包围盒与某个空间分区相交，则根据分离轴理论[14]进一步判断该三角面片是否与该空间分区相交，若相交则该三角面片属于该空间分区。分离轴理论指出：若存在一条轴线使得两个凸体在轴线上的投影不相交，那么这两个凸体不相交，这条轴线就是分离轴；若找不到分离轴，则两个凸体相交。如果两个凸体都是简单的规则几何体，那么判断二者是否相交仅需考虑有限的几个可能的分离轴，如果两个凸体在这些可能的分离轴上的投影都相交，那么这两个凸体相交。判断三角面片与正方体是否相交仅需考虑的分离轴有：正方体的3个法向量、三角面片的法向量、正方体互相垂直的3条边的方向矢量分别与三角面片的3条边的方向矢量的叉积。

3 动态可达性分析

假设测量方向d在静态可达性分析中被确定为测量点p的可达方向，那么在测量方向d下，测量点p未必是动态可达的，亦即：可能不存在一条路径，使得在探针以角度d的姿态从一个位置移动到触碰测量点p的过程中，坐标测量机的活动部件不与工件等障碍物发生碰撞。测量点p在测量方向d下的动态可达性分析涉及无干涉测量路径的搜寻，问题非常复杂。根据测量路径类型的不同，本文将动态可达性分析分为两个阶段进行。

坐标测量机在接触式点位测量模式下的测量路径如图4所示。探针首先从初始位置快速移动到测量点P1法线上方的预接近点A1，再沿着法线慢速探测测量点P1，之后回退到法线上方的回退点B1，然后快速经过避障点C移动到预接近点A2，再沿着法线慢速探测测量点P2，并回退到回退点B2……如此反复，逐点测量。预接近点到测量点之间的直线路径称为探测路径，其长度称为预接触距离；测量点到回退点之间的直线路径称为回退路径，其长度称为回退距离；其他路径统称为快速定位路径（图4中虚线所示）。预接触距离和回退距离是坐标测量机的测量参数，其设置完成之后，每个测量点的探测路径和回退路径也就完全确定下来了，而快速定位路径则在测量路径规划阶段确定。

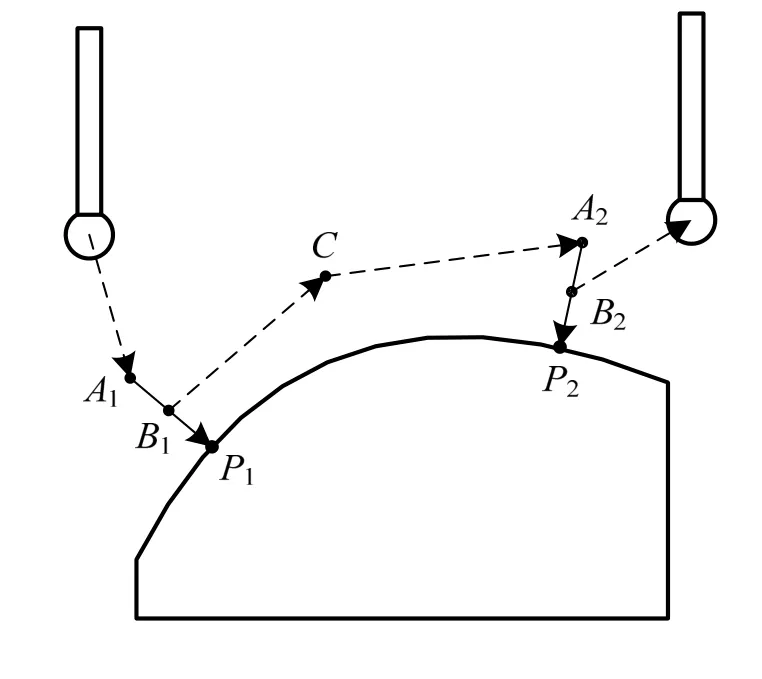
图4 测量路径

第1阶段的动态可达性分析在静态可达性分析之后，测量方向选择之前，用于分析探针以测量角度d的姿态沿着探测路径和回退路径移动的过程中测量机的活动部件是否与障碍物碰撞。这是因为，在探测路径和回退路径产生的碰撞只能通过更改测头的测量角度规避，如果在测量角度选择之后的测量路径规划阶段才发现在这两段路径上存在干涉，就必须重新选择测量角度并重新规划测量路径，检测规划效率比较低。由于探测路径和回退路径在测量路径规划之前就已经通过设置预接触距离和回退距离确定下来了，可以将探测路径和回退路径的干涉检查放在测量角度选择之前进行，从而避免重新选择测量角度和规划测量路径。第一阶段得到的测量点的动态可达方向用于测量方向的优化选择。

第2阶段的动态可达性分析在测量方向选择完成之后的测量路径规划阶段进行，首先确定测量点的测量顺序并规划初始的快速定位路径，然后分析在快速定位路径上测量机的活动部件是否与障碍物碰撞，若存在碰撞则采取设置避障点等措施规避碰撞。

探针在测量路径上的移动是连续的，干涉检查有两种办法：（1）分析测量机活动部件在沿着测量路径移动过程中形成的扫描体与障碍物是否存在干涉；（2）将测量路径进行等距采样，分析测量机活动部件在各个采样点处是否与障碍物存在干涉，采样间距越小，干涉检查越准确。由于有了静态可达性分析的基础，采用第2种办法进行干涉检查，亦即计算活动部件在各采样点处与障碍物之间的最小距离来判断是否存在干涉，方法与静态可达性分析的第3步完全一致。

4 应用实例

为了测试本文提出的测量点可达性分析方法的有效性，我们基于本文所述方法开发了一个原型系统。系统由测量设备库、设备库管理器、虚拟测量环境构建和可达性分析四个模块构成。测量设备库用于存储测量设备，包括测量机、测头、探针、夹具等等；设备库管理器用于测量设备库的管理，包括添加新的测量设备，删除、查询和修改测量设备等功能；虚拟测量环境构建模块用于调用测量设备，并完成测量设备的自动安装，以及工件和夹具的交互安装；可达性分析模块在虚拟测量环境中对工件上各个测量点的可达性进行自动分析，并输出每个测量点的可达方向。

图5所示为一个飞机结构件。该零件比较典型，具有孔、槽、型腔、型面等多种结构特征，而且为了减轻重量，还具有复杂的内腔结构，内腔里面的可达性较差。我们在该零件上多个具有代表性的位置处布置了若干测量点，既有位于零件表面的测量点，也有位于零件内腔的测量点。然后应用原型系统对使用不同类型探针测量各个测量点的可达性进行了分析。首先分析球探针测量各个测量点时的可达方向。探针测尖半径为2mm，探针测杆半径为1mm，探针长度为30mm，测头半径为7mm，测头长度为80mm。经过静态可达性分析和第一阶段的动态可达性分析，图6(a)中位于顶面的测量点1有1186个可达方向，图6(b)中位于孔壁的测量点2有124个可达方向，图6(c)中位于内腔里面的测量点3只有3个可达方向，测量点4没有可达方向，不可达。更换探针和测头，重新分析测量点4的可达性。探针测尖半径为1.5mm，探针测杆半径为1mm，探针长度为50mm，测头半径为7mm，测头长度为120mm。经过静态可达性分析和第一阶段的动态可达性分析，测量点4的可达方向如图7(a)所示，共有109个可达方向。图7(b)所示为用星形探针的周向测尖测量位于一个内腔顶部的测量点5时的可达方向，一共有148个可达方向。

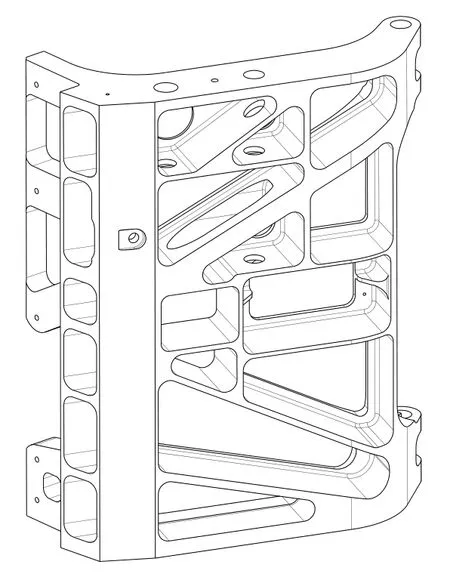
图5 飞机结构件

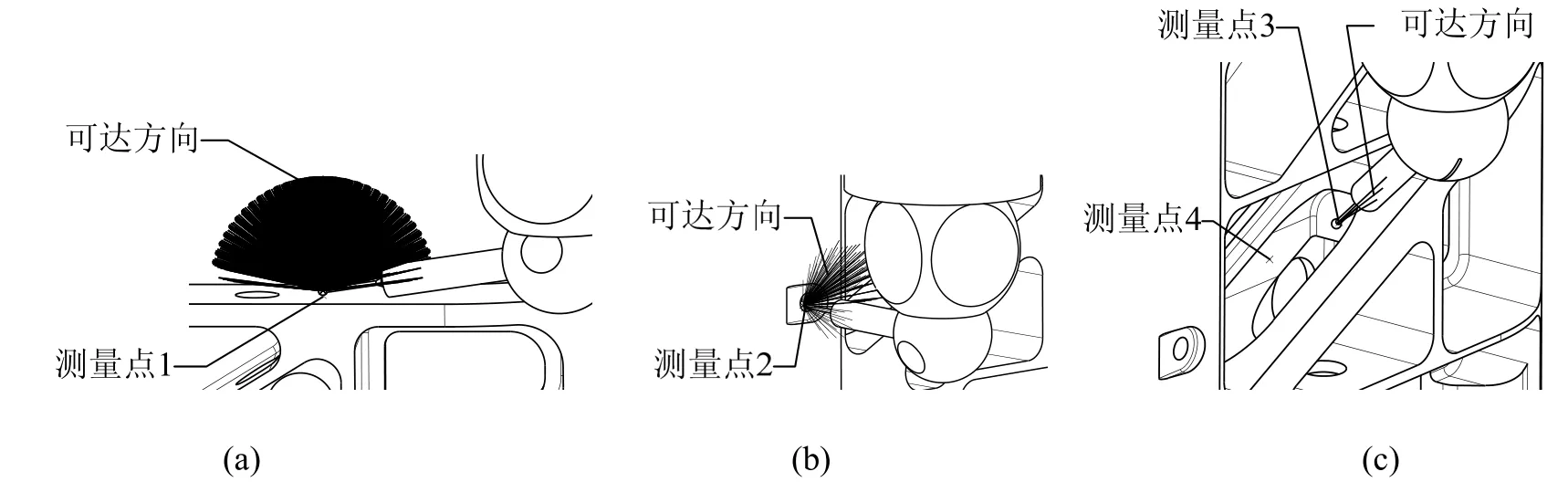
图6 短球探针可达方向

图7 3种探针可达方向

经过静态可达性分析和第1阶段的动态可达性分析得到了每个测量点的可达方向，在此基础上对测量方向进行了选择，并将测量点按照测量方向进行分组，同一组内的测量点的测量方向相同。然后采用模拟退火算法对测量点的顺序进行了优化，相邻测量点之间初始的快速定位路径设置为直线路径，之后分析在快速定位路径上测量机的活动部件是否与障碍物碰撞，若存在碰撞则采取设置避障点等措施规避碰撞。例如在图7(c)中，用球探针测量测量点3和测量点6所用的测量方向为图中测头正处于的测量方向，经过第2阶段的动态可达性分析，检查到探针在测量点3到测量点6的初始快速定位路径上与零件存在碰撞，设置A、B两个避障点，并再次进行动态可达性分析，探针在从测量点3到测量点6所经过的3条快速定位路径上与零件不存在碰撞。

5 结 论

本文针对常见类型的探针提出了一种通用的测量点可达性分析方法，支持对用户建立的任意的简化测量机部件模型用于测量时的可达性进行分析，精确地计算出测量点的全部可达方向，而且，既能进行静态可达性分析，也能进行动态可达性分析。由于在干涉检查中对零件进行了离散化处理，因此，该方法适用于任意类型和复杂程度的零件。试验结果表明，本文所提出的方法能够对测量点的可达性进行精确地分析。目前除了探针测尖外，该方法只支持用户通过圆球和圆柱两类基本几何体，建立其他测量机活动部件的模型。但是，这在实际应用中对可达性分析的影响很小，因为测量机活动部件多数是由圆球和圆柱体构成的，圆锥体和棱柱等其他几何体所占比例很小，而且圆锥体的锥角一般比较小，可以由球心在圆锥轴线上的多个不等直径的圆球或者同轴的多个不等直径的圆柱体近似，棱柱可以由最小包络圆柱体替代。建立模型的基本几何体以后需要扩充，增加圆锥和棱柱等几何体，以使测量点的可达性分析更加精确。

[1]Spyridi A J. Automatic generation of high level inspection plans for coordinate measuring machines [D].Los Angeles, USA: University of Southern California,1994: 15-94.

[2]Spyridi A J, Requicha A A G. Accessibility analysis for polyhedral objects [C]//Tzafestas S G. Engineering systems with intelligence. Dordrecht, Netherland:Kluwer Academic Publishers, 1992: 317-324.

[3]Spyridi A J, Requicha A A G. Accessibility analysis for the automatic inspection of mechanical parts by coordinate measuring machines [C]//1990 IEEE International Conference on Robotics and Automation.Cincinnati, USA: 1990: 1284-1289.

[4]Spitz S N, Requicha A A G. Accessibility analysis using computer graphics hardware [J]. IEEE Transactions on Visualization and Computer Graphics,2000, 6(3): 208-219.

[5]Spitz S N. Dimensional inspection planning for coordinate measuring machines [D]. Los Angeles,USA: University of Southern California, 1999: 9-32.

[6]Spitz S N, Spyridi A J, Requicha A G. Accessibility analysis for planning of dimensional inspection with coordinate measuring machines [J]. IEEE Transactions on Robotics and Automation, 1999, 15(4): 714-727.

[7]Limaiem A, Eimaraghy H A. Integrated accessibility analysis and measurement operations sequencing for CMMs [J]. Journal of Manufacturing Systems, 2000,19(2): 83-93.

[8]Limaiem A, Elmaraghy H E. A general method for analysing the accessibility of features using concentric spherical shells [J]. The International Journal of Advanced Manufacturing Technology, 1997, 13(2):101-108.

[9]Wu Yongqing, Liu Shugui, Zhang Guoxiong.Improvement of coordinate measuring machine probing accessibility [J]. Precision Engineering, 2004,28(1): 89-94.

[10]吴永清. 智能三坐标测量机检测规划中若干关键技术的研究[D]. 天津: 天津大学, 2001: 36-48.

[11]Chang Huichin, Lin Alan C. Five-axis automated measurement by coordinate measuring machine [J].The International Journal of Advanced Manufacturing Technology, 2011, 55(5): 657-673.

[12]Alvarez B J, Fernandez P, Rico J C, et al. Ray-tracing techniques applied to the accessibility analysis for the automatic contact and non contact inspection [C]//Ao S, Gelman L. Advances in Electrical Engineering and Computational Science, Lecture Notes in Electrical Engineering. Netherlands: Springer, 2009: 459-469.

[13]Alvarez B J, Fernandez P, Rico J C, et al.Accessibility analysis for the automatic contact and non-contact inspection on coordinate measuring machines [C]//Proceedings of the World Congress on Engineering 2008. London, U.K.: 2008: 117-122.

[14]Schneider P J, Eberly D H. Geometric tools for computer graphics [M]. San Francisco, USA: Morgan Kaufmann Publishers, 2003: 265-284.