转载点物料颗粒运动的数值模拟

朴香兰， 郭 越

（延边大学工学院，吉林 延吉 133002）

转送站固体颗粒物料的实际运动十分复杂，除受到输送带的速度、滚筒半径、输送机布置形式、物料与输送带的摩擦系数等影响外，还受到物料内部运动的影响。Rovertst A.W.[1]Wensrich C.M.[2]Maton A.E.[3]等分别从不同角度研究了物料颗粒的运动及边界的设计。周家海[4]、宋伟刚等[5]分别对带式输送机卸料时的物料运动轨迹做了研究，并用不同方法绘制了轨迹线。采用连续介质的力学方法，只能把散装物料颗粒群体作为一个整体来考虑，无法分析散粒群体中每个颗粒的运动过程、相互作用及其对整体运动的影响。本文利用基于离散元理论的颗粒流代码程序，建立了转送站物料运动的离散元模型，在此基础上研究了散料颗粒的运动过程、相互作用及其挡板对颗粒流能量损耗的影响，并模拟了卸料的整个过程，最后得出结论。

1 离散单元法（DEM）简介

离散单元法（Discrete Element Method，简称DEM）是把不连续体分离为刚性元素的集合，使各个刚性元素满足运动方程，用时步迭代的方法求解各刚性元素的运动方程，继而求得不连续体的整体运动形态。

离散元法与连续介质力学方法相比有本质上的不同。它根据离散体的离散特性来建立数值模型，因此更符合离散物质本身的性质，在分析具有离散性质的物质材料方面表现出了极大的优越性。使用离散元法对颗粒材料进行模拟分析，可以直接获得大量离散物质的复杂行为信息，从而可以进一步假定和分析离散物质的细观结构，为准确预测和分析现有连续介质理论无法解释和分析的物质力学行为提供了可行的途径。

离散元法不需要过多的假设，使用简单的方程就可以对高度复杂系统的准静态和动态行为进行模拟。离散单元法的原理较为简单，只需要满足两组基本方程：第一是运动方程（牛顿第二运动定律）；第二是物理方程（力—位移关系）。方程采用中心差分公式进行动态求解[6]。

目前有二维、三维粘弹性接触模型、Hertz理论接触模型、填隙流体的湿颗粒作用模型等[7]。本文采用Hertz理论接触模型。

2 数值模拟及结果分析

2.1 转送站离散元模型的建立[8]

以PFC3D为平台，采用基本单元为球形颗粒，在限定范围内随机生成1000个物料颗粒，颗粒半径在25～35mm之间。滚筒的模型是采用一个圆柱面和两个有向面来构成，如图1所示。生成的每个颗粒在重力加速度下降落到带子上方，达到初始平衡状态，如图2所示。

图1 滚筒离散元模型

图2 初始平衡状态

2.2 参数设定

设定仿真所需的一些参数，如几何特性、材料属性、摩擦系数、阻尼系数等，如表1所示。

表1 模拟参数

2.3 数值模拟与分析

2.3.1 卸料轨迹的模拟

采用带速为3m/s，当运行一定时步后，卸料过程仿真状态如图3所示。图中黄颜色表示颗粒间、颗粒与边界间的相互作用力场。当滚筒前设有一与料流方向成90°的挡板时，模拟物料的运动轨迹如图4所示。通过理论计算绘制的轨迹线如图5所示[9]。由图3可见，在滚筒圆的水平轴线方向上，即z=0的方向上，物料中心的轨迹离滚筒中心的距离约等于1m，这与图5物料中心轨迹线基本相符。这说明仿真时设定的参数基本正确、模拟可信。

图3 物料的卸料过程仿真

图4 设有挡板的料流模拟

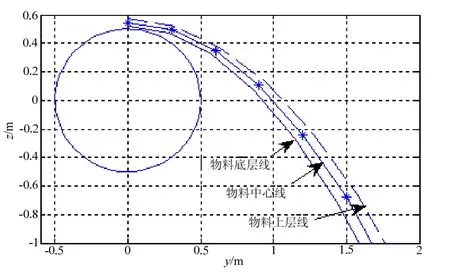
图5 物料不同层的轨迹线

2.3.2 不同的运行速度对颗粒之间相互作用的影响

颗粒之间的相互作用可通过平均接触力和平均不平衡力来描述。平均接触力是指颗粒与颗粒之间以及颗粒与边界之间的接触力在运行时步范围内的平均值，而平均不平衡力是指颗粒所受外加作用力未达到平衡时的平均值。

取带速分别为3m/s、4m/s和5m/s时，平均接触力和平均不平衡力分别如图6所示。图中纵坐标表示平均接触力（红线）及平均不平衡力（黑线）。共同的时步范围是6.005×104～1×105s。从模拟数据可知，当颗粒速度增加时，平均接触力的最小值基本一致，平均接触力的最大值随颗粒速度的增加而增加。但平均不平衡力无论是最大值、最小值随速度的变化不大。

2.3.3 不同运行速度对能量消耗的影响

不同颗粒运行速度时的能量历程如图7，纵坐标表示各种能量值。与图7对应的能量界限值如表2。从图7及表2可见：能量变化最明显的是动能（黑线），其次是实体能（红线）、摩擦能（深蓝线）、应变能（绿色）和边界能（天蓝色）。动能计入所有粒子的平移及旋转运动，实体能是由全部体力作用在集合粒子上而积聚的能量。全部体力包括重力荷载以及所有外加作用力和力矩。边界能是由所有边界(wall)作用在集合粒子上而积聚的能量。随着颗粒速度的增加，其动能急剧增加，而边界能的变化很缓慢。这是因为动能与颗粒速度的平方成正比。但对边界能来讲，由于速度的增加，边界对颗粒的作用几率相对于颗粒之间的作用几率反而减少，因此边界能的变化很缓慢。

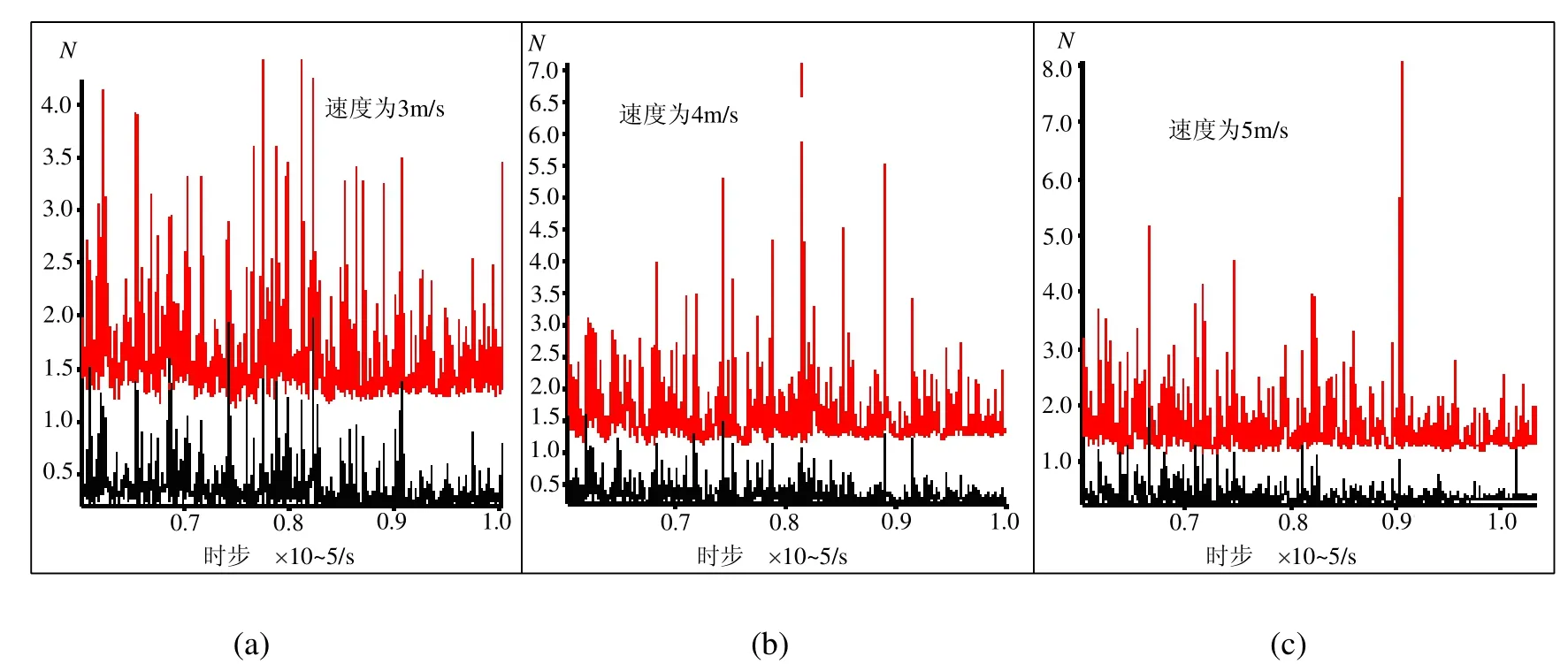
图6 平均接触力和平均不平衡力

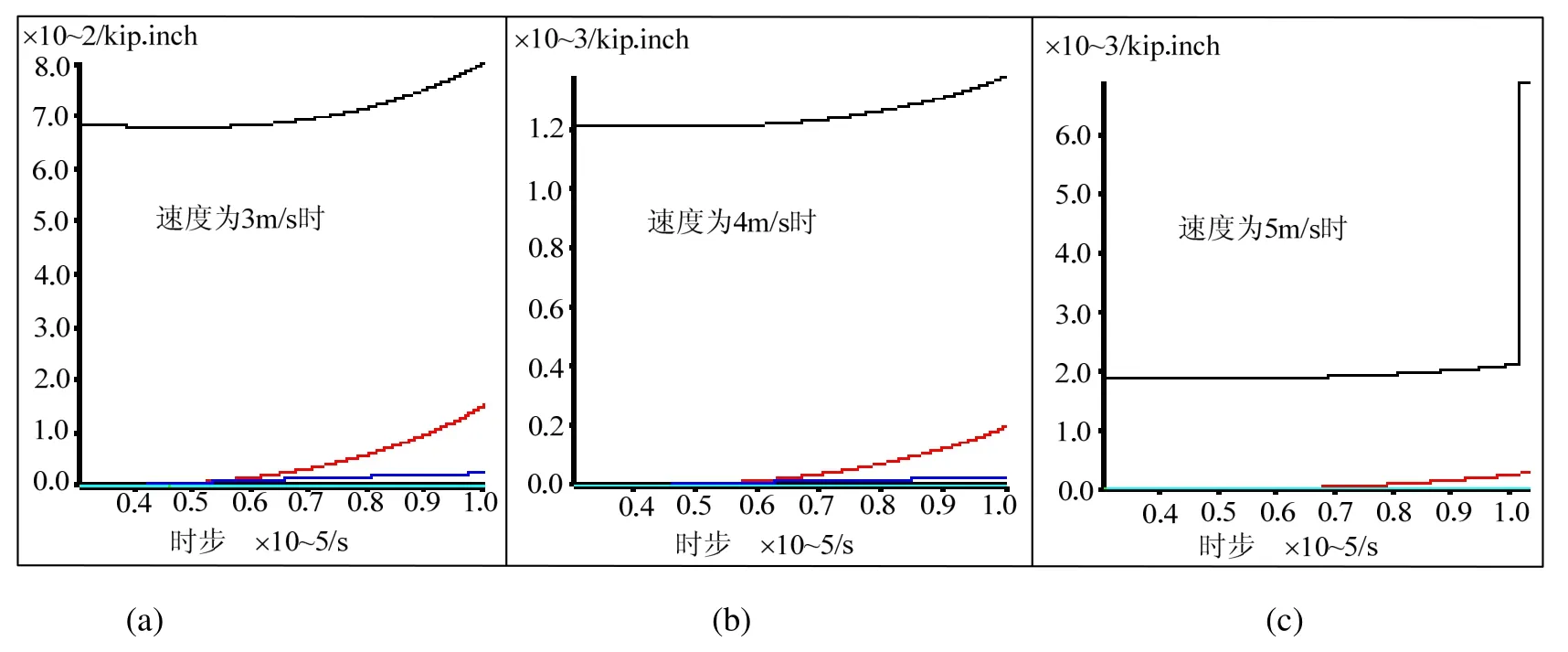
图7 能量历程

表2 能量界限值

2.3.4 任意颗粒在给定方向的速度及位置的变化

当颗粒速度分别是υ=3、4、5m/s时，对应的纵向速度（黑线）及纵向位移（红线）如图8所示。图中纵坐标表示速度及位移(m)。任选质心坐标为（0，0，0.5）的颗粒，对应3种颗粒速度的颗粒ID分别为901、929、678。图8(a)纵向位移在给定的时步（6.005×104～1.003×105）内由0.5281m降到0.3018m；图8(b)纵向位移在相同时步内由0.5252m降到0.2736m；图8(c)纵向位移由0.5274m降到0.3851m。说明纵向位移随颗粒速度的改变不大。而速度在给定的时步内，虽然速度变化趋势大致相同，但随颗粒速度的变化，纵向速度的波动也越来越大。这是颗粒速度的增加，使得颗粒之间、颗粒与滚筒前挡板碰撞机会增加的缘故。

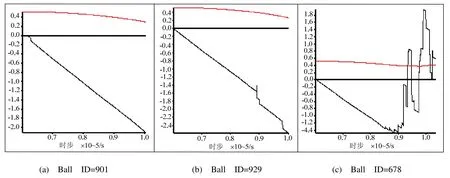
图8 颗粒的速度、位移变化

2.3.5 挡板对能量消耗的影响

在输送机头部滚筒前离轴线1m处，设置与料流方向成90°的挡板后对能量历程进行跟踪，其能量变化如表3。与图7及对应的能量界限值表2进行对比可知，有挡板时动能的变化是随着速度的增加急剧上升，尤其是动能的最大值变化很大；其次是应变能和摩擦能，实体能和边界能几乎没有变化。

3 结 论

对转载点物料颗粒运动进行数值模拟可知，平均接触力最小值随速度的变化不大，平均接触力的最大值随着速度的增加而增加。但平均不平衡力的最大值、最小值随速度的增加变化很小。任意颗粒的垂直速度随着速度的增加出现波动现象。通过能量历程的跟踪观察实体能、边界能、摩擦能、动能、应变能等的变化，发现颗粒速度的增加将导致颗粒运动动能的急剧增加，其次是实体能，摩擦能、应变能和边界能。加了挡板之后能耗的增加主要体现在动能、应变能和摩擦能的变化。

基于PFC3D的转载点物料颗粒运动的数值模拟，能直观地展现料流的宏观运动，可获得物理实验所不能取得的信息，如物料颗粒运动的力场、速度场，可以实时追踪所有变量并能存储起来，如能量历程的跟踪等，还能考察单个颗粒的运动形态。

[1]Roberts A W. Chute performance and design for rapid flow conditions [J]. Chemical Engineering and Technology, 2003, 26(2): 163-170.

[2]Wensrich C M. Evolutionary optimization in chute design [J]. Powder Technology, 2003, 138: 118-123.

[3]Maton A E, Transfer Station Design [J]. Bulk Solids handling, 2009, 29(1): 30-34.

[4]周家海, 王卫利, 王军浩, 等. 带式输送机的卸料轨迹研究[J]. 水运科学研究, 2007, (2): 5-9.

[5]宋伟刚, 周先莲, 张明远. 带式输送机卸载过程中物料轨迹的计算方法[J]. 矿山机械, 2000, 8: 41-43.

[6]黄晚清, 陆 阳, 何昌轩, 等. 球体颗粒随机堆积的三维动态模拟[C]//可持续发展的中国交通——交通运输工程学科(下册), 2005: 1454-1458.

[7]解本铭, 朱 晨, 崔大妍. 散装物料流动特性及仓体设计研究进展[J]. 煤矿机械, 2005, (12): 3-5.

[8]Katterfeld A, Groger T, Minkin A. Discrete element simulation of transfer stations and their verification [J].Bulk solids & Powder, 2007, 2(2): 137-143.

[9]朴香兰, 郭 越. 卸载过程的物料运动研究[J]. 工程图学学报, 2010, 31(4): 12-16.