大规模点云选择及精简

范 然， 金小刚

（浙江大学CAD&CG国家重点实验室，浙江 杭州 310058）

逆向工程中最普遍的应用模式是利用基于光学原理的扫描设备测量零件或模具外表面形成点云数据，从中提取几何特征进而重建多边形或 NURBS曲面[1]。随着扫描硬件精度的提升，原始扫描数据能够较好逼近物理模型的曲面形态，但是，删减处理始终是不可或缺的关键步骤。根据被测物体的摆放方式，扫描点云中不可避免地包含如墙面、支撑物等非目标背景数据，解决这一问题需设计能够高效并灵活指定大规模点云中待删除区域的选择算法。此外，原始扫描点云通常由多次测量的单片数据拼合而成，接合处存在重叠冗余采样，而且数据规模大、分布不均匀，普通计算机的计算及内存资源不易直接对其进行曲面重建。针对这一问题，点云精简算法的目标是减少数据量并使采样点依几何特征自适应均衡分布。

由于常用计算机输入方式是二维指针设备，二维套索UI是点云选择最直观的交互方式。研究领域通常使用简单空间形体实现点云选择[2]，并未给出支持套索UI的点云选择算法。目前，在逆向工程应用领域中多使用Geomagic[3]、Rapidform[4]等商业软件进行处理，相关算法并未公开，无法满足研究领域构建低成本三维扫描系统的需求。因此本文提出了一种支持套索UI的大规模点云选择算法，利用套索形状的矩形覆盖与输入点云八叉树编码剔除大部分点在多边形内判断。不同于传统的平面射线奇偶法及其改进算法，本文方法利用了扫描点云密集分布的特点，能够整体判断点云的局部区域。

点云精简通常有两种定义[5]：给定容许误差阈值计算最小采样数分布；给定目标采样点数目搜索最小误差分布。在逆向工程中后者相对合理，用户通常希望点云精简算法同时具备如下特性：1）任意指定目标采样点数目；2）不改变原有采样点位置以维持扫描精度；3）尽可能保留尖锐几何特征，依曲面曲率自适应均衡分布。然而，传统基于曲率自适应[6]以及基于QEM误差[7]的点云精简方法具有采样点局部聚集以及不能保持尖锐边特征与边界的缺点。本文利用Poisson-disk采样原理获得简化后点云均衡分布的效果，并以采样点邻域球布尔交运算来定义曲面上的圆盘半径度量、扩展采样边界，获得了尖锐边特征及边界保持的性质。

1 相关工作

点云选择算法涉及如何判断采样点在视平面上的投影与套索多边形之间的包含关系。Eric[8]总结了若干经典的点在多边形内测试方法，包括射线奇偶、角度和、三角形扇等算法。在地理信息与图形学领域，目标应用通常需实时测试大规模数据，经典方法无法满足速度指标，后续研究采用基于区域分解的分治策略进行优化。Li[9]等分解多边形为凸子域，将点在任意多边形内测试转换为更为简单的点在凸多边形内测试。Zalik[10]等将多边形所在区域分解为均匀单元格并赋予内、外、边界属性，首先进行简单的点在单元格内测试，最后仅对包含于边界单元格的点执行完整测试。Yang[11]等利用近似最近点概念提高了均匀单元格方法的准确度。本文注意到现存方法仅注重分解或降低多边形复杂性然后进行逐个单点测试，针对大规模扫描点云数据密集分布的特点，将输入点云组织为八叉树层次结构，以局部区域为单元判断包含关系，剔除大部分点在多边形内测试。

随着基于点的绘制与造型技术的发展，已经存在许多算法简化点云数据。根据精简点云采样分布形成的方式可将现有方法分为3类：迭代最优剔除、层次聚类、曲面重采样。不同的方法分别侧重减少原始点云与精简后点云之间的距离、曲率自适应、分布质量等方面。迭代最优剔除方法的优点在于采样前后的点云距离误差小，缺点在于随着点云规模的增加由于全局排序、属性更新需要大量的内存与计算消耗，不适合逆向工程中海量点云高效精简，且不容易保留尖锐边特征与边界。Pauly[7]等将三角网格的QEM简化算法推广到点云上。Linden[12]提出一种综合的采样点影响度，每次移除最小影响度的采样点。Song[13]等首先识别出尖锐特征采样点并予以保留，其余采样点依次按照影响度排序迭代去除。层次聚类方法具有计算效率高的优点，其缺点是不容易控制采样点的分布与误差。Lee[6]等采用非均匀八叉树对点云进行聚类并以法向变动控制八叉树细分，效率较高，但精简点云分布不均匀。Yu[14]等利用k-means算法对点云进行层次分割，采用局部协方差分析控制聚类过程，虽然分布质量提高但无法精确指定采样点数目。Shi[15]等同样利用k-means算法获得了类似的效果。Song[16]等采用全局聚类方法具有更加优良的分布效果，但由于其全局优化特性计算效率较低。现有的曲面重采样方法直接从分布特性角度出发，能够获得理论上最优采样点分布，但由于通常需计算流形上的距离或维持采样点之间的动态平衡，其所消耗的计算资源也是最大的。Moenning[17]等利用Fast Marching方法渐进计算内蕴Voronoi图以实现最远点采样策略。Pauly[7]等人将粒子平衡模拟方法推广到点云上。

上述3类方法分别体现了优化、数据分析、几何结构分析的思想，本文的点云精简方法属于曲面重采样，基于Poisson-disk采样均匀分布采样点、防止过度集中，利用邻域球布尔交运算扩展可用采样边界，如图9和图10所示由于尖锐边特征以及边界数据不容易被周围邻域球覆盖从而被密集采样。与本文目标最接近的方法是Kang[18]等提出的均衡点云采样方法，不同之处在于基于Poisson-disk采样的方法能够通过采样半径调整点云分布。

2 支持套索UI的大规模点云选择算法

点云选择的套索UI接口与图像区域选择类似，用户旋转点云模型至合适方位后草绘套索多边形、圈选目标区域，如图1(a)和图1(b)所示，遴选出投影在套索多边形之内的点云区域。最基本的实现方式是将每个采样点投影在视平面上逐个进行点在多边形内测试，然而对于百万级甚至千万级的扫描点云数据，该方法无法获得理想的交互性能。

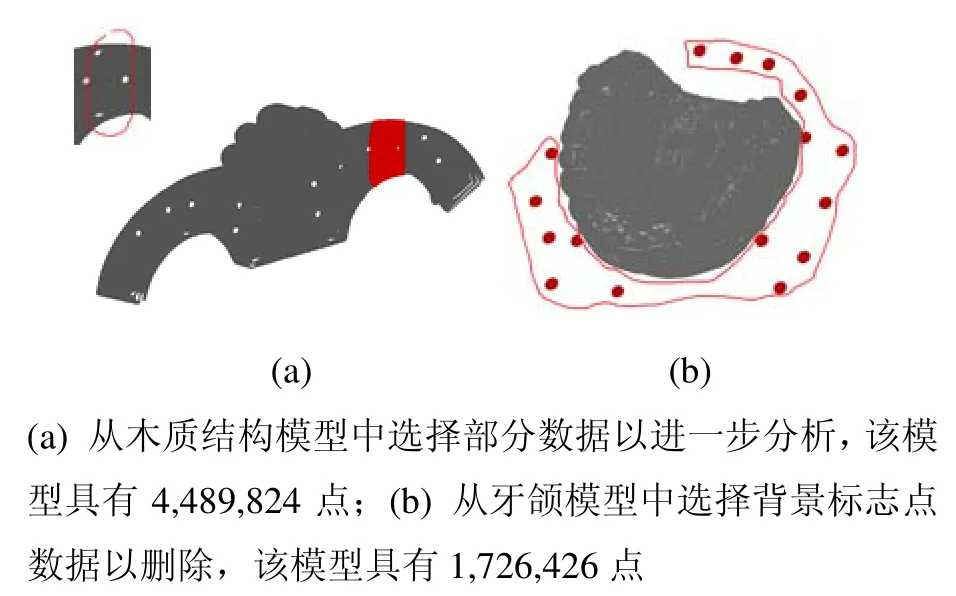
图1 套索UI点云选择

本文算法受到Zalik[10]等方法的启发，该方法主要针对地理信息应用，不适合直接用于选择扫描点云数据。首先，该方法只能处理简单曲线，在点云区域选择中，限制用户输入的套索形状为简单曲线并不合理。本文提出的算法构造了输入多边形的矩形区域覆盖并利用改进的射线奇偶法赋予内、外、边界属性，图2比较了Zalik[10]等方法与本文方法处理非简单曲线的差异。

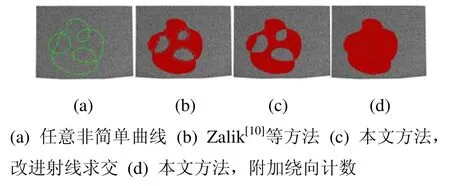
图2 输入非简单曲线，从纸张点云模型中选择数据

此外，本文注意到扫描点云数据通常是密集分布的，因此，将原始点云嵌入八叉树层次结构，利用节点单元在视平面上投影与矩形覆盖之间的几何包含关系剔除大部分点在多边形内测试。

2.1 套索多边形矩形覆盖

给定多边形P，由边列表{E1,E2,… ,En}构成，其中Ei连接顶点(xi,yi)和 (xi+1,yi+1)。设C为任意矩形，定义P的矩形覆盖为{Ci}，要求矩形之间无交集且所有矩形的并集覆盖了P所在区域，即：DC(P) = {Ci|∪iCi⊃Pand ∀i≠jCi∩Cj=∅}。本文利用四叉树计算DC(P)，主要有两个优点：能够根据多边形P的距离场自适应确定矩形数量；索引矩形计算量较小。设c为四叉树节点单元，其位置由坐标函数x0(c),x1(c),y0(c),y1(c)确定，点(x,y)∈c：x0(c) ≤x＜x1(c)与y0(c) ≤y＜y1(c)。DC(P)由四叉树的所有末端子节点构成。根据与P的相对几何位置分别赋予矩形单元内部、外部、边界属性，其中边界属性是指P穿越该矩形，此外矩形单元的大小取决于相对于P的距离，即远离P的矩形较大，边界矩形较小。DC(P)由递归分裂四叉树节点构建而成，根节点是覆盖P的正方形。节点分裂由以下形状误差决定：

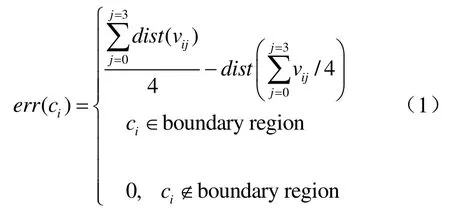
其中ci是四叉树节点，vij是其四个顶点之一，dist(vij)表示到P的距离函数。由于距离函数在P内部中轴附近存在一阶不连续使得线性逼近误差较大、节点分裂过多，为减少包含测试计算量通常需以尽可能少的矩形分别覆盖P的内、外、边界区域。因此(1)中显式地判断了ci是否具有边界属性。DC(P)的复杂性取决于P以及分裂阈值Te，该阈值由用户指定或者根据P的最小线段长度即P的分辨率确定，当err(ci)＞Te时分裂ci为4个子节点。

计算上述矩形覆盖需判断ic是否具有边界属性，如果P是凸多边形则可以通过对ic四个顶点执行点在多边形内测试得知其是否具有边界属性。对于一般的多边形，如果ic的4条边与P没有交点，根据连续性推断P没有穿越ic即不具有边界属性。本文采用结合单元边交点侦测的射线奇偶算法判断单元的内、外、边界属性，如图3所示该方法能够正确地赋予边界属性。

对于ci的每个顶点分别发射水平与竖直方向且与ci的边部分重合的射线，统计射线与P的交点数目并侦测交点是否落在ci的边上。以从ci的左上角顶点 (x0(ci),y1(ci))发射水平射线rright为例，对于所有Ej∈P，判断与rright的穿射关系。

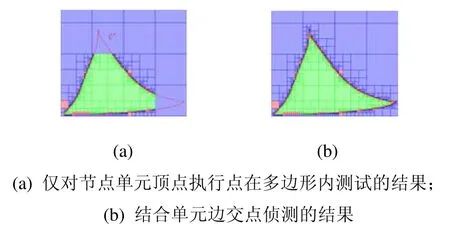
图3 基于四叉树的矩形覆盖，蓝色、绿色、红色分别表示外部、内部、边界属性

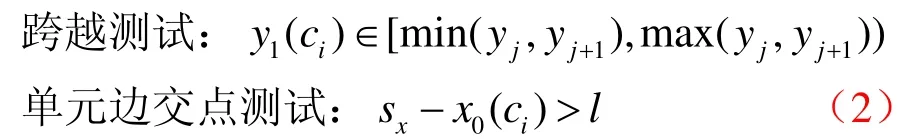
在DC(P)计算完成后，为了在后续测试中减少可能的求交运算，将组成P的所有线段嵌入矩形单元中。本文采用Lastra[19]等的射线穿透四叉树访问算法。设iE∈P，以t为参数可表示为：

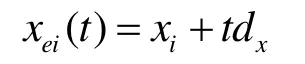
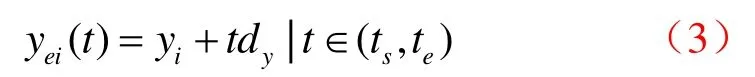
其中(dx,dy)是单位方向向量。首先确定包含起始顶点(xi,yi)的末端节点cs，移除包含在cs中的Ei部分、更新ts，同时将Ei记录在cs中；对于cs的父节点cp计算其4条边所在直线与Ei方向射线r的交点参数：

并按照下式断定Ei是否穿透cp：

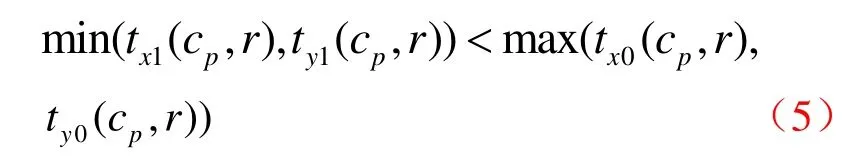
对于满足式(5)的cp，考察其所有子节点并移除Ej中被包含的部分，交替进行以上两步直至到达终止顶点 (xi+1,yi+1)。

2.2 点在多边形内测试

扫描点云具有密集分布的特点，可利用其空间一致性剔除大部分点在多边形内测试。本文将点云嵌入在八叉树G内，每个末端子节点不超过64个采样点。从根节点开始，将节点立方体gi∈G沿视线方向投影为侧影轮廓多边形gi′，其边界由同时邻接可见面与不可见面的立方体边投影而成，可见性由面法向与视线向量内积确定。判断gi′与DC(P)矩形之间的几何包含关系，分3种情况处理：

1）gi′包含在单个非边界矩形内的，将gi内所有采样点标识为与该矩形同样的属性；

2）gi′的所有顶点皆落在内部或者外部区域，侦测gi′的边与P的交点，采用Feito[20]等方法，无需计算出交点，并且已将P的边嵌入在DC(P)中因此只需做局部判断，如果没有交点将gi内所有采样点标识为gi′所在区域的属性；

3）gi′与具有边界属性的矩形有交集，递归处理gi′的子节点；

如果仍有末端节点gi′具有边界属性，将gi内的采样点投影在视平面上，如果落于具有内、外属性的矩形内，则赋予同样的属性。最后对落于边界矩形内的采样点执行基于射线奇偶的点在多边形内测试。经过上述层次测试步骤只有很少的一部分采样点需执行完整的点在多边形内测试，因而能够提升大规模点云区域选择的效率。

带预处理阶段的包含测试策略其核心在于将针对复杂多边形的测试转化为针对一组简单多边形的测试，这一策略有利于快速判断大量采样点针对同一多边形的位置。不同于之前的工作，本文基于点云密集分布、具有空间一致性的特性，将点云组织为八叉树结构，利用投影八叉树节点单元与多边形矩形覆盖之间的包含关系剔除了大部分点在多边形内测试。

3 基于Possion-disk采样的点云精简

在点云精简过程中显式地控制采样点分布对于尖锐边特征保持、边界保持、平坦与弯曲区域之间的均衡分布至关重要。其他基于减少简化前后点云间距离、曲率自适应的精简方法通常会造成采样点局部聚集、且不能密集采样尖锐边特征以及边界数据。后续应用如三角化、基于点的绘制、形状约束动画等的效果非常依赖于点云数据的分布质量。本文首先估计采样点法向，进而利用Poisson-disk采样控制采用点的分布，但由于Poisson-disk采样的控制参数是采样半径因而不容易控制采样点数目，本文对初步采样结果依采样点Voronoi邻域面积进行排序，向稀疏区域添加以及从拥挤区域移除采样点以达到目标精简数目。

3.1 法向估计

原始点云来源于不同的扫描技术，可分为带有法向与缺失法向两种情况。对于不具备法向信息的数据本文采用Pauly[7]等的方法，对每一个采样点pi利用局部协方差分析计算其法向ni，pi邻域的协方差矩阵为：

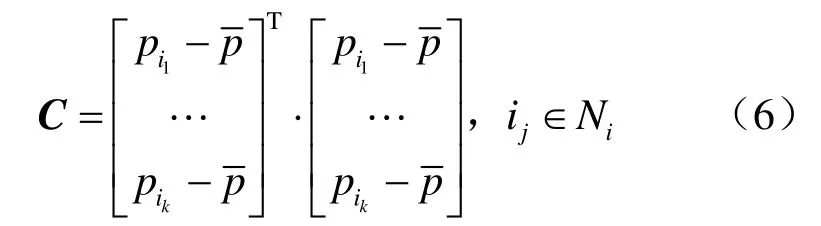
其中Ni是采样点pi的邻域，包括k个最近采样点，是位置均值。然后进行特征值分解并以其最小特征值向量作为该点的法向：

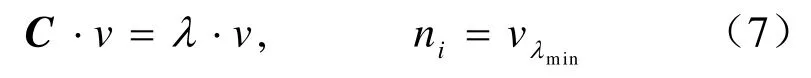
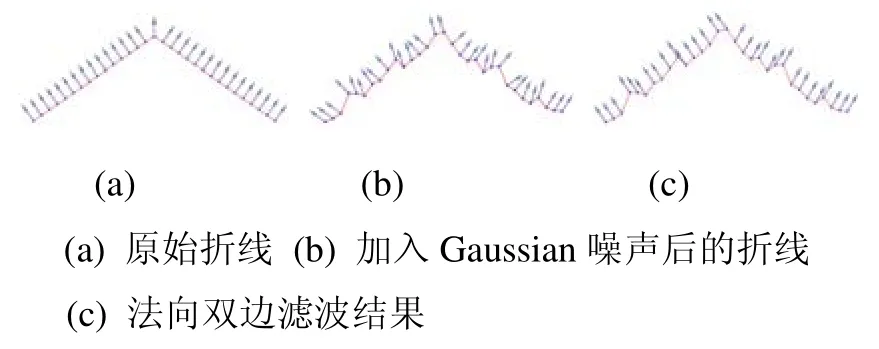
图4 法向双边滤波

需要指出的是本文算法并不需要统一法向定向，法向仅用于确定采样点的切平面。采用式(7)计算的法向对于光滑点云数据能够较好地逼近被测曲面法向，但不能良好表示逆向工程中常见的具有尖锐边特征的机械模型，而且增加采样分辨率并不能解决这一问题[21]。因此，本文采用法向双边滤波[22]，使得尖锐边特征两侧法向数据分区域平滑：

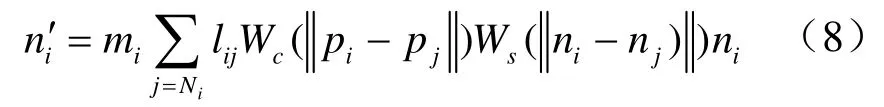
3.2 点云Possion-disk采样

Poisson-disk采样具有两种性质，即采样点符合随机分布、采样点之间的距离不小于2r，其中r是每个采样点所属圆盘的半径。飞镖投掷算法是最直接的生成方法，即随机生成新的采样点并判断该点所属圆盘是否被已经存在的采样点圆盘覆盖。投掷成功率随着采样点的增加而降低因而算法效率较低。Dunbar[23]等提出了基于边界区域增长的平面Poisson-disk采样算法，如图5所示，采样点及其所属圆盘用红色表示，可用采样边界用蓝色表示，初始3个采样点增长为6个采样点。采样过程主要包括两步：在可用边界上随机采样、更新可用采样边界。

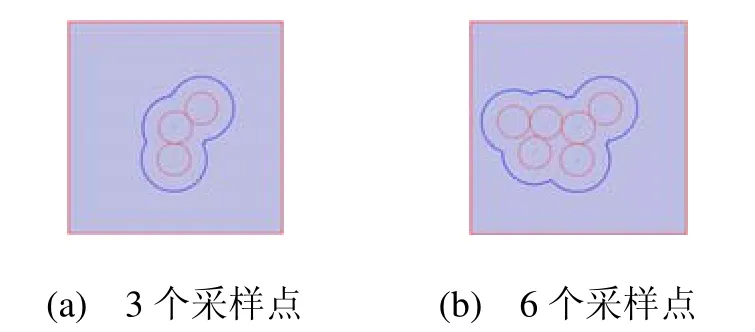
图5 平面Poisson-disk采样，蓝色表示可用采样边界

在曲面上进行Poisson-disk采样需定义适合的距离度量以确定每个采样点的影响域，Fu[24]等将Dunbar[23]的方法推广到三角网格曲面上，利用测地距离计算网格曲面上的等距线从而扩展采样边界。但是对于扫描点云数据，拓扑信息缺失、分布不均匀使得很难直接在点云上计算测地距离。本文的关键想法是基于Klein[25]等提出定义点云曲面的球影响图方法，对采样点ip定义半径为2r的邻域球Bi，所有采样点邻域球的集合构成对点云曲面的覆盖，将可用采样边界定义在采样点切平面与邻域球的交集上，可用采样边界的扩展通过邻域球布尔交运算实现。如图6所示，在加入新的采样点后，Bi内可用采样边界消去了邻域球Bj沿法向投影覆盖的部分。

采样边界更新后，从当前所有采样点邻域球内可用采样边界的集合中随机选取点p′，然后查找p′在点云中的最近点作为下一个采样点。其中，对每个已有采样点的采样边界赋予一概率值iq，随长度减少以及采样次数增加而减少。

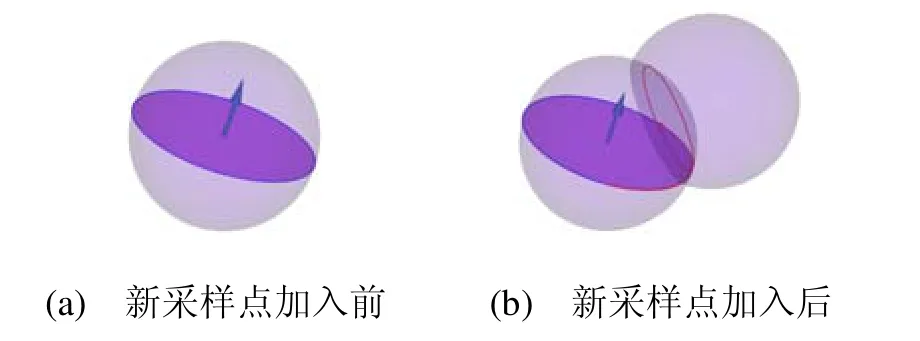
图6 邻域球布尔交运算，可用采样边界用蓝色表示，被消去的采样边界用红色表示

本文算法同样可用于点云重采样，只需将最近点查找替换为移动最小二乘点云曲面投影计算即可。算法主要计算量在于邻域球布尔交运算以及搜索最近点。采样半径r根据原始点云的的近似面积S按照下式计算[24]：

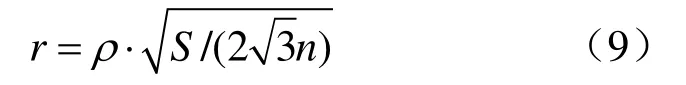
其中n是目标精简数目，ρ是疏密控制参数一般取为0.7，S根据原始点云的球影响图计算[25]。点云Poisson-disk采样算法步骤如下：

Step 1根据原始点云近似面积估计采样半径，随机选择一个初始采样点，生成初始可用采样边界。

Step 2根据每段可用采样边界的概率值，随机选取新的备选点，查找该点在点云中的最近点作为新的采样点。

Step 3利用邻域球布尔交运算更新可用采样边界，降低当前更新的可用采样边界段的概率值。

Step 4迭代2，3步直到所有邻域球内采样边界段最大概率值低于预先指定值Qτ。

初步采样结果接近预先指定的采样点数目，但由于Poisson-disk采样的控制参数是采样半径因而不容易精确达到该数目，本文对初步采样结果依采样点Voronoi邻域面积进行排序，迭代向稀疏区域添加或者从拥挤区域移除采样点以达到目标精简数目。

Poisson-disk采样保证了相邻采样点之间的距离不小于2r从而防止了在高曲率区域产生局部聚集以及在平坦区域均衡分布。同时，如图6所示，可用采样边界的更新依赖于邻域球的交集在曲面切平面内的投影，因此，在尖锐特征附近，由于法向差异较大导致相对密集的采样。

4 讨论与比较

本文的实验平台是Intel®Core™2双核处理器，1.86GHz，2G内存，NVIDIA GTS450显卡，Windows XP™操作系统。

图7显示了点云选择算法性能测试的真实扫描样例数据，如图8所示本文算法的速度快于射线奇偶法，对于规模较大的数据效果更加明显。同时本文与商业软件Geomagic[3]的点云选择功能进行了比较，获得了接近的用户体验。表1显示了本文点云选择算法的具体统计数据，主要包括矩形覆盖计算时间、内外判断时间以及单点包含测试剔除率。通过实验可以看出，主要计算时间消耗在构建矩形覆盖阶段；采样点数目与多边形复杂性共同决定了计算时间，例如图7(d)的时间消耗大于图7(e)；大部分点在多边形内测试被剔除，因而大大提升了交互速度。

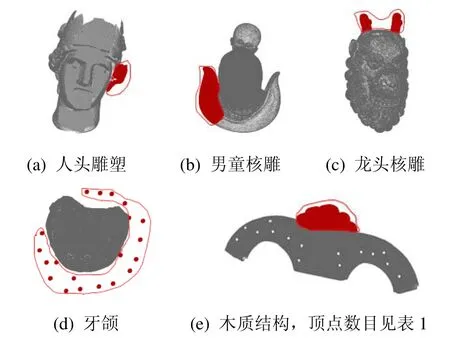
图7 点云选择算法测试例子

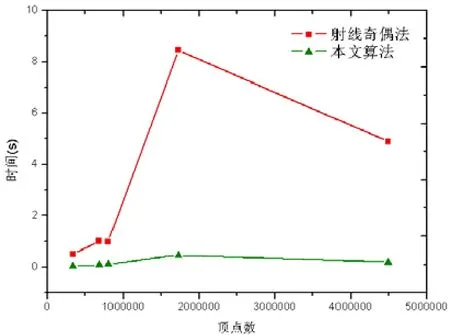
图8 点云选择算法速度比较

如图8所示，速度曲线图中数据依顶点增长顺序分别对应图7中的(a)、(b)、(c)、(d)、(e)。红色曲线表示射奇偶法，绿色曲线表示本文方法

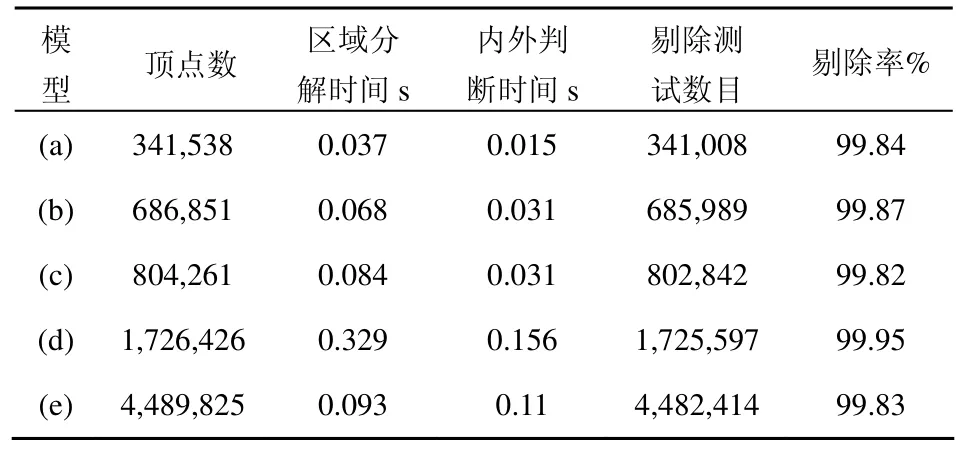
表1 点云选择算法统计数据表

本文与经典的曲率栅格以及均匀栅格[6]点云精简方法进行了比较。首先为了测试对尖锐边特征与边界的保持，针对立方体模型以及纸张模型进行了实验，其中立方体点云是由计算机生成的，纸张点云是真实的单幅扫描数据。如图9与图10所示，相较于曲率栅格与均匀栅格方法，本文算法加强了对尖锐边特征以及边界数据的采样，并在平坦区域均衡分布采样点。

图11显示了对真实扫描数据进行精简的例子，结果表明本文的方法在保持尖锐边特征与边界数据的同时防止了采样点局部聚集，获得了更加均衡的分布，因而更加有利于高质量三角化，基于点的绘制以及形状约束动画[26]。

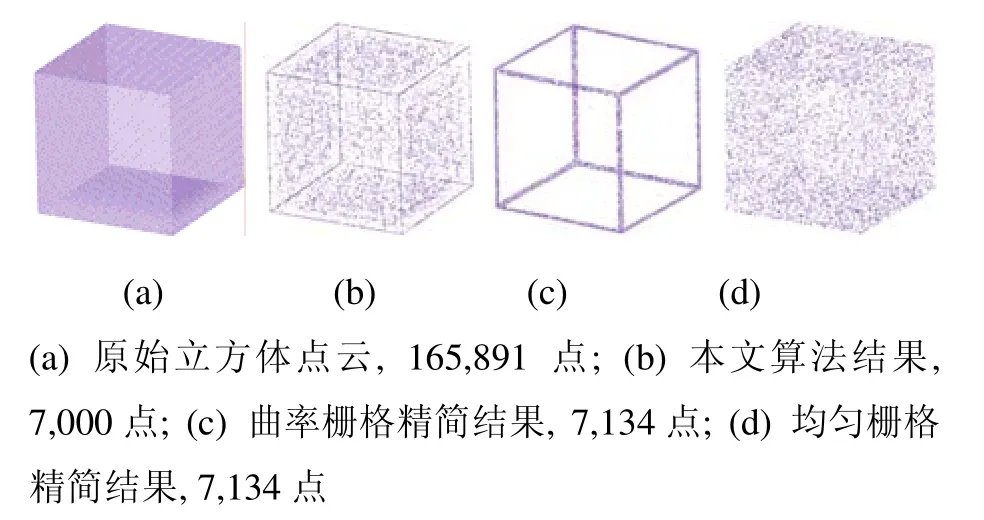
图9 立方体模型点云精简

图10 纸张模型点云精简

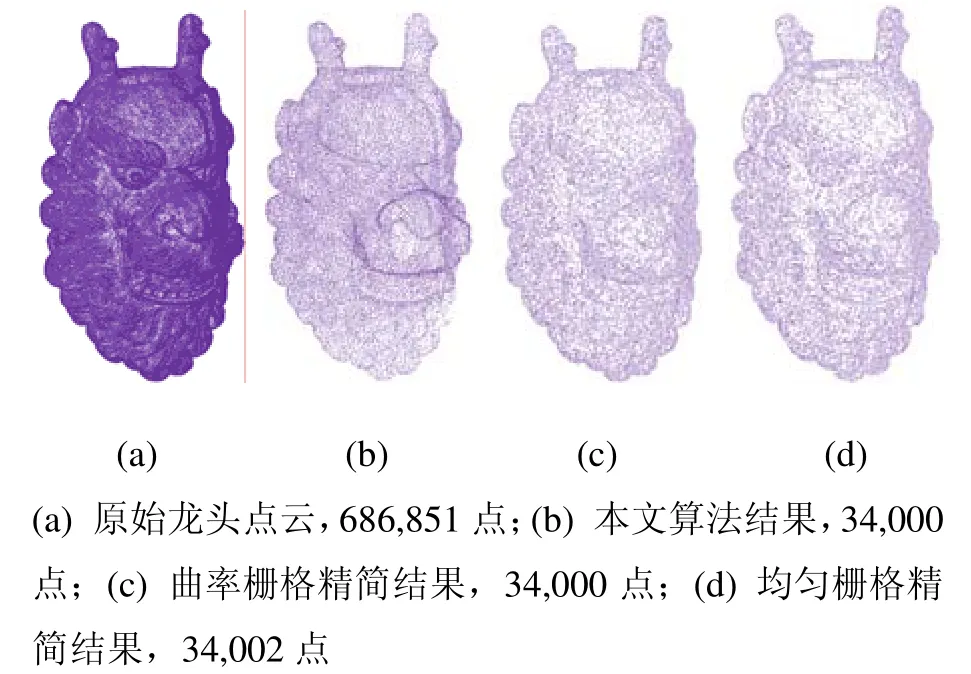
图11 龙头模型点云精简

本文采用Cignoni[27]等方法定量计算了精简点云重构曲面与原始点云之间的距离，本文算法与曲率栅格方法结果的平均距离误差分别为0.0329 与0.1556。这是由于该数据背面是光滑曲面，曲率栅格方法未能均衡曲率采样与均匀分布。如图12所示，本文算法在平坦区域形成了良好的分布因而误差比曲率栅格方法低，在曲率较大区域由于采样点数量相对稀疏因而误差比曲率栅格方法高。

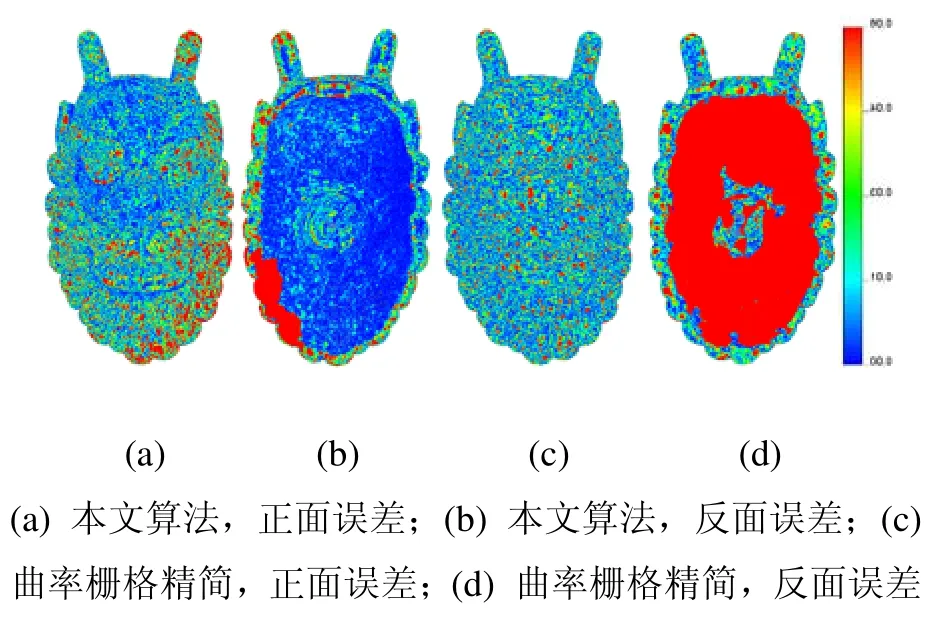
图13 龙头模型点云精简误差分析

5 结 论

本文提出了面向逆向工程、用于消除原始扫描点云中存在无效背景数据、冗余采样、分布不均匀等问题的点云选择与精简算法。点云选择算法支持套索UI接口，通过套索多边形的矩形覆盖与点云八叉树节点投影之间的包含关系剔除大部分点在多边形内测试，达到了商业软件的交互性能。点云精简算法利用Poisson-disk采样控制简化后点云的分布，与经典曲率栅格方法的比较结果表明本文算法具有保持尖锐边特征、保持边界、分布均衡的优势。

[1]Wang W. Reverse engineering technology of reinvention [M]. New York: CRC Press, 2011: 6-11.

[2]Weyrich T, Pauly M, Heinzle S, et al. Post-processing of scanned 3D surface data [C]//Proceedings of Eurographics Symposium on Point-Based Graphics.New York: ACM Press, 2004: 85-94.

[3]Geomagic studio. Geomagic studio user’s guide [M].Carolina: Geomagic Studio, 2008: 8-12.

[4]Inus Technology. RapidForm2004 user guide and tutorial [M]. Korea: Inus Technology Inc, 2004:59-62.

[5]张丽艳, 周儒容, 蔡炜斌, 等. 海量测量数据简化技术研究[J]. 计算机辅助设计与图形学学报, 2001,13(11): 1023-1119.

[6]Lee K H, Woo H, Suk T. Point data reduction using 3D grids [J]. The International Journal of Advanced Manufacturing Technology, 2001, 18(3): 201-210.

[7]Pauly M, Gross M, Kobbelt L P. Efficient simplification of point-sampled surfaces [C]//Proceedings of the Conference on Visualization,Washington D C: IEEE Press, 2002: 163-170.

[8]Haines Eric. Point in polygon strategies, graphics gems IV [M]. San Diego: Academic Press, 1994:24-26.

[9]Li Jing, Wang Wencheng, Wu Enhua. Point-in-polygon tests by convex decomposition [J]. Computers &Graphics, 2007, 31(4): 636-648.

[10]Zalik B, Kolingerova I. A cell-based point-in-polygon algorithm suitable for large sets of points [J].Computers & Geosciences, 2001, 27(10): 1135-1145.

[11]Yang S, Yong J H, Sun J, et al. A point-in-polygon method based on a quasi-closest point [J]. Computers& Geosciences, 2010, 36(2): 205-213.

[12]Linsen L. Point cloud representation. Universitat Karlsruhe [M]. CS technical report, 2001: 6-8.

[13]Song H, Feng H Y. A progressive point cloud simplification algorithm with preserved sharp edge data [J]. The International Journal of Advanced Manufacturing Technology, 2009, 45(5-6): 583-592.

[14]Yu Zhiwen, Wong Hansan, Peng Hong, et al. ASM:an adaptive simplification method for 3D point-based models [J]. Computer-Aided Design, 2010, 42(7):598-612.

[15]Shi Baoquan, Liang Jin, Liu Qing. Adaptive simplification of point cloud using k-means clustering [J].Computer-Aided Design, 2011, 43(8): 910-922.

[16]Song Hao, Feng Hsiyung. A global clustering approach to point cloud simplification with a specified data reduction ratio [J]. Computer-Aided Design, 2007,40(3): 281-292.

[17]Moenning C, Dodgson N A. Intrinsic point cloud simplification [C]//Proceedings of the 14th International Conference on Computer Graphics and Vision. Moscow, 2004: 1147-1154.

[18]Kang E C, Kim D B, Lee K H. Balanced feature-sensitive point sampling for 3D model generation [J]. The International Journal of Advanced Manufacturing Technology, 2007, 38(1-2): 130-142.

[19]Lastra M. An efficient parametric algorithm for octree traversal [J]. Journal of WSCG, 2000, 8(2): 212-219.

[20]Feito F R, Torres J C, Urena A. Orientation, simplicity,and inclusion test for planar polygons [J]. Computers& Graphics, 1995, 19(4): 595-600.

[21]Kobbelt L P, Botsch M, Schwanecke U, et al. Feature sensitive surface extraction from volume data [C]//Proceedings of the ACM SIGGRAPH. New York:ACM Press, 2001: 57-66.

[22]Zheng Y, Fu H, Au O K C, et al. Bilateral normal filtering for mesh denoising [J]. IEEE Transactions on Visualization and Computer Graphics, 2010, 17(10):1521-1530.

[23]Dunbar D, Humphreys G. A spatial data structure for fast poisson-disk sample generation [J]. ACM Transactions on Graphics, 2006, 25(3): 503-508.

[24]Fu Yan, Zhou Bingfeng. Direct sampling on surfaces for high quality remeshing [J]. Computer Aided Geometric Design, 2009, 26(6): 711-723.

[25]Klein J, Zachmann G. Point cloud surfaces using geometric proximity graphs [J]. Computers &Graphics, 2004, 28(6): 839-850.

[26]Zhao Hanli, Fan Ran, Wang Charlie C L, et al.Fireworks controller [J]. Journal of Visualization and Computer Animation, 2009, 20(2-3): 185-194.

[27]Cignoni P, Rocchini C, Scopigno R. Metro: measuring error on simplified surfaces [J]. Computer Graphics Forum, 1998, 17(2): 167-174.