激光多普勒冷却场中中性钠原子的耗散力特性

朱保华，黄 静，张宝武

(1．桂林电子科技大学，广西 桂林541004;2．贵州民族学院，贵州贵阳550000;3．中国计量学院，浙江 杭州310018)

1 引言

如果利用两束同频率、同强度、同偏振方向、沿相反方向传输的光束作用在原子上，当原子静止时，则原子所受到的合力为零，这是因为两束光的波矢方向相反。但是，当原子沿着光的传播方向具有某一运动速度时，该原子就会感受到一个力的作用，且该力的大小与原子运动速度成比例，而方向要依赖于激光的频率。若激光频率调谐至低于原子的共振频率，由于多普勒频移的存在，则与原子运动方向相反的那束激光的频率对于原子而言是处于蓝失谐状态，因此也就越接近于原子的共振。同样，与原子运动方向相同的那束激光的频率对于原子而言处于红失谐状态，故此也就进一步远离原子的共振。因此原子与其运动方向相反的激光束的相互作用会更强，由于耗散力的作用，这样也会进一步减小原子的运动速度，此即为激光多普勒冷却的基本机理［1－2］。

2 二能级钠原子光学布洛赫方程

原子与激光场相互作用的过程中，系统的密度算符ρ包含了二者相互作用的有效信息，故此可以通过求解激光场与原子系统的密度算符ρ来描述激光场中原子的运动问题。由于哈密顿量H与光学布洛赫方程的密度算符ρ之间的关系为［3］:

则对于二能级原子的四个密度矩阵算符 ρgg，ρeg，ρge及 ρee而言，有:

式中，下标“g”表示基态;“e”表示激发态。

考虑到原子与激光场的耦合，则当二者相互耦合时，上述的方程具有如下的特殊形式［3－4］:

其中，Γ－1为激发态的辐射寿命。在接下来的讨论中认为原子的密度算符可以直接通过把激光场的运动和自发辐射的贡献直接相加来得到，则总的密度算符为式(2)和式(3)之和，即:

上式即为具体的光学布洛赫方程。在稳态条件下，ρee和 ρgg均趋于一个常值，而 ρeg及 ρge则分别会按着 e－iωLt，eiωLt进行振荡。当作用时间达到特征时间Γ－1后，系统就达到了上述的稳态情况。结合式(4)和密度算符的迹守恒条件ρee+ρgg=1，厄米共轭特性条件 ρeg=ρge*则可以求解出稳态条件下ρeg的值，即为［5］:

将式(5)代入ρee的表达式，则可以得到:为饱和系数;Δ为反转粒子数密度;I为光强;Is为饱和光强。由式(6)可知，激发态的粒子数ρee在饱和参数S0较小的条件下，随该饱和参数S0的增加而线性增加。

则其余三个密度算符也可以求解出其具体形式，分别为:

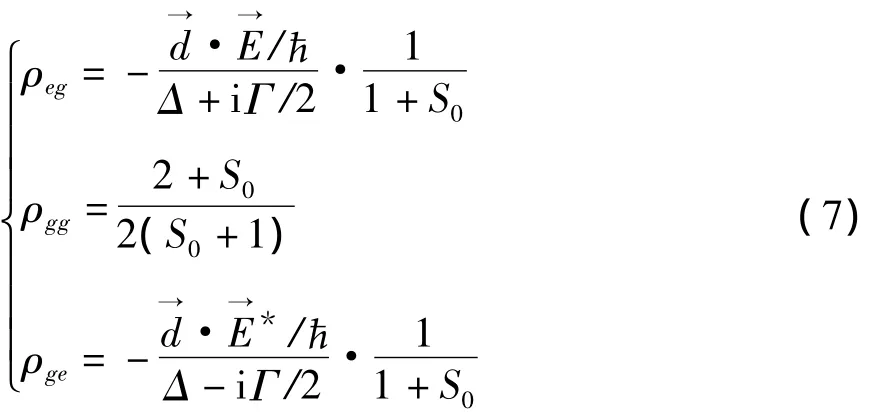
由式(7)可知当 S01时，ρee趋于。由于激发态的粒子以速率Γ进行衰减，且在稳态条件下激发速率和衰减速率相等，则激光场总的散射速率可以表示为［5］:

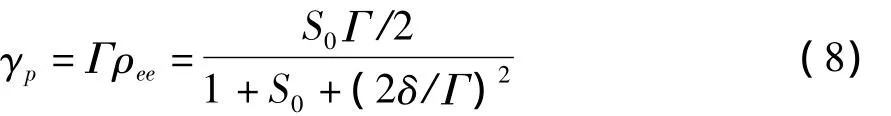
当激光场强度较大时，S01，则γp饱和于为跃迁过程的功率展宽线宽。

3 耗散力特性分析

图1给出了不同饱和参数S0条件下线宽的展宽和激光失谐量之间的关系。由图可以看出当饱和参数S0较大时(S0＞1)，功率展宽的轮廓具有较大的展宽程度，这是由于当饱和参数较大时，随着边沿区域激光强度的增加，其吸收过程也会随之加强，而中心区域的原子却早已处于激发态，故此，轮廓中心区域的吸收已经达到了饱和，而边沿区域的吸收却未达到饱和。

其中

则上式可以表示为:

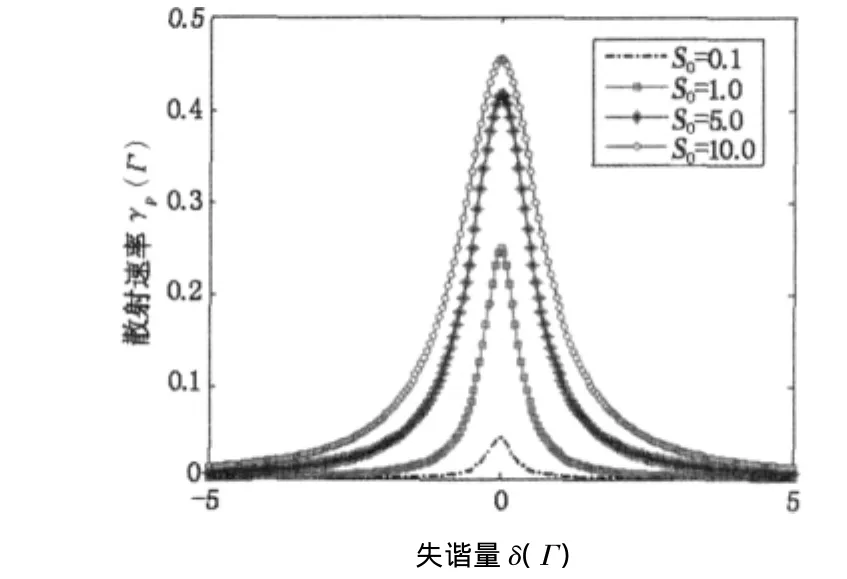
图1 激发散射速率与失谐量之间的关系

从上面的分析中可知，在稳态条件下Γ的数值即为激发态上所观察到原子的平均几率(即原子处于激发态上的平均几率)，该值来自于吸收过程之间的竞争。该吸收过程将会对激发态的粒子数有贡献，同时也会刺激自发辐射过程的进行，而该自发辐射过程会使激发态的粒子数减少，使基态上的粒子数增加。而Γρee的值表示稳态条件下，当激光照射原子时的自发辐射率。当饱和参数值S0较小时，该自发辐射率与激光强度成正比，当激光强度增大时，饱和参数S0变的远远大于1，则稳态值ρee趋于1/2，这就意味着原子将会有一半的时间处于激发态上，在这种情况下，自发辐射率趋于Γ/2。

对于激光行波场而言，可以表示为:

则密度矩阵方程［6］为:

将式(10)代入式(11)，在一级近似条件下进行积分，可得:

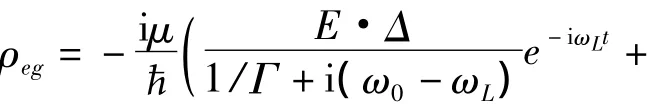
在旋波近似条件下，上式可以简化为:

考虑到多普勒频移，则有:

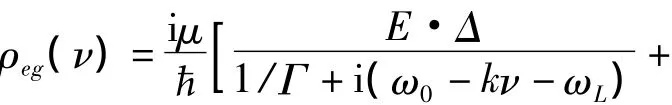
于是可以得到原子的极化为:

在电偶极近似条件下，根据量子力学可知，激光场中原子所受的力为激光场的梯度与原子极化的标积，即为:

将式(10)、式(15)代入式(16)可得:

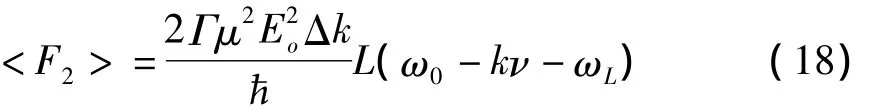
根据式(7)中引进的饱和参数，且令δ=ωL－ω0为激光失谐量，则行波场作用于原子的力最终可以表示为:

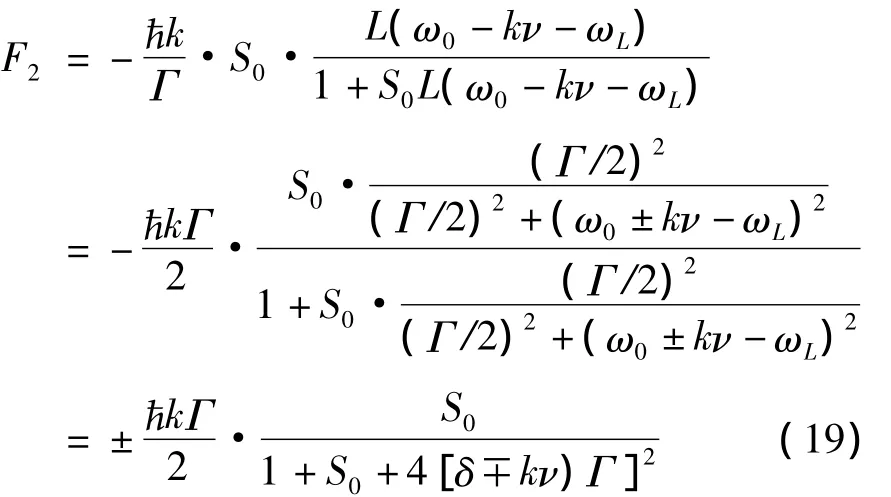
式(17)对时间求平均，可得:

对于由式(19)所给出的力F2而言，当处于激光场中的原子具有动量为m时，该原子吸收激光场动量为k的光子后，原子的动量将会发生变化，其相应的速度也会产生量值为Δν=k/m的变化。假若此时与同向，则原子将受到一种加速作用，反之当与反向，则原子将会受到一种减速的作用。原子吸收光子后将通过自发辐射重新回到基态，释放出的光子是各向同性的，多次自发辐射平均起来，则对于原子动量变化的贡献为零。这样，原子在每一光子吸收和再发射过程中平均得到Δν的净速度变化。对于钠原子而言，在389 nm的共振辐射激光场作用下，每个吸收－自发辐射过程所引起的速度变化为1．8 cm/s，由于此力与自发辐射有关，所以称该力为自发辐射力，也称为耗散力。

由式(19)可见，该耗散力具有共振的性质，当ωL=ω0，即当激光场的频率与钠原子的共振频率相同时此耗散力具有最大值。对于钠原子而言，在激光共振波长λ=389 nm的激光场作用下，钠原子所获得的加速度为2．8×105m/s2，该值为重力加速度的约105倍，可见在耗散力的作用下，钠原子的运动速度将会发生较大的改变。

图2给出了耗散力的共振特性，可见对于钠原子而言，当激光场的频率与钠原子的共振频率相同时，钠原子所受到的激光场耗散力最大，达到了2×10－20N。

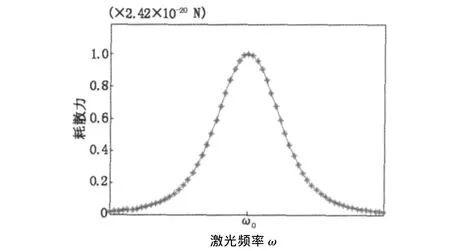
图2 耗散力与激光场频率间的关系

图3 给出了δ=－Γ条件下该行波场对原子所施加的力与饱和参数S0之间的关系，从中可以看出，随着S0的增加(激光场强度增加)，该力F也随之增加并趋于饱和，且其饱和值为 Fmax=kΓ/2。由于上述耗散力的作用，使得钠原子在激光场运动时将会获得一定的加速度。

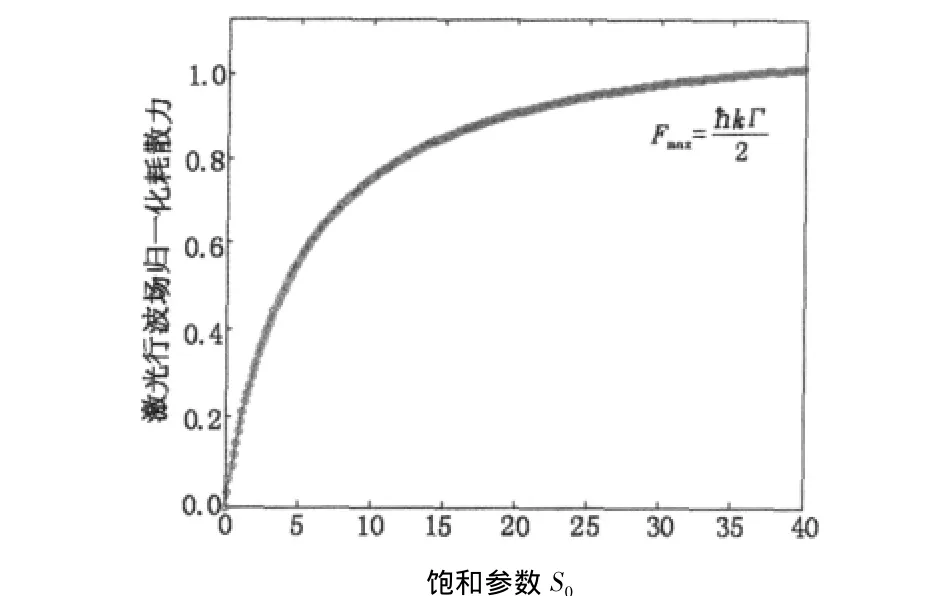
图3 激光行波场中钠原子所受力与饱和参数S0间的关系

图4 给出了激光场强度一定(S0=1)时，不同失谐量条件下原子速度与所受激光场耗散力之间的关系，从中可以看出当激光失谐量为线宽的一半，即δ/Γ=－0．5时，该激光场耗散力达到最大值。

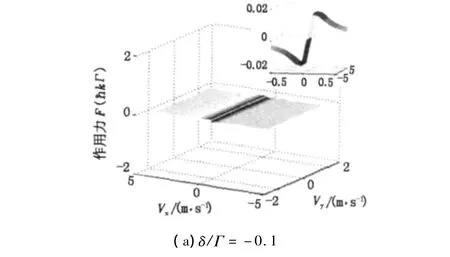
图5给出了不同饱和参数条件下激光失谐量与激光场对原子的阻尼系数之间的关系。从图中可以得知，当激光强度较小，失谐量较小时，原子所受到的阻尼系数β与激光功率及激光失谐量均成线性关系。当激光失谐量为原子线宽的一半，即 δ=－0．5Γ时，该阻尼系数达到最大值。这正好与图4的结果相吻合，但是当激光失谐量大于0．5Γ，光强大于饱和强度Is时，β达到饱和甚至开始降低。这是由于饱和跃迁所导致的，此时原子的吸收速率仅仅依赖其速度。以铬原子在激光场中受到的阻尼力为例，铬原子对应的跃迁能级为7P4→7S3，相应的跃迁波长为λ=425．55 nm，故每个光子所携带的动量为 k=15．6 ×10－28kg·m/s，该跃迁所对应的寿命为31．77 ns，假定有50%的粒子处于激发态，则激光场中铬原子所能获得的阻尼力高达2．46×10－20N，相应的加速度为2．8×105m/s2，这要远远大于电场或磁场所带来的效应。

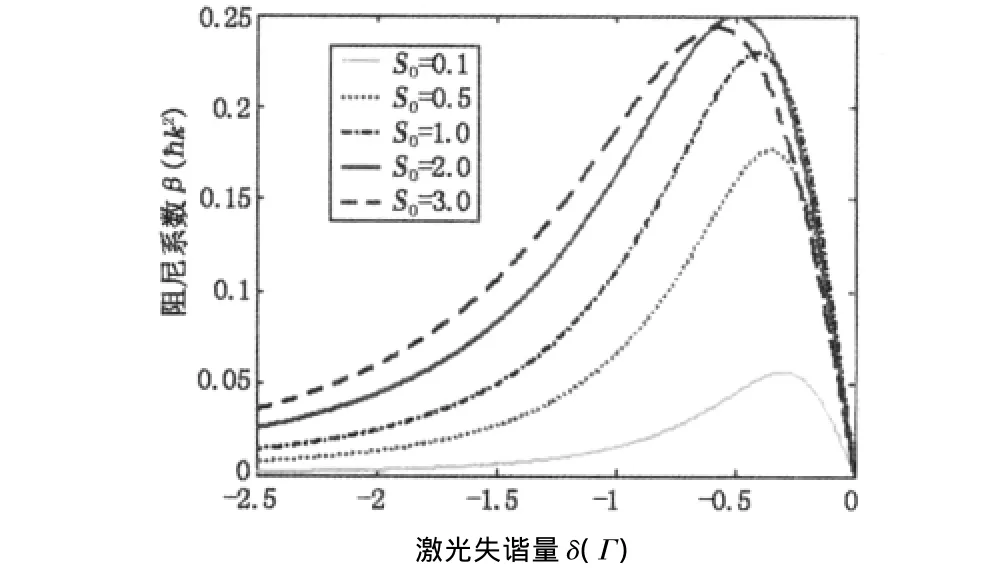
图5 不同饱和参数条件下激光失谐量与阻尼系数之间的关系

4 结束语

本文基于光学布洛赫方程和密度矩阵分析了多普勒激光冷却场作用下二能级中性钠原子的耗散力特性，并对不同激光场参数条件下的耗散力特性进行了仿真，仿真结果显示利用多普勒激光冷却场可实现中性钠原子的横向冷却，为沉积型原子光刻技术提供了重要的理论指导。

［1］ Wang Yuzhu，Xu Zhen．Laser cooling and its applications in science and technology［J］．Progress in Physics，2005，25(4):347 －352．(in Chinese)王育竹，徐震．激光冷却及其在科学技术中的应用［J］．物理学进展，2005，25(4):347 －352．

［2］ Zhang Wentao，Li Tongbao．Development of ultra-high vacuum chromium atomic sources in atom lithography［J］．Laser ＆ Infrared，2007，37(2):155 －157．(in Chinese)张文涛，李同保．用于铬原子光刻的超高真空原子源的研制［J］．激光与红外，2007，37(2):155 －157．

［3］ PD Lett，W D Phillips，SL Rolston，et al．Opticalmolasses［J］．J．Opt．Soc．Am．B，1989，6(11):2084 －2107．

［4］ Zhang Baowu，Zhang Wentao，Ma Yang，et al．Collimation of chromium beam by one-dimensional doppler laser with large collimating slit［J］．Acta Phys．Sin，2008，57:5485－5490．

［5］ Zhang Baowu，Li Tongbao，Ma Yan．One-dimensional doppler laser collimation of chromium beam with a novel pre-collimating scheme［J］．Chinese Optics Letters，2008，6:782－784．

［6］ M Mutzel，U Rasbach，D Meschede．Atomic nanofabrication with complex light fields［J］．Appl．Phys．B，2003，77:1－9．

［7］ Zhang Wentao，Zhu Baohua，Huang Jing，et al．Chromium atom deposition in elliptical standing wave filed［J］．Acta Phys．Sin，2011，60:103203 －1 －5．

［8］ Zhang Wentao，Zhu Baohua，Huang Jing，et al．Influence of divergence angle on deposition of neutral chromium atoms using laser standing wave［J］．Chinese Physics B，2012，32:033301 －1 －5．

［9］ Zhang Wentao，Zhu Baohua，Xiong Xianming．Analysis of nanometer structure for chromium atoms in gauss standing laser wave［J］．Chinese Physics Letters，2010，27:12302－1－4．