四阶混合边值问题的广义Jacobi-Petrov-Galerkin谱方法

2013-03-20孙涛，侯燕

郑州大学学报（理学版） 2013年4期

关键词：边值问题四阶广义

孙涛，侯燕

(1.上海金融学院应用数学系上海201209;2.周口师范学院计算机科学与技术学院河南周口466001)

0 引言

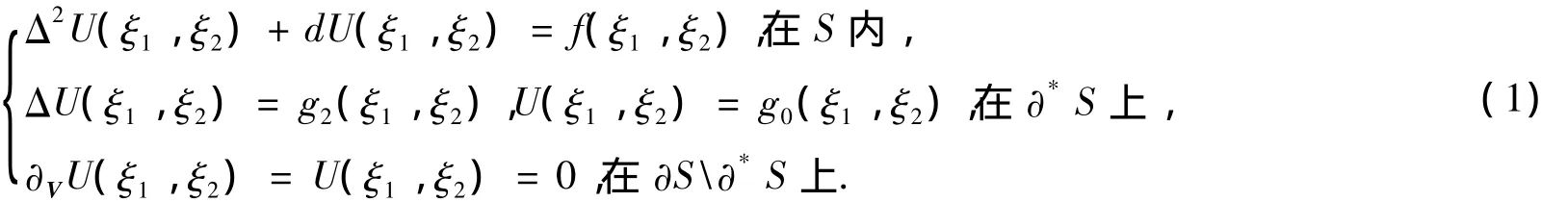
1 准备工作

对于任意的实数 α，β ＞－1，l次 Jacobi多项式 J(lα，β)(ξ)是如下 Sturm-Liouville问题的特征函数:

其对应的特征值为 λ(lα，β)=l(l+ α + β +1)，l=0，1，2，…．为了数值逼近，引入广义 Jacobi多项式［3］:

易知全体广义Jacobi多项式构成的系统{Y(lm，n)(ξ)}是区间Λ上以(1－ ξ)－m(1+ξ)－n为权函数的完备正交系．对于任意正整数N，记PN(Λ)为Λ上所有次数不超过N的代数多项式构成的集合．又定义多项式集合P0N，m，n(Λ)={φ ∈ PN(Λ)∂kξφ(－1)=0，当0≤k≤n －1时;∂kξφ(1)=0，当0≤ k≤ m －1时}．显然，

2 广义Jacobi-Gauss-Lobatto插值

用 ζ(Gα，N，β

，)j(0 ≤ j≤ N)表示 Jacobi多项式 J(Nα+，1β)(ξ)的 N+1 个按递减顺序排列的不同零点．由文献［4］可知，存在相应的 Christoffel系数 ω(Gα

，N，β，)j，

0 ≤ j≤ N，使得

当整数m，n≥1，0≤j≤N －m －n时，记

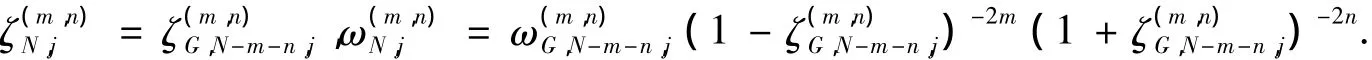
对任意整数r≥0，用Cr)表示上所有r次连续可微函数构成的空间．当r≥max(m－1，n－1)时，定义空间当时，可定义如下广义 Jacobi-Gauss-Lobatto 插值［3］:

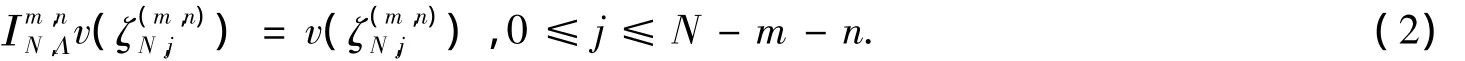
接着讨论另一个广义Jacobi-Gauss-Lobatto插值．为此，引入多项式qm，n，j(ξ)∈ Pm+n－1(Λ)［3］，

记δk，j为Kronecker符号，则多项式q－m，n，j(ξ)满足条件:

3 离散格式

由Lax-Milgram引理可知，当f∈L2(S)，g2∈H－1/2(∂*S)和g0∈H3/2(∂*S)时，问题(6)有唯一解．

为了数值求解问题(1)，须数值求解问题(6)．类似文献［5］中的思想，首先考虑问题(6)的边界广义Jacobi-Gauss-Lobatto插值逼近问题．为此，令Nb为非负整数，引入集合

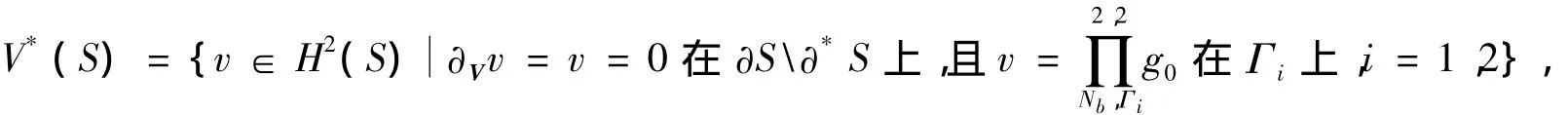
记数对N=(N，N)，ΡN(S)为区域S上所有次数不超过N的代数多项式构成的集合．则问题(7)的谱离散格式为:求 wN，Nb∈ VN，Nb(S)= ΡN(S)∩ V*(S)，使得

这样，利用广义Jacobi-Petrov-Galerkin谱格式(8)就可以求得问题(1)的数值解．

4 数值算法与结果

实际计算时，将数值解 wN，Nb(ξ1，ξ2)展开为

首先，在边界 Γi，i=1，2 上，根据插值条件(2)可以求得系数．然后，将(9)代入(8)，并取，即得到一个关于系数的线性系统．进一步令，则可将上述线性系统写成紧致矩阵形式．为此，

类似定义元素为 bl'1，l'2，l1，l2的矩阵 B．这样，即得(8)的紧致矩阵形式

从线性系统(10)中解出所有的系数w^(m，n)l1，l2，3≤l1，l2≤N，并将它们代入(9)即得问题(1)的数值解．

最后，用广义Jacobi-Petrov-Galerkin谱格式(8)对d=0，1时的问题(7)进行数值模拟．固定边界插值次数Nb=17，取实验函数为U(ξ1，ξ2)=(1 － ξ1)2(1 － ξ2)2sin(ξ1+ξ2)．为了度量数值误差，定义离散平均误差 EN，L2和离散最大模误差 EN，Max=

图1和图2分别描绘了log10(EN，L2)和log10(EN，Max)相对于自由度N的变化趋势．从图上可以看出，它们的值都随着自由度N的增大而迅速地减小，这说明作者提出的广义Jacobi-Petrov-Galerkin谱离散格式(8)是有效的，用该格式求出的数值解具有较高的逼近精度．