不确定混沌系统的无抖振滑模控制
2013-03-20吴艳敏
方 洁, 吴艳敏, 邓 玮
(郑州轻工业学院电气信息工程学院 河南郑州450002)
0 引言
混沌是自然界及人类社会中的一种普遍现象,自混沌概念被提出以来,已有许多中外学者对混沌系统展开研究,提出了各种混沌控制方法,并取得了一系列研究成果[1-2].滑模变结构控制作为非线性控制的重要方法,由于它对系统参数摄动、外界干扰、系统不确定性等具有完全鲁棒性,因此受到国内外学者的广泛重视.目前已有许多学者将其应用到具有不确定性混沌系统的控制与同步研究中[3-6].然而,实际系统由于切换装置不可避免地存在惯性,滑模变结构控制系统在不同的控制逻辑之间来回切换,因而导致实际滑动模不可能准确地发生在切换面上,容易引起系统的剧烈抖动.这一抖振现象已成为滑模变结构控制理论在实际应用中的主要障碍.如何消除抖振而又不失强鲁棒性,是滑模变结构控制实际应用时必须解决的首要问题.目前研究者已提出了许多消减抖振的方法,但大都以降低控制的准确性及增大闭环稳定到达时间为代价,且只能减小抖振,无法从根本上消除抖振[7-9].
基于以上讨论,作者针对一类具有模型不确定性和外界干扰的混沌系统,设计了动态滑模面和无抖振滑模控制器,实现了混沌系统的追踪控制.该方法不需要预先知道模型不确定性和外界扰动的上下界,通过设计包含积分项和微分项的动态滑模面,用控制输入的一阶导数处理符号函数,有效地避免了常规滑模变结构控制中符号函数引起的抖振问题.理论分析和仿真结果表明了该方法的有效性.
1 问题描述
考虑如下形式的混沌系统:

其中,x∈Rn为系统状态变量,f(x,t)∈R为连续光滑非线性函数,Δf(x,t)是系统模型不确定性和外界干扰,u(t)为待设计的控制输入.
设目标轨道为[x1d,x2d,…,xnd],其中,[x1d,x2d,…,xnd]=[xd,x·d,…,xd(n-1)],则可得误差系统为

作者的目标是设计合适的自适应滑模控制器,使得对于任意初始条件,误差系统满足

假设1 在一般情况下,混沌系统的状态轨迹都是有界的,因此假定模型不确定性和外界扰动Δf(x,t)是有界的,即存在正常数α,使得是未知界值.
假设2 模型不确定性和外界扰动Δf(x,t)的导数是有界的,即存在正常数β,使得是未知界值.
2 无抖振滑模控制器设计
2.1 设计滑模面
设计滑模面如下:

其中,滑模面参数 ci,i=1,2,…,n为合适的正常量.
传统滑模控制中的控制器包含符号函数,会引起抖振现象.为了获得光滑可微的控制输入,抑制抖振,可考虑设计合适的动态滑模面,进而用控制输入的一阶导数来处理符号函数,从而有效地抑制抖振.基于以上滑模面,可定义动态滑模面如下:
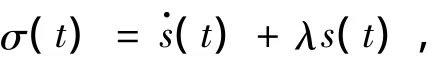
其中,λ >0,是一个常量.
注1 当误差系统到达滑模面上时,有

对s(t)求导可得
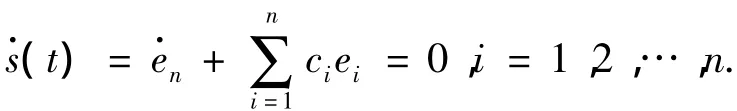
即

于是可得滑模面上的动态方程

可写为如下线性定常自治系统:

为了确保动态滑模面稳定,滑模面参数ci,i=1,2,…,n的选择需满足矩阵A的所有特征值均具有负实部.
2.2 设计滑模同步控制器
为了确保误差系统轨迹到达并保持在已设定的滑模面上,可设计滑模控制器为


相应的参数自适应律为

定理1 对于具有模型不确定性和外界干扰的混沌系统(1),在控制器(3)和自适应律(4)的作用下,误差系统(2)将渐近收敛到零.
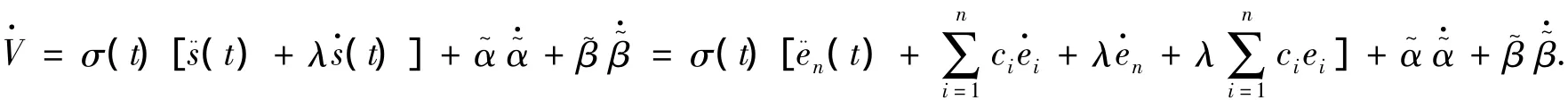
将误差表达式(2)代入可得

将控制器表达式(3)代入可得
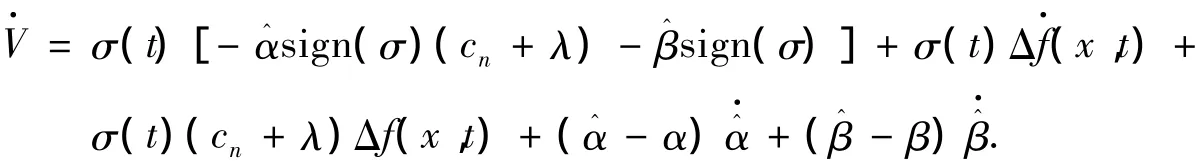

由假设1、假设2可得
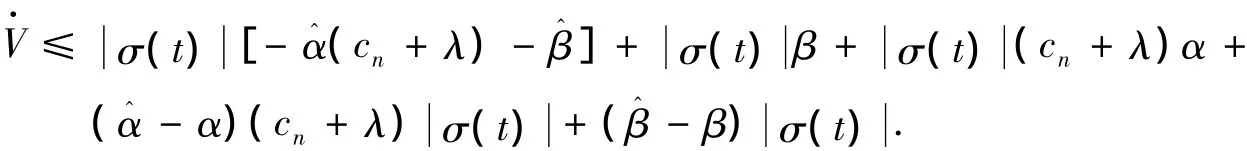
整理可得

由V·≤0可得,σ∈L2.由Barbalat稳定性定理可得,当t→∞时σ→0.由注1、注2可得,选择合适的滑模面参数ci,i=1,2,…,n,即可使误差系统渐近稳定.定理证毕.
3 仿真实验
以下列受控混沌系统为例进行仿真实验,其状态方程为

在仿真实验中,取 c1=c2=c3=5,λ =5.混沌系统的初始值为(0,0.2,0.2),自适应参数的初始值为(0)=0.5,0)=0.2.目标轨道为 xd=sin(πt/2),仿真结果如图1、图2 所示.对比图1(a)、(b)可知,在控制器的作用下,系统(5)由混沌态转变为周期态.由图2(a)、(b)、(c)可知,在施加控制后,系统的状态变量均能渐近追踪参考信号,实现追踪控制;由图2(d)、(e)可知闭环系统稳定后,滑模面函数趋于零值,控制输入无不期望的震荡;图2(f)为未知参数α,β的估计值变化曲线.
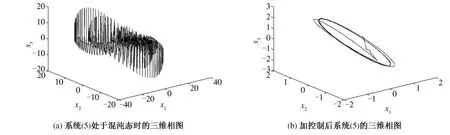
图1 系统(5)的三维相图Fig.1 Three dimensional phase diagram of equation(5)
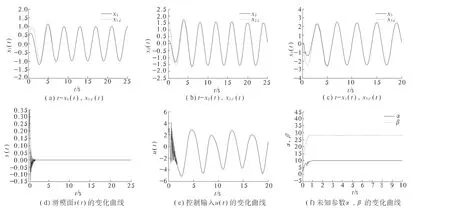
图2 无抖振滑模控制仿真图Fig.2 Simulation diagrams with chatter free sliding mode control
为了验证该方法的优越性,再以文献[10]中传统的滑模控制方法对系统(5)进行仿真实验,仿真结果如图3所示.对比可知,传统的滑模控制方法虽然也能实现追踪控制,但存在较大的抖振.

图3 用文献[10]方法时的控制仿真图Fig.3 Simulation diagrams with controller in reference[10]
4 结论
基于Lyapunov稳定性理论和滑模控制方法,实现了具有模型不确定性以及外界干扰的混沌系统的追踪控制.控制器设计中引入既包含积分项又包含微分项的动态滑模面,控制量u·(t)中包含符号函数,为不连续量,但u(t)为连续量,有效地避免了常规滑模控制中符号函数引起的抖振问题.数值仿真实验表明了该方法的鲁棒性和实用性.
[1] 付士慧,魏红军,刘洋.具有双向耦合的混沌系统的完全同步[J].郑州大学学报:理学版,2012,44(3):29-33.
[2] 方洁,邓玮,姜长生,等.具有扇区非线性输入的混沌系统函数投影同步[J].系统工程与电子技术,2012,34(9):1872-1877.
[3] Dadras S,Momeni H R.Adaptive sliding mode control of chaotic dynamical systems with application to synchronization[J].Mathematics and Computers in Simulation,2010,80(12):2245 -2257.
[4] Roopaei M,Sahraei B R,Lin T C.Adaptive sliding mode control in a novel class of chaotic systems[J].Communications in Nonlinear Science and Numerical Simulation,2010,15(12):4158 -4170.
[5] Zribi M,Smaoui N,Salim H.Synchronization of the unified chaotic systems using a sliding mode controller[J].Chaos,Solitons and Fractals,2009,42(5):3197 -3209.
[6] Pourmahmood M,Khanmohammadi S,Alizadeh G.Synchronization of two different uncertain chaotic systems with unknown parameters using a robust adaptive sliding mode controller[J].Communications in Nonlinear Science and Numerical Simulation,2011,16(7):2853 -2868.
[7] 刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005:4-8.
[8] 禹东川,孟庆浩.不确定时变混沌系统的一种自适应无抖振变结构控制[J].物理学报,2005,54(3):1092-1097.
[9] Li Huaqing,Liao Xiaofeng,Li Chuandong,et al.Chaos control and synchronization via a novel chatter free sliding mode control strategy[J].Neurocomputing,2011,74(17):3212 -3222.
[10] Dadras S,Momeni H R,Majd V J.Sliding mode control for uncertain new chaotic dynamical system[J].Chaos,Solitons and Fractals,2009,41(4):1857 -1862.
