MOTOMAN-UP6机器人运动学分析及仿真

徐呈艺，李业农，周小青，焦恩璋，刘英

(1.南通职业大学机械工程学院，江苏南通226007;2.南京林业大学机械电子工程学院，江苏南京210037)

工业机器人可以看作是由一系列用关节(运动副)联在一起的构件所组成的具有多个自由度的开链型空间连杆机构。它由若干个构件用转动关节或移动关节串接而成，MOTOMAN-UP6 机器人都是由转动关节串接而成，如图1所示。开链的一端固定在机座上，另一端则是末端执行器［1］。机器人运动学研究的是这些连杆运动的几何关系，具体来说是末端执行器的直角坐标空间与机器人关节空间坐标之间相互转换的关系。通过建立的几何模型的运动去实现正运动学数学模型与几何模型的相互验证的过程是机器人运动学仿真的重要意义之一［2］。

AutoCAD 是由美国Autodesk 公司设计和发表的强有力的绘图软件，目前在我国工业、企业界应用十分普遍。它具有完善的图形绘制功能、强大的图形编辑和几何测量功能，可以进行多种图形格式的转换。现以AutoCAD 为平台，进行UP6 机器人的建模、仿真和测量，正运动学数学模型和CAD 模型仿真得到相互验证。通过ADAMS 对虚拟样机进行运动学仿真，得到了位移、速度和加速度的运动曲线并进行分析。

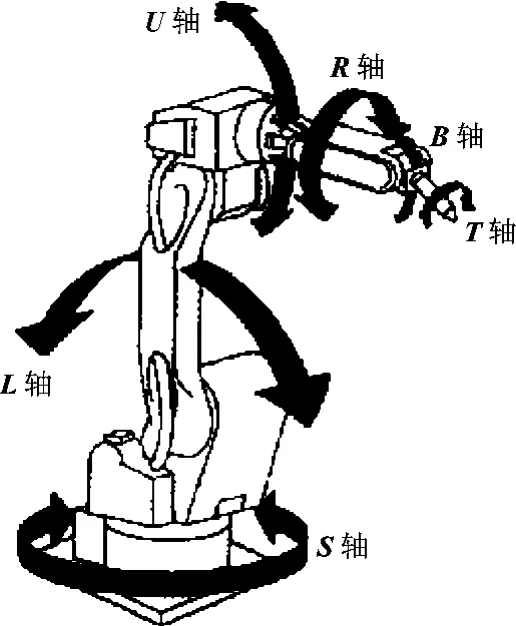
图1 UP6 机器人转动关节示意图

1 CAD 建模和构建D-H 坐标系

1.1 UP6 机器人的CAD 建模

MOTOMAN-UP6 机器人具有6 个自由度，6 个旋转轴分别为S、L、U、R、B 和T 轴。利用AutoCAD平台提供的实体建模、实体编辑和布尔运算等功能，可以很方便地建立各个构件的实体模块，如图2。根据各个构件的装配关系和位置尺寸利用AutoCAD 中剪切、复制、粘贴或移动等功能可以调整好机器人的初始状态的相对位姿关系［3－4］，如图3，x6、y6、z6为机械接口坐标系。

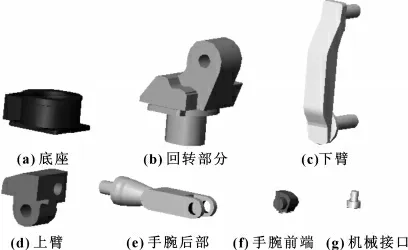
图2 机器人各构件模块

图3 UP6 机器人CAD 模型

1.2 D-H 坐标系的构建

UP6 机器人各构件的D-H 坐标系有多种方法，图4 是较简便的一种，为了计算方便，把机座坐标系建成图4 中x0－y0－z0位置，与UP6 机器人基坐标系一致，其中各关节运动量为0，z0，z1，…，z5为6 个旋转关节的轴线。坐标系建立遵循右手法则，所以在图4 中每个坐标系只标示出了两根轴。

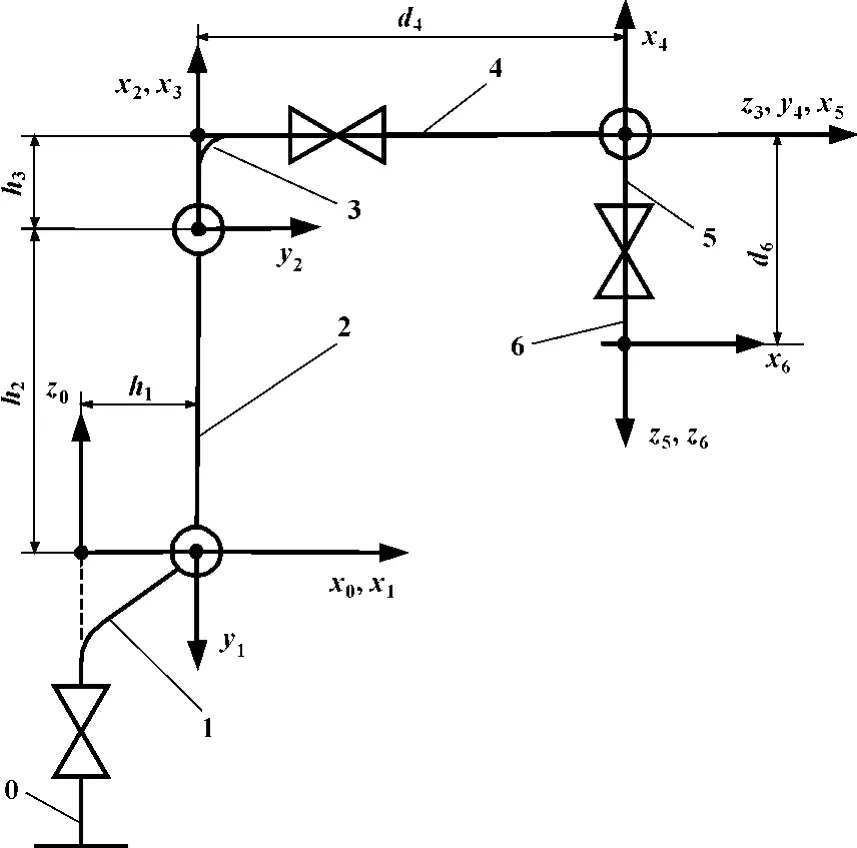
图4 UP6 机器人D-H 坐标系示意图

UP6 机器人构件坐标系的原则可以用转角θi、扭角αi、杆长hi和偏距di4 个构件参数来描述。zi轴取杆件i 与杆件i +1 副的轴线方向，而xi轴则取沿相邻两z 轴的公垂线方向。杆长hi是沿xi轴从zi－1轴量至zi轴的距离，规定与xi轴正向一致的距离为正。偏距di是沿zi－1轴从xi－1轴量至xi轴的距离，规定与zi－1轴正向一致的距离为正。扭角αi是绕xi轴从zi－1轴量至zi轴角位移，规定从xi轴方向观察逆时针方向的角位移为正。转角θi是绕zi－1轴从xi－1轴量至xi轴的角位移，规定从zi－1轴方向观察逆时针方向的角位移为正［1］。

2 UP6 机器人参数和运动学数学模型

2.1 UP6 机器人参数的确定

根据D-H 坐标系中参数的定义，扭角αi和杆长hi属于结构参数，偏距di和转角θi属于运动变量，而UP6 机器人关节没有移动副，所以偏距di是常量。可以将机构的结构参数和运动变量确定如表1所示。

表1 UP6 机器人的结构参数及运动变量

2.2 UP6 机器人正运动学数学方程

机器人任一连杆坐标系xi－yi－zi相对于机座坐标系的位姿可表示［5］

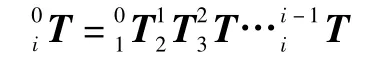
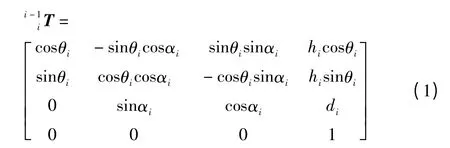
UP6 机器人从机座坐标系到工具坐标系的变换矩阵，即机器人运动学正解可表示为

将表1 中的结构参数分别代入式(1)，则有

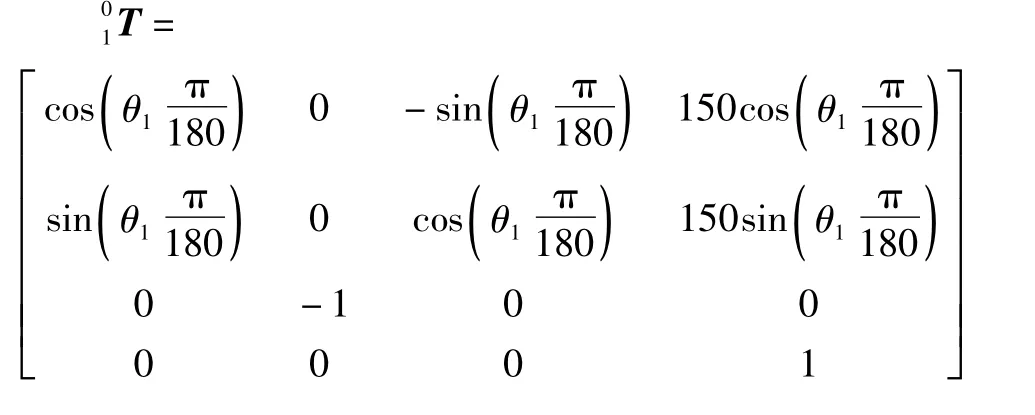
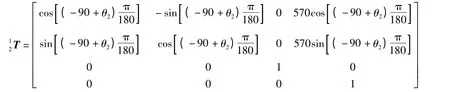
3 AutoCAD 模型仿真与数学模型的相互验证

3.1 起始位姿的验证

当UP6 机器人处于初始状态时，即6 个关节运动变量为0 时，将θ1= 0，θ2= 0，θ3= 0，θ4= 0，θ5=0，θ6=0 代入计算后则有

式(2)中的第4 列的前3 行元素代表机器人起始状态时机械接口坐标系原点相对于机器人基坐标系的位置参数，左上角3 ×3 旋转矩阵确定初始时机械接口坐标系相对于基坐标系的空间姿态。

通过AutoCAD 中“PROPERTIES”命令，可以得到机械接口坐标系原点的特性报告［2］，如图5，可知与式(2)计算的位置参数完全一致。再通过CAD 中“主视”、“左视”、 “俯视”等视图功能，很容易确定姿态也与式(2)的计算结果一致。

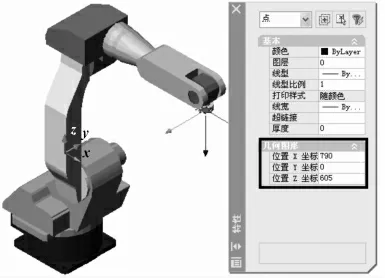
图5 从AutoCAD 中获取的机器人起始时机械接口坐标系位置

3.2 运动后位姿的验证

利用AutoCAD“三维旋转”功能分别驱动S，L，U，R，B 和T 轴6 个运动关节旋转，各关节对应运动角度分别为－10°，－20°，－30°，－40°，－50°和－60°。在驱动过程中，可以通过三维观察器、视图等方式检查构件是否存在干涉和碰撞问题，机器人前3 个关节的运动可以满足通常三自由度柱面坐标机器人的运动要求，即机械手可以实现回转部分、下臂和上臂的旋转，从而验证了连杆1，2，3参数设计的合理性。机器人后3 个关节的运动可以使机械接口坐标系具有不同的姿态，也说明了设计的参数是合理的。再使用“PROPERTIES”命令，得出运动后的机械接口坐标系原点的特性报告，如图6，得出(337.334 4，－99.338 4，1 135.135 3)一组参数。

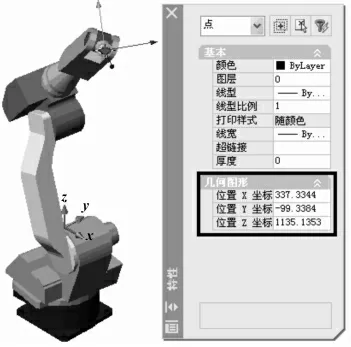
图6 从AutoCAD 中获取的机器人运动后机械接口坐标系位置

将各关节转角赋值θ1=－10°，θ2=－20°，θ3=－ 30°，θ4=－ 40°，θ5=－ 50°，θ6=－ 60°代入计算后则有

对比式(3)中的位置参数，其中运动后的x 和z 坐标值误差仅为0.000 1，符合要求。

确定空间姿态的3 ×3 方向旋转矩阵需要用到AutoCAD 中角度测量功能。为了方便并正确使用此功能，需把CAD 中的机器人基坐标系平移到机械接口坐标系的原点成为AutoCAD 中的世界坐标系x－y 平面需转换成与所测角度的对应两条直线所在平面一致或平行，这些可以通过CAD 中坐标系“三点方式”兼“旋转”等现有功能重新定义用户坐标系USC 实现。测量结果如图7—9所示。

图7 测量机械接口坐标系x6 轴分别与机座3 个坐标轴夹角

图8 测量机械接口坐标系y6 轴分别与机座3 个坐标轴夹角

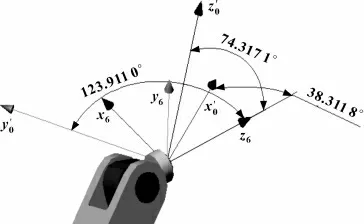
图9 测量机械接口坐标系z6 轴分别与机座3 个坐标轴夹角

根据图7 所测机械接口坐标系x6轴分别与机座3个坐标轴x0、y0、z0所夹角度，可得x6轴沿x0、y0、z0的分量

cos(x0，x6)=cos(55.943 8·π/180)=0.56

cos(y0，x6)=cos(34.421 2·π/180)=0.824 9

cos(z0，x6)=cos(85.584 8·π/180)=0.077

根据图8 所测机械接口坐标系y6轴分别与机座3个坐标轴x0、y0、z0所夹角度，可得y6轴沿x0、y0、z0的分量

cos(x0，y6)=cos(105.423 3·π/180)=－0.265 9

cos(y0，y6)=cos(87.780 4·π/180)=0.091

cos(z0，y6)=cos(16.323 6·π/180)=0.957 9

根据图9 所测机械接口坐标系z6轴分别与机座3个坐标轴x0、y0、z0所夹角度，可得z6轴沿x0、y0、z0的分量

cos(x0，z6)=cos(38.311 8·π/180)=0.784 6

cos(y0，z6)=cos(123.911 0·π/180)=－0.557 9

cos(z0，z6)=cos(74.317 1·π/180)=0.270 3

对比上述结果与式(3)中方向旋转矩阵，显然得到了验证。至此，针对机器人起始的位姿和运动后的位姿，运动仿真和数学模型都得到了较全面的相互验证，为UP6 机器人后续研究工作提供了重要的保障。

4 ADAMS 下的运动学仿真

ADAMS 软件是目前世界上最具权威性、使用范围最广的机械系统运动学和动力学分析软件，其仿真可用于预测机械系统的性能、运动范围、碰撞检测、峰值载荷以及计算有限元的输入载荷等［8］，但ADAMS 的建模功能较弱。这里，先把前面建立的AutoCAD 的各个构件的实体模块分别保存为* DWG格式文件，然后再逐个将这些图形转换成* IGES 格式，再导入ADAMS 平台，在机械接口添加夹持装置，夹持工件的中心在沿着机械接口坐标系z6正方向35 mm 位置，根据部件之间的连接方式添加相应的运动副和驱动约束，其中底座和大地之间要添加固定副。利用ADAMS 提供的传感器功能，可以限定机器人各关节的转角范围，当杆件之间有干涉时，仿真就会自动停止并报错［9－10］。

运动仿真时间设为定值2 s，再以两组不同的角速度进行运动仿真:

(1)UP6 机器人的S，L，U，R，B，T 各关节的角速度依次设置为10，－10，－10，－30，－30，－30 °/s，进行运动仿真后，得到工件中心轨迹曲线图，如图10，工件中心相对于机器人基坐标系随时间变化的位移、速度和加速度等运动曲线图，如图11—13所示。

图10 机器人夹持工件中心轨迹曲线

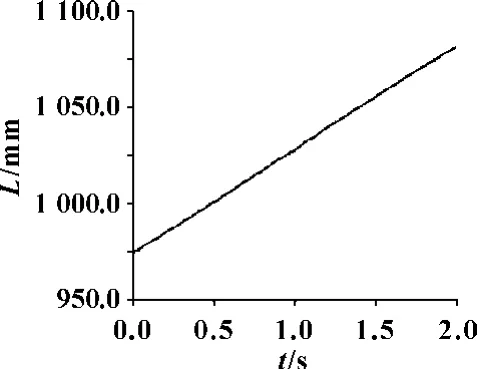
图11 机器人夹持工件中心合成位移曲线

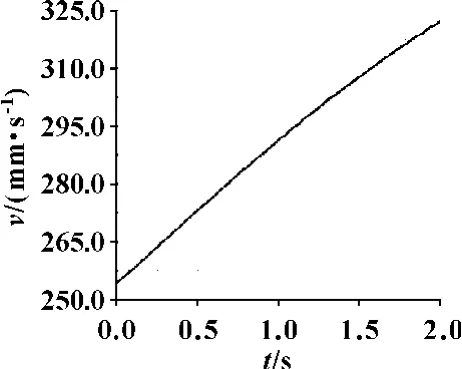
图12 机器人夹持工件中心合成速度曲线

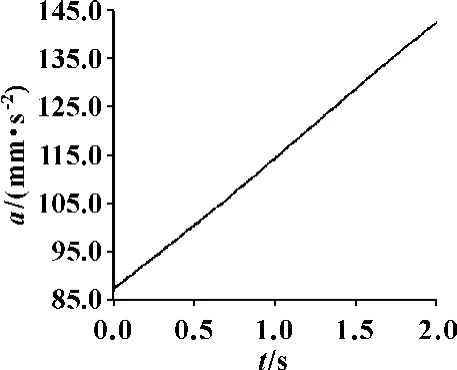
图13 机器人夹持工件中心合成加速度曲线

(2)UP6 机器人的S，L，U，R，B，T 各关节的角速度依次设置为 30，－ 30，－ 30，－10，－10，－10 °/s，进行运动仿真后，得到工件中心轨迹曲线图，如图14，工件中心相对于机器人基坐标系随时间变化的位移、速度和加速度等运动曲线图，如图15—17所示。

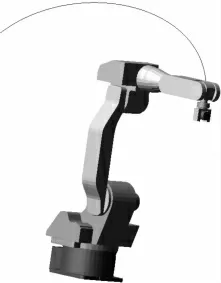
图14 机器人夹持工件中心轨迹曲线

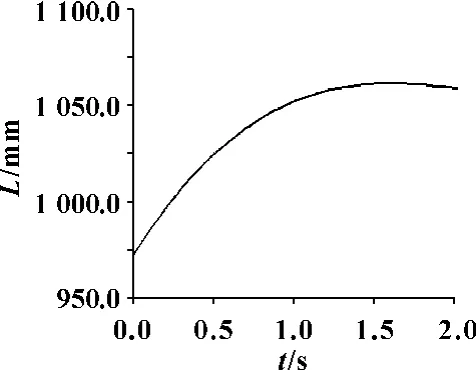
图15 机器人夹持工件中心合成位移曲线

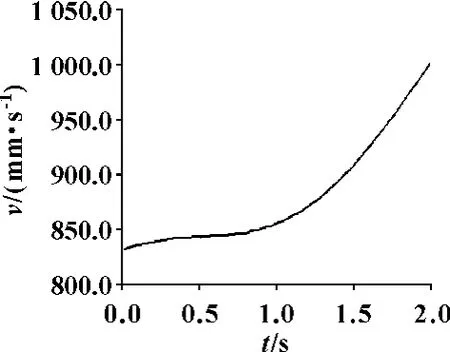
图16 机器人夹持工件中心合成速度曲线

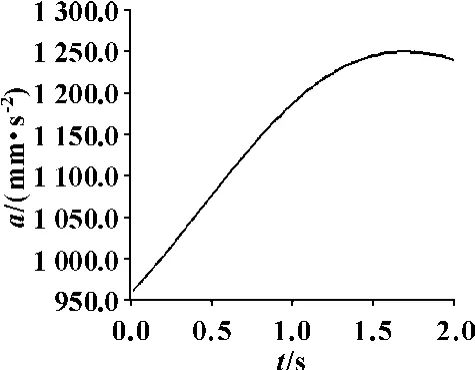
图17 机器人夹持工件中心合成加速度曲线

从以上两组位移、速度和加速度的运动曲线图可以看出:机器人末端运动轨迹和各运动曲线变化连续缓和，没有突变现象，说明机器人运动时，各关节运动灵活，各活动部件运动平稳，无冲击现象，并且杆件之间也没有出现干涉报警错误;当前3 个关节的角速度相对于后3 个关节角速度较小时，末端轨迹范围较小，各运动曲线变化相对平缓，位移、速度和加速度随时间增加而增大，接近线性变化;而当前3 个关节的角速度相对于后3 个关节角速度较大时，末端轨迹范围较大，位移、速度和加速度在前1 s 和后1 s 的变化趋势都有较大的不同。由此可以得出:机器人运动时间一定的情况下，各关节的角速度对末端运动性能影响不同，前3 个关节的角速度相对于后3 个关节的角速度对机器人末端运动性能影响更大。

5 结束语

建立了MOTOMAN－UP6 机器人的运动学正解数学模型和CAD 模型，通过AutoCAD 对起始和运动后的机器人进行仿真和测量，使得正解数学模型与CAD 模型仿真在位置和姿态方面得到了较全面的相互验证。

用ADAMS 完成了该机器人运动学的动态仿真，得出了末端执行器中心的位移、速度和加速度等运动性能曲线，分析了关节对末端运动性能的影响。从这些运动曲线图可以判定该机器人运动方案的合理性、轨迹规划的可行性，为轨迹控制和离线编程等研究和应用打下了基础。

借助于AutoCAD 的几何建模、测量和三维操作等现有功能，在探索机器人方面做了部分仿真和验证性的工作，具有简单、直观形象和效率高等优点，拓宽了AutoCAD 的应用领域。

【1】周伯英.工业机器人设计［M］.北京:机械工业出版社，1995.

【2】焦恩璋.以AutoCAD 为平台的机器人运动仿真研究［J］.计算机辅助设计与图形学学报，2001，13(10):932－936.

【3】焦恩璋，陈美宏.弧焊机器人与数控变位机协同作业规划［J］.电焊机，2009，39(12):78－80，84.

【4】焦恩璋，陈美宏.VS50 机器人运动学分析［J］.煤矿机械，2010，31(6):79－81.

【5】李振伟，张红兵.基于MOTOMAN-UP6 的自由曲面精整加工研究［J］.机床与液压，2010，38(9):18－20，48.

【6】JIA Songmin，HADA Y，YE Gang，et al.Distributed Telecare Robotic System Using CORBA as a Communication Architecture［C］//Robotics and Automation，ICRA'02.IEE International Conference，2002:2202－2207.

【7】朱世强，王宣银.机器人技术及应用［M］.杭州:浙江大学出版社，2001.

【8】芮执元，魏兴春，冯瑞成.基于ADAMS 的虚拟样机技术及其在机构设计中的应用［J］.科学技术与工程，2006，19(6):3111－3114.

【9】焦恩璋.用仿真规划机器人轨迹的研究［J］.煤矿机械，2009，30(8):52－54.

【10】杨成文，张铁.基于ADAMS 和SCARA 机器人运动学仿真研究［J］.机床与液压，2011，39(21):118－120，114.