基于感知器神经网络的金属磁记忆检测管道缺陷分析

龚利红，李著信，许红，刘书俊

(1.中国人民解放军后勤工程学院军事供油工程系，重庆401331;2.重庆通信学院军事电力工程系，重庆400035)

超过80%的现代工业设备的结构破坏都是由疲劳失效引起的［1］，在不伤及构件材料的前提下，有效判别在役设备构件的应力变形缺陷状况非常有现实意义。由俄罗斯科学家DOUBOV 教授提出的金属磁记忆(Metal Magnetic Memory)诊断技术能有效地对铁磁构件的早期应力集中进行无损检测［2］。一旦金属磁记忆检测出法向分量过零点，即可判定裂纹存在，但却不能通过单项指标有效区分是应力集中还是宏观裂纹［3－4］。因此，如何将多项指标综合在一起，通过有效的数学模型来识别就显得十分必要。

人工神经网络(Artificial Neural Network，ANN)由于其良好的预测功能而被应用于各领域，应用最广泛的是BP 神经网络和径向基神经网络，这两种预测模型针对连续结果的预测效果较好，对于定性结果往往采取选择阈值分类的方法，但阈值是未知的，主观选择阈值可能造成误差。感知器神经网络(Perceptron Neural Network，PNN)是人工神经网络中的一种分类效果较好的方法［5］，文中将该模型用于管道缺陷检测的识别分析。

1 感知器神经网络的原理与方法

1.1 感知器神经网络的基本原理

感知器是前向型单神经元的网络，其网络基本结构如图1。

其中:ωi表示第i 个神经元与感知器的连接权重;xi表示第i 个神经元的状态，i=1，2，…，n。

感知器的外部输入数据为研究对象的自变量指标值，输出为感知器的状态值，由输入神经元、权重和阈值决定，通过对外部神经元的“感知”与“识别”，由运算函数得到输出，输出状态一般为0 和1。运算函数往往选取:

图1 感知器网络基本结构图

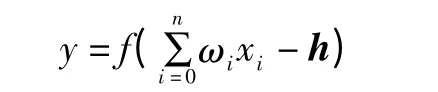
1.2 感知器的算法［6］

人工神经网络的训练是有监督的训练(training)，而感知器通过训练来调整权重以进行分类感知和识别。其算法如下:

(1)随机赋权重的初值，且ωi(0)≠0;

(3)求第k 次输出y(k)，并调整权重ωi(k+1);

(4)若y(t)=Ti，则训练结束，否则返回(3)。

2 管道缺陷的金属磁记忆分析的应用实例

2.1 数据集

数据来源于易方博士对X60 管线钢材质管道进行的缺陷识别实验［7］。在40 组实验数据中，应力集中21 例，宏观裂纹19 例，检测了每例的4 项指标，分别记为:小波包频带能量增量(%)X1、峰峰值(A/m)X2、切向梯度X3、法向梯度X4。实验样本的4 项指标数据见图2。

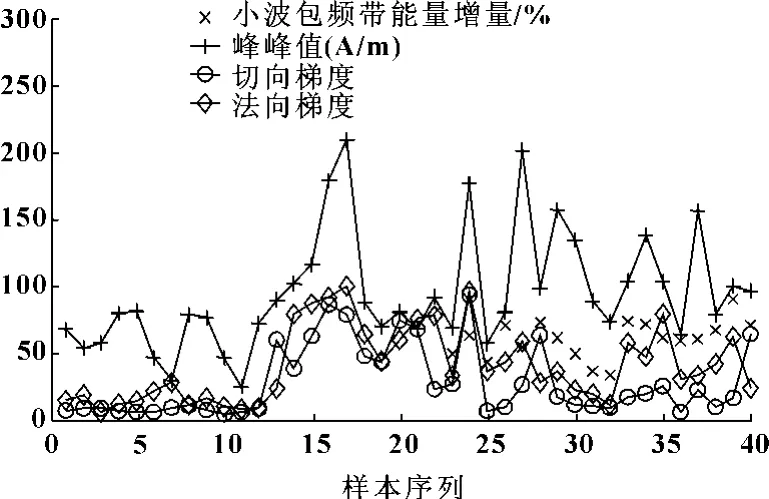
图2 实验样本的四项指标值

2.2 管道缺陷的线性感知器神经网络识别仿真

从应力集中类别和宏观裂纹类别中各随机抽取10 个样本组成训练样本集，其余20 个样本作为检测样本集，按照感知器神经网络的原理，作100 次计算机诊断模拟，迭代次数设置为200，最小误差设置为0。得到最高诊断正确率95%(有3 次)，最低诊断正确率35%，100 次模拟的平均正确率为71.2%，见图3。任意抽取最高诊断正确率的一次模拟，其训练误差见图4。

图3 线性判别正确率的计算机模拟

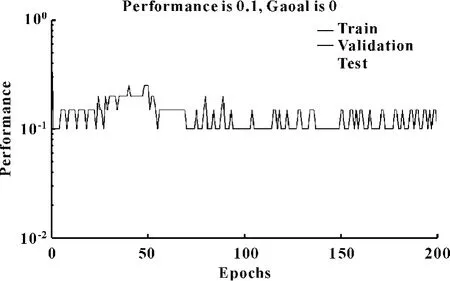
图4 一次最佳诊断效果的网络训练误差

2.3 管道缺陷的非线性感知器神经网络识别仿真

线性判别模型最高正确率能达到95%，但100次模拟的平均正确率较低，因此，考虑改进模型，并考虑增加非线性项来模拟效果。先考虑简单的完全二次项。

2.3.1 带完全二次项的非线性仿真

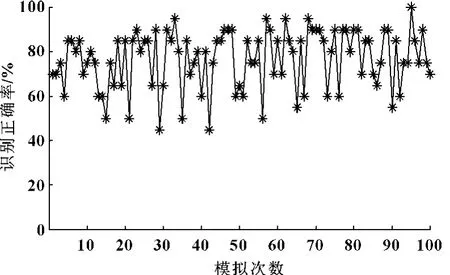
图5 完全二次项的识别正确率模拟结果

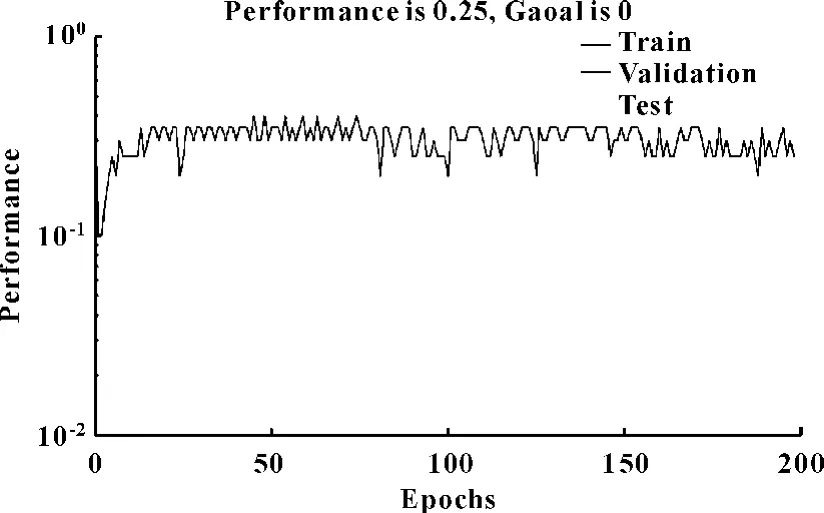
图6 完全二次项的一次最佳诊断效果的网络训练误差

2.3.2 非线性的进一步分析及仿真

由上述分析可知，增加非线性项有助于提高诊断正确率，而且指标的选择对正确诊断起着决定性的作用，由此，对上述的10 项指标作因子分析来筛选。由KMO 及Bartlett 检验可得，χ2=946.2，p=0，说明可以采用因子分析;KMO =0.762，说明因子分析的可信度高。因子分析的结果得到两个主成分，

从主成分结果可以看出，除x21 外，其余指标均归于第一主成分，但综合所有项时诊断效果不好，说明要继续剔除指标。x2x3、x2x4、x3x4的权重最大，均为0.932。另一方面，x2x3、x2x4、x3x4三者显著相关，相互均不独立，其中x3x4与x2x3、x2x4的相关系数最高，分别达到了0.973 和0.866，因此，最后仅选择x3x4，由它和x1、x2、x3、x4组成非线性的自变量向量来诊断。按照上述模拟方法，得到此时100 次模拟的平均正确率为90.7%，有大幅度的提高，有7次正确率达到了100%，最低正确率65%，如图7所示。任意选择一次正确率为100%的模拟，其训练误差如图8，网络训练误差和线性情形没有什么差别。

图7 带交叉二次项的识别正确率模拟结果

为了进一步分析非线性模型与线性模型的差异，将图2所示的线性情形的100 次模拟结果与图7所示的非线性情形100 次模拟结果作独立样本t 检验，检验结果为方差不齐性，t =－ 12.509，p = 7.727 ×10－27≤0.01，说明后者的平均正确率显著高于前者。

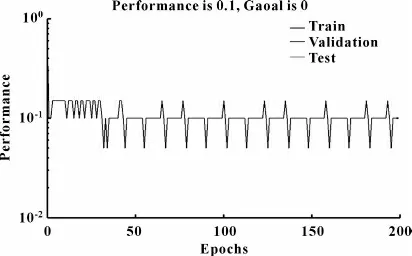
图8 一次非线性最佳诊断效果的网络训练误差

3 结论

(1)感知器神经网络模型对于管道磁记忆的缺陷线性识别效果不理想，通过模型的改进，提出了一种非线性指标的感知器模型。(2)感知器神经网络用于模式识别已经比较成熟，但用于管道磁记忆的缺陷识别分析尚未查到相关文献。文中从指标分析入手，构建综合切向梯度和法向梯度乘积项及4 项线性指标来识别管道缺陷，通过计算机模拟发现，其识别正确率相比线性情形有显著的提高，达到了较高的识别水准，有一定的创新性。(3)只有当训练样本线性可分时，感知器神经网络的训练误差才能到零，由于计算机模拟的随机性，样本没有经过筛选，故3 种情形的最优效果的训练误差均未达到0。上述的3 种情形中，前两种趋于稳定的迭代次数要比第三种情形要长。(4)感知器神经网络有时训练时间长，在实际应用中可以进行改进。在收集足够多的实验数据后，可以通过数据筛选的方法，选择最优的训练数据集，使得训练样本线性可分，从而减少训练时间，建立管道磁记忆检测缺陷的感知器神经网络识别模型，并构建自动识别系统应用于实际的管道检测工作。

【1】张立东，边境，刘贵民.漏磁的磁记忆检测技术［J］.检测技术，2005，24(1):79－80.

【2】DOUBOV A A.Screening of Weld Quality Using the Metal Magnetic Memory ［J］.Welding in the World，1998，41(3):196－199.

【3】周克印，张静，姚恩涛，等.构件隐性损伤的磁记忆检测方法研究［J］.南京航空航天大学学报，2004，36(6):715－717.

【4】任吉林，王东升，宋凯，等.应力状态对磁记忆信号的影响［J］.航空学报，2007，28(3):724－728.

【5】李坤，周晓兰，唐希雯，等.感知器算法在运动想象脑电模式识别中的应用［J］.计算机工程与应用，2006(25):230－232.

【6】飞思科技产品研发中心.神经网络理论与Matlab7 实现［M］.北京:电子工业出版社，2005.

【7】易方.油气管道金属磁记忆检测信号处理与缺陷识别技术研究［D］.重庆:后勤工程学院，2010.