基于Recurdyn的蛇形机器人的蜿蜒运动仿真

庞博，邓宏彬

(1.河北工程大学机电工程学院，河北邯郸056038;2.北京理工大学机电学院，北京100081)

蛇形机器人的冗余度极高，具有多自由度的运动能力，使其可以模仿出生物蛇的多种运动模式，在运动行进过程中蛇形机器人与地面多点甚至线或面接触，运动稳定性好，对地形的适应能力强，在很多领域具有十分广泛的应用前景。

目前研制出的蛇形机器人具有多种结构形式［1-3］，可实现多种运动模式［4-8］，蜿蜒运动作为生物蛇最典型的一种运动，是蛇形机器人运动模式研究的核心问题。本文以研制出的九关节蛇形机器人为研究对象，对蛇形机器人的蜿蜒运动机理进行了深入研究，在多体系统动力学仿真软件Recurdyn中建立蛇形机器人的运动模型进行仿真，最后对仿真结果进行了分析和说明。

1 蛇形机器人蜿蜒运动机理

1.1 简化的蜿蜒运动曲线

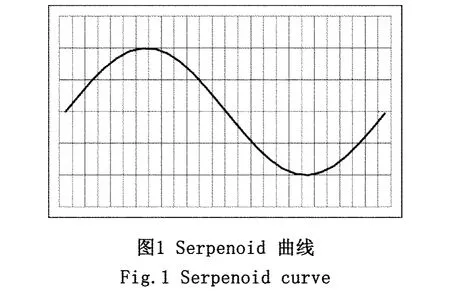
蛇进行蜿蜒运动时，通常采用 Serpenoid曲线［1］进行分析，如图1所示。

一个周期内，Serpenoid曲线的曲率方程为

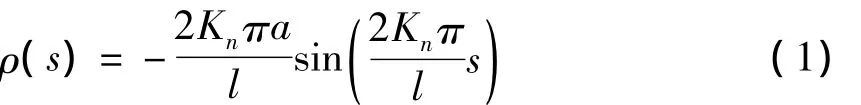
式中:l-蛇形机器人的总长;Kn-蛇形机器人体内传递波的个数;a-Serpenoid曲线的初始弯角; s-蛇形机器人沿Serpenoid曲线轴线方向的位移。

本文采用简化的Serpenoid曲线［2］作为蛇形机器人步态的产生方式，弧长为s处的曲率定义为

式中:a-Serpenoid曲线的初始弯角;b-常数。

将式(2)对s积分，可以得到Serpenoid曲线上弧长为s处切线方向与水平方向的夹角。将Serpenoid曲线近似为长度为l的线段的集合，l趋近于无穷时，两个相邻长度为l的线段在弧长为s处的夹角为

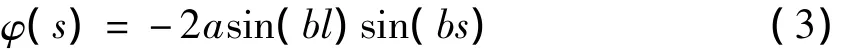
实际中蛇形机器人模块长度不可能无穷小，即l不可能趋近于无穷，以模块实际长度来拟合Serpenoid曲线，仍可以近似模拟的蜿蜒运动。

1.2 蜿蜒运动步态的产生

蛇形机器人的模块化关节长度为2l，当s=0，2l，4l，…时，蛇形机器人在各模块化关节处的转角为

式中:i-各关节的序号。

各关节的相对转角确定后，可使蛇形机器人确立静态的蜿蜒构型。蜿蜒运动中，蛇形机器人各个关节应沿Serpenoid曲线动态运动，s的取值应为随时间变化的序列，设s=ct，ct+2bl，ct+ 4bl，…，其中c为常数。令A=-2asin(bl)，ω= bc，β=2bl，动态情况下蛇形机器人在各模块化关节处的转角为

2 蛇形机器人的模型建立与仿真

2.1 蛇形机器人的模型结构

蛇形机器人模型如图2所示，结构上采用模块化关节设计，其整体机械结构由九个相同模块串联而成，各模块的尺寸为:直径65 mm，长238.5 mm。蛇形机器人的模块化关节类似于一个万向节机构，具有横纵两个方向的自由度，每个自由度由各自的电机和控制系统进行驱动与控制。通过模块化关节连接而成的蛇体具有高冗余度，可以使蛇形机器人实现多种姿态与运动模式。

2.2 仿真环境设置

蛇形机器人的初始姿态利用三维设计软件调整各段关节与万向节的角度来实现，然后导入RecurDyn中设定参数后进行虚拟仿真，导入后模型如图3(a)所示。RecurDyn的仿真环境设置如下:机器人各关节与地面使用实体接触(Solid Contact)，各参数设置如图3(b)所示。

各关节与万向节的约束采用转动副(Joint)，蛇形仿生机器人通过设定各转动副(Joint)的运动(motion)来模拟电机驱动情况下各关节运动。运动(motion)选用位移模式，即设置各转动副的位移时间函数。与地面水平的转动副位移时间函数均设置为0，即蜿蜒运动情况下水平方向的转动副不参与运动。与地面垂直的各转动副位移时间函数设置为

式(6)中，n根据各转动副位置依次取0～8，使参与运动的各关节转动副相位依次滞后从而产生蜿蜒运动。Recurdyn中step函数为3次多项式逼近阶跃函数，可用于定义一个光滑的阶跃函数。

2.3 仿真

式(6)中，参数A的大小决定了蛇形机器人蜿蜒曲线摆动的幅度;β的大小决定了蛇形机器人体内形成波的个数。设置仿真时间为30 s，步数为1 000，使模型的运动达到稳定。仿真包含以下情况:

情况1:保持ω和β不变，改变A的值。设置式(6)中ω=1，为了使蛇形机器人体内形成一个波，取β=0.7。每次仿真改变一次A值。蛇形机器人在不同幅值下的运动情况如图4所示。不同幅值下蛇形机器人的前进速度如表1所示。

情况2:保持A和β不变，改变ω的值。设置式(6)中A=0.7，为了使蛇形机器人体内形成一个波，取。每次仿真改变一次值。蛇形机器人在不同频率下的运动情况如图5所示。

不同频率下蛇形机器人的前进速度如表2所示。

情况3:保持A和ω不变，改变β的值。设置式(6)中A=0.7，ω=1。每次仿真改变一次β值。蛇形机器人在不同形成波个数下的运动情况如图6所示，不同频率下蛇形机器人的前进速度如表3所示。

表1 不同幅值下蛇形机器人的前进速度Tab.1 The forward speed of the snake-like robot in different amplitudes

表2 不同频率下蛇形机器人的前进速度Tab.2 The forward speed of the snake-like robot in different frequency

表3 不同形成波个数下蛇形机器人的前进速度Tab.2 The forward speed of the snake-like robot in different frequency

3 仿真分析

根据仿真数据绘制关系曲线如图7所示。

1)前进速度与幅值关系曲线图如图7(a)所示，图中可以看出，随着幅值的增加，蛇形机器人的前进速度有着明显的增加，实际中，蛇形机器人模块化关节角函数的幅值由关节设计的最大转角限制，设计的蛇形机器人前进速度最大的最优幅值为0.7rad。

2)前进速度与频率关系曲线图如图7(b)所示，图中可以看出，随着关节角函数频率的增加，蛇形机器人的前进的速度一直增加，实际中，蛇形机器人模块化关节角函数的频率受所选用电机的限制。

3)前进速度与频率关系曲线图如图7(c)所示，图中可以看出，随着蛇形机器人体内形成波个数的增加，蛇形机器人的前进速度越来越小，但波的个数太少的话会影响蛇形机器人的前进方向，无法形成完整的蜿蜒曲线。

4 结论

1)随着关节角函数幅值、频率的增加，蛇形机器人蜿蜒运动前进的速度随着增加。但是在实际中，关节角函数的幅值由关节设计的最大转角限制，关节角函数的频率受选用电机限制，因此通过合理地设计模块化关节、选择关节电机，可以增强蛇形机器人的蜿蜒运动性能。

2)当蛇形机器人模块化关节数目与蜿蜒曲线长度一定时，在形成波个数满足形成蜿蜒曲线的情况下，减少蛇形机器人蜿蜒曲线的形成波个数，有利于提高蛇形机器人前进速度。

3)提出的蛇形机器人能够在仿真环境下完成预定的蜿蜒运动，对进一步的样机实验具有重要指导意义。下一步需要对蛇形机器人的运动步态规划做进一步的完善，使其运动轨迹更加平滑，适合更多复杂的自然环境。

［1］HIROSE S.Biologically inspired robots-snake-like locomotors and manipulators［M］.Oxford:Oxford University Press，1993.

［2］MA S G，TADOKORO N.Analysis of creeping locomotion of a snake-like robot［J］.Autonomous Robots，2006，20:15-23.

［3］李斌，马书根，王越超，等.一种具有三维运动能力的蛇形机器人的研究［J］.机器人，2004，26(6):506 -509.

［4］孙红，马光荣.蛇形机器人一种基于Serpenoid曲线的蠕动步态机械设计与研究［J］.机械设计与研究，2008，24(1):40-44.

［5］王光荣.蛇形机器人蠕动、蜿蜒运动运动特性的研究［D］.上海:上海交通大学，2004.

［6］YAN CL，MA SG，LI B，et al.Modular universal unit for a snake-like robot and reconfigurable robots［J］. Journal of Advanced Robotics，2009，23(7-8):865 -887.

［7］WU XD，MA SG.Adaptive Creeping locomotion of a CPG-controlled snake-like robot to environment change［J］.Journal of Autonomous Robots，2010，28 (3):283-294.

［8］王南，王晶，平恩顺.基于ADAMS/Car的双横臂悬架的运动学建模与仿真［J］.河北工程大学学报:自然科学版，2010，27(4):55-58.