两种并联机构的静刚度及有限元分析

王南，高鹏，崔国华，郝丽红

(1.河北工程大学机电学院，河北邯郸056038;2.中国科学院深圳先进技术研究院，广东深圳518055)

并联机构的刚度是并联机构性能的重要指标，并且为并联机构的设计提供重要理论依据。对并联机构的建立精确的刚度模型，成为近年来研究学者的研究重点。陈吉清等［1］利用螺旋矢量法建立了并联机床刚度的数学模型，并对并联机床动态性能进行了分析。吕亚楠等［2］利用有限元法研究了一种冗余并联机床的静刚度。李育文等［3］用有限元法分析了一种6-UPS并联机床静刚度，并且考虑了并联机床的支链和机架的变形。王友渔等［4］借助子结构综合思想和Ansys参数化设计语言，构造了Trivariant和Tricept两种机械手的有限元模型，充分考虑了机构中各种铰链对并联机构处于不同位形时的整机静、动态特性的有限元快速重构技术。胡波等［5］提出了一种将3-RPS机构的变形和刚度转化为一个等效无约束反力的6自由度并联机构3-RPPS的变形和刚度进行分析。

在少自由度并联机构中，由于机构结构自身的原因，使得机构内部存在约束力/约束力矩，从而对整机的刚度精度产生重要影响，因此在分析中应予以考虑［6］。本文就3-RPS并联机构及其变种3-SPR并联机构建立含约束力/力矩的刚度模型，并利用商用有限元软件Ansys Workbench验证两种并联机构刚度模型的正确性。

1 系统简介

3-RPS并联机构是三自由度并联机构。由上下2个平台以及3个支链组成。其中3条支链由R、P、S3个运动副组成，支链通过R副与定平台相连，另一端通过S副与动平台相连，其中驱动力由P副提供。三条支链平均分布将动、定平台连接起来(图1-a)。3-SPR并联机构是3-RPS并联机构的变异模型，上、下两个平台通过3个SPR支链连接。一端由S副连接定平台，另一端由R副连接动平台。其中P副提供动力输出(图1-b)。

1.1 位置逆解

图2为两种并联机构的机构简图。建立笛卡尔直角坐标系B-XYZ，以定平台的中心点为坐标系原点B，X轴平行BB1且方向向右，Y轴沿BB2方向，Z轴垂直于面B1B2B3且向上。以动平台的中心点A建立动坐标系A-uvw，u轴方向AA1且方向向右，v轴沿AA2方向，w轴垂直于面A1A2A3且向上。

设定A点的初始坐标为(0，0，H)，动平台的任一位形可描述为动平台绕u轴旋转α，绕v轴旋转β，w方向的位移ZA。

封闭向量Li为

式中:qi-杆长;li-沿杆方向的矢量;Ai-点Ai在B-XYZ坐标系中的位矢;-动平台上Ai的坐标变化齐次矩阵。

由于机构本身的约束关系，可以得到

联立式(1)、式(2)、式(3)得杆长qi为

1.2 雅可比矩阵的求解［7］

设动平台的速度为V，则

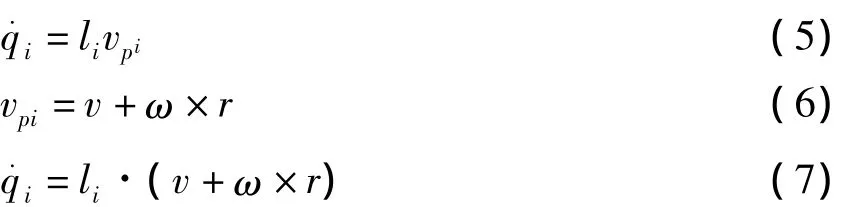
则微动平台的驱动映射雅可比矩阵JA为

ri球铰各点相对于动平台中心点的矢径

球铰点S的速度矢量AVi可表示为

AVi在R的投影Vui=0，可得

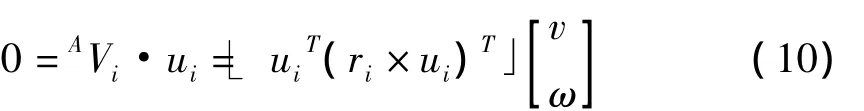
则可得到约束映射矩阵JC

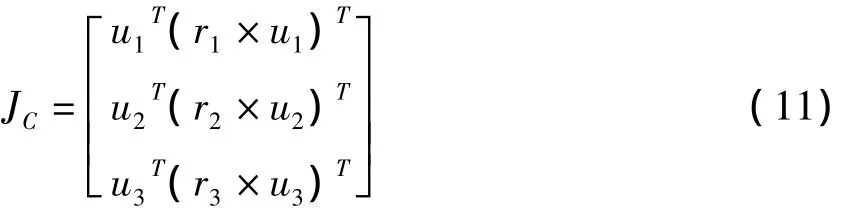
并可得到完整的映射矩阵

1.3 刚度矩阵的求解

各分支在驱动力Fai和约束反力Fpi的作用下产生变形，设约束反力Fpi产生的变形δri沿ri方向，可以得到

式中:A-杆的横截面积;Ee-弹性模量;ki-各分支的刚度系数。

由于δri很小，其方向可以看作是沿Fpi方向，也就是R副的方向，可知

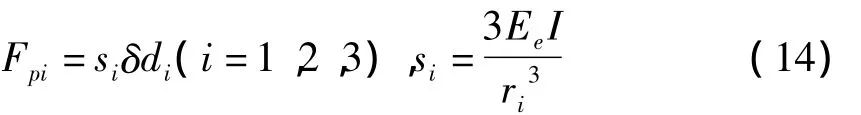
式中:EeI-分支的弯曲刚度;I-分支的惯性矩。

得到机构的刚度矩阵K为

由于3-SPR并联机构与3-RPS的结构类似，推导雅可比矩阵的过程同上。在刚度模型中，由于S副位于其支链的下面，其变形情况也与3-RPS类似，推导过程略。

2 数值算例

给定参数RB=100 mm，RA=80 mm，初始高度H=75 mm，

由两种并联机构的静刚度可以发现(表1)，Z方向的刚度值总比其它两个方向大，并且3-SPR并联机构的刚度比3-RPS的刚度要大。

3 有限元分析

并联机构的刚度模型是位形的函数，因此在应用有限元软件对并联机构分析时，定会针对不同位形对并联机构进行有限元分析［8］。利用Solidworks三维实体建模软件建立两种并联机构的实体模型，利用软件自身的装配将并联机构按照实际情况装配到一起。根据杆长，将并联机构调整到需要的位姿，然后导入到Ansys Workbench中，按照并联机构的运动副设置其连接条件。两种并联机构的材料按照弹性模量E=2.11e11 Pa，泊松比γ=0.3，屈服极限δ=350 MPa。整机模型采用四面体和六面体单元划分网格，单元数目为14 368，节点数为51 153。外载荷F=［10 -15 20］N，M=［-20 10 15］N/m。

表2中列出了两种并联机构在不同位形时的变形情况。结合表1可以看到理论分析值与有限元分析的结果的极为相近，说明刚度模型的准确性。纵向对比表2中位置Ⅰ位置Ⅱ位置Ⅲ的变形云图，Z方向的刚度总比其余两个方向大，即两种并联机构承受Z方向载荷能力强于其余两个方向。从两种并联机构的X方向变形云图中可以看出，两种并联机构在不同位形时，3-SPR并联机构在X方向的刚度均略大于3-PRS，跟理论分析的结果一致。

表1 两种并联机构静刚度Tab.1 Static stiffness of the two parallel mechanism N/m2

表2 两种并联机构各向变形云图Tab.2 Each direction deformation of the two parallel mechanism

4 结论

有限元软件验证结果表明，3-SPR并联机构的刚度性能优于3-RPS并联机构的刚度性能，两种并联机构的Z方向刚度均比X、Y两个方向的刚度大。

［1］陈吉清，兰凤崇.Stewart并联机床瞬时刚度分析与应用［J］.南京理工大学学报，2007，31(4):482-486.

［2］吕亚楠，王立平，关立文，等.一种冗余并联机床静刚度有限元分析与优化设计［J］.机械设计与制造，2008，2(2):1-3.

［3］李育文，张华，杨建新，等.6-UPS并联机床静刚度的有限元分析和实验研究［J］.中国机械工程，2004，15(2):112-115

［4］王友渔，赵兴玉，黄田，等.可重构混联机械手Trivariant和Tricept的静动态特性预估与比较［J］.天津大学学报，2007，40(1):41-45.

［5］胡 波，路懿.求解3-RPS并联机构刚度的新方法［J］.机械工程学报，2010，46(1):24-29.

［6］刘树青，吴洪涛.一种新型起重机器人的运动学分析与应用［J］.河北科技大学学报，2004，25(2):58-61.

［7］王南，张莉婷，郝莉红.空间3-UPU/UPU机构的刚度分析［J］.河北工程大学学报:自然科学版，2012，29 (3):85-87.

［8］LU Y，HU B.Analyzing kinematics and solving active/ constrained forces of a 3SPU+UPR parallel manipulator［J］.Machine and Mechanism Theory，2007，42 (10):1298-1313.