资源受限项目调度问题的探讨

刘 振

（中铁第四勘察设计院集团有限公司，430063，武汉∥高级工程师 ）

PERT（计划评审技术）和CPM（关键路线法）作为项目管理非常有效的工具，被广泛应用于项目计划和控制过程中。然而这两种方法都是假设项目使用的资源是无限供给的。但在城市轨道交通项目的实际执行过程中，可以使用的资源往往是受到一定限制的。如设备的订货、设备基础和预埋件的施工等，本来是平行任务，但由于受供货时间滞后、同型号不同厂家设备尺寸差异等影响，有些工序的开始时间只能向后推迟，待安排在前面的工序完成并且释放资源后才能开始执行。所以，根据PERT／CPM这两种方法编制的计划在资源受限的情况下一般不能够得到保证。由此产生了资源受限项目调度问题（Resource－Constrained Project Scheduling Problem，简为RCPSP）。该问题在理论上属于NP－hard问题［1］，即：项目中具有一系列相互关联的任务，其中，每一个任务可以采用几种模式完成，每一种模式以已知的工期和资源需求量为特征，在满足紧前关系和资源约束条件下产生一种使其管理目标为最优的调度方案。

1 资源受限项目进度问题的描述

典型的资源受限项目进度问题可描述如下［2］：

在一个项目中，包括J项活动，Pj为活动j的紧前活动集，j∈（1，2，…，J）；活动j＝1与活动j＝J为虚工作，即活动1是唯一最早开始的活动，活动J是唯一最晚完成的活动，均为不消耗资源且执行时间为0的活动。T为项目的合同工期。设活动j的完成需要的第r种资源量为kjr，执行时间为dj，第r种资源总量为常量Kr（r＝1，2，…，R），活动j的完成时间为TFj，At为在t时间段内正在进行的活动集合。典型的资源受限项目进度问题可建立如下数学模型：

式（1）是目标函数，表示项目总工期最短；式（2）代表项目活动间的紧前关系约束；式（3）代表每一阶段的资源使用量不能超过其最大量。

2 资源受限项目调度问题的分类

资源、任务和目标函数三要素组成了资源受限项目调度问题。资源的不同数量和类型，任务错综复杂的约束条件，再加上度量不同指标的目标函数，形成了种类繁多的RCPSP问题。通常采用文献［3］三段式分类方法对资源受限的项目调度问题进行分类。该方法采用机器排序的分类形式，用三个参数α，β，γ来描述RCPSP的类型，得到了多数学者的认同。以下简要介绍各段的含义。

1）段α描述问题的资源属性，包含3个参数：αl，α2，α3。

参数αl∈｛0，m｝描述了资源的种类，它可能是空，标记为0，也可能是一种资源或者是m种资源，αl＝0或m；参数α2描述了资源种类的特性。

按照文献［4］和文献［5］提出的资源分类法，可分为可更新资源（Renewable Resources）、不可更新资源（Nonrenewable Resources）和双重资源（Doubly Constrained Resources）三种。可更新资源是指在每个时段获得一定量的资源，这种资源的获得和消耗是以每一阶段为基础的（如运碴汽车和施工人员等）；不可更新资源是指在整个工期内只能获得一定量的资源（如原材料、能源等）；双重资源是指资源的获得和消耗既在工期的每一阶段受限，又在整个工期的总量上受到限制（如掘进盾构机等）。双重约束的资源分配问题可以被转化为相应的可更新资源和不可更新资源来处理。

α2∈｛0，1，T，1T，v｝，分别表示：资源类型（缺省），可更新资源，不可更新资源，双重资源，部分可更新资源。

参数α3∈｛0，vα｝描述了资源的使用量，通常用来表达可更新资源。α3＝0，时，表示可更新资源使用量为常数；α3＝vα，表示可更新资源使用量为变量。

2）段β描述问题的任务属性，包含8个参数。

参数β1∈｛0，pmtn，pmtn－rep｝描述了任务在执行时中断的可能性。当任务是不允许中断时，β1＝0。β1＝pmtn，表示任务可以在执行的过程中被中断，然后在中断点处继续加工，任务中断前后执行的时间的总和与不中断的执行的时间是一样的。此中断称为可续性中断。β1＝pmtn－rep，表示任务在执行过程中可被中断，但不允许在中断点处继续执行，必须从头开始。此中断被称为重复性中断。

参数β2∈｛0，cpm，min，gpr，prob｝描述了任务时序关系的约束特征，时序约束可以用一个网络图表示。

β2＝0时，表示任务相互独立，即任务之间没有时序约束。β2＝cpm，表示各任务之间是无延误的完成－开始时序关系。β2＝min，表示各任务具有最小延误时间的开始－开始，完成－开始，开始－完成，以及完成—完成的时序约束关系。β2＝gpr，表示任务间具有最小和最大延误时间的广义的时序约束关系。这里的最小延误时间是指：只有在其紧前任务开始（完成）一段时间后该任务才能开始（完成）；最大延误时间是指：任务应该在另一任务开始（完成）后的某一时间内开始（完成）。β2＝prob，表示任务的网络图具有一定的概率。

参数β3∈｛0，rj｝描述任务的准备时间，分别表示：准备时间为0，各任务需要不同的准备时间。

参数β4∈｛0，cont，d｝描述任务的工期，分别表示：任务的工期为离散的整数，任务的工期为任意实数，所有的任务具有相同的工期。

参数β5∈｛0，δj，δn｝描述交货期，分别表示：项目没有底线约束，任务的交货期，项目的交货期。

参数β6∈｛0，vr，disc，cont｝描述资源需求的特性，Β6＝0时，表示任务在同一执行模式下所需资源为常量。β6＝vr，表示任务在同一执行模式下所需的资源是变量，β6＝disc，表示任务的资源需求量是任务工期的离散函数。β6＝cont，表示任务的资源需求量是任务工期的连续函数。

参数β7∈｛0，mu，id｝描述任务的执行模式，分别表示：单执行模式，多执行模式，模式约束任务（此时任务集合被划分为不相交的子集，每个子集中的所有任务必须以相同的模式来执行）。

参数β7∈｛0，cj，per，sched｝描述数据流的性质。β7＝0，表示空。β7＝cj，表示任务之间的资金流动。，表示为静态的资金流。，表示任务之间为正的资金流。β7＝per，表示特定的资金流。β7＝sched，表示既包含资金流又包含时间流。

3）段γ描述项目调度问题的优化目标。优化的目标函数可分为两类。一类为正则目标函数，满足以下两个条件：①目标函数是求最小值；②目标函数是完工时间的单调非降函数，例如项目总工期最小、项目总成本最低或项目延误最小等。另一类为非正则目标函数，例如最大净现值、提前完工费用和误工费用最小等。下面介绍几种目标函数：γ＝Cmax，表示项目总工期最小。γ＝Tmax，表示项目误工最小。γ＝nT，表示加权误工任务数最小。γ＝npv，表示项目净现值最大。由上述分类中可以看出，该问题模型丰富，且多属于NP－hard问题，但求解困难。从20世纪60年代初至今，资源受限项目调度问题已吸引了大量学者的注意，有大量的研究成果从不同的角度研究了该问题。总的来说，求解该问题的算法可分为精确算法与启发式算法。智能算法为启发式算法的一类分支。对于城市轨道交通动辄上百亿元的大项目，应用此方法解决其调度问题，具有明显的优势。

3 资源受限项目调度问题的求解方法

一般来讲，RCPSP的求解关键要解决算法的表达形式，除了由算法本身所决定的进化机制外，主要由调度生产方案、编码方式和解码规则、相邻解的定义以及初始解的产生这几个部分组成。而相邻解的定义往往由编码方式和解码规则确定［6］；初始解一般是随机生成或者根据特定的编码方式结合一些优先规则生成。

3.1 调度生产方案

调度产生方案可分为串行调度方案（SSS）和并行调度方案（PSS）。两种方法都是对一个不完全计划进行扩展，直至生成一个完全计划。在工期的每个阶段，调度生产方案都会形成一个可行工作集（满足约束条件），然后根据某个优先权规则从该集合中选取一个或多个活动安排其进度，并将其转移到一个不完全计划集合，直到所有活动都安排完成为止。

3.1.1 串行调度方案

串行调度方案最早由文献［7］提出。串行调度方案包括n（n＝1，…，J）个阶段，每个阶段都存在一个不完全计划集合Sn和一个满足紧前关系约束的可行工作集Dn。在每个阶段，根据某个优先规则在集合Dn中选择一项工作，并指定该工作的开始时间为满足紧前关系约束和资源约束的最早可行时间（如果有多个工作具有相同的优先权，优先安排编号小的工作），然后将该工作从集合Dn移动到集合Sn中。当当前阶段为n＝J时，所有的工作都从集合Dn移动到集合Sn，Dn为空集。

3.1.2 并行调度方案

并行调度生成方案当前有两种算法：Kelley［7］和Brooks（Bedworth and Bailey）［8］。两种算法有所区别。当前沿用的主要是Brooks（Bedworth and Bailey）的方法。并行调度方案最多包括J个阶段，每个阶段对应调度时间tn；在tn时间已完成的工作集合为Cn，在tn时间正在进行的工作集合为An。同时，此时存在一个满足紧前关系约束与资源约束并可以在tn时间开始的可行工作集Dn。与串行方案不同的是，并行调度方案的不完全计划工作集由Cn与An两个集合构成。该方案从阶段n到阶段n＋1需要两步：第一步，将tn＋1阶段的时间设置为An集合中最早完工的工作的完成时间，然后将An集合内完工时间等于tn＋1时间的工作，从An集合转移到Cn集合，形成新的集合An＋1与Cn＋1，并计算剩余资源量，形成可行工作集Dn＋1。第二步，从Dn＋1集合中，按特定优先规则，选择一项工作（如果有多个工作具有相同的优先权，优先安排编号小的工作），将该工作开始时间安排在tn＋1时刻，并将其从Dn＋1集合中转移到An＋1集合；然后不断重复步骤二，直到Dn＋1集合为空。

3.1.3 两种方案的比较

文献［9］对这两种调度生成方案进行了比较和评价：当无资源约束时，两种调度方法都能生成最优调度；串行调度方法生成的调度通常是积极的，而并行调度方法生成的是非延迟调度。对于两种调度生成方案，并行调度生成方案搜索的解空间要比串行调度生成方案搜索的解空间小（并行方案的tn时刻总是等于上一阶段正在工作集合中最早的完工时间），因此在某些情况下，可能搜索不到全局最优解。Kolisch通过利用PSPLIB进行研究发现；当不考虑资源约束时，两种方案都能够产生最优解；当处理规模较大且有适当资源限制的问题时，串行方案比并行方案有较好的性能。

3.2 编码与解码

编码方式和解码规则，归纳起来可分为如下几类［6］。

3.2.1 任务列表

此类方法通过串行调度方案生成一个工作链表，各工作在链表中的顺序显然是满足紧前关系约束的。反之，如果给定一个满足紧前关系的工作链表，那么应用串行调度方案解码可以生成一个可行调度计划。但值得注意是，并行调度方案也适合这种方法的解码［10］。文献［11－18］采用了此类编码与解码方式。

3.2.2 优先权系数向量

此类方法给定一个J维向量，向量中的第j个元素代表工作j的优先权系数，那么针对该向量应用串行（并行）调度方案解码便可生成一个可行调度计划。文献［19－25］采用了此类编码方式。

3.2.3 优先规则链表

此类方法事先选定若干条优先规则构成优先规则集，再从中依次随机选择J条规则构成优先规则链表（一条编码）。解码规则既可以采用串行调度方案也可以采用并行调度方案。解码过程如下：在调度第j项工作时，采用编码中的第j条优先规则计算当前可调度工作集中各工作的优先权，并选择优先权最高的工作按照串行（并行）调度方案原则安排其开始时间，直至J项工作全部调度完毕。文献［13］采用了此种编码方式。

3.3 资源受限项目的求解步骤

基于智能算法的资源受限项目调度问题一般求解步骤：

第一步，确定编码方式与解码规则。这一步包括了两个方面：一是确定RCPSP与算法的映射，即编码方式，主要有上述介绍的三种；二是确定解码规则，包括进度生成计划。

第二步，确定初始化方法。一般是随机生成或者根据特定的编码方式结合一些优先规则生成。

第三步，确定算法的进化机制。主要与算法本身特性相关，即迭代寻优。

第四步，确定适应度值的计算方式。第五步，确定算法终止规则。算法结构流程一般见图1。

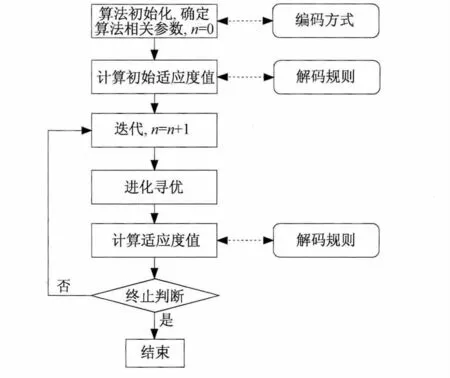
图1 RCPSP智能算法一般结构流程

4 结语

资源受限项目调度问题广泛存在于城市轨道交通工程领域以及其他重点、大规模建设项目。本文主要回顾了该问题在其项目管理环节中的呈现方式和基本分类，并对建模、调度生产方案、编码方式和解码规则加以详细阐述；重点介绍应用智能算法求解资源受限数学模型的关键步骤和一般求解过程。

［1］Blazewica J，Lenstra J K，Rinnooy Kan.Scheduling projects to resource constraints：classification and complexity ［J］.Discrete Applied Mathematics，1983，5：11.

［2］Kolisch R.Serial and Parallel Resource－constrained Project Scheduling Methods Revisited：Theory and Computation［J］.European Journal of Operational Research，1996，90（2）：320.

［3］Herroelen W，Demeulemeester E，De Reyck B，A classification scheme for project scheduling.Project Scheduling：Recent Models，Algorithms and Applications［M］.Boston／London／DordrechtL：Kluwer Academic Publishers，1999：1.

［4］Slowinski R.Two approaches to problems of resource allocation among project activities：A Comparative Study［J］.Journal of the Operational Research Society，1980（31）：711.

［5］Weglarz J.Project scheduling with discrete and continuous resources［J］.IEEE Transactions on Systems，Man and Cybernetics 1979，9，644－650.

［6］刘士新，王梦光，唐加福.一种求解资源受限工程调度问题的遗传算法［J］.系统工程学报，2002，17（1）：1.

［7］Kelley J E.The critical path method：resources planning and scheduling［C］∥Muth，Thompson，eds.Industrial Scheduling.New Jersey：Prentice－Hall，Englewood Cliffs，1963：347.

［8］Bedworth D D，Bailey JE.Integrated production control systems－management，Analysis，Design［M］.New York：Wiley，1982.

［9］Kolisch R.Serial and parallel resource－constrained project scheduling methods revisited：theory and computation［J］.European Journal of Operational Research，1996，90（2）：320.

［10］Alcaraz J，Maroto C.A robust genetic algorithm for resource allocation in project scheduling［J］.Annals of Operations Research，2001，102（1）：83.

［11］Hartmann S.A competitive genetic algorithm for resourceconstrained project scheduling［J］.Naval Research Logistics，1998，45（7）：733.

［12］Leon V J，Ramamoorthy B.Strength and adaptability of problem－space based neighborhoods for resource－constrained scheduling［J］.OR Spektrum，1995，17（23）：173.

［13］Ozdamar L.A genetic algorithm approach to a general category project scheduling problem［J］.IEEE Trans on Syst，Man and Cyber，1999，29（1）：44.