闸门调度对下游水体COD浓度衰减的敏感性分析
2013-03-15张质明王晓燕刘文竹
张质明,王晓燕,于 洋,刘文竹
(1.北京建筑大学北京应对气候变化研究和人才培养基地,北京 100044; 2.首都师范大学资源环境与旅游学院,北京 100048)
水闸的修建调度是对河流径流调控的有效途径[1]。但水闸也会破坏水系的连通性,降低水流流速,减弱自净能力,因此闸门控制对下游污染物的衰减过程会造成很大影响。我国河流闸坝多,研究闸门调度方式与下游污染物衰减过程之间的关系是水质控制管理的重要方面。
目前闸坝对水环境影响的研究大致分为两个方面:①讨论单一闸坝运行对水量水质的影响。研究方法主要利用现场实测或者根据历史数据,讨论闸坝调度对上下游水量水质的改变,进而分析闸坝对水环境的影响[2-4];②讨论闸坝群联合调度的影响。研究方法主要是借助模型对有、无闸坝的情形进行模拟,对比分析其水量、水质、生态指标变化,进而讨论闸坝的作用[5-7]。近年来,有研究基于人工神经网络模型讨论了多闸门联合调度在水文方面的影响[8],但讨论闸门调度对污染物衰减过程造成影响方面的研究并不多见。
笔者基于MATLAB R2010a软件,以北京地区北运河杨洼闸的运行状况为例,利用BP人工神经网络与一维污染物衰减模型,利用经验公式结合实地监测的方法进行参数选取,建立单一水闸多闸门调度对下游水体中COD浓度衰减影响的数学模型,并基于Sobol方法和权值分析法对模型中各参数进行敏感性分析,估算各因子对COD浓度衰减影响能力的大小。
1 资料与方法
1.1 研究区域概况与数据获取
北运河是唯一发源于北京境内的水系,来水由污水与雨洪水组成,近几年流域内降雨量减少,污水排放增加,使得河流稀释和降解能力下降,水质变差。目前整体水质为劣Ⅴ类水,其中有机污染指标COD超标严重。杨洼闸是北运河在北京界内下游的一个出境控制性拦河闸,位于平原河道,主要用于拦蓄雨洪。该闸共15孔,每孔净宽8.0 m,总宽144.0 m[9]。
选用2010—2011年北运河杨洼闸同步监测的下游处(距闸150 m处)的流量、流速、上游水位(距闸100 m处)以及开闸孔数、开闸高度、COD浓度等数据共77组样本。
1.2 模型的建立
建立耦合模型以实现闸门调度对下游河流水质变化的控制响应。在参数选择方面,通过改变下游水文、水质条件(河宽、河深、流速、COD浓度等),动态调整一般水质模型中作为常值出现的降解系数与扩散系数的数值。采用试验监测与多方法估算相结合的手段,减少因直接给定参数范围而导致参数区间过大所带来的不确定性,同时也增加了模型参数对不同水文水质条件的自适应能力。
1.2.1闸门调度与流量的响应关系
为定量研究闸门运行对水量变化的影响,笔者采用3层BP(back-propagation)神经网络模型[10]对闸门调度与流量之间的多元非线性关系进行拟合,如图1所示。

图1 神经网络模型结构
其中输入层包括上游水位H(upstream level)、开闸孔数NWG(WG Num)、开闸高度hWG(WG height)共3个神经元,输出层为流量Q(flow),并且采用提前终止法[11-12]进行样本的划分及训练。
1.2.2流量与模型参数的关系
一维水质模型在河流水质模拟中已经得到了广泛的认可[13]。假设水闸下游一定距离内为顺直河道,水体中COD污染物浓度变化则可根据一维模型进行描述:
(2)
式中:ρ为污染物质量浓度;t为时间;u为水流速度;E为弥散系数;x为河流纵向距离;S为源汇项。
a. 流量与流速关系。该断面属自然河道,河深、河宽等边界条件会随流量的不同而变化。为简便起见,采用流速与流量的监测数据进行回归分析,得到杨洼闸断面的流速与流量之间的幂指数关系为
u=0.013 3Q0.748 3
(3)
式中:Q为流量, m3/s。
Q~u回归方程的拟合效果如图2所示。

图2 Q~u线性回归趋势
由图2可知,该经验公式的误差范围较小,且均匀分布在拟合曲线两侧,拟合效果较好。
b. 降解系数KCOD的确定及修正。多项研究表明,降解系数KCOD取值与该河段的水文条件有关[14],目前已存在大量经验公式[15]。但水体中对COD的降解影响因素众多,又因各河段的特征不同,需要根据具体的河段情况进行估算[16]。笔者于2009—2010年在杨洼闸采集样品,在实验室进行样品培养,对有、无底泥与上覆水的动力条件等因素进行设定,采用德国Merck公司的NOVA60光电比色计对COD浓度进行逐日测定,得知KCOD=0.08~0.13 d-1,并随流速增加而增加。该数据与利用北京师范大学水科学研究院开发的WQS工具在北运河率定验证的结果接近(KCOD=0.1d-1)[17]。
根据试验结果表明,在河水ρ(COD)>30 mg/L时,由于底泥的吸附与释放作用达到平衡,对COD降解过程的作用并不明显;但在ρ(COD)为25~30 mg/L时,其COD释放对水质的影响开始加大,明显减缓COD降解趋势,ρ(COD)为20~25 mg/L时,达到平衡状态,浓度不再降低。因此,在COD衰减过程中加入对杨洼闸断面底泥性质的考虑,根据试验数据,对KCOD值进行如下修正:当水体中ρ(COD)<20 mg/L时,令KCOD值为零。
综上所述,KCOD值的确定方法如下:
(4)

图3 不同方法计算的纵向弥散系数随流量变化趋势及分布状况
c. 纵向弥散系数E的确定。为估计弥散系数的范围,采用多种方法[18]对杨洼闸纵向弥散系数进行估算。
图3(a)是以杨洼闸实际河道状况,利用各种方法求解弥散系数随流量变化的曲线。除Iwasa法不考虑流量变化外,其他方法所求出的纵向弥散系数均与流量变化成正比,其中Fishcer法的计算结果最大,Seo估值其次,Mcquivey法的结果最低且基本相同。如图3(b),不同方法所得的E值在5~570 m2/s之间。扩散系数同降解系数一样,均是与水力条件相关的参数,研究依照水力条件的变化,选用多种方法估算的均值进行确定,即
E均=(EMcquivey+EMcquivey2+EFishcer+ESeo+EIwasa) /5
(5)
1.3 模型敏感性分析
为定量评估水闸调度对下游水质的影响,需要对模型的参数进行全局敏感性分析。目前常见的全局敏感性分析方法包括Morris法、FAST法、Sobol法[19]、Extend FAST法、GLUE法以及基于ANN的权值分析法[20]等。
1.3.1Sobol方法
Sobol方法是目前最常用的基于方差的敏感性分析方法[21],已广泛应用于经济、环境、社会等领域大型模型中[22-23]。其原理如下。
记Ωk是将函数f(x)分解为递增项之和:
其中f(x)可用多重积分来分解,f0是个常量,其他项的任意变量积分为零,即

可以看出分解式中的各项为正交函数,也即,当(i1,i2,…,is)≠(j1,j2,…,jt),有

设f(x)总方差为D,则
偏方差可以通过唯一分解式计算得到:
其中1≤it<… 敏感度系数Si1,i2,…,is为 其中1≤it<… (6) Si叫做xi的一阶敏感性指数,用于定量描述xi在函数f(x)中所造成的影响;Si1,i2,…,is叫做因素xi1,xi2,…,xis的S阶敏感性指数,用于定量描述这S个参数共同作用对函数f(x)的影响。因此对于一个S个参数的模型来说,变量xi1总敏感性指数TSi1可以表示为 TSi1=Si1+Si1,i2+…+Si1,i2,…,is (7) Sobol方法的缺点在于各阶敏感性指数都需用蒙特卡罗积分进行计算,导致计算量较大,需要运行模型次数T为N(2m+1)次(m为参数个数,N为样本数)。特别是对于参数量较多的情况,运算时间过长。因此研究选用Sobol方法的改进算法,只需要运行模型的次数为 T=(m+2)N (8) 1.3.2ANN权值分析 由于ANN属于黑箱模型,其响应曲面的结构难以确定。若敏感性分析过程的采样量不足,则可能导致敏感性出现错误结果。故需要在进行全局敏感性分析的基础上,通过权值分析做进一步验证。 基于ANN输入变量对输出变量的贡献大小可用相对重要性指数I表示,其计算公式如下[24]: (9) 式中:wij为输入层中第i个神经元与隐层中第j个神经元之间的连接权值,r为输入元、S1为隐层神经元的个数。由于该方法是根据输入层与隐层之间的连接权值计算得出,对传递函数的形式不考虑,所以只能得到半定量的敏感度指数。但其计算过程简单,因此在ANN的敏感性分析当中应用十分广泛。 2.1.1水闸-流量模拟 根据提前终止法,训练样本为57个,测试样本为20个。根据循环语句确定出最优隐层单元个数为7,模型效果见图4。 图4 BPNN泛化及训练效果图 测试样本的模拟效果反映ANN的泛化能力;训练样本的模拟效果,反映构建模型时的训练效果。模型的最大误差出现在流量较高的时段,这是由于训练样本中高流量的数据样本不足造成的。 图5 BPNN响应曲面 由神经网络模型在归一化三维空间内的曲面中(图5)可以看出开闸高度hWG、上游水位H、开孔数量NWG这3个变量对下游流量Q的响应关系:Q与hWG、NWG均呈正相关关系,但与H关系并不明显,基本反映了杨洼闸受到频繁闸门调度控制流量的特征。 使用Nash-Suttcliffe系数Ens来衡量模拟值与观测值之间的拟合度,其表达式为 (10) 式中:Qob为观测值,Qsim为模拟值,Qob_average为观测平均值,n为观测次数。当Qob=Qsim时,Ens=1;若Ens<0,则说明模型模拟无效。在测试数据上面的模拟线性回归系数R2为0.93,Nash-Suttcliffe系数为0.84,说明泛化效果较好。 2.1.2污染物衰减过程情景模拟 水闸对流量的控制会引起污染物空间浓度分布的改变。为考虑水闸调度对污染物衰减的影响,假设水闸下游(流量受水闸控制)有一稳定输入源,污染物质量浓度为70 mg/L,排污口的排污量为3 m3/s。根据实际监测的COD质量浓度与流量的范围,进行情景设置(表1)。 表1 情景设置 不同情况下河道污染物浓度衰减过程如图6所示。 图6 不同上游来水浓度条件下的COD衰减 图6表示的是在该排污口稳态排放COD时,上述20个情景模拟的河道水质状况。可以看出,上游水质清洁时,通过调节闸门增大流量,对污染物的稀释作用明显,可以很好地改善水质状况;但是当上游水质较差时,增大流量反而会对下游水质起到污染的作用。这主要是因为增大流量的同时会引起流速增加,缩短了污染物被运移到下游河段的时间,且杨洼闸降解系数随流速变快的增幅有限,污染物来不及降解,导致水域污染面积增加。 因此在水闸调控中,应重点注意上游来水水质状况。当水质清洁时,应当尽量开闸放水。一方面有利于污染物的降解与稀释,另一方面保证了下游的用水量;而当水质较差时,应当尽量减缓放水速度,一方面以避免高浓度的污染物破坏下游水质,另一方面通过减缓河流流速,使得污染物能够在到达下游断面前得到充分降解。 2.2.1ANN权值分析结果 为了考察黑箱模型在闸门调度与下游流量的影响,可以通过计算各输入元的相对重要性指数I,结果见图7。可以看出开闸孔数对流量变化的影响最大,其次是开闸高度,上游水位的影响最小,但三者差异不大。 图7 ANN权值分析 2.2.2Sobol方法敏感性分析结果 在采样方面,纵向距离考虑长度为50 km的范围,其余各项因子均按照杨洼闸的实际范围进行采样。上游水位高度及上游来水COD浓度服从对数正态分布,其余变量均为均匀分布。 图8中是利用Sobol方法对模型各因子对入河COD浓度衰减的影响。根据中心极限定理,蒙特卡罗方法采样数量越大,敏感性指数越真实,但同时计算时间也会变长。每个因子按照其分布特征采集数量为100~1 000的样本,可以根据图8看出敏感性指数的结果在采样数为1 000时已经基本稳定。 图8 不同采样数下的各因子一阶敏感性指数与总敏感性指数变化趋势 一阶敏感性指数主要反映单个因子通过自身作用对衰减过程的影响程度,总敏感性指数主要反映各因子通过与其他因子共同作用对衰减过程产生的影响程度,总敏感性指数总是大于一阶敏感性指数。 各因子按照一阶敏感性指数的大小进行大小排序为:ρ(COD)(S=0.53),x(S=0.14),NWG(S=0.09),hWG(S=0.03),H(S=0.00)。控制流量的开闸孔数的独立影响力大于开闸高度,分析原因可能是由于较浅河道在水位变化时,开闸高度可能会超过水面而不能影响流量;两者的作用都远大于上游水位,说明水闸对流量的控制作用非常明显;这3个因子的相对重要性与ANN权值分析的结果一致;由于三者通过相互作用才能对流量进行有效的控制作用,所以单个因子所产生的方差较小。 各因子按照总敏感性指数进行大小排序为:ρ(COD)(TS=0.62),x(TS=0.21),NWG(TS=0.20),hWG(TS=0.13),H(TS=0.04)。NWG、hWG、H三者共同控制流量,因此三者的总敏感性指数与一阶敏感性指数差异较大。 由于模型中降解系数与弥散系数都依照不同的水力条件做了相应的定值处理,因此其敏感性的是通过水力条件的敏感性进行表示。由于杨洼闸断面的流速较低,弥散系数和降解系数的变化幅度并不大,通过闸门调度改变水力条件也不会显著提高两者在短距离内对河道水质的影响力。但随着所考虑的纵向距离的增加,控制流量的3个因子的作用会逐渐增强,而上游来水COD浓度的作用会有所减少。 利用人工神经网络建立水闸-流量模型,并结合修正过一维衰减模型,估算杨洼闸调度方式对下游COD浓度衰减的影响,评价模型中各参数对衰减过程的敏感度,得到以下结论: a. 利用Sobol方法与权值分析法,从方差和权值两个角度分别对水闸-流量模型进行敏感性分析,各因子之间的相对大小顺序一致; b. 通过闸门调度改变水力条件不会显著提高降解系数与扩散系数的影响力。这是由于杨洼闸断面的河道平直,弥散系数与降解系数变幅不大,并且在模型当中也结合课题组的实验结果,加入了对底泥COD释放的因素干扰; c. 综合考虑Sobol方法的一阶敏感性指数及总敏感性指数的计算结果可知,对下游COD的衰减过程具有较大影响的因子排序为:上游来水ρ(COD)(S=0.53,TS=0.62),纵向距离x(S=0.14,TS=0.21),水闸开孔数NWG(S=0.09,TS=0.20),开闸高度hWG(S=0.03,TS=0.13)。 [ 1 ] 鲍全盛,王华东,海热提.沙颖河闸坝调控与淮河干流水质风险管理[J].上海环境科学,1997,4(16):11-14(BAO Quansheng,WANG Huadong,HAI Reti.Preliminary study on the sluice gate regulation of Shayinghe river and risk management of water quality in Huaihe trunk stream[J].Shanghai Environmental Sciences,1997,4(16):11-14.(in Chinese)) [ 2 ] 郭文献,张亮,王鸿翔,等.闸坝工程建设对北运河水量水质影响研究[J].灌溉排水学报,2010,29(6):56-59(GUO Wenxian,ZHANG Liang,WANG Hongxiang,et al.Effects of dams and floodgates on river flow regimes and water quality of Beiyun river[J].Journal of Irrigation and Drainage,2010,29(6):56-59.(in Chinese)) [ 3 ] 郑保强,窦明,左其亭,等.闸坝调度对水质改善的可调性研究[J].水利水电技术,2011,42(7):28-31(ZHENG Baoqiang,DOU Ming,ZUO Qiting,et al.Research on adjustability of water quality improvement from operation dispatch of sluice and dam[J].Water Resources and Hydropower Engineering,2011,42(7):28-31.(in Chinese)) [ 4 ] 刘子辉,左其亭,赵国军,等.闸坝调度对污染河流水质影响的实验研究[J].水资源与水工程学报,2011,22(5):34-37(LIU Zihui,ZUO Qiting,ZHAO Guojun,et al.Experiment of impacts of gate dispatching onwater quality of polluted river[J].Journal of Water Resources & Water Engineering,2011,22(5):34-37.(in Chinese)) [ 5 ] 张永勇,陈军锋,夏军,等.温榆河流域闸坝群对河流水量水质影响分析[J].自然资源学报,2009,24(10):1697-1705(ZHANG Yongyong,CHEN Junfeng,XIA Jun,et al.Research on the impact of dams and floodgates on riverine runoff and water quality in Wenyu River Basin[J].Journal of Natural Resources,2009,24(10):1697-1705.(in Chinese)) [ 6 ] 张永勇,夏军,王纲胜,等.淮河流域闸坝联合调度对河流水质影响分析[J].武汉大学学报:工学版,2007,40(4):31-35(ZHANG Yongyong,XIA Jun,WANG Gangsheng,et al.Research on influence of dams’union dispatch onwater quality in Huaihe River Basin[J].Engineering Journal of Wuhan University,2007,40(4):31-35.(in Chinese)) [ 7 ] 夏军,赵长森,刘敏,等.淮河闸坝对河流生态影响评价研究:以蚌埠闸为例[J].自然资源学报,2008,23(1):48-60(XIA Jun,ZHAO Changsen,LIU Min,et al.Impact assessment of dams and flood gates projects of Huaihe River on river ecosystem:a case study of the Bengbu site[J].Journal of Natural Resources,2008,23(1):48-60.(in Chinese)) [ 8 ] 郑毅,方红卫,何国建,等.基于径向基函数的多闸门控制河流的洪水模拟[J].清华大学学报:自然科学版,2008,48(12):2061-2064(ZHENG Yi,FANG Hongwei,HE Guojian,et al.Flood simulations using radial basis functions for complex river flows controlled by sluice [J].Journal of Tsinghua University:Natural Science,2008,48(12):2061-2064.(in Chinese)) [ 9 ] 杨淑慧,王理许,张霓,等.北运河杨洼闸泄流能力试验研究[J].北京水务,2006(4):31-34.(YANG Shuhui,WANG Lixu,ZHANG Ni,et al.Experiment of flood carrying capacity of Yangwa water gate in Beiyunhe river[J].Beijing Water,2006(4):31-34.(in Chinese)) [10] GEMAN S,BIENENSTOCK E,DOURSAT R.Neural networks and Bias/Variance dilemma[J].Neural Computation,1992,4:1-58. [11] CATALTEPE Z,ABU-MOSTAFA Y S,MAGDON I M.No free lunch for stopping [J].Neural Computation,1999,11:995-1009. [12] 陈柳,马广大.大气中SO2浓度的小波分析及神经网络预测[J].环境科学学报,2006,26(9):1553-1558.(CHEN Liu,MA Guangda.Study on wavelet analysis and neural network prediction of SO2concentration in air[J].Acta Scientiae Circumstantiae,2006,26(9):1553-1558.(in Chinese)) [13] 罗固源,郑剑峰,许晓毅,等.基于遗传算法的次级河流回水段水质模型多参数识别[J].中国环境科学,2009,29(9):962-966.(LUO Guyuan,ZHENG Jianfeng,XU Xiaoyi,et al.Parameters identification of water quality model in branch backwater reach based on genetic algorithm[J].China Environmental Science,2009,29(9):962-966.(in Chinese)) [14] 王美敬,罗麟,程香菊,等.紊动对有机物降解影响研究[J].武汉大学学报:工学版,2005,38(4):1-4(WANG Meijing,LUO Lin,CHENG Xiangju,et al.Study of effect of turbulence on organic compound biodegradation[J].Journal of Wuhan University of Hydraulic and Electric Engineering,2005,38(4):1-4.(in Chinese)) [15] WRIGHT R M,MEDONELL A J.In-stream de-oxygenation rate prediction [J].Proc ASCE J Env,1979,105(4):323-335. [16] COX B A.A review of currently available in-stream water-quality models andtheir applicability for simulating dissolved oxygen in lowlandrivers[J].The Science of the Total Environment,2003,314:335-377. [17] 郭云慧,李红华,鱼京善.北京市通州区水环境规划方案下的水质模拟研究[J].北京师范大学学报:自然科学版,2009,45(5):654-657.(GUO Yunhui,LI Honghua,YU Jingshan.Water quality simulation under the environmental management scheme in Tongzhou District,Beijing[J].Journal of Beijing Normal University:Natural Science,2009,45(5):654-657.(in Chinese)) [18] 师鹏飞.渭河关中段水质水量响应关系分析研究[D].西安:西安理工大学,2010. [19] SOBOL I M.Sensitivity estimates for non-linear mathematical models[J].Mathematical Modelling and Computational Experiment,1993,4(1):407-414. [20] 蔡毅,邢岩,胡丹.敏感性分析综述[J].北京师范大学学报:自然科学版,2008,44(1):9-16(CAI Yi,XING Yan,HU Dan.On sensitivity analysis[J].Journal of Beijing Normal University:Natural Science,2008,44(1):9-16.(in Chinese)) [21] MARA T A ,TARANTOLA S.Variance-based sensitivity indices for models with dependent inputs[J].Reliability Engineering and System Safety,2012,107:115-121. [22] YANG J.Convergence and uncertainty analyses in Monte-Carlo based sensitivity analysis[J].Environmental Modelling & Software,2011,26:444-457. [23] DIMOV I,GEORGIEVA R,IVANSOVSKA S,et al.Studying the sensitivity of pollutants’ concentrations caused by variations of chemical rates[J].Journal of Computational and Applied Mathematics,2010,235:391-402. [24] LEE J H W,HUANG Y,DICKMAN M,et al.Neural network modelling of coastal algal blooms[J].Ecological Modelling,2003,159:179-201.2 结果与讨论
2.1 模型模拟
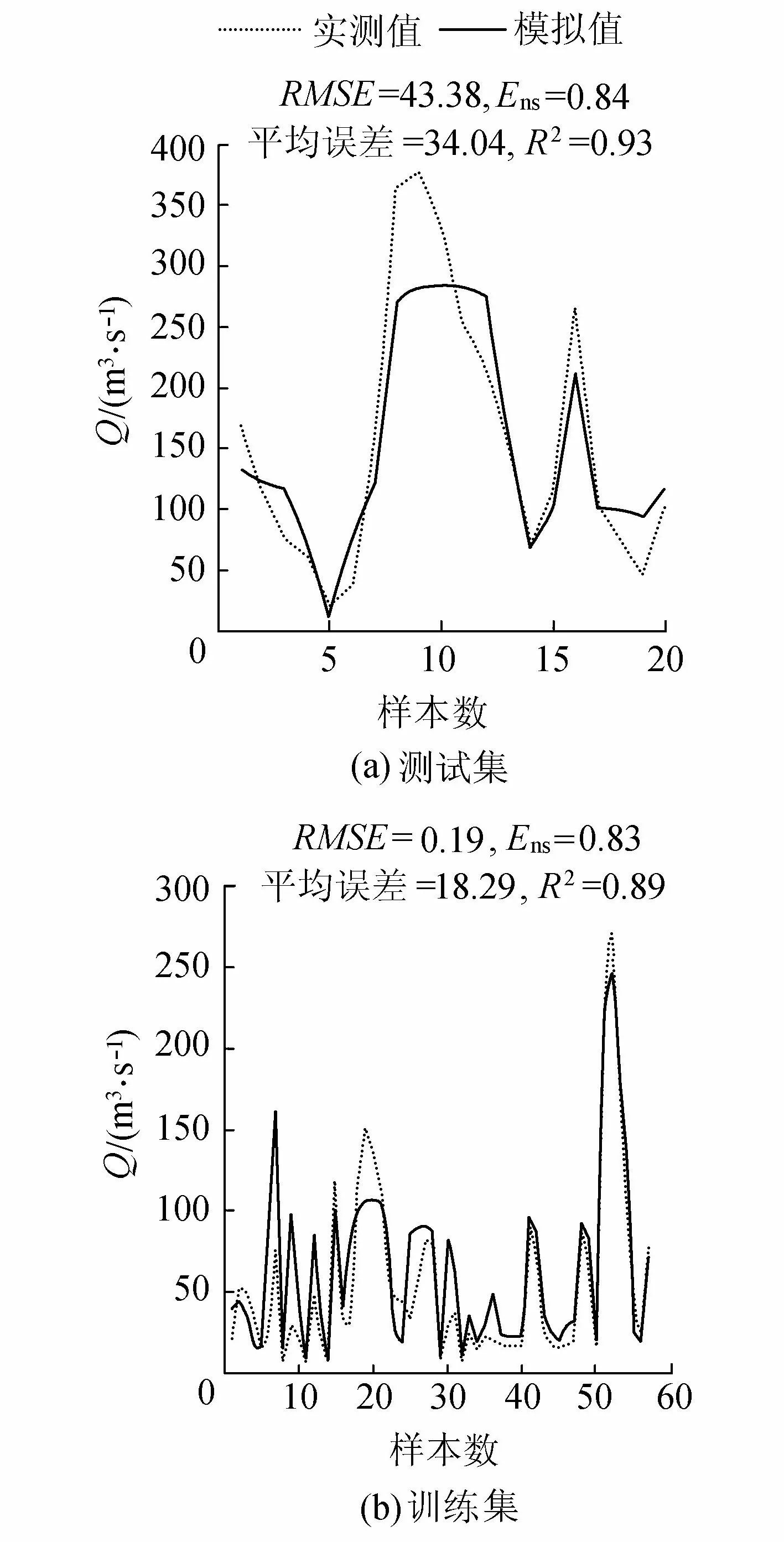



2.2 模型敏感性分析


3 结 论
