电力系统无功优化算法性能比较及分析

周文俊，吴 熙 ，施伟成

(1.镇江供电公司调度控制中心，江苏镇江212000；2.东南大学电气工程学院，江苏南京210096)

电力系统无功优化是保证系统安全经济运行的有效手段，是提高电力系统电压质量的重要措施之一。所谓无功优化，就是指在系统的结构参数及负荷情况给定、无功电源较为充裕的情况下，通过调节发电机机端电压或出力、调整变压器抽头变比、改变无功补偿装置的出力等措施来调整无功潮流，在满足所有指定约束条件的前提下，使系统的某一个或多个性能指标达到最优时的无功调节手段。通过无功优化不仅使全网电压在额定值附近运行，且能取得可观的经济效益，使电能质量、系统运行的安全性和经济性完美的结合在一起，因而无功优化的前景十分广阔[1-3]。

1数学模型

1.1无功优化模型

无功优化通常的数学描述为：

式（1）中：u为控制变量，是人为可调节的变量，通常可取发电机端电压、可调变压器的抽头位置和节点装设无功补偿设备的补偿容量；x为状态变量，包括除发电机节点和平衡节点外所有节点的电压、发电机无功出力和线路无功功率；f（u，x）为无功优化的目标函数，本文取最小网损；h（u，x）为等式约束条件，即节点潮流方程；g（u，x）为控制变量与状态变量须满足的约束条件。

1.2算例模型及控制变量

本文以IEEE30节点标准系统为例进行研究，IEEE30节点标准测试系统结构如图1所示。图1中，含6台发电机和4台可调变压器；2个无功补偿节点。取节点l为系统平衡节点，节点10，24安装无功补偿设备，每组并联补偿装置中有电容器2 Mvar×16组，电抗器为-2Mvar×8 组;支路 4-12，6-9，6-10，28-27为有载可调变压器支路，变压器最大变比1.1，最小0.9，分接头数目为16个。控制变量对应为发电机的机端电压、4台可调变压器的变比K及2台无功装置的补偿电纳值。状态变量x则为发电机的无功出力和所有PQ节点电压。

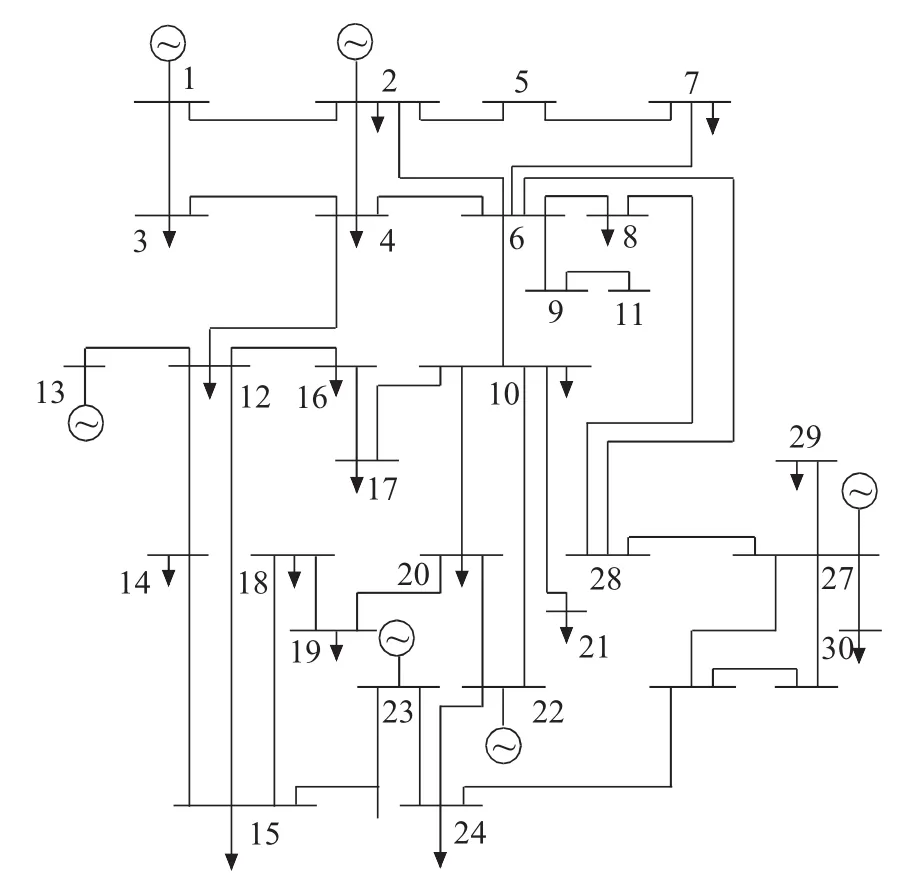
图1待研系统

2基于序列二次规划的非线性规划法

二次规划法将目标函数作为二阶泰勒级数展开，把非线性约束转化为一系列线性约束，构成二次规划优化模型，从而通过多次二次规划来逼近最优解[4]。即：

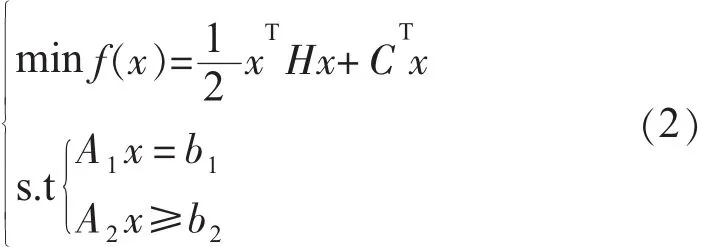
在matlab中，可用fmincon函数求多变量有约束非线性函数的最小值。fmincon运行时首先检查有无梯度表达提供，如有则选择大规模算法，如果没有梯度表达式提供，fmincon选择序列二次规划（SQP）算法。需要

式（3）中：fmax为上代群体最优适应值；favr为上代群体平均适应值；fc为要交叉的两串中较大适应值。指出的是，该算法仅能用于控制变量为连续变量的优化，优化的最后结果必须进行离散化。二次规划法计算结果统计如表1所示，计算得到有功网损最小值为1.980 8 p.u.。在此取进行离散化后的最小有功网损1.982 6 p.u.。

表1二次规划法优化结果

3改进遗传算法

遗传算法是由美国学者Holland提出的一种基于达尔文生物进化论及门德尔基因遗传理论的仿生学概率性迭代搜索算法，同时也是一种组合优化算法。其最大特点就是不依赖函数性质，对函数是否连续，是否能求二阶导数没有要求，非常适合求解非线性规划问题。该方法主要包括编码、控制参数、适应值函数、遗传算子（交叉及变异）、选择及终止条件。 遗传算法虽在复杂的工程优化问题中得到了广泛应用[2，5，6]，但由于算法随机搜索而带来的算法收敛速度慢及计算稳定性差已成为其应用的最大阻碍。为了改善算法的性能，已对其进行了大量研究，提出了不少改进方法。为了弥补遗传算法在工程应用上的不足，本文针对无功优化问题采用了一种改进的遗传算法。

3.1混合编码方式

IEEE30节点系统总共有12个控制量，其中包括6个连续可调的发电机端电压，2个离散可调的无功补偿和4个离散可调的变压器变比。发电机端电压采用实数编码，直接表示机端电压；其他两种离散变量采用整数编码，通过对定义数组的搜索得到其对应实际值。

3.2优选父代自适应交叉操作

借助优生学原理，该操作在进行交叉操作时，提高被交叉父代个体的质量，以期望产生高质量的子代。具体操作是从上代群体中随机选择2个个体，保留适应值大的个体(如二者适应值相同，则随机保留一个)，再进行一次上述两两优选操作。对保留下来的2个个体进行交叉。为了保证交叉质量，交叉概率采用自适应方式产生，即交叉概率由进化程度来控制。自适应交叉概率为：

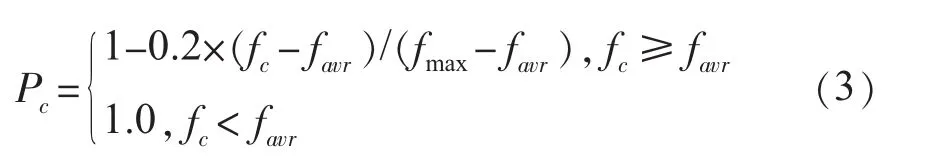
3.3非一致自适应变异操作

变异算子保证算法能搜索到解空间中的每一点，使算法具有全局收敛性。使用实数编码时，变异算子不再像二进制编码时仅是简单的恢复群体的多样性，它已成了一个重要的搜索算子。变异对经过优选交叉的个体进行，具体采用实数编码的非一致变异方式。该算子的结果同进化代数密切相关，使得在进化初期，变异范围相对较大，而随着进化代数的推进,变异范围越来越小，起一种对进化系统微调的作用。

3.4产生新种群

将原种群和杂交变异生成的新种群依照网损最小原则进行排序，并去处相同的个体。考虑到目标函数计算时，加入了罚函数，单纯依照网损最小原则选择前30%的个体会照成种群多样性的下降，出现“早熟”。而且对于状态量越界的个体，某几位变异后可能得到更优解，所以不能单纯的排除这些越界个体。为了解决这个问题，采用了保留网损最小的个体 （也就是最优个体），对其他个体采用平均概率法选择出其中的剩余新父代个体的方法。这样既保证了遗传算法的收敛性，也尽可能的保证了父代种群的多样性，有利于避免过早收敛的问题。初始种群为30个个体，交杂生成40个新个体，变异生成60个新个体，将这130个个体放在匹配池。首先保留最优个体，再在剩下的个体中选择出另外29个个体作为新的父代。最大迭代次数为100次，当十次迭代最优值不变时，则认为计算收敛，输出最优个体的控制参数和网损。改进遗传算法流程图如图2所示。改进遗传算法计算结果统计如表2所示。

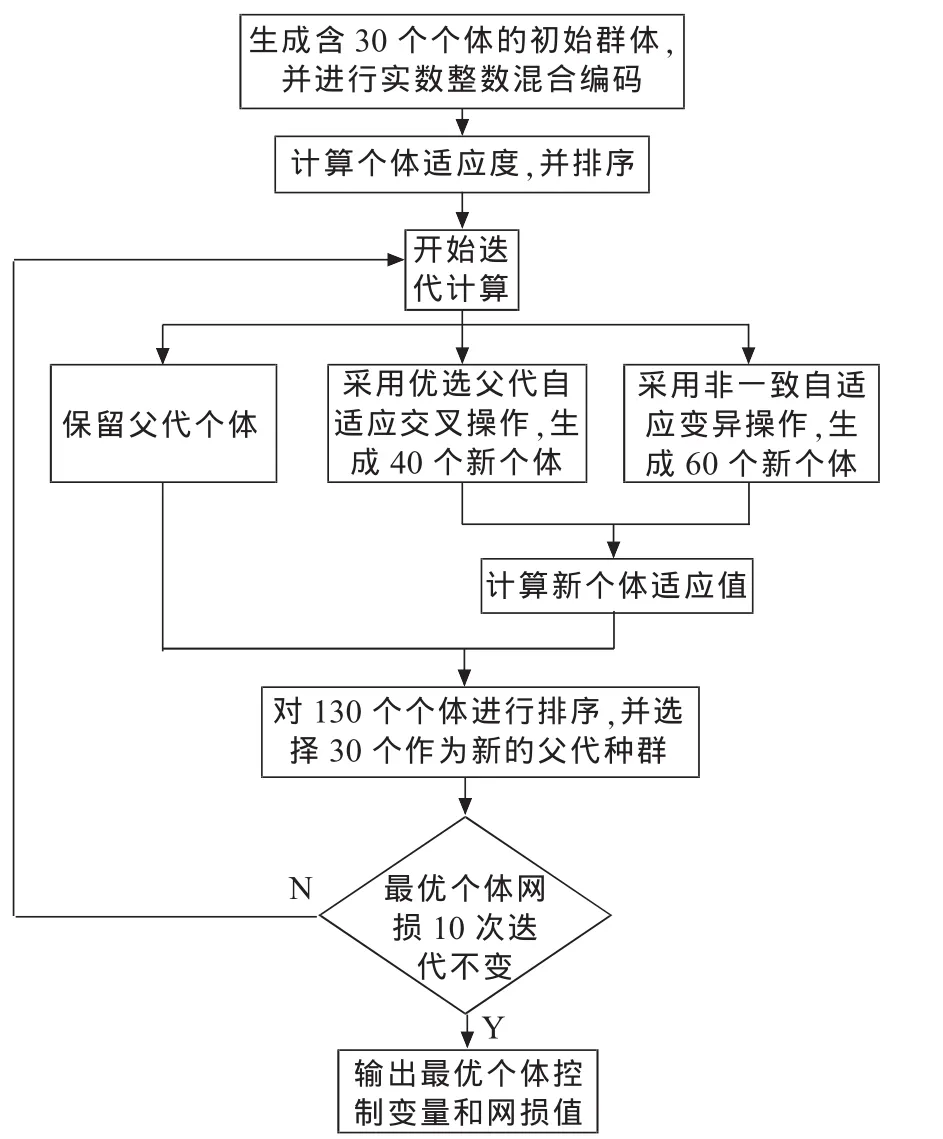
图2改进遗传算法流程图

表2改进遗传算法优化结果

4改进粒子群算法

粒子群算法[7-9]是1995年由美国社会心理学家James Kennedy和电气工程师Russell Eberhart共同提出，其基本思想是受他们早期对鸟类群体行为研究结果的启发，并利用生物学家Frank Heppner的生物群体模型。粒子群算法与其他进化类算法相类似，也采用“群体”与“进化”的概念，同样也是依据个体（粒子）的适应值大小进行操作。所不同的是粒子群算法不像其他进化算法那样对于个体使用进化算子，而是将每个个体看作是在n维搜索空间中的一个没有重量和体积的粒子，并在搜索空间中以一定的速度飞行。该飞行速度由个体的飞行经验和群体的飞行经验进行动态调整。 设 Xi=（xi1，xi2，…，xin）为粒子 i的当前位置；Vi=（vi1，vi2，…，vin）为粒子 i的当前飞行速度；Pi=（pi1，pi2，…，pin）为粒子 i所经历的最好位置，也就是粒子i所经历过的具有最好适应值的位置，称为个体最好位置。对于最小化问题，目标函数值越小，对应的适应值越好。Pg为所有粒子经过的最好位置。基本粒子群算法的进化方程可描述为：式（4）中：下标“j”为粒子的第 j维；“i” 为粒子 i；t为第t代；c1，c2为加速常数， 通常在 0～2 间取值；r1，r2为 2个相互独立的0到1之间的随机数。为了减少在进化过程中，粒子离开搜索空间的可能性，vij通常限定于一定范围内。

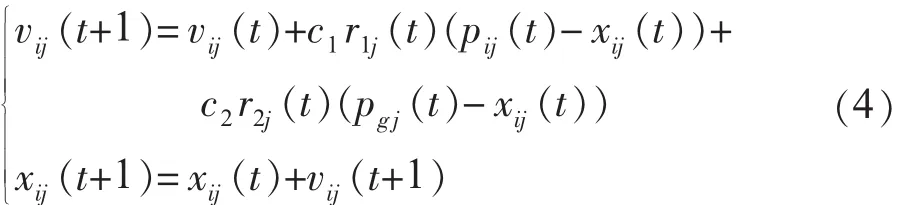
对于不同的问题，如何确定局部搜索能力与全局搜索能力的比例关系，对于其求解过程非常重要。甚至对于同一个问题而言，进化过程中也要求不同的比例。为此，Yuhui Shi 1998年提出了带有惯性权重的改进粒子群算法[8，9]。 其进化方程为：

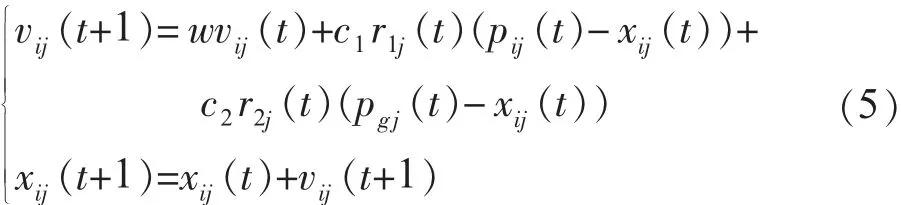
进化过程中动态调整惯性权重以平衡收敛的全局性和收敛速度：

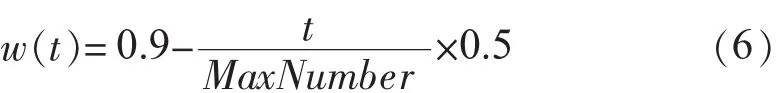
其中，MaxNumber为最大截止代数。这样，将惯性权重看作迭代次数的函数，可从0.9到0.4线性减少。改进粒子群算法的流程如图3所示。其计算结果统计如表3所示，且结果表明粒子群法收敛速度快，收敛点相对稳定，较其他算法表现出更多的优良特性。

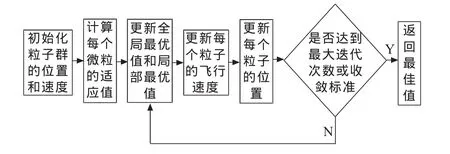
图3改进粒子群算法流程图

表3改进粒子群算法优化结果

5算法比较

各种不同算法的结果汇总如表4所示。

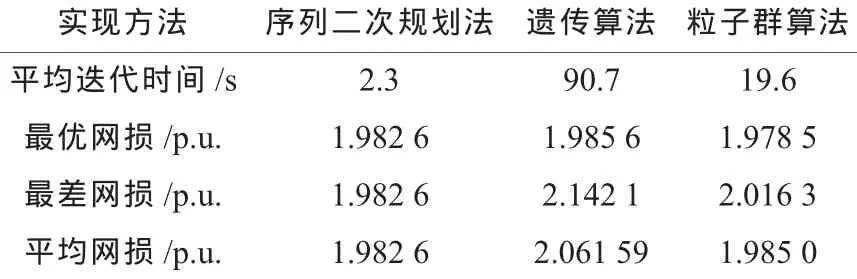
表4优化结果汇总

通过以上结果来看，序列二次规划法、和粒子群算法所得的结果最优，在同时处理连续变量的情况下，PSO算法的平均值没有二次规划法好，但最优值比二次规划法略好。由于实际的电力系统中无功补偿容量和变压器变比是离散变量，因此将所得结果离散化后再和直接处理离散变量的PSO算法相比较，发现PSO算法更优。PSO算法也存在一些弱势，比如算法还不够稳定，不是每次所得结果都能收敛到一个点，但总体来每次结果相差很小。二次规划法是传统优化方法，具有稳定性好，局部寻优能力强的等特点，而粒子群法属于现代算法，具有对目标函数要求低，能可靠地收敛到较优解等特点。

遗传算法和粒子群法同属进化算法，但PSO算法在进化过程中同时保留和利用位置与速度 （即位置的变化程度）信息，而遗传算法仅保留和利用位置的信息。 如果将 xij（t+1）=xij（t）+vij（t+1）看作一个变异，则PSO算法与进化规划很相似。所不同之处在于，在每一代，PSO算法中的每个粒子只朝一些根据群体的经验认为是好的方向飞行，而在进化规划中可通过一个随机函数变异到任何方向。也就是说，PSO算法执行一种有“意识”的变异。从理论上讲，进化规划具有更多的机会在优化点附近开发，而PSO则有更多的机会更快地飞到更好解的区域，如果“意识”能提供有用的信息。

总体来说，从理论上讲粒子群算法比遗传算法要表现出更多的优良特性，但在优化领域中，有一个值得一提的著名理论，“No Free Lunch Theorems for Optimization”，即无免费午餐定理。在这2种算法的比较中也有所体现，PSO算法虽然能得到较好的结果，全局搜索能力强，但其局部搜索能力就相对较差，若用两次最优解不变作为算法的收敛条件，很容易就会返回一个较差的解，因为在搜索到较好解区域后，其局部搜索能力较差，往往会连续几次都不能找到更好的解，但遗传算法的局部搜索性能就相对较好，往往能很快在小区域内搜索到最优解，不过遗传算法往往更容易陷入局部最优解，因为其变异是没有方向的，寻到更好解区域的概率较小。另外，对于这2种算法本身，无免费午餐定理也有一定体现，首先看遗传算法，在遗传算法中，父代基因的保留个数和变异杂交概率率是此算法中最重要的两个量，父代基因保留得越全变异杂交率越小，则越容易收敛到局部最优解。反之则越难收敛，最极限的情况就是将变异概率置为无穷，不保留父代基因，则该算法就等同于随机搜索。粒子群算法也一样惯性权重取得越大，则越容易搜索到全局最优解，搜索速度最慢，反之取得越小，局部搜索能力越强，越容易收敛。理论上可以通过调节速度因子来使PSO算法的搜索能力更强，但这种调节是非常难做到的，目前位置并没有统一的调节方案，Yuhui Shi的调节方法也仅仅是一种指导性的方案，对于不同的对象，惯性权重的取法是很有讲究的，因为很难确定是否已经进入了全局最优解区域，若过早将惯性权重调小，则容易收敛到局部解，若惯性权重过大，则粒子每次位置变动过大，不但局部搜索能力变差，还很容易越界。

6结束语

本文分析了3种常用的优化方法在解决电力系统无功优化问题时的优劣性。结果表明序列二次规划法属于传统算法，收敛性和稳定性非常好，每次都收敛到同一个点，且速度较快。遗传算法和粒子群算法属于现代搜索算法，对原函数要求低，搜索能力强，但稳定性和速度不如序列二次规划法。遗传算法比粒子群算法的局部收敛能力强，但更容易收敛到局部最优解，而粒子群全局搜索能力强，但局部搜索能力不如遗传算法。总体来说，这3种算法中粒子群算法最优，它能处理离散变量，计算速度较快，并且优化所得到的结果最好。

[1]王锡凡，方万良，杜正春.现代电力系统分析[M].北京：科学出版社，2004.

[2]熊信银，吴耀武.遗传算法及其在电力系统中的应用[M].北京：华中科技大学出版社，2002.

[3]赵 波，曹一家.电力系统无功优化的多智能体粒子群优化算法[J].中国电机工程学报，2005(5)：1-7.

[4]刘桂龙，王维庆，张新燕，等.无功优化算法综述[J].电力学报，2010，25(5)：372-376.

[5]郏宣耀，王 芳.一种改进的小生境遗传算法[J].重庆邮电学院学报(自然科学版)，2005，17(6)：721-723.

[6]周双喜，杨 彬.影响遗传算法性能的因素及改进措施[J]，电力系统自动化，1996，20(7)：24-26.

[7]KENNEDY J,EBERHART R C.Particle Swarm Optimization[C].Proc.IEEE Int'l.Conf.on Neural Networks.Piscataway,1942-1948.

[8]SHI Y,EBERHART R C.A Modified Particle Swarm Optimizer[C].IEEE Press.Proceedings of the IEEE International Conference on Evolutionary Computation.Piscataway,1998：69-73.

[9]SHI Y,EBERHART R C.Empirical Study of Particle Swarm Optimization[C].IEEE Service Center.Proceedings of the 1999 Congress on Evolutionary Computation.Piscataway,1999：1945-1950.