基于遗传算法的风险偏好系数均值方差拓展模型

张 群，张 超，黄晓霞，应海瑶

（北京科技大学 东凌经济管理学院，北京 100083）

0 引言

Markowitz证券组合投资模型理论是解决证券投资最优策略问题的奠基性研究成果[1]，证券的组合投资风险是为了实现风险一定情况下收益最大化或是收益一定情况下风险最小化，即投资者的组合投资策略在风险和收益的有效前沿处取得。但该模型忽略了投资实践中的一些重要因素，如只考虑无摩擦市场而勿略了在交易过程中产生的交易费用，假设证券的数目是无限且连续可分的，这些条件在现实市场中难以满足，因此缺乏实用性。不少学者对该经典模型进行拓展研究，取得了一些研究成果。文献[2]-[4]考虑了在现实交易过程中产生的交易成本，构建了相应的模型。文献[5]-[7]等考虑了最小交易批量和最大证券持有量，并构造出求解此类问题的一种启发式算法。Hamid Reza Golmakani对Markowitz均值方差模型加入了四个限制条件[8]：持有的资金限制，最小交易批量限制，区域资金分散限制，证券数量限制。该论文首次提出了区域分散对模型的影响。张莉,唐万生讨论了概率准则下投资组合模型[9]，并研究了中国目前证券市场的整手股票交易和限制买空卖空的要求对模型解的影响。为了求解该整数规划模型，作者基于遗传算法，设计出了相对应的求解方法并在MATLAB中实现了模型算法。利用实例证实了该遗传算法求解这类模型的有效性和可行性。这些文献分别考虑了交易过程中的交易成本和最小交易批量限制等现实因素，但未将这两个因素同时考虑到模型中，并且在模型构建过程中并没有考虑投资者自己的风险偏好及不同风险偏好投资者对投资策略的影响。基于此，本文引入风险偏好系数的概念，并同时考虑交易成本、资金约束、最小交易批量等限制条件，构建了风险偏好系数均值方差拓展模型。并针对该模型的具体形式，给出了遗传算法的具体实现过程。

1 投资组合模型

Markowitz于1952年首次从规范经济学的角度揭示了如何通过建立证券组合的有效边界来选择最优证券组合，并分析了如何通过分散投资来降低风险,开创了现代投资组合理论的先河。其核心思想是证券的组合投资是为了实现风险一定情况下收益最大化或收益一定情况下风险最小化，具有降低证券投资活动风险的机制。Markowitz在基于一系列假设条件下，得到了经典的均值方差模型。这些假设条件包括：

(1)投资者进行交易的证券市场是强势有效的，证券价格反映了证券的内在价值，任何价格的波动都会体现在价格上，且每个投资者都掌握相同的充分信息，了解每种证券的期望收益率及其标准差。

(2)证券投资者以期望收益率来衡量未来收益的水平，以期望收益率的方差来衡量收益率的波动情况，并以这两个指标作为选择投资方案的依据。

(3)投资者做出的依据标准是：期望收益率一定的情况下，风险最小；风险一定的情况下，收益最高。

(4)各种证券的收益率服从正态分布，且证券之间有一定的相关性，可用收益率之间的协方差来表示，投资组合的风险即为组合中的协方差乘以权重求和。

(5)每一项资产都是无限可分的，这意味着，如果投资者愿意的话，他可以购买一个股份的一部分。

(6)投资者可以以一个无风险利率贷出(即投资)或借入任意资金。

(7)交易市场是无摩擦的，意味着税收和交易成本均可忽略不计，尽管这在现实操作过程中难以实现。

根据上述假设，Markowitz得到均值方差模型的基本形式为：

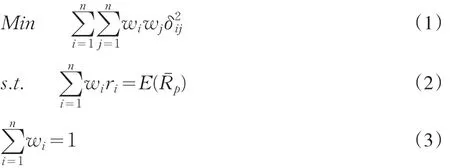
其中：δij为第i种证券和第 j种证券的协方差，E(RˉP)为投资组合的期望收益率，wi为第i种证券的投资权重，ri为第i种证券的期望收益率。

模型利用证券的协方差来度量证券的组合风险，目标函数为投资组合的风险最小化。约束（2）为投资组合收益率需达到预先给定的期望收益率。

Markowitz均值方差模型认为投资者做出的依据标准是：期望收益率一定的情况下，风险最小；风险一定的情况下，收益最高。但在实际操作过程中，投资者个人对风险资产的态度,是影响投资者风险投资决策的主观因素，通常用效用函数表示，虽然效用函数概念清晰，但是实用性不高。苏为华等根据证券市场中的投资者对待风险有不同的态度[10]，提出了风险偏好系数的概念。风险系数为投资者在不同的有效收益，风险组合之间做出抉择提供了依据。基于风险系数提出的均值方差模型为：

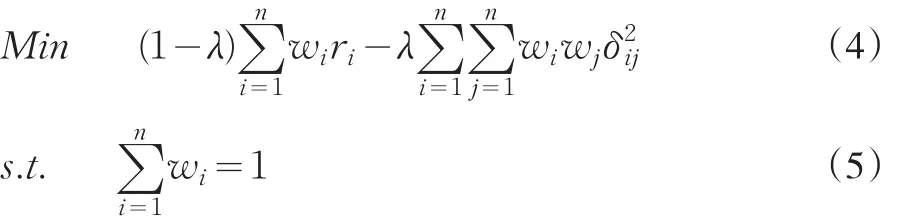
其中：δij为第i种证券和第 j种证券的协方差，wi为第i种证券的投资权重，ri为第i种证券的期望收益率，λ为投资者的个人风险偏好系数，介于0和1之间。λ的取值越大，表明投资者越厌恶风险，λ的取值越小，表明投资者越喜好风险。当λ为1时，投资者极端厌恶风险，组合的收益率取值对决策无影响，唯一目标是使得投资组合的风险最小。当λ为0时，投资者极端喜好风险，组合的收益率是唯一对决策有影响的因素，无论投资组合的风险的取值为多少，这两种为极端情况。一般投资者的风险偏好系数大于0，而小于1。投资者在确定的风险偏好下，在不同的收益，风险组合之间抉择，从而达到组合值的最大化。

2 风险偏好系数均值方差拓展模型

经典Markowitz的均值方差理论为了达到简化的目的，很多条件都做了理想化的处理。首先模型没有考虑买进卖出所产生的费用，但在现实市场买卖证券过程中，存在印花税、过户费、佣金、等其他费用，不可避免的交易成本会对收益产生影响，不考虑交易费用的模型往往导致无效的投资组合。在研究过程中，交易函数的表现形式主要有三种常用的交易费用函数，分别是反S交易费用函数，折线型费用函数以及V型交易费用函数。本文模型认为无风险资产的买卖不收取交易费用，而风险证券买卖则收取一定的交易费用。风险证券的交易成本函数为：买入单位风险证券的交易成本为买入价格的a倍，卖出单位风险证券的交易成本为卖出价格的b倍。因而在该交易成本下的第i种证券实际收益率为：

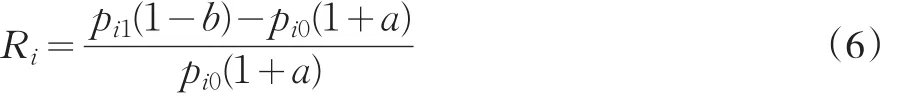
则对某一投资组合的方差为：

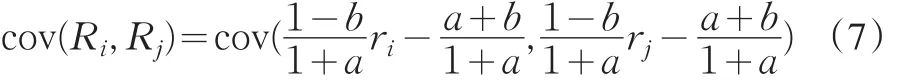
假设投资者将资金投资在风险资产和无风险资产上。根据风险偏好系数均值方差模型，考虑交易成本建立的风险偏好系数均值方差模型如下：

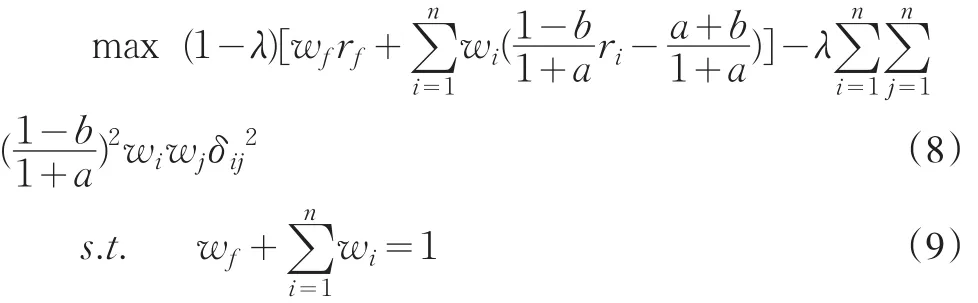
其中：δij为第i种证券和第 j种证券的协方差，wi为第i种证券的投资权重，ri为第i种证券的期望收益率，λ为投资者的个人风险偏好系数，wf为无风险资产收益率，rf为无风险资产的投资权重。

式（8）中单只证券的收益率不再是资本的股价变化率，而是考虑了交易成本的收益率。式（9）表示投入在风险证券和无风险证券权重之和为1，意味着所有资金分配到风险证券和无风险证券上。

传统的均值方差模型的另一个假设为所有证券无限可分，投资在每只证券上股数可以是任意正数。在这样的假设前提下，投资在每只证券上的股数和权重是连续的，对应的有效前沿是一条连续无间断的曲线。但在实际交易过程中，每个国家都是以整数股进行交易的，且有最小交易单位。例如我国证券市场规定A股的最小交易单位为一手，即100股，每次交易量必须是一手的整数倍。因此资产无限可分的近似程度有可能导致很大的误差，使得投资者无法达到预先设定的投资目标，甚至带来损失。因此，将最小成交批量的限制考虑到模型当中，有很强的现实意义。

最小交易单位限制条件的构建过程为：qi表示第i种风险证券要求交易的最小单位，pi0为第i种证券在决策时点的价格，xi为购买的第i种风险证券的最小单位倍数，则qixi为购买的第i种风险证券的在总数量，其中xi为整数。对于无风险证券，则无最小交易批量的限制。

对于投资者而言，由于筹集到的资金有限，投资在风险证券上的资金也会受到限制。因此，投资者在进行实际投资时会受到投资资金总额的限制。假设B为资金总额的限制，意味着投资在风险证券和无风险证券上的资金总额必须小于或者等于B。除去资金总额的限制约束，投资者有可能会为每只证券设定持有股数的上下限（bounds on holdings）或者投入资金的上下限，从而达到尽可能的分散风险的目的。甚至有些投资者会根据自身预期，需要与偏好，也会对不同股票的投资金额设定一个范围。

则投资组合的期望收益率可以表示为：

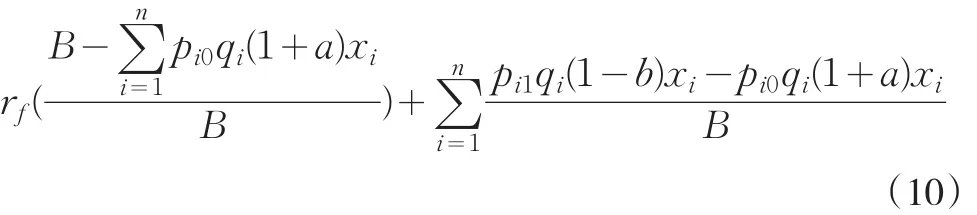
该式的前半部分表示无风险证券的收益率，后半部分表示风险证券的组合收益率，相加得到含有风险证券和无风险证券的组合收益率。投资组合的方差为：

综上所述，得到风险偏好系数均值方差模型的拓展形式如下：

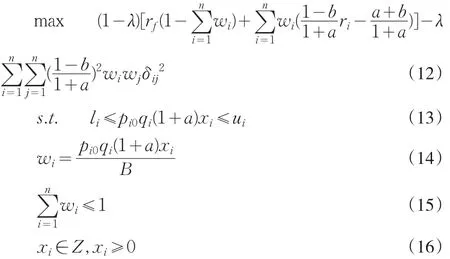
其中：λ为投资者的个人风险偏好系数，rf为无风险资产的投资权重，wi为第i种证券的投资权重，a为买入股票时的交易成本费率，b为卖出股票时的交易成本费率，ri为第i种证券的期望收益率，δij为第i种证券和第j种证券的协方差，li为第i种证券要求的投资最低额的限制，ui为第i种证券要求的投资最高额的限制，pi0为第i种证券在决策时点的价格，qi为第i种证券要求的最小交易批量，B为资金总额的限制，xi为投资于第i支股票的批量数，我国股市要求最小交易批量单位为“手”（100股），因此xi为大于0的整数。

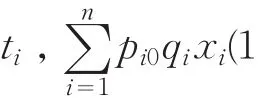
3 求解模型的遗传算法设计

由于得到的模型是一个非线性整数规划问题，而且一般备选股票规模都较大（25--2000），用传统分支定界等方法无法对该问题求解，如文献[11]研究了带有最小交易量限制的投资组合问题，但根据传统算法得到的最优解不是整数，无法满足模型的全部约束条件。因此，对本模型只能通过一些启发式算法进行求解。遗传算法（Genetic Algorithms，GA）以达尔文的进化论作为依据，模拟自然界的生物进化过程，通过优胜劣汰最终获得最优的结果。最近十几年遗传算法得到了很大的发展和广泛的应用，遗传算法具有很强的稳健性和很高的效率，可以以较大的概率得到全局最优解。传统遗传算法只能求解无约束优化问题，为了对本模型进行求解，需要对遗传算法进行设计。设计遗传算法的总体思路是：采用整数编码方案进行编码，每个基因位对应备选股票，同时基因位的值表示当前方案中投资备选股票的批量数，在染色体生成过程中将染色体的基因位数值限制在约束（13）范围内。对每一个染色体，判断其是否满足约束（15），如果不满足则随机选择一个基因位进行调整，调整后再进行判断，以此循环，直到满足约束条件。遗传操作中交叉操作和变异操作均采用双点操作，选择操作则采用轮盘赌方法来进行。遗传算法的具体实现过程如下：

（1）编码

采用整数编码，每个染色体含n个基因位(代表n只证券)，基因的数值代表投资于该证券的总手数。并且每个基因位取值都满足约束（13）限制的范围。即编码为{x1,x2,…,xn}且li≤pi0qi(1+a)xi≤ui，i=1,2,…,n

（2）初始化

按照上述编码方式随机生成N个染色体构成初始种群。

（3）约束处理

初始化产生的个体一定满足约束（13），但不一定满足约束（15）。因此需要对不满足约束条件的染色体进行可行化处理，以使其满足约束。对约束（15）按下文方式处理。

①将xi,i=1,2,…,n代入式（14）计算得wi,i=1,2,…,n。并验证是否满足约束（15），如果满足则处理下一条染色体，直到所有染色体均满足约束（15）。

②对不可行的染色体随机生成需要调整的基因位，对该基因位的数值乘调整系数α（0＜α＜1），执行操作①。利用调整系数可以控制调整的速度。

（4）交叉算子

采用双点交叉算子，随机生成两个交叉点，交换两个父体交叉点中间的部分，交换后的染色体满足约束（13），但可能不满足约束（15）。利用前文中约束处理操作对不满足约束（15）的染色体进行可行化处理。

（5）变异算子

采用双点变异算子，随机生成两个变异点，对父体中变异点中间的部分进行变异操作，按照编码方案随机生成变异点中新的基因。变异后的染色体满足约束（13），但可能不满足约束（15）。利用前文中约束处理操作对不满足约束（15）的染色体进行可行化处理

（6）选择更新操作

将父代种群，交叉，变异后得到的新个体混合后得到一个新的种群，利用选择操作在这个新种群中选择N个个体形成新的父代种群。采用轮盘赌选择方法，将适应度大的以较大的概率选为父体进行迭代。由于本模型是求极大值，则当目标函数值大于零时可直接定义适应度值为目标函数。具体操作如下：

①由于模型求极大值，因此可以用目标函数定义适应度函数。计算种群中每个个体的目标函数值，如果目标函数值大于零，定义适应值函数为目标函数，如果目标函数值为负则定义适应值为0。

④利用[0，1]上的均匀分布随机生成一个数r，若PP(k-1)＜r＜PP(k)，则选择第k个染色体

⑤重复上述操作中④N次，得到N个染色体作为父代种群。

（7）暂存机制

为了防止最优解在搜索过程中丢失，设立了暂存机制。建立了一个暂存变量用以记录在搜索过程中找到的最优解，在每次更新操作过程中计算种群中所有染色体的适应度值，并将适应度最大值与暂存变量的适应度进行比较，若该值大于暂存变量的适应度值则更新暂存变量为当前值。由于这个机制不在遗传算法内，因此该机制不影响整个遗传算法。

4 结论

由于现实交易的证券市场无法满足Markowitz投资组合理论苛刻的假设条件，因而传统的均值方差模型在实际操作中存在一定的局限性。有鉴于此，文章基于前人的研究成果进行了一些尝试性的工作。文章讨论了考虑交易成本、资金约束、最小交易批量等限制条件并引入风险偏好系数构建了风险偏好系数均值方差拓展模型。由于该模型为纯整数非线性规划，难以得到解析解。因此，针对该模型的具体形式，构建了遗传算法的具体实现过程。

[1]H.Markowitz.Portfolio Selection[J].Journal of Finance,1952,3(7).

[2]H.Soleimani,H.R.Golmakani,M.H.Salimi.Markowitz-based Portfolio Selection with Minimum Transaction Lots,Cardinality Constraints and Regarding Sector Capitalization Using Genetic Algorithm [J].Expert Systems with Applications,2009,(36).

[3]荣喜民,张奎庭,王晨亮,李践.有交易成本的证券投资研究[J].系统工程学报,2003,(5).

[4]罗秋兰,陈有禄.考虑有交易成本的证券组合的有效前沿研究[J].华中科技大学学报(自然科学版),2004,(7).

[5]R.Mansini,M.G.Speranza.Portfolio Selection with Fixed Costs and Minimum Transaction Lots[R].Report no.134,Dip.Metodi Quantitativi,University of Brescia,Italy,1997.

[6]Chang-Chun Lin,Yi-Ting Liu.Genetic Algorithms for Portfolio Selection Problems with Minimum Transaction Lots[J].European Journal of Operational Research,2008,185.

[7]余后强.Markowitz模型的改进及算法研究[D].武汉:武汉理工大学理学院,2009.

[8]H.R.Golmakani,M.Fazel.Constrained Portfolio Selection Using Particle Swarm Optimization[J].Expert Systems with Applications,2011, 38.

[9]张莉,唐万生,宋军.概率准则下组合投资的整数规划模型[J].天津大学学报(社会科学版),2003,(2).

[10]苏为华,陈颖艳.有风险偏好系数的寿险基金资产配置模型设计[J].安徽工业大学学报,2003,(5).

[11]G.J.Alexander,A.M.Baptista.Economic Implications of Using a Mean-VaR Model for Portfolio Selection:a Comparison with Mean-Variance Analysis[J].Journal of Economic Dynamics and Control,2002,26(7).