多属性群决策中综合权重调整算法研究
2013-10-20项海飞
项海飞
(温州职业技术学院,浙江 温州 325035)
0 引言
群决策是决策科学的一个重要分支,社会、科技的发展,多个科学的发展都有了相互的交叉,因此所要解决的决策问题就越来越复杂,需要集中各领域中的多个专家联合来完成决策[1]。岳超源[2]在决策理论与方法一书中指出,多属性决策是多目标决策中的一种,又称有限方案多目标决策,按照某种决策准则对具有多个属性的有限方案进行多方案选择和排序。多属性群决策是由多个决策者参与决策,在管理、经济、军事等领域有着广泛的应用,比如投资决策、项目评估、经济效益评价和人员考核等。而权重的合理性会直接影响到多属性群决策结果的准确性,因此对权重问题的研究十分重要[3]。
多属性群决策的研究主要有三个方面,即专家权重,属性权重和方案排序方法,宋光兴将权重分为主观权重和客观权重,并且给出了各自的计算方法。运用主观赋权法在方案的排序上有很大的主观随意性,如果决策者对这方面的知识或经验缺乏的话,将会影响判断。运用客观赋权法,虽然可以利用完善的数学理论来进行判定,但是忽视了主观信息,难以达到最佳的效果。因此,本文所要探讨的是将计算出属性的主、客观权重,利用各种方法把主、客观权重结合起来,从而得到综合权重。主观赋权法有专家调查法、环比评分法和层次分析法等,客观赋权法主要有熵信息法、离差最大化方法、基于方案满意度法和基于方案贴近度法。
多属性群决策问题的解决很大程度上需要属性权重的信息。方案的排序与属性的权重也密切相关,因此,需要协调好主观赋权法和客观赋权法的结果,从而选择最优。刘业政等[4]在研究调整属性和专家权重自适应时,提出用主观赋权法得到的属性和专家的权重,再用简单线性加权法来将个体决策集结成一次群决策的结果。如果得到的群决策的结果不稳定的话,则继续比较个体决策与群决策的差异,以使结果稳定。本文采用的是将主观赋权法与客观赋权法得到的结果用简单的线性加权法进行算法的调整。
1 权重调整的方法
1.1 主观赋权法的计算
设参加多属性群决策的专家群体为P={p1,p2,…pn},通过Delphi法或是AHP法等主观赋权法来求得专家pn的权重为uk
其中,0≤uk≤1,k=1,2,…, 且∑uk=1
假设多属性群决策的备选方案为M={m1,m2,…,mn},则设评价属性集为A={a1,a2,…,an},属性am的权重为tj
其中,0≤tj≤1,j=1,2,…, 且∑tj=1
设专家pn对备选方案pn评定后,得到的得分矩阵,设为Ck=()n*m,k=1,2,… i=1,2,…j=1,2,…
利用加权和公式,由初始得到的专家权重和属性权重,来计算出单个专家的各方案得分为:

利用单个专家的各方案得分可以计算出专家群决策结果的各方案得分
Xi=∑ykiuk
因此,专家对各方案的评估结果矩阵为B=[bik]n*m其中bik=Ykii=1,2,…,k=1,2,…
这种方法虽然比较简单,但是没有达到使各专家意见与群体意见一致的目的。因此对专家的个体决策结果与专家群体决策结果进行偏离权重的计算。
设个体决策结果与群体决策结果的偏差为
Fk=(fk1,fk2,…,fkn)T其中fki=Yki-Xik=1,2,… i=1,2…因此,我们可以得到专家个体决策结果与群体决策结果的总偏差量为

通常来说群体的决策结果代表了专家的共同意愿,决策结果应趋于一致的。即fki最理想的情况下应该是零向量,所以专家的偏离权重为

其中 ,k=1,2,…
如果单个专家的偏差越大,与群体的共同意愿偏离越远,则对应所赋予的偏离权重就越小,不过不能只为了寻求意见上的一致而忽略了部分决策者对结果的影响,因此还要从专家个体提供的信息量方面继续调整专家的权值。除此之外,个体决策与群体决策的偏离结果还可以用下面这种方法表示

1.2 客观赋权法的计算
熵理论是作为物质系统状态的一个函数,表征系统的紊乱程度,并且是无序状态系统的量度。根据信息熵的定义和原理,当系统处于不同的状态,并设每种状态出现的概率为pi(i=1,2,…n)
因此,整个系统的熵则为

当pi=0,时,pilog2pi也为0,当系统各种状态的概率为等概率时,即pi=Vn,此时就有最大熵值。
也就是,E(p1,p2,…pn)≤E(1/n,1/n,…1/n)=log(n)
熵可以用来计算不同属性所代表的信息量的多少。当每个属性值在不同方案上的水平值越会越接近的,从而其整个熵值就会越大。
根据前面专家的个体评估结果矩阵B=[bik]n*m,我们就可以计算出第k个专家的熵值
Ek=-∑miklog2mik,m=1,2,…
其中mik=bik/∑bik
并且当mik=0时,miklog2mik=0
根据前面,我们可以知道,当mik值相等时,第k个专家的熵值也达到最大值,因此,最大熵值为(Ek)max=log2n,对熵值归一化处理,可以得到

根据熵值来求得互补值,经过归一化处理后可以作为熵权。
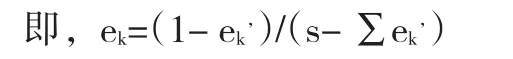
其中,0≤ek≤1 ,k=1,2,… ∑ek=1
万俊等[5]在研究基于熵理论的多属性群决策专家权重的调整算法时提出,当某一决策者的决策结果与群体决策结果差异越小,则对于方案排序起的作用的有用信息量就会越小,反之,则会越大。
1.3 综合权重的调整
在得到主观赋权法的偏离权值和客观赋权法的熵权值之后,我们利用简单的线性加权法,来进行权重算法的调整,调整为

其中,k=1,2…t,g值可以根据自己的情况来赋值。
如果不考虑熵权的数值,只看重偏离权重的结果,来要求个体决策结果与群体决策结果的偏差尽量小,那么该调整的算法必定收敛。然而,实际中并没有调整决策者的结果,只是相应的调整了各个决策者的权重值,因此求出来的专家熵权数值是不会发生改变的。这时我们将熵权数值和偏离权数值用线性关系综合起来,进行对专家的权重进行调整,得到的算法是收敛的。
2 实例分析
某公司要对即将上市的几种商品能否常驻市场进行开发研究,选择3个专家对4种商品的5个方面的指标进行打分评价,分别为商品质量(n1)、商品的包装(n2)、商品的研发能力(n3)、商品的创新力(n4)和商品的价格(n5)。
专家的打分情况如下表1所示,其中p表示专家,m表示方案,专家对属性的打分数值为

表1 专家打分表
将表1中的专家打分,进行简化下,得到如下表2
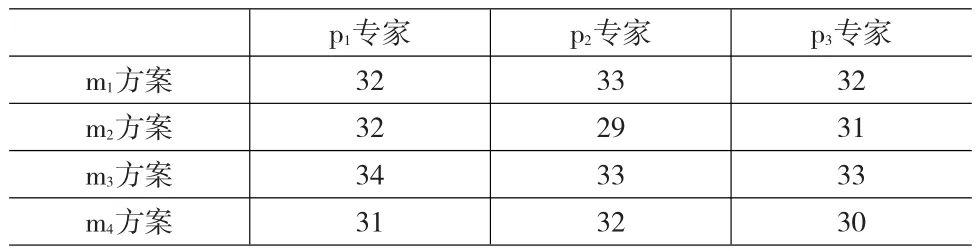
表2 初始简化计算结果
因为专家个体在决策结果上有所分歧,因此,需要使用到上面所讲到的权重调整算法。结合各个专家给定的评定结果来调整权重。根据算法编制程序,并输入数据,经过 次的迭代调整后,结果趋于稳定,可以得到最终专家的综合权重和备选方案的得分。
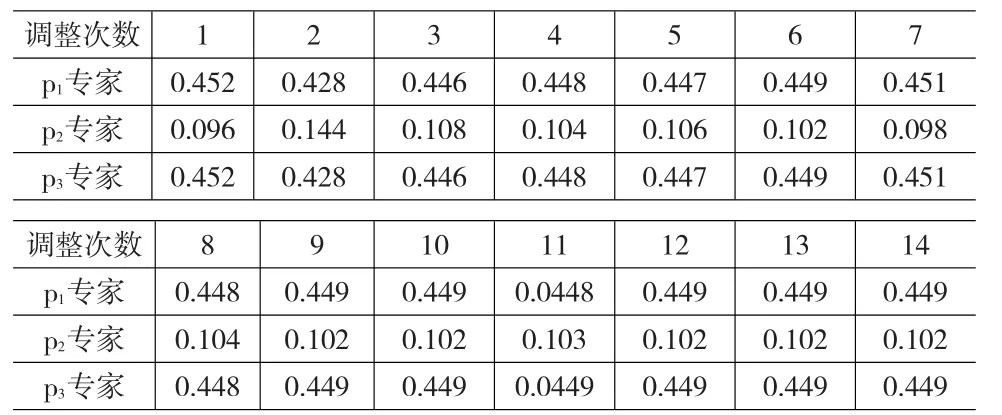
表3 m1方案偏离权重的变化表
3 结论

表4 m2方案偏离权重变化表
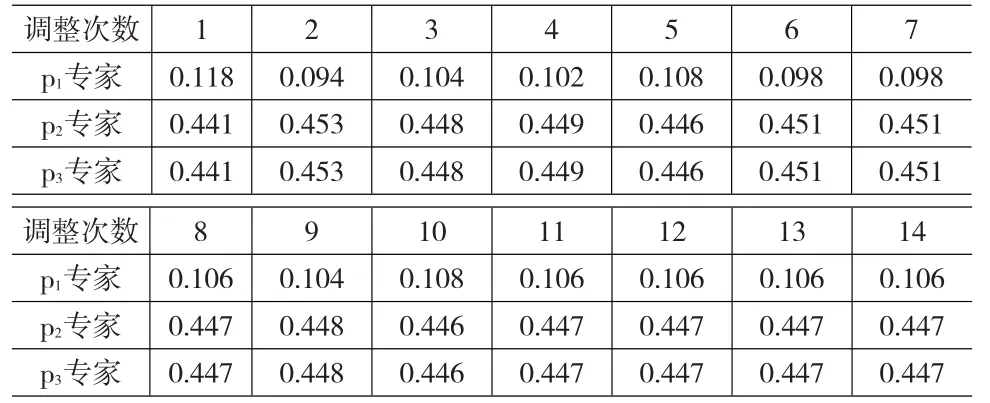
表5 m3方案偏离权重变化表
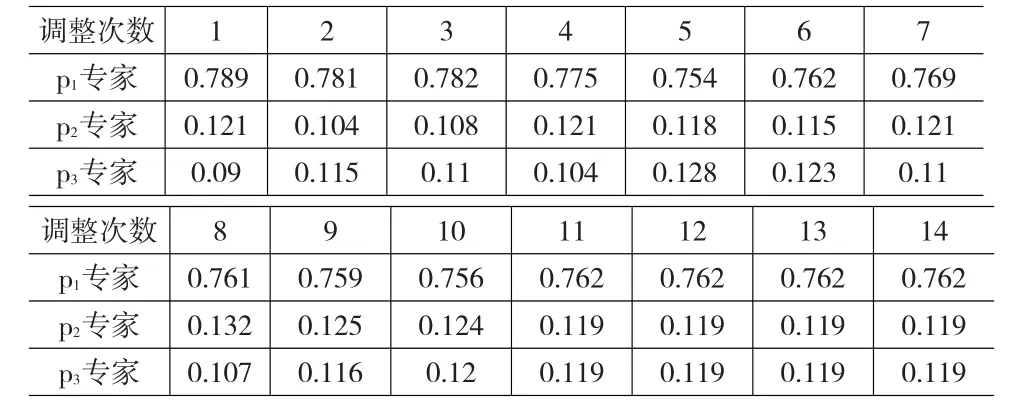
表6 m4方案偏离权重变化表
本文所研究的是在主观权重已知的基础上,利用偏离度和熵权的方法来计算客观权重的数值,从而对个体决策的权重进行调整。通过调整后得到的综合权重的数值更加准确的反映了真实情况,较为合理。并且通过具体的事例验证了这种方法的可行性。
[1]徐改丽,吕跃进.一种基于灰色关联度的多属性群决策方法[J].计算机工程与应用,2012,48(9).
[2]岳超源.决策理论与方法[M].北京:科学出版社,2003.
[3]刘培德,张新.一种基于区间灰色语言变量几何加权集成算子的多属性群决策方法[J].控制与决策,2011,26(5).
[4]刘业政,徐德鹏,姜元春.多属性群决策中权重自适应调整的方法[J].系统工程与电子技术,2007,29(1).
[5]万俊,邢焕革,张晓辉.基于熵理论的多属性群决策专家权重的调整算法[J].控制与决策,2010,25(6).
[6]周延年,朱怡安.基于灰色系统理论的多属性群决策专家权重的调整算法[J].控制与决策,2012,27(7).
[7]徐泽水,达庆利.多属性决策的组合赋权方法研究[J].中国管理科学,2002,10(2).
[8]苑娟,万焱,褚意新.熵理论及其应用[J].中国西部科技,2011,10(5).
