快速路交通事件检测方法

李红伟 陆 键 姜桂艳 马永锋

(1 东南大学交通学院，南京210096)

(2 上海交通大学船舶海洋与建筑工程学院，上海200240)

(3 吉林大学交通学院，长春130022)

作为城市路网系统中的主要道路，快速路在整个城市交通系统中发挥着重要作用，如上海快速路道路面积占市中心道路面积的5%，却承担了市中心20%的交通量［1］.因交通事件引起的拥堵已占上海快速路总拥堵的50%～75%［2］.准确、及时的交通事件自动检测(automatic incident detection，AID)算法可减少因交通事故造成的拥堵时间，降低人员伤亡以及财产损失.

目前，流行的交通数据采集设备是环形线圈检测器和视频检测器.与视频检测器相比，环形线圈检测器因具有价格适中，在雨、雾等恶劣天气下仍可正常工作等优势，而被广泛应用.以线圈数据为基础的AID 算法包括模式识别、统计预测、时间序列、交通流理论、智能检测5 类，代表算法分别为California 算法［3］、贝叶斯算法［4］、自回归综合移动平均算法［5］、小波算法［6］以及神经网络算法［7］.这些算法均存在缺陷:California 算法误警率高;贝叶斯算法复杂;自回归综合移动平均算法复杂，误警率高;小波算法检测率低;神经网络算法复杂［8-9］.此外，以上算法对低流量状态下的事件检测效果极差.

本文提出一种既能保证较高检测率(detection rate)和较低误报率(false alarm rate)，又适用于各种流量的快速路AID 算法.

1 数据来源

本文提取了某城市快速路高架上的交通流历史数据进行研究.该路段全长约14 km，包括主线、8 个出入口匝道和3 个立交，全程无信号控制.

由于快速路主线、匝道与高架上的交通流冲突类型、车辆运行特征存在差异［10］，匝道分流点、合流点以及减速连接部、加速连接部处布设检测器［11］.主线处，平均每500 m 左右设置一个检测截面，共布设88 组检测器.匝道进口和出口附近各设置一个检测截面，共布设42 组检测器.路段两端立交匝道出入口各设置一个检测截面;第3 个立交出入口匝道上布设间距约200 m 的2 个检测截面，立交共布设30 个检测器.已有研究认为，事件检测中检测器间距在200～500 m 之间是合适的，由此可知，本文中检测器布设间距合理［12］.

检测器可采集流量、地点平均车速(简称速度)和时间占有率(简称占有率)等参数，采集间隔为5 min.采集时间为2008-04-24—2008-05-26 每周的第1 个工作日.数据采集期间天气晴好，路段沿线无大型活动和特殊交通管制，共采集了191 起交通事件，东侧主线、东侧匝道、西侧主线、西侧匝道各75，31，56，29 起.东侧数据用于交通事故数据特征分析和建模，西侧数据用于验证模型的有效性.

2 理论基础

2.1 时间序列

交通事故的时间序列包含事故发生、发展趋势，可用于设计AID 算法［13］.图1给出了交通量数据时间序列.其中，x 轴为横向时间序列，指数据以24 h 为坐标轴进行排列的序列;y 轴为纵向时间序列，指数据以相同工作日(如周一)为坐标轴进行排列的序列;z 轴为流量(辆/min).

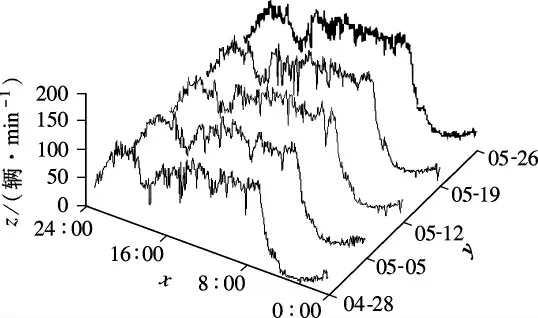
图1 交通量数据时间序列

现有的AID 算法多以横向时间序列上的数据为研究基础，对数据的稳定性和正态拟合性要求较高.本文利用均值标准误差(standard error of mean，SEM)和Kolmogorov-Smirnov 正态性检验对比分析2 种时间序列上数据的波动性和正态拟合性，以选择更适合建模需求的时间序列.

图1中，横向时间序列交通流变化趋势复杂，为降低其波动性，根据其变化趋势，将横向时间分为4 段:①低峰，00:00—04:30;②激增，04:35—07:30;③高峰，07:35—17:30;④缓降，17:35—00:00.各阶段的SEM 值和Kolmogorov-Smirnov验证结果(P)如表1所示，其中，SEM 值越大，说明数据波动性越大;P 为显著性水平，若P ＞0.05，表示没有足够证据证明样本不符合正态分布，反之，表示数据不符合正态分布.

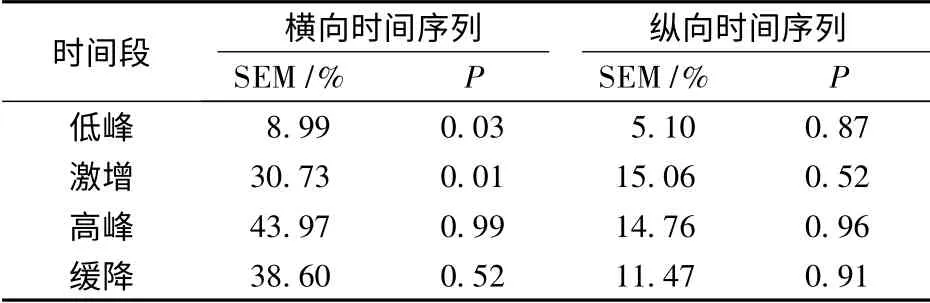
表1 SEM 值与Kolmogorov-Smirnov 检验

表1中，横向时间序列上数据的SEM 值约为纵向时间序列的2～3 倍，说明纵向时间序列更稳定;纵向时间序列上数据的P 值均大于0.05，说明纵向时间序列正态拟合性更好.因此，本文选择数据波动性更小、正态拟合性更显著的纵向时间序列上的数据为建模基础，建立快速路AID 算法.

2.2 突变理论

突变理论研究从一种稳定组态跃迁到另一种稳定组态的现象和规律，能较好地解释和预测自然界和社会上的突然现象［14］.交通事件下的交通流变化趋势符合突变现象.未发生事件时，交通流参数在一定范围内小幅上下波动;事件发生前期，交通流参数急剧降低;事件持续期间，交通流参数基本稳定在一定范围内;事件发生后期，交通流参数急剧增加;事件结束，交通流参数在一定范围内小幅波动.交通参数的突变特征可归纳为:

①多模态.事件未发生和发生时，交通流参数在不同区间内上下波动.

②不可达.未发生事件时，交通流参数所在区间是事件过程中的参数不能达到范围，反之亦然.

③突跳.事件发生时，交通流参数由一个稳定的数值范围突然跳到另一个稳定的数值范围，这种变化是不连续的.

3 模型建立

3.1 参数选取

参数的选择关系到AID 算法的效果.已有的AID 算法多采用占有率或流量作为输入参数.事件发生时，单位车辆通过检测器的时间增加，导致占有率增大;交通拥堵时，占有率亦可能增大.单纯从占有率判断是否发生交通事件不尽合理，流量存在同样的问题.这表明，依靠单个交通参数无法很好地体现交通流运行状态.事件发生过程中，占有率数值明显增大，流量、速度明显降低.因此，本文利用环形线圈检测到的事件状态下的流量、速度和占有率3 个参数设计新的AID 算法.

3.2 交通事件影响指数

根据统计理论和突变理论，提出交通事件影响指数I.I 定义为交通流参数预测值与实测值之比，计算公式如下:

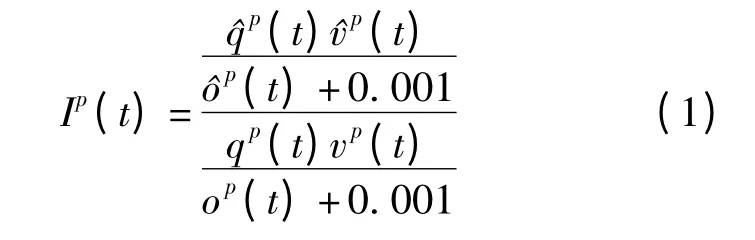
式中，Ip(t)为t 时刻p 地点的交通事件影响指数;qp(t)为t 时刻p 地点的实测流量;vp(t)为t 时刻p地点的实测速度;op(t)为t 时刻p 地点的实测占有率;^qp(t)为正常交通状态下t 时刻p 地点的预测流量;^vp(t)为正常交通状态下t 时刻p 地点的预测速度;^op(t)为正常交通状态下t 时刻p 地点的预测占有率.

事件发生后车流可能静止，为防止检测器检测到的占有率为0，占有率加上一个常数0.001.

由于纵向时间序列稳定性好，从预测的简易性考虑，用移动平均法预测交通参数，即

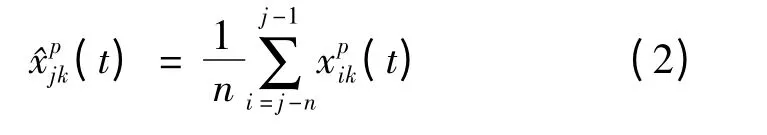
预测精度取决于时间窗口尺度n.若n ＜3，预测数据精度小于90%;若n ＞8，即2 个月后，预测数据精度降低，这是由于交通流具有季节性.因此，n∈(3，8).

3.3 交通事件影响指数特征分析

预测值由正常交通状态下的历史数据计算得到.未发生事件时，预测值与实测值相差不大，I 在数值1 左右波动;事件发生时，分母中的qp(t)和vp(t)降低，op(t)增大，实测值显著降低，预测值明显大于实测值，I 值远远大于1.事件状态下的I 值变化特征如图2所示.

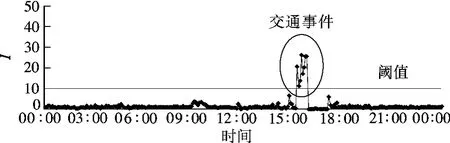
图2 事件状态下的事故影响指数变化趋势

3.4 确定阈值

本文利用I 值累积分布曲线(见图3)及检测率(RD)和误报率(RFA)关系曲线(见图4)确定交通事件判断的阈值.图3中，RD值等于100%减去该阈值下的累积百分数.I =8 时，RD=100%;I=9 时，RD=95%;I=10 时，RD=90%;I =11 时，RD=85%.图4中，I =8 时，RFA=36.72%;I =9时，RFA=27.18%;I =10 时，RFA=1.69%;I =11时，RFA降至0%.由以上结果分析得出，阈值应取10.

基于以上原因，“是否发生交通事件”的问题就归结为“在t 时刻的I 值是否属于某个区间”的下述检验问题:

原假设H I∈(0，10)

对立假设K I∉［10，+∞)

假设成立，未发生事件;反之，发生事件.

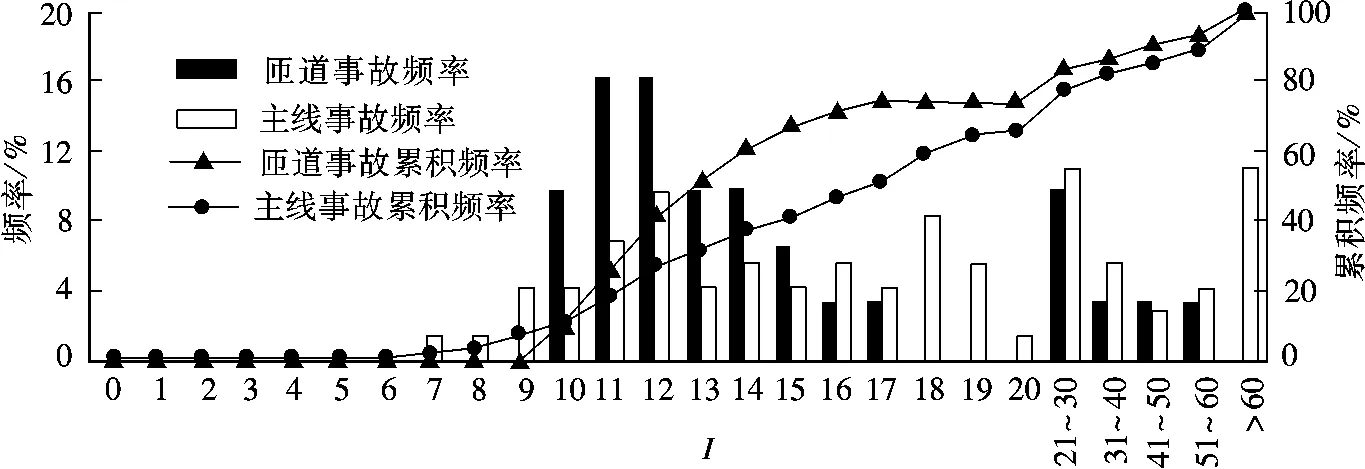
图3 事故影响指数的频率及累积频率

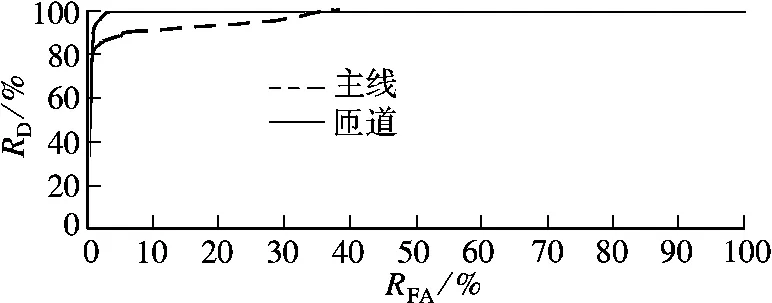
图4 RD-RFA曲线

4 模型验证

4.1 对比检验

一般用检测率RD、误报率RFA和平均检测时间DMTT三个指标检测AID 算法的性能.作为经典的AID 算法，California 算法应用效果已在实际应用中得到充分证明，本文利用California 算法验证本文提出的事件数据影响指数算法的性能，对比结果见表2.

表2 检测结果对比 %

由表2可以得出以下结论:

1)California 算法RD=85%，事件数据影响指数算法RD=94.56%，后者的RD值比前者高近10%，说明本文算法的检测率可以满足检测率要求.

2)California 算法RFA=0.64%，事件数据影响指数算法RFA=0%，后者的误报率低于前者，说明本文算法基本不会误判交通事件.

3)若以California 算法检测出事件的时间为参考时间，本文算法可提前5 min 检测出交通事件.

权衡RD，RFA及DMTT三个评价指标，可以发现本文算法的检测效果更好.

4.2 不同阈值检测效果对比

西侧主线、西侧匝道的交通事故数分别为56，29.当阈值为12，11，10，9，8 时，西侧主线检测出的交通事故数分别为38，42，54，55，56，被误判的交通事故数为0，0，0，1，7;西侧匝道检测出的事故数为22，25，28，29，29，被误判的交通事故数为0，0，0，2，5.

不同阈值下的RD和RFA值如表3所示.对西侧主线而言，RD= 100% 时，阈值为8，RFA=12.50%;阈值为10，11，12 时，RFA均为0%，RD值分别为94.64%，75.00%和67.86%.

表3 不同阈值下的检测结果 %

为了保证误检率和检测率均达到最优，选择I=10 作为阈值.同理，西侧匝道的交通事件检测方法的最优阈值同样为10.此结果说明了本文提出的阈值确定方法是正确的.

4.3 不同流量情况下的检测效果

图5中，事件1，2，3，4 的发生时段分别为0:55—1:15，5:55—6:05，15:15—15:50，20:20—20:55，其中，事件1，2，3 为一次事故，事件4 为二次事故.结合图1中交通流量的4 个时段，事件1发生在低峰时段，事件2 发生在流量激增时段，事件3 发生在高峰时段，事件4 发生在流量缓降时段.

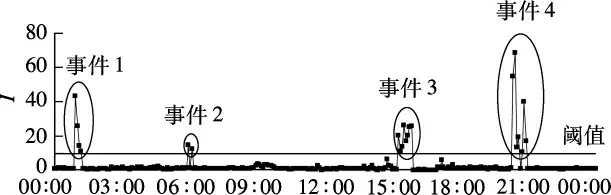
图5 不同流量下的事故影响指数变化趋势

由图5可得到以下结论:

1)大于阈值的I 值所在时间内均发生交通事件;小于阈值的I 值所在时间内均未发生交通事件.

2)事件发生过程中，当I 值变化曲线为U 形曲线时，表示本次事件发生了二次事故，如事件4所示.

3)I 值对低流量比高流量更敏感，说明本方法不仅能在高峰、平峰时段检测出交通事件，对低流量时发生的交通事件检测效果更好，即本文算法适用于各种流量.

4)未发生事件时，I 值在1 左右上下浮动，浮动范围不超过10;发生事件时，I 值突变，突变幅度很大，说明本文算法的检测性能不受交通流变化趋势的影响，只受交通事件的影响.这也解释了本文算法比California 算法检测性能更好的原因，同时说明了本文算法的阈值更容易确定.

5 结论

1)本文算法的检测率比California 算法高出近10%，误检率为0，可提前5 min 检测出交通事件.说明本文算法具有良好的性能.

2)I 值在低流量时比高流量反应更敏感，说明本算法不仅能在高峰、平峰时段检测出交通事件，对低流量时发生的交通事件检测效果更好，即本文算法适用于各种流量的情况.

3)本文算法的检测性能不受交通流变化趋势的影响，只受交通事件的影响.

References)

［1］唐海雯.实时监控 及时处置 为排堵保畅做贡献［J］.交通与运输，2006(2):10-11.

［2］姬杨蓓蓓，张小宁，孙立军.基于贝叶斯决策树的交通事件持续时间预测［J］.同济大学学报:自然科学版，2008，36(3):319-324.

Jiyang Beibei，Zhang Xiaoning，Sun Lijun.Incident duration prediction grounded on Bayesian decision method based tree algorithm［J］.Journal of Tongji University:Natural Science，2008，36(3):319-324.(in Chinese)

［3］Payne H J，Helfenbein E D，Knobel H C.Development and testing of incident detection algorithms［R］.Washington，DC，USA:Federal Highway Administration，1976.

［4］Abuelela M，Olariu S.Automatic incident detection in VANETs:a Bayesian approach［C］//IEEE Vehicular Technology Conference.Barcelona，Spain，2009:1-5.

［5］Moynihan G P，Fonseca D J，Brumback T，et al.Design of a decision support system for road incident detection and characterization［C］//Proceedings of the 2009 ASCE International Workshop on Computing in Civil Engineering.Austin，USA，2009:613-322.

［6］Jeong Y-S，Castro-Neto M，Jeong M K，et al.A wavelet-based freeway incident detection algorithm with adapting threshold parameters［J］.Transportation Research Part C，2009，19(1):1-19.

［7］Ritchie S G，Cheu R L.Simulation of freeway incident detection using artificial neural networks［J］.Transportation Research Part C，1993，1(3):203-217.

［8］Jian L，Shuyan C，Wei W.A hybrid model of partial least squares and neural network for traffic incident detection［J］.Expert Systems with Applications，2012，39(5):4775-4784.

［9］Subramaniam S.Literature review of incident detection algorithms to initiative diversion strategies［R］.Blacksburg，VA，USA:Virginia Polytechnic Institute，1991.

［10］王欣，李文权，王炜.基于驾驶行为共性的回波速度解释及仿真［J］.东南大学学报:自然科学版，2007，37(4):691-694.

Wang Xin，Li Wenquan，Wang Wei.Interpreting and emulating echo wave speed based on common characteristics of driving behavior［J］.Journal of Southeast University:Natural Science Edition，2007，37(4):691-694.(in Chinese)

［11］陈雨人，郑仕文，童世鑫，等.区域高速公路网络交通事件传感器布设方法研究［J］.公路交通科技，2010，27(11):143-148.

Chen Yuren，Zheng Shiwen，Tong Shixin，et al.Study on deployment of traffic incident detectors for regional expressway network［J］.Journal of Highway and Transportation Research and Development，2010，27(11):143-148.(in Chinese)

［12］Awadallah F.Incident detection:selection of appropriate technologies and methodologies［J］.Road Transport Research，2002，11(2):50-56.

［13］Daniel D G，Francisco J，David G O.Wavelet-based denoising for traffic volume time series forecasting with self-organizing neural networks ［J］.Computer-Aided Civil and Infrastructure Engineering，2010，25(7):530-545.

［14］Stamovlasis D，Tsaparlis G.Applying catastrophe theory to an information-processing model of problem solving in science education ［J］.Science Education，2010，96(3):392-410.