LTE系统中基于估计波束到达角的多用户调度算法

彭张节 洪 赟 许 威 赵春明

(1 东南大学移动通信国家重点实验室，南京210096)

(2 联发通讯科技(苏州)有限公司，苏州215021)

在移动通信系统中，MIMO 信道建模是一个关键问题.3GPP TR 25.996［1］中提出了基于子径的空间信道模型(SCM)，这种建模方式既控制了复杂度，又能够很好地模拟真实环境，因此在MIMO系统研究中被广泛应用.在LTE 系统以及未来LTE－A 系统中，重点考察基于SCM 信道模型的通信系统性能.为了进一步提高通信系统的性能，多用户MIMO［2－3］成为研究的重点，其性能增益很大程度上取决于多个参与空分复用的用户间的信道相关性.在SCM 信道模型中，用户间的信道相关性取决于基站与移动台相邻天线间的距离、波束到达角等诸多因素［4－5］.波束到达角的估计算法很多，如MUSIC 类算法［6］、ESPRIT 算法［7］等，这些经典估计算法都需要求解特征向量，复杂度较高.

理论和实践表明，采用合适的用户调度算法能够明显提高系统性能.当前，用户调度技术主要需要解决公平性［8］和计算量2 个问题.其中，公平性问题可以通过加入调度因子来实现，最典型的算法是比例公平算法(PFS)［9］;而运算复杂度高的问题始终是一个局限，很多用户调度算法的复杂度高且反馈量大，对信道瞬时变化也非常敏感.

针对上述问题，本文提出了一种复杂度较低的波束到达角估计算法.此外，本文还提出了一种基于波束到达角的调度算法，该算法对于信道的短时时变具有鲁棒性，且计算复杂度也相对较低.

1 SCM 信道模型及用户相关性

根据文献［1］中的SCM 信道模型，对于基站(BS)配置S 根天线、移动台配置U 根天线的系统，在3GPP TR 25.996 中，一条可辨径的冲击响应可表示为

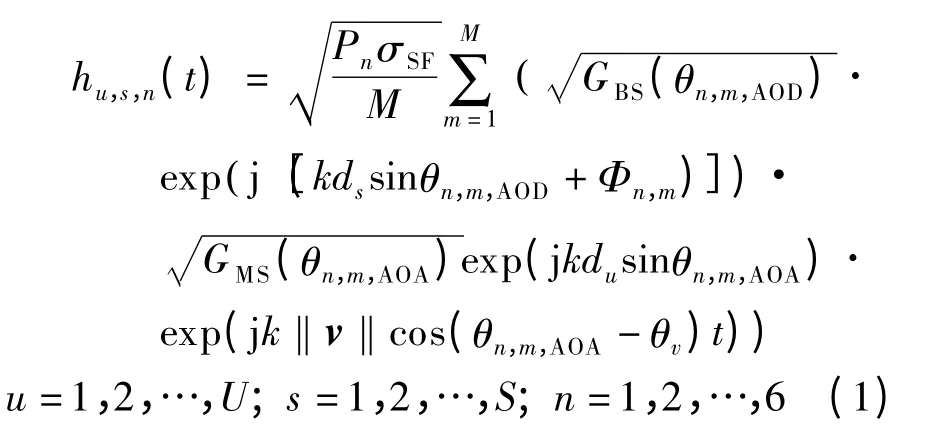
式中，hu，s，n(t)为用户第u 根天线与基站第s 根天线之间的第n 条可分辨径的时域冲击响应;M 为子径数，3GPP TR 25.996 中M =20;Pn表示第n条径的功率;σSF为阴影衰落参数;θn，m，AOA，θn，m，AOD分别为第n 条径中第m 条子径的到达角度和离开角度;为基站侧天线在方位角θn，m，AOD方向上的增益;为移动台侧天线在方位角θn，m，AOA方向上的增益;k =2π/λ，λ为波长;ds为基站侧第s 根天线的位置;du为移动台侧第u 根天线的位置;Φn，m为第n 条径中第m 条子径的初始相位;v 为移动台(MS)的速度矢量;θv为移动台速度方向与移动台天线阵列方向的夹角.本文算法的主要思想是根据上行波束到达角来进行用户调度.

用户调度的核心思想可以表述为:挑选信道相关性较小的用户组成空分复用，以增加信道容量，提高系统性能.因此，基于式(1)中2 个用户间的相关性就显得相当重要.针对式(1)所表达的一般情况进行分析较为困难.为了简化分析，本文首先进行一些合理的假设.虽然分析过程做了一定假设，但最后的仿真结果表明，本文算法对于式(1)所描述的一般情况也适用，能够取得良好的效果.本文假设如下:①天线为全向天线，在各个方位角上增益相等，设增益为1;②无线信道有明显的方向性，不妨首先假设为单径;③不考虑角度扩散，即属于同一可分辨径的子径具有相同的到达角;④基站侧天线数为S，相邻天线间距为半波长，移动台配置单根天线.则式(1)可简化为

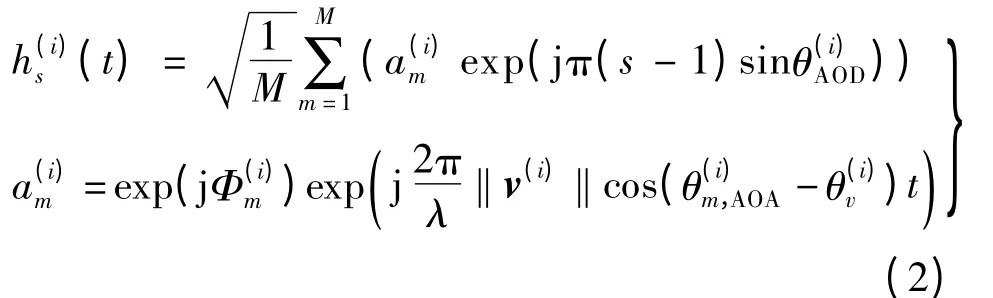
式中，

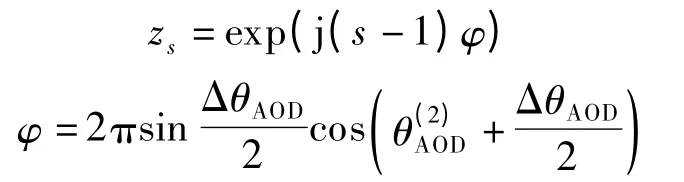
显然，z1，z2，…，zS是幅度为1 的复数，其相角成倍数关系，即为0，φ，…，(S－1)φ，如图1所示.

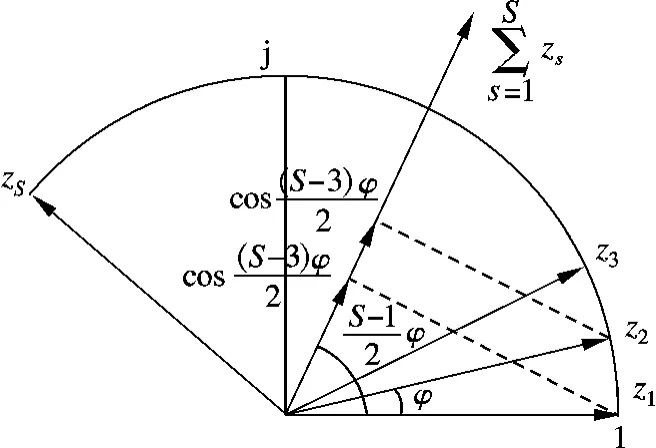
图1 式(4)的推导附图

一般来说，基站侧天线数S 为偶数，故f(ΔθAOD)的最终相位为(S－1)φ/2.利用图1，可计算出其幅度，则信道的相关性可表示为

式中，θ(2)AOD表示用户2 的波束到达角.因考察的是统计意义上的相关性，故将θ(2)AOD作为积分变量，通过计算式(5)对于θ(2)AOD的期望，反映出此模型的统计相关性.由单一用户波束到达角的随机性，可假设θ(2)AOD的分布为均匀分布U(0，2π)，对式(5)求期望可得

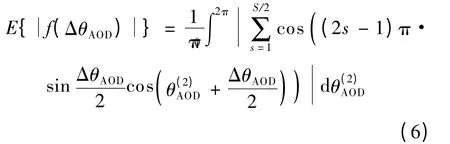
图2给出了基站天线数S =2，4，8 时式(6)的积分数值解，基站侧相邻天线间距离为半波长.由图可知，对于同一根曲线，从总体趋势上来看，相关性是ΔθAOD的递减函数，曲线波动是模型简化造成的.波束到达角相差较大，说明2 个用户信道环境在地理位置上相距较远，经过的空间散射路径也就相对独立.对于不同曲线而言，增加基站数能够降低相关性，这是由于多天线能够提供相对较高的自由度，使得不同用户信道之间变得更加独立.

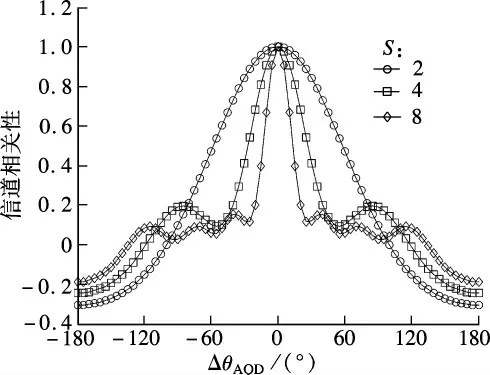
图2 式(6)的数值积分值

2 波束到达角估计算法

由第1 节的分析可以看出，信道的相关性与ΔθAOD直接相关.故基站需利用波束到达角估计技术来估计出波束到达角.

由文献［1］可知θn，m，AOD= θBS+ δn，AOD+Δn，m，AOD，其中，θBS为BS 天线方向与视距方向的夹角，δn，AOD为第n 条可分辨径中离开方向与视距方向的夹角，Δn，m，AOD为第n 条可分辨径中第m 条子径的离开方向的偏离角度.同时由文献［1］可知，Δn，m，AOD较小(特别在宏小区环境中)，故可认为同条可分辨径中每条子径的sinθn，m，AOD相等，为其均值假定基站与用户侧相邻天线间距离分别为dsλ，duλ，则ds=(s－1)dsλ，du=(u－1)duλ，故式(1)可简化为

式中，

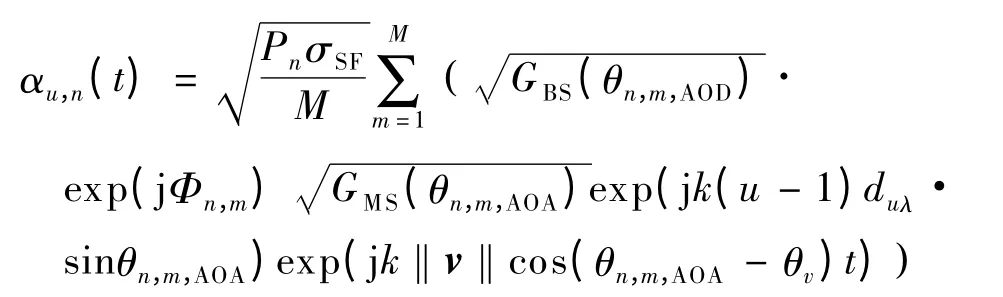
系统中每个用户的时域冲击响应都由6 条可分辨径叠加而成.为了方便分析，本文仅分析最强径的时域冲击响应其中系统中用户的信道矩阵为H = [h1，h2，…，hU]H，其中为第u 个1 ×S 的信道向量，为入射信号的方向向量，其维度为1 ×S.则信道矩阵H 可以表示为

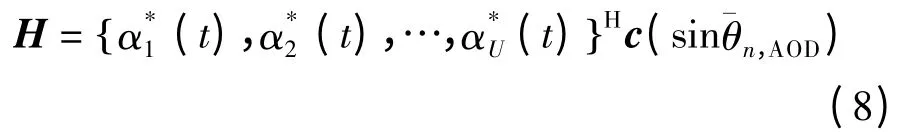
由式(8)可知，该信道矩阵的表达式与经典的DOA 估计算法的天线阵元信道矩阵相类似，可以采用经典算法进行估计，但经典算法需求解特征向量，复杂度较高.针对上行信道信息已知的情况，本文提出了一种低复杂度DOA 估计算法.在式(8)中，只有向量包含信号DOA 的方向信息，若对信道矩阵H 右乘与信号DOA 方向一致的向量则可得到最大值，即应满足

故SCM 信道的空间谱函数为

在信道矩阵只有1 个离开角度时，利用式(10)得到的空间谱函数曲线如图3所示.图中，基站配置4 根发送天线，用户配置1 根接收天线，基站侧相邻天线间距离为半波长，信号波束到达角为0.759 0°.另外，为了使纵坐标统一，将谱函数的幅度进行归一化.谱函数曲线只有1 个波峰，峰值所在角度为0.759 0°，故利用式(9)可以精确估计出波束到达角.

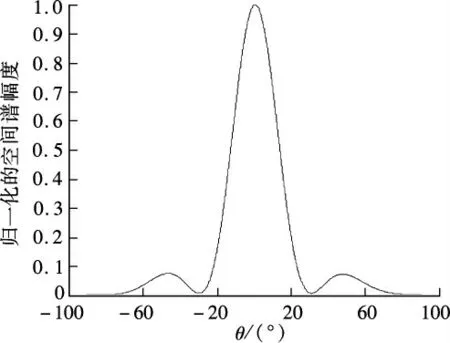
图3 SCM 信道空间谱函数

3 基于波束到达角的用户调度算法

根据第1 节的分析可知，如果用户到达角间相差较大，则相关性较小.而在第2 节中，对波束到达角进行估计后，获得，当用户间相差较大时，用户间的波束到达角也相差较大，故本文用来度量波束到达角的隔离度.由此设计出一种基于波束到达角的用户调度算法，具体步骤如下:

①系统初始化.检测到活跃用户数I，并任意选择L 个用户，形成空分复用.

②判断当前时刻是否进行用户调度，若I≤L，则无需调度，系统为当前I 个用户传输数据;否则，转入步骤③.

⑤对于每个子集Zl(l=1，2，…，L)，计算其中所有用户信道矩阵的Frobenius 范数.

⑥在每个子集中选择具有最大Frobenius 范数的用户，即为最终的调度用户集合，系统将为其传输数据.

⑦下一个传输时刻到来，返回步骤②.

此算法的优点在于:①复杂度明显减少，更适合于实际系统;②此算法根据估计的波束到达角进行调度，具有较高的实际应用价值;③由于到达角信息变化缓慢，可以相隔较长时间估计波束到达角，进一步减小调度时的运算量;④调度方案设计完全基于实际的无线信道环境，更能模拟真实情况.

4 仿真结果

仿真基于TD－LTE 系统，无线信道采用3GPP TR 25.996 中所叙述的SCM 模型，波达方向设为主径的方向.具体仿真参数见表1.

表1 TD-LTE 系统仿真参数

当I=10，L =2 时，随机调度、基于容量的用户调度和基于波束到达角的用户调度这3 种算法的系统误帧率见图4.其中，随机调度算法是指在每个调度时刻来临时，任意选取10 个用户中的2 个，为其传输数据;这种算法复杂度低，并能保证一定的公平性，但由于没有利用信道信息，故并未得到多用户增益，也是误帧率最高的一种算法.基于容量的调度是指在每个调度时刻来临时，通过遍历所有CLI种用户组合，选择使得信道容量最大的那一个用户集，为其传输数据;这种算法性能最好，但由于它是一种遍历性算法，复杂度高.本文提出的基于波束到达角的调度算法性能略差于基于容量的调度算法，但是相比于随机调度算法，能够获得明显的多用户增益;同时，该算法的运算复杂度O(I)较低，且反馈量少，更适合在实际系统中实现.

图4 3 种调度算法的系统误帧率曲线

公平性问题是衡量调度算法性能优劣的一个重要指标.图5为I=10 时基于估计波束到达角调度算法的公平性柱状图.由图可知，该算法并未导致明显的公平性问题.其原因在于，算法步骤中，根据Frobenius 范数选择用户时，信道范数的较快时变使得该集合内的所有用户都有被服务到的机会.因此，从公平性角度来说，本文算法也是一种较为可行的方案.

图5 基于波束到达角调度算法的公平性柱状图(I=10)

5 结语

本文研究了SCM 信道模型特点，由3GPP TR 25.996 中的SCM 信道模型公式出发，推导得到相关性与波束到达角之差的函数关系，估计出波束到达角，进而提出了一种基于估计波束到达角的用户调度算法.该用户调度算法通过牺牲较小的系统性能以降低反馈量和系统复杂度，并且对于用户信道的瞬时变化具有较好的鲁棒性.仿真结果表明，这种用户调度算法不但能够获得良好的多用户增益，还能显著降低算法复杂度.

References)

［1］3GPP.Spatial channel model for multiple input multiple output simulations(3GPP TR 25.996，v8.0.0)［EB/OL］.(2009－01)［2012－04－15］.http://www.etsi.org/deliver/etsi_tr/125900_125999/125996/08.00.00_60/tr_125996v080000p.pdf.

［2］Gesbert D，Kountouris M，Heath J R W，et al.From single user to multiuser communications:shifting the MIMO paradigm［J］.IEEE Signal Processing Magazine，2007，24(5):36－46.

［3］Jankiraman M.Space-time codes and MIMO systems［M］.Massachusetts，Norwood，USA:Artech House，2004.

［4］Wang J，Zhao J，Gao X.Performance simulation and analysis of polarized MIMO systems［C］//Proceedings of the 2008 International Conference on Microwave and Millimeter Wave Technology.Nanjing，China，2008:2014－2017.

［5］Wang J，Zhao J，Gao X.Modeling and analysis of polarized MIMO channels in 3D propagation environment［C］//Proceedings of the 21st Annual IEEE International Symposium on Personal，Indoor and Mobile Radio Communications.Istanbul，Turkey，2010:319－323.

［6］Schmidt R O.Multiple emitter location and signal parameter estimation［J］.IEEE Transactions on Antennas and Propagation，1986，34(3):276－280.

［7］Roy R，Kailath T.ESPRIT—estimation of signal parameters via rotational invariance techniques［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1989，37(7):984－995.

［8］Nandagopal T，Lu S，Bharaghavan V A.Unified architecture for the design and evaluation of wireless fair queuing algorithms ［J］.Wireless Networks，2002，8(2):231－247.

［9］Li L，Pal M，Yang Y R.Proportional fairness in multirate wireless LANs ［C］//Proceedings of 27th IEEE Conference on Computer Communications.Phoenix，AZ，USA，2008:1004－1012.

［10］Sadek M，Tarighat A，Sayed A H.A leakage－based precoding scheme for downlink multi－user MIMO channels［J］.IEEE Transactions on Wireless Communications，2007，6(5):1711－1721.