基于阵列式静电传感器的密相气力输送煤粉颗粒运动特性分析

付飞飞 许传龙 王式民 闫 勇

(1 东南大学能源热转换及其过程测控教育部重点实验室，南京210096)

(2 华北电力大学控制与计算机工程学院，北京102206)

超浓相气力输送系统具有复杂的非线性、非平衡动力学特性.由于缺乏对浓相气固两相流流动动力学的了解，给高压浓相气力输送系统的设计及优化运行带来了较大的不确定性［1］.浓相气固两相流中颗粒运动特性的获取有2 种方法:①通过理论分析、数值模拟方法获取;②利用气力输送系统试验得到的颗粒流动信息并结合非线性理论获取.近似熵(approximate entropy，ApEn)作为一种非线性分析方法，从统计学的角度来判断时间过程的复杂性，可以用来表征动力学系统的差异或变化，近些年来，已经广泛应用于流化床流型识别、气液两相流电导波动信号复杂性测度分析以及故障检测等［2-4］.

粉体气力输送过程中，由于颗粒之间以及颗粒与管壁之间的碰撞、分离，颗粒上将产生静电.粉体颗粒静电载有大量的动态信息，是流动特性、输送形态、输送管道几何特性和粉体颗粒等因素内在作用的综合体现［5-7］.近些年来发展起来的环状静电传感器在气固两相流检测与控制中引起了极大关注［8-11］.对于气固两相流中颗粒分布及流型的测量，环状静电传感器却存在不足，这是由于环状静电传感器无法获得颗粒在管道截面的位置及空间局部区域的流动信息.通过在气固两相流系统外部空间位置上布置阵列式静电传感器，获取其临近区域的颗粒信息［12］，这些颗粒静电信息从不同的时间和空间反应了稠密气固流动特性.结合适当的信息处理手段，可以全面地获得颗粒的运动及分布信息.电容层析成像(ECT)技术是一种多相流检测技术，可用于输送管道中的气固、气液两相流等连续相为电介质的工业过程成像.ECT 技术在两相流流动状态检测和参数检测等方面的应用研究已取得一定的成果［13-14］.将ECT 技术与阵列式静电传感器系统二者结合，可深入地了解加压稠密气固两相流颗粒流动状态及其变化规律.

本文首先系统分析了阵列式静电传感器的局部灵敏度分布特性，并在满管流和1/4 流2 种流型下进行了实验验证.之后在高固气比煤粉输送装置上，结合阵列式静电传感器和电容层析成像技术获得了3 种表观气速(5.7，6.9，8.1 m/s)工况下的静电输出信号和管道截面煤粉分布ECT 成像图.结合ECT 成像图，利用FFT 变换和近似熵方法对传感器输出信号进行了分析.

1 阵列式静电传感器局部传感特性分析

图1为阵列式静电传感器探头结构，由8 个电极片、2 个接地圆环保护极板、绝缘管和屏蔽罩等部分组成.其中，8 个电极组成的环状阵列及圆环保护极板紧贴在绝缘管的外壁.

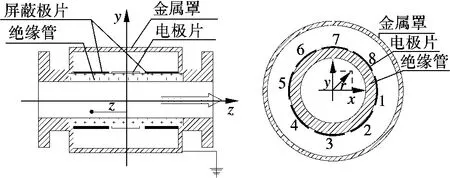
图1 静电传感器探头结构

阵列式传感器的数学模型在文献［12］中已有详细介绍.阵列式静电传感器结构为三维形式，较为复杂，目前尚难以获得模型中静电场的解析解，通常采用数值法进行求解.近些年发展起来的各种电磁场计算软件包使得复杂的静电场计算问题成为可能，本文利用软件Ansoft 完成阵列式静电传感器内部静电场和极片上感应电量的计算.

阵列式静电传感器的灵敏度定义为在敏感空间内，单位点电荷作用下电极上感应电量的绝对值.从阵列式静电传感器的有限元模型可知，灵敏度与点电荷所在的敏感空间位置(x，y，z)有关，即

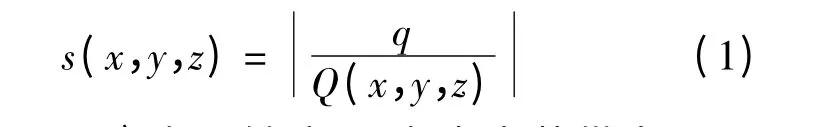
式中，s(x，y，z)为灵敏度;q 为点电荷带电量;Q为点电荷电量为q 时电极上的感应电量.考虑静电传感器阵列电极的轴对称性及三维有限元仿真计算量大等原因，在本实验中模拟5 条较有代表性的点电荷流线(记为a，b，c，d，e，见图2)上的灵敏度分布，并以此来表征阵列式静电传感器的轴向灵敏场分布特性.模型中的管道内径设为10 mm，5 条流线在径向位置上等间隔(间距2 mm)分布，其中c 过圆点.8 个极片的轴向宽度为10 mm，长为6 mm.已知带电颗粒在流线上沿轴向移动时，8 个极片会同时产生感应电量.但为便于分析，只计算电极片1 上的灵敏度分布来表征阵列式静电传感器的轴向灵敏场分布特性，其余7 个电极片都可以旋转到极片1 的位置而得到同样的灵敏度分布.

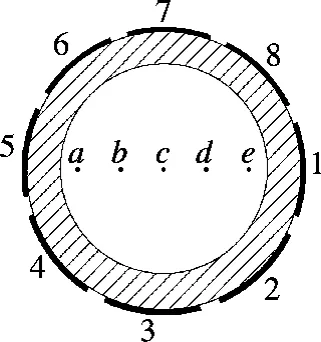
图2 8 极片阵列式静电传感器探头横截面

图3为阵列式静电传感器敏感空间内灵敏度沿轴向的分布.图4为阵列式静电传感器在中心截面(z =0)上的灵敏度分布.从图3可看出，沿轴向位置的增大，同一流线上的灵敏度值逐渐减小，且流线位置离极片越近，其上的灵敏度变化越快.从图4可看出，靠近极片壁面处红色区域代表的灵敏度值最大，离极片越远灵敏度值越小.蓝色代表的最小值只有红色代表的最大值的0.1 倍.结合灵敏度的轴向分布和截面分布，阵列式静电传感器单电极片灵敏场的空间分布具有局部敏感特性.

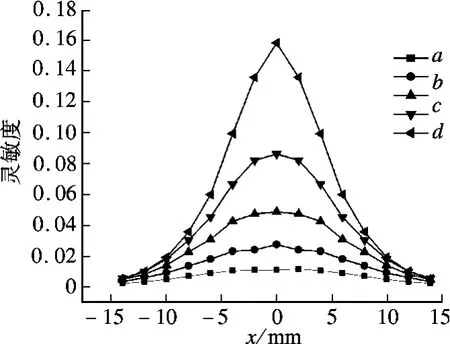
图3 阵列式静电传感器灵敏度沿轴向的分布

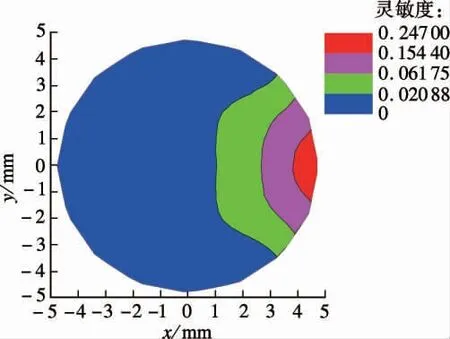
图4 阵列式静电传感器中心截面灵敏度分布

2 近似熵理论

近似熵方法是一种度量时间序列随机性的非线性统计方法［15］.对数据长度为N 的时间序列{x(i)}，重构m 维相空间，其中的矢量y(i)为

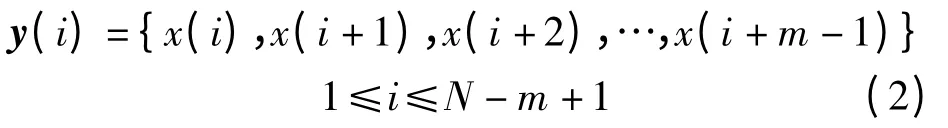
式中，m 又称为窗口长度.定义矢量y(i)与y(j)之间的距离d［y(i)，y(j)］为各矢量之间的最大距离，即

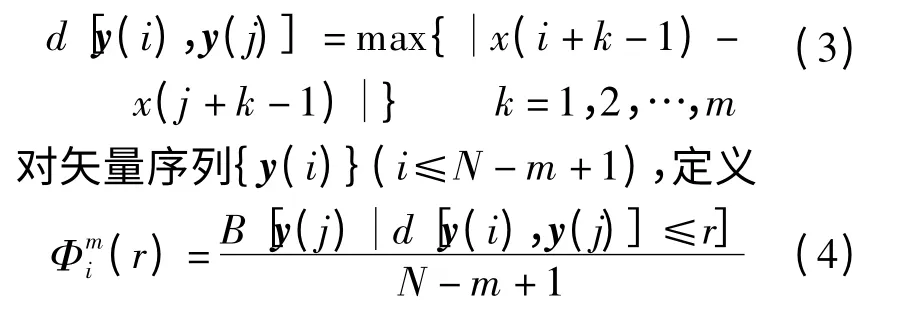
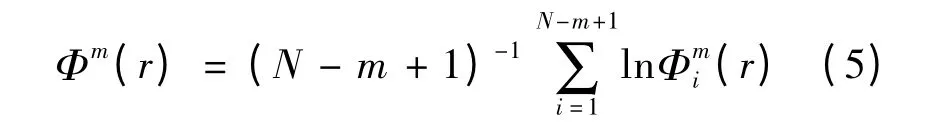
式中，Φm(r)表示矢量序列{y(i)}的平均自相关程度.m 越大，相空间中的状态点越稀，关联机会越小，因而(r)和Φm(r)都随m 增大而变小，对于Φm(r)，其偏差可用下式表示:

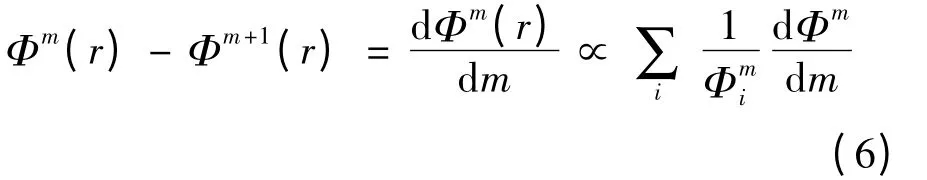
对于不同信号，式(6)的结果会有很大差别.白噪声均匀充满整个相空间各维不大，但Φm极小，因而随着m 增大，Φm(r)－Φm+1(r)→∞.对于规则信号，当m 增大到一定程度后，吸引子全部被打开，Φm便不再随m 增大而增大，即接近于0.因此，可以用Φm－Φm+1刻画系统随机性的程度，近似熵值Eap可定义为

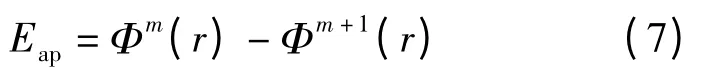
熵值越大，表明时间序列越具有随机性或不规则性，其非周期性越强，复杂度越高;熵值越小，表明数据周期性越强，复杂度越小.

3 实验装置

图5为高压浓相气力输送实验系统，主要由气源系统、储料罐系统、输送管道系统、测量传感器及数据采集系统4 部分组成.高压气体经过缓冲罐分3 路经流量计向输送系统提供冲压风、流化风和补充风.发料罐和收料罐容积均为0.648 m3，输送管为内径10 mm 的不锈钢管，总长53 m.接收罐的支座上布置了CHJL2 型荷重变送器.流化风、充压风和补充风采用AM-1521Q 型金属管浮子流量计测量.缓冲罐气源维持在4 MPa 左右.输送载气为CO2，输送煤粉为云南褐煤.

ECT 系统由传感器探头、数据采集系统和图像重建程序3 个基本部分组成，最高成像速度为74 帧/s，分辨率为32 ×32 像素.ECT 系统与阵列式静电传感器并列安装在同一水平输送管道中.静电传感器的结构尺寸与上述数值模型的结构尺寸一致.静电传感器系统的数据采集部分由电流放大电路、PCI9112 采集卡和计算机构成.在软件的控制下，可以实现8 通道同时采集，本实验中静电传感器输出信号的频率范围在500 Hz 以内，因此每通道的采样频率设定为1 000 Hz.

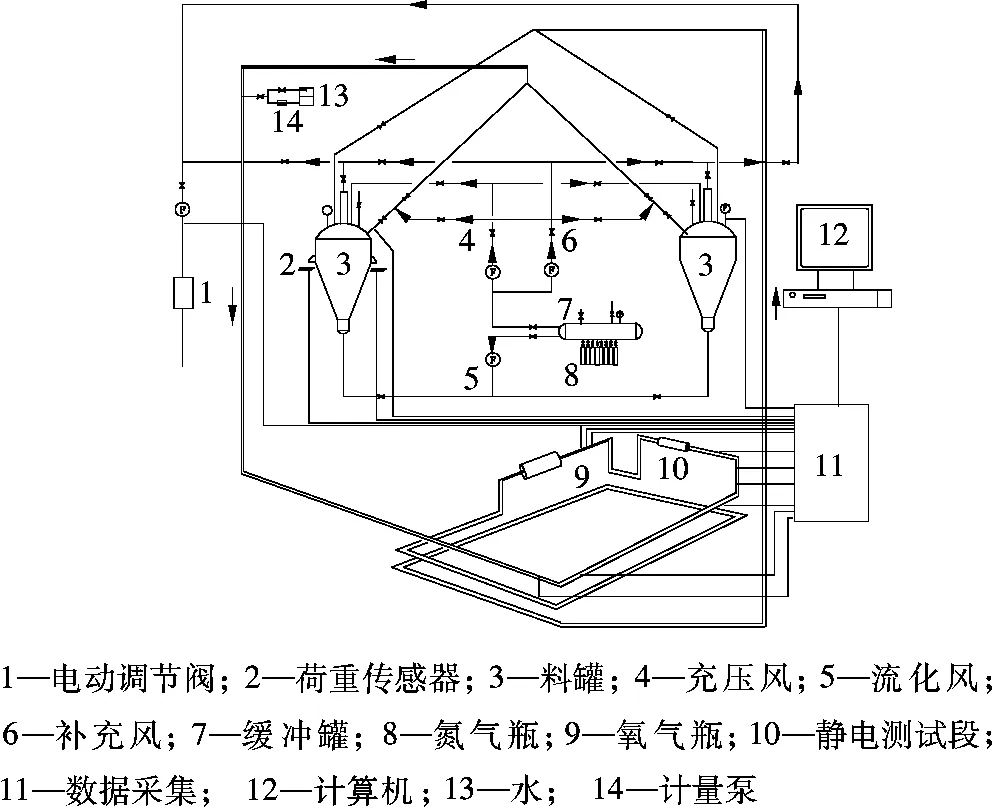
图5 高压浓相气力输送实验台系统图

4 实验结果与讨论

4.1 阵列式静电传感器局部传感特性验证

为了验证阵列式静电传感器的局部传感特性，设计了简易的重力输送试验装置.颗粒在自身重力的作用下由料斗进入管道，再进入静电传感器和电容传感器测试探头.输送管段可垂直或者倾斜放置，可实现1/4 流和满管流2 种流型.实验用的固体颗粒是直径为1 mm 的玻璃珠，管道半径为25 mm.图6为1/4 流ECT 成像及能量分布(第2，3 和4 s 的静电数据)，其中极片相对位置如图2所示.由图6(a)可见，截面煤粉所占面积约为管道截面面积的1/4，且极片3 和4 附近颗粒浓度最大(深色代表该处颗粒密集).从图6(b)可看出，极片3 和4 上的静电信号能量大于其他6 个极片上的信号能量.这证明了阵列传感器极片的灵敏度具有局域性，靠近极片的区域具有较高的灵敏度.图7为满管流的ECT 成像图及8 极片的静电信号能量分布.与图7对比发现，静电信号能量值波动平缓并在能量均值(值为1.94)处上下波动，尽管极片7 附近的颗粒浓度相对较低(见图7(b))导致了其上的静电信号能量值较小.因此，阵列式静电传感器的输出信号的能量分布可有效地反应管道截面上颗粒的分布特性.

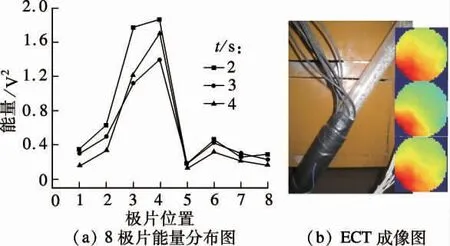
图6 1/4 流ECT 成像及能量分布

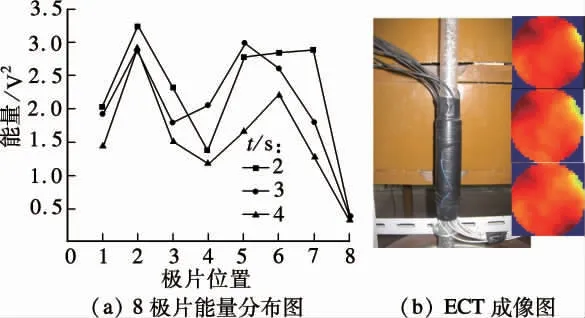
图7 满管流ECT 成像及能量分布

4.2 气力输送实验

在表观气速为5.7，6.9 和8.1 m/s 的3 个工况下进行了气力输送实验.图8为3 个工况下管道截面煤粉分布的ECT 成像图.在水平管气力输送过程中，因受重力影响，煤粉的浓度分布呈不对称性，管下部浓度较高，上部浓度较低.从成像图中可看出，3 个工况下煤粉的输送连续性均较好，煤粉在管道截面的分布随时间变化较小.工况3 下浓相区与稀相区几乎没有分界，此时煤粉的悬浮性及分布均匀性最好.但是ECT 成像图只能反映管道截面煤粉的分布特性以及颗粒的宏观运动特性，却无法反映颗粒随机运动的本质特征.

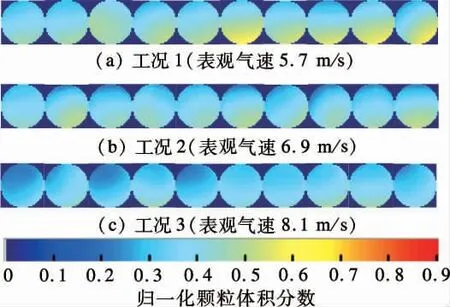
图8 3 种工况下的ECT 成像图

静电传感器输出信号频域特征与其敏感区内颗粒带电量、带电颗粒轴向平均速度和颗粒径向分布的变化密切相关.颗粒带电量增加导致频域幅值增加，带电颗粒轴向速度增加导致主峰频率值增大，而颗粒的径向运动也会对频率特性产生非线性的影响［11-12］.颗粒在管道中运动时，受到气流的曳引作用、颗粒与颗粒及颗粒与管壁间的碰撞作用力以及自身重力等，这些力的共同作用使得颗粒的运动非常复杂，近似为随机运动.近似熵值可以定量分析随机运动的程度.近似熵值越大，颗粒运动的复杂性越大，随机性越强.表1为8 极片上近似熵值、主峰值频率及主峰值频率对应幅值随表观气速的变化规律.可看出，随表观气速的增大，主峰值频率对应的幅值大致有减小的趋势.这是因为表观气速增大时，粉体的质量流量减小，碰撞产生的静电总量减小，导致传感器输出信号的能量减小.但近似熵值和主峰值频率随表观气速的增大没有一致的变化规律.

表1 阵列传感器8 极片上静电输出信号随表观气速增大的规律

从图8中看到，极片2 和3 处于浓相区，极片6和7 处于稀相区，极片1，4，5，8 处于波动区域.由于波动区颗粒分布随机变化，极片1，4，5，8 上静电信号的分析结果不确定，对比性差(见表1).因此本文中采用浓相区极片2，3 和稀相区极片6，7 上静电信号的频域及时域特征来描述浓相区和稀相区颗粒运动特征.

图9为稀相和密相区静电信号主峰值频率与表观气速之间的关系.随着表观气速的增加，极片2，3 上的静电信号主峰值频率一致增大，表明浓相区的颗粒轴向平均速度增大，颗粒径向运动波动相对不剧烈并且其对输出信号频谱特性造成的非线性影响不明显.极片6，7 上的静电信号主峰值的频率虽然总体有增大的趋势，但其间有减小的变化过程，说明稀相区颗粒的径向运动相对剧烈，导致传感器输出信号的主峰值频率呈非线性增长.在湍流运动中，颗粒浓度与颗粒的湍动能有关［16］.当表观气速为5.7 m/s 时，雷诺数(Re)大于2 ×105，已经达到湍流状态.湍动能越大，表明颗粒在径向上的波动越剧烈.尽管当表观气速增大时，颗粒速度增大是主要的变化，但稀相区颗粒速度在径向上的波动也足够明显，以至于其对静电信号主峰值频率的增长造成了非线性的影响.

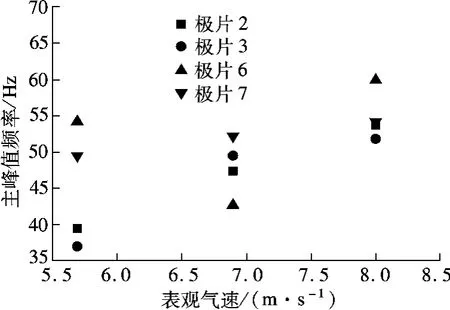
图9 静电信号主峰值频率随表观气速的变化规律

图10为极片2，3 和极片6，7 上的输出信号近似熵值与表观气速之间的关系.表观气速增大时，极片2，3 上输出信号的近似熵值一致减小而极片6，7 上输出信号的近似熵值一致增大，但前者始终大于后者.密相区的颗粒浓度大，颗粒碰撞频率大于稀相区.实际上，静电传感器输出信号的近似熵值不完全表征颗粒运动的复杂性，同时它还与颗粒电荷在轴向和径向上的分布梯度以及电荷随时间的变化率等因素有关.显然，在浓相区，颗粒电荷分布的梯度以及随时间的变化率更随机.尽管稀相区的颗粒的湍流会导致颗粒运动复杂，但是其静电信号的复杂性还是低于浓相区.但当表观气速增大时，浓相区颗粒浓度减小，颗粒碰撞频率降低，导致稀相区和浓相区的颗粒运动复杂性之间的差距减小.对照ECT 成像图，还发现管道煤粉输送的悬浮性与极片2，3 和极片6，7 上输出信号的近似熵值之差有对应关系:差值越小，煤粉的输送悬浮性越好.

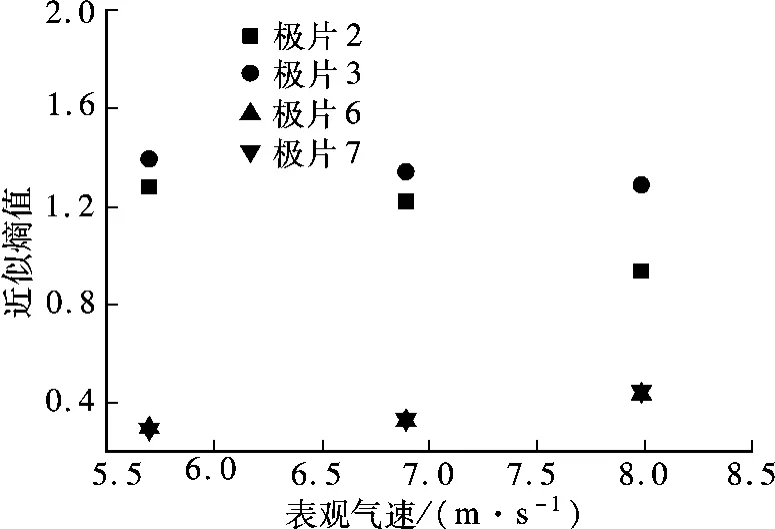
图10 静电信号近似熵值随表观气速的变化规律

5 结语

在加压密相气力输送实验装置上，结合ECT技术，利用FFT 变换和近似熵方法分析了密相气固两相流阵列静电波动信号.结果表明:阵列式静电传感器可利用自身的阵列结构及灵敏度分布特性，获取阵列中各个单传感器灵敏区的颗粒流动的静电信息，从而全面地得到颗粒的运动及分布信息.当表观气速增大时，浓相区静电信号的主峰值频率一致增大，而稀相区静电信号的主峰值频率非线性增长，表明表观气速增大导致颗粒运动速度增大，并且稀相区颗粒径向速度波动明显;稀相区和浓相区的颗粒运动复杂性程度越接近，煤粉的输送悬浮性越好.同时，随表观气速的增大，浓相区静电信号的近似熵值减小，稀相区静电输出信号的近似熵值增大，但浓相区的近似熵值一直大于稀相区的近似熵值，对应ECT 成像图，发现随两者差值的减小，管道内煤粉分布越均匀，输送悬浮性越好.

References)

［1］梁财.高压超浓相煤粉气力输送流动特性研究［D］.南京:东南大学能源与环境学院，2007.

［2］杨进，文玉梅，李平.基于相关分析和近似熵的管道泄漏声信号特征提取及辨识方法［J］.仪器仪表学报，2009，30(2):272-278.

Yang Jin，Wen Yumei，Li Ping.Feature extraction and identification of leak acoustic signal in water distribution pipelines using correlation analysis and approximate entropy［J］.Chinese Journal of Scientific Instrument，2009，30(2):272-278.(in Chinese)

［3］栗然，陆凤怡，徐宏锐，等.基于局域波与近似熵的负荷分析方法［J］.中国电机工程学报，2010，30(25):51-58.

Li Ran，Lu Fengyi，Xu Hongrui，et al.Novel approach for load analysis based on local wave and approximate entropy［J］.Proceedings of the CSEE，2010，30(25):51-58.(in Chinese)

［4］林萍，王晓萍，陈伯川，等.近似熵的性质及其在气固流化床复杂性研究中的应用［J］.高校化学工程学报，2004，18(3):281-286.

Lin Ping，Wang Xiaoping，Chen Bochuan，et al.Character of approximate entropy and its application in the complexity measurement of gas-solid fluidized bed［J］.Journal of Chemical Engineering of Chinese Universities，2004，18(3):281-286.(in Chinese)

［5］Matsusaka S，Masuda H.Electrostatics of particles［J］.Advanced Powder Technology，2003，14(2):169-179.

［6］Nifuku M，Katoh H.A study on the static electrification of powders during pneumatic transportation and the ignition of dust clouds［J］.Powder Technology，2003，135-136:234-242.

［7］Masuda H，Komatsu T，Mitsui N，et al.Electrification of gas-solid suspensions flowing in steel and insulatingcoated pipes［J］.Journal of Electrostatics，1977，2(4):341-350.

［8］Qian Xiangchen，Yan Yong，Shao Jiaqing，et al.Quantitative characterization of pulverised coal and biomass-coal blends in pneumatic conveying pipelines using electrostatic sensor arrays and data fusion techniques［J］.Measurement Science and Technology，2012，23(8):1-8.

［9］Gajewski J B.Non-contact electrostatic flow probes for measuring the flow rate and charge in the two-phase gassolid flows［J］.Chemical Engineering Science，2006，61(7):2262-2270.

［10］Gajewsk J B.Electrostatic nonintrusive method for measuring the electric charge，mass flow rate，and velocity of particulates in the two-phase gas-solid pipe flows—its only or as many as 50 years of historical evolution［J］.IEEE Transactions on Industry Applications，2008，44(5):1418-1430.

［11］Xu Chuanlong，Wang Shimin.HHT analysis of electrostatic fluctuation signals in dense-phase pneumatic conveying of pulverized coal at high pressure［J］.Chemical Engineering Science，2010，65(4):1334-1344.

［12］Xu Chuanlong，Li Jian，Wang Shimin.Investigations into sensing characteristics of electrostatic sensor arrays through computational modeling and practical experimentation［J］.Journal of Electrostatics，2012，70(1):60-71.

［13］杨道业，周宾，王式民.电容层析成像在高压浓相煤粉气力输送中的应用［J］.化工学报，2009，60(4):892-897.

Yang Daoye，Zhou Bin，Wang Shimin.Application of electrical capacitance tomography in dense-phase pneumatic conveying of pulverized coal under high pressure［J］.Journal of the Chemical Industry and Engineering Society of China，2009，60(4):892-897.(in Chinese)

［14］Cong Xingliang，Guo Xiaolei，Gong Xin，et al.Experimental research of flow patterns and pressure signals in horizontal dense phase pneumatic conveying of pulverized coal［J］.Powder Technology，2011，208(3):600-609.

［15］Pincus S.Approximate entropy(ApEn)as a complexity measure［J］.CHOAS，1995，5(1):110-117.

［16］Sinclair J L，Jackson R.Gas-particle flow in a vertical pipe with particle-particle interactions［J］.AIChE Journal，1989，35(9):1473-1486.