圆筒型无铁心永磁直线电机空载磁场解析计算

董剑宁 陈艳龙 黄允凯 金 龙

(东南大学电气工程学院，南京210096)

直线电机无需借助机械齿轮、滚珠丝杠等转换装置即可实现直线运动，具有结构简单、动态性能好等优点，近年来在交通运输、伺服控制、建筑工程、医疗器械等领域获得越来越广泛的应用.

高精度伺服应用要求永磁直线电机具有尽可能低的定位力矩和单边力矩.因此，采用无槽动子的圆筒形永磁直线电机成为此类应用的首选.这种电机定子永磁体分为表贴式和内嵌式2 种:前者沿径向充磁，贴装在磁轭的表面;后者沿轴向充磁，嵌在铁心之间［1－2］.为进一步降低动子惯量以提高电机加速能力，可采用无铁心动子结构［3］.此时，为增强主磁场，定子一般采用Halbach 阵列结构或内嵌式的聚磁结构［4］.

文献［5］提出一种定、动子均无铁心的圆筒型无铁心永磁直线电机结构.其定子由轴向充磁的圆柱型永磁体组成，相邻永磁体充磁方向相反，且紧贴在一起，中间无铁磁性极靴.与普通的定子无铁心圆筒型直线电机相比，该电机对永磁磁通的利用率更高，对动子偏心的敏感度更低，运动过程中绕组电感变化更小，因而具有更高的效率和控制精度［6］.目前，这种结构的圆筒型无铁心永磁直线电机已在纳米级高精度伺服系统中获得应用［7］，但国内外关于此种电机电磁场分析的文献较少.

为准确分析直线电机的电磁场分布，优化电机设计，国内外学者提出了多种方法.其中最常用的是等效磁路法［8］，该方法简单易用，但存在模型不准确的问题，在漏磁较大或磁路复杂时尤为严重.采用有限元法［9］可以对复杂边界、多种媒介以及非线性、饱和等问题进行有效处理，具有明显的优越性，但前处理和计算耗时较长，不适合在电机优化设计的迭代计算中使用，一般用于确定各项尺寸参数后的电磁性能核算.使用解析法计算电磁场可以克服上述2 种方法的缺点，其特点是计算时间短，且不需要复杂的前处理，能直观地表述各项参数对磁场分布的影响，以便调整参数进行优化设计.但解析法不能考虑铁心磁导率的非线性，仅适用于磁路饱和程度低的场合.文献［1，10－11］均为解析法在直线电机电磁设计中的典型应用.

本文所研究的圆筒型无铁心永磁直线电机定、动子上均无铁心，磁路线性且具有高度对称性，非常适合解析法的应用.本文首先在圆柱坐标系下采用磁荷模型计算出单个圆柱形永磁体的磁场分布，再应用叠加原理得到整个电机的气隙磁场分布.之后在空载磁场的基础上推导出电机反电势和推力表达式.最后通过有限元软件对解析计算结果进行验证，证明了该解析法的正确性.

1 磁场计算

1.1 磁荷模型

在无电流的永磁体和空气区域，磁感应强度矢量B 和磁场强度矢量H 满足下式:

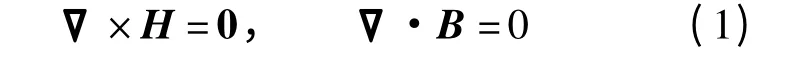
根据矢量场的亥姆霍兹定理，存在标量φm，使

再将永磁体本构关系B =μ0(H +M)代入式(1)、(2)可得

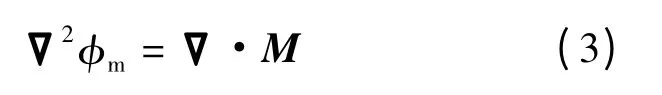
式中，M 为永磁体的磁化矢量.对式(3)中的拉普拉斯算子应用格林函数，可解得

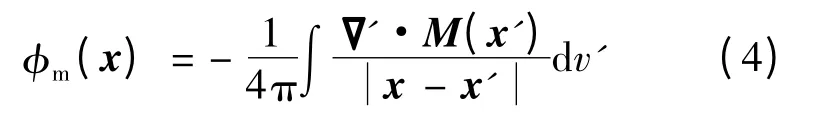
式中，x 为场点的位置矢量;x′为源点的位置矢量.M 仅存在于永磁区域内，因在永磁区域表面M 突变为0，式(4)需写为

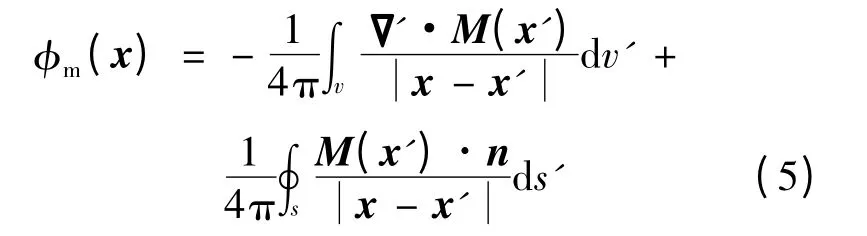
式中，v′为永磁区域;s′为v′的表面;n 为s′外法方向上的单位矢量.参考电荷模型，可假设在永磁体内存在体密度ρm=－▽·M，表面密度σm=M·n的磁荷.由此可推得，空气中x 处的磁密为［12］

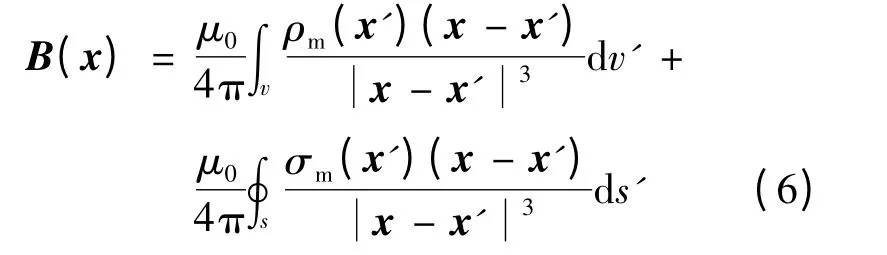
1.2 空载磁场求解

对于组成图1中圆筒型无铁心永磁直线电机定子的某个轴向充磁的圆柱形永磁体(见图2)而言，仅左右两个圆形底面上存在密度为M 的磁荷.仅考虑右底面上的磁荷，由其引起的φm为的坐标，ρ，φ 为场区点的坐标.对使用文献［13］中的积分变换，可得

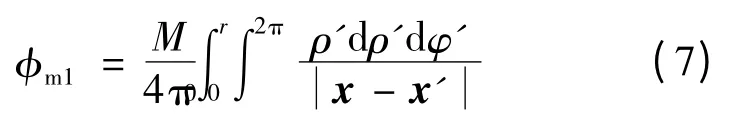
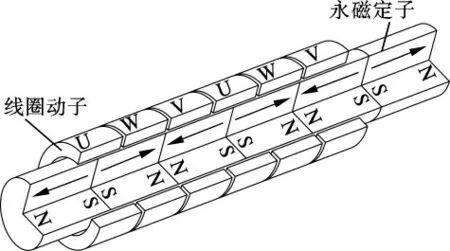
图1 圆筒型无铁心永磁直线电机结构

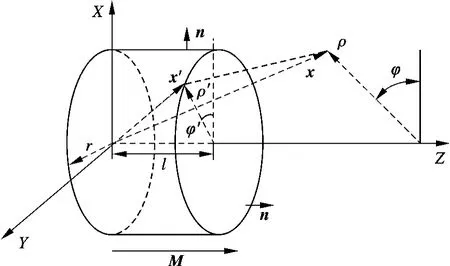
图2 单个轴向充磁的圆柱形永磁体模型

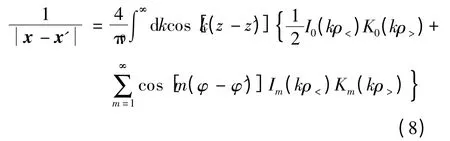
式中，Im，Km分别为第一类和第二类m 阶虚宗量的贝塞尔函数;ρ＞(ρ＜)为ρ 和ρ′中的较大(小)者.由磁场的轴对称性知，φm1与φ 无关，为简化计算，可令φ=0.将式(8)代入式(7)，有

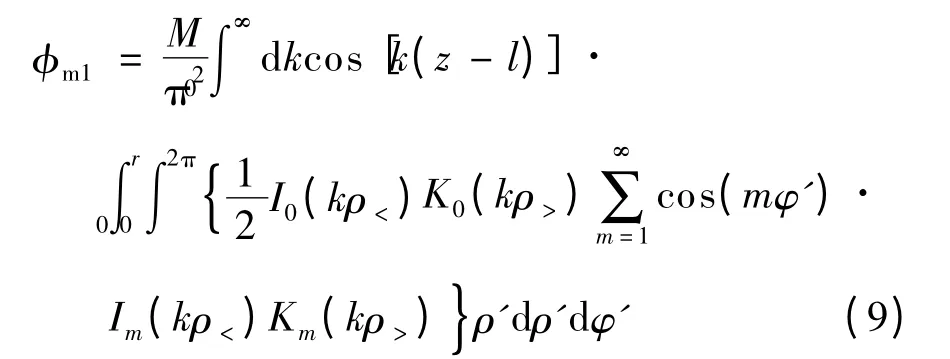
式中，l 为圆柱形永磁体的长度.由于其中二重积分的第2 项为0，式(9)可简化为

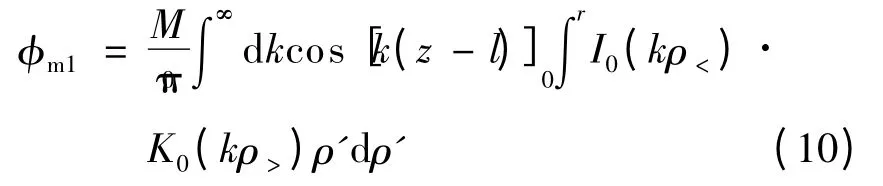
利用虚宗量的贝塞尔函数的性质［14］，对式(10)中的第2 个积分进行处理，可得在ρ ＞r 的区域(即空气)内，有

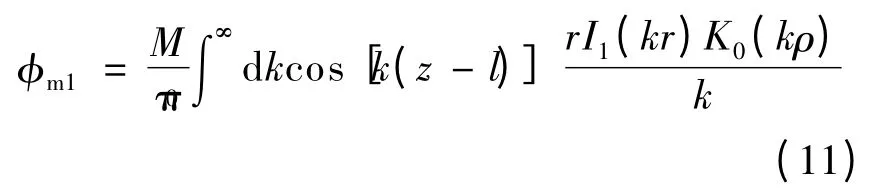
对其求梯度，可得到空气中磁通密度的径向和轴向分量分别为

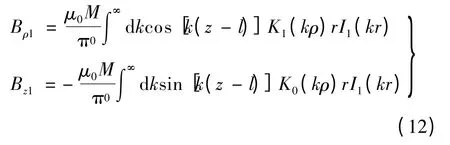
同样可求出由永磁体的左底面上的磁荷引起的磁密分量为

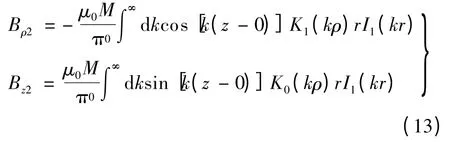
由于磁路线性，可直接利用叠加原理，得到由n 个永磁体组成的圆筒型无铁心永磁直线电机定子的空载磁密为

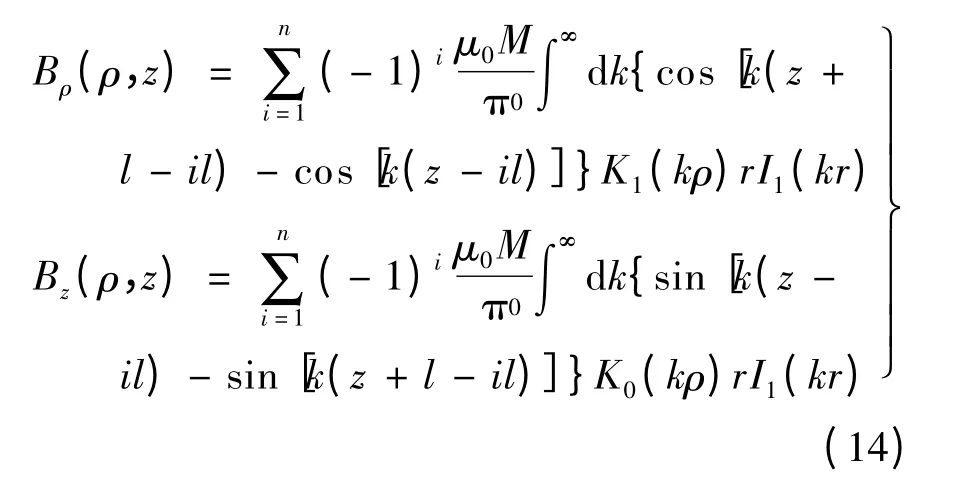
2 反电势与推力计算

圆筒型无铁心永磁直线电机的动子绕组线圈轴对称地环绕在定子外，每相绕组由若干组线圈串/并联而成.图3为动子绕组示意图，其中Rco为线圈的外半径，Rci为其内半径，wc为每组线圈宽度.

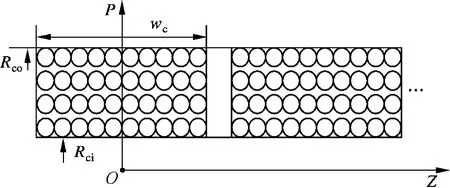
图3 动子绕组示意图

根据法拉第电磁感应定律，动子沿Z 轴作直线运动时，每根环形线圈内都会切割径向磁场感应出反电势.根据空载磁场计算结果推导出每根线圈内产生的反电势，再将同相线圈的反电势相加即可得到相反电势.但这样计算过程复杂，耗时长.为简化计算，可假设所有线圈均集中在平均半径处.如图3所示，设某组线圈轴线所在位置为z，则该组线圈区域内的径向磁密平均值为

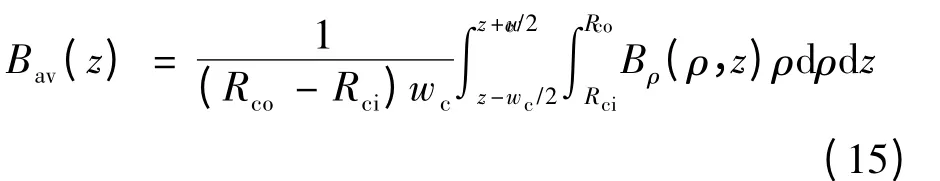
该组线圈在该位置时的反电势为

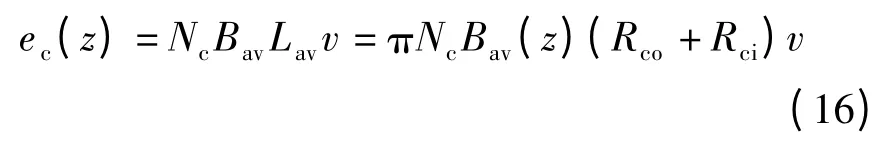
式中，v 为动子运动速度;Nc为该组线圈的串联匝数;Lav为每匝线圈的平均长度.将同相的每组线圈中的反电势相加，即可得到每相绕组反电势波形.

动子上的推力是由电枢电流与空载磁场相互作用而产生的洛仑兹力.同样认为线圈集中在平均磁密处，可得一组线圈的推力为

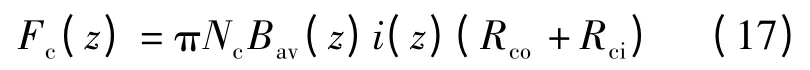
将所有线圈组上的推力相加，即可得到总的动子推力.

3 结果对比与分析

使用以上解析模型分析了某型号圆筒型无铁心永磁直线电机，计算了其空载磁场、反电势和动子推力.该型号电机的主要参数如表1所示.

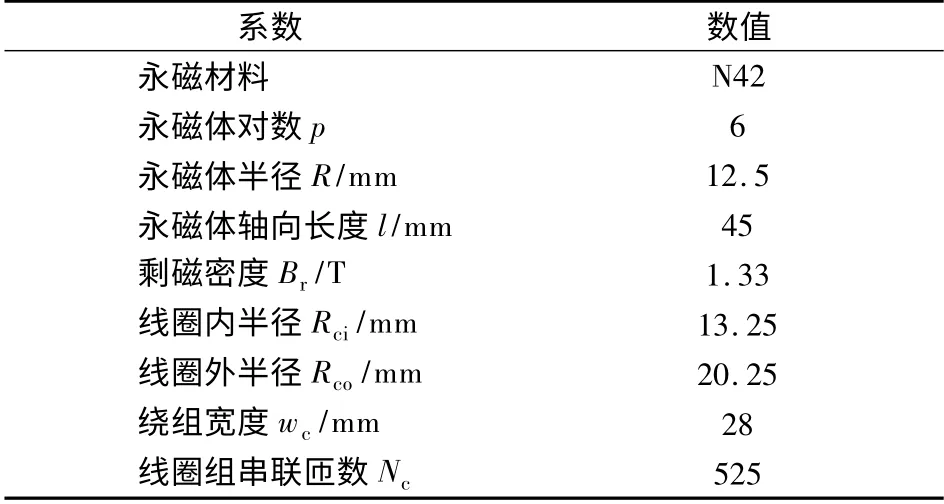
表1 某型号圆筒形无铁心永磁直线电机主要参数

为验证以上解析计算方法的正确性，建立了该电机的二维轴对称有限元模型，图4给出了有限元法计算出的空载磁场分布结果.和径向分量的有限元法和解析法计算结果.可看出随着轴向距离的增加，空载磁密呈周期性变化.受边端效应影响，边缘处磁密快速下降.解析法相对于有限元法的最大偏差出现在径向磁密最大的位置，但此时误差也在5%以内.出现偏差的主要原因是最大磁密处对应的实际磁化强度要低于解析模型中使用的剩余磁化强度.

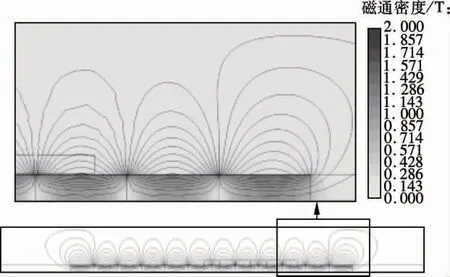
图4 圆筒形无铁心永磁直线电机的磁场分布

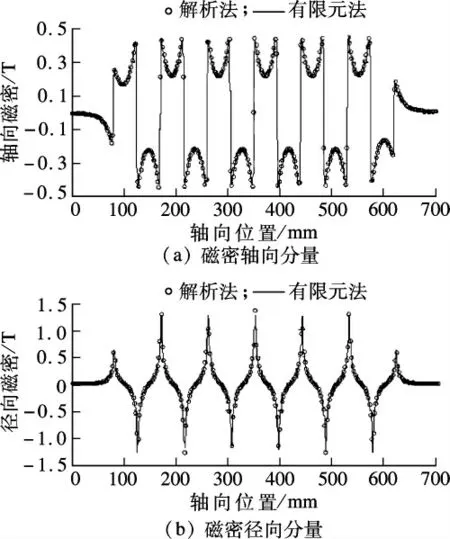
图5 ρ=13 mm 处解析法与有限元法磁密计算结果对比

图6给出了2 种方法计算出的动子以1 m/s速度沿轴向运动时U 相绕组中的反电势波形，可见2 种计算方法所得结果非常接近，最大误差为7%.二者存在偏差的原因除磁化强度的偏差外还有解析模型中对线圈所作的平均化处理.

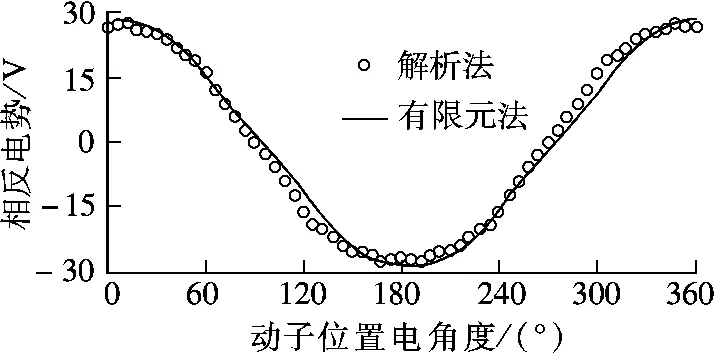
图6 动子运动速度为1 m/s 时U 相绕组的反电势

在绕组中通入有效值为1.3 A 的三相对称电流，并使电流位于q 轴上，得到如图7所示的动子推力曲线.由图可知，解析法与有限元法计算出的推力波形接近.解析法所得推力平均值为77.8 N，有限元法结果为79.0 N，两者偏差小于2%.

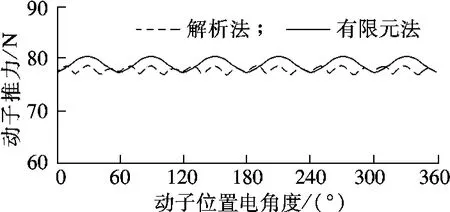
图7 一个电周期内动子受力曲线

图8对比了负载状态下，ρ=13 mm 处，A 相线圈电流达到幅值时对应极面下的磁密波形以及相同位置的空载磁密波形.2 种波形均由有限元分析得到.由图可见，2 种波形非常接近，这说明负载电流对电机磁场的影响非常小，这也是该种电机的优点之一.

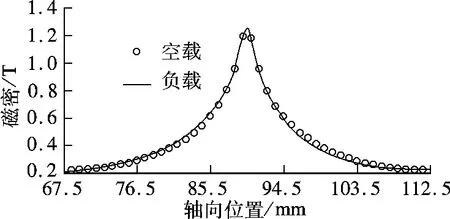
图8 空载与负载时一个极面下的磁密波形

4 结语

本文应用磁荷法在圆柱坐标系下导出了圆筒型无铁心永磁直线电机的空载磁场解析计算模型，给出了空载磁场轴向和径向分量的解析公式.在此基础上，对线圈区域进行平均化处理，求出电机相反电势和推力的解析公式.之后利用此解析方法分析了某型号圆筒型无铁心永磁直线电机，所得结果与有限元法所得结果进行了对比，验证了解析法的正确性.本文所提出的解析计算方法适用于该种电机的电磁设计，对于其他永磁直线电机的理论分析也有参考价值.

References)

［1］赵镜红，张晓峰，张俊洪.圆筒永磁直线同步电机磁场和推力分析［J］.电机与控制学报，2010，14(1):12－17.

Zhao Jinghong，Zhang Xiaofeng，Zhang Junhong.Field and thrust analysis of tubular permanent magnet linear synchronous motor［J］.Electrical Machines and Control，2010，14(1):12－17.(in Chinese)

［2］王咏菲.圆筒型永磁直线同步电机的电磁场分析与研究［D］.天津:天津大学电气与自动化工程学院，2008.

［3］刘晓.空心式永磁直线伺服电机及其驱动控制系统研究［D］.杭州:浙江大学电气工程学院，2008.

［4］Trumper D，Kim W，Williams M.Design and analysis framework for linear permanent magnet machines［J］.IEEE Transactions on Industry Applications，1996，32(2):371－379.

［5］Ishiyama N.Linear motor equipped with a stator which is easily assembled:US，6040642［P］.2000.

［6］Suzuki A，Yoshida T.Position detection for shaft－type linear motor by measurement of shaft surface magnetic flux［C］//Proceedings of International Conference on Electrical Machines and Systems.Tokyo，Japan，2009:5382917－01－06.

［7］Nippon Pulse Ltd.Linear shaft motor—nippon pulse［EB/OL］.(2011－08－09)［2012－09－06］.http://www.nipponpulse.com.

［8］Mizuno T，Yamada H.Magnetic circuit analysis of a linear synchronous motor with permanent magnets［J］.IEEE Transactions on Magnetics，1992，28(5):3027－3029.

［9］Tomczuk B，Schroder G，Waindok A.Finite－element analysis of magnetic field and electromechanical parameters calculation for a slotted permanent－magnet tubular linear motor［J］.IEEE Transactions on Magnetics，2007，43(7):3229－3236.

［10］Wang J，Howe D，Jewell G.Analysis and design optimization of an improved axially magnetized tubular permanent－magnet machine［J］.IEEE Transactions on Energy Conversion，2004，19(2):289－295.

［11］王淑红，熊光煜.新型筒型永磁动圈式直线电动机气隙磁场解析分析［J］.电工技术学报，2007，22(5):41－46.

Wang Shuhong，Xiong Guangyu.Analysis of air gap field in a new tubular linear PM motor with moving coil［J］.Transactions of China Electrotechnical Society，2007，22(5):41－46.(in Chinese)

［12］Furlani E.Permanent magnet and electromechanical devices［M］.New York:Academic Press，2001.

［13］胡嗣柱，倪光炯.数学物理方法［M］.上海:复旦大学出版社，1989.

［14］Olver F，Lozier D，Boisvert R，et al.NIST handbook of mathematical functions［M］.New York:Cambridge University Press，2010.