不同参数下封闭矩形声腔的结构-声耦合特性分析

王 园 张建润 顾 伟 黎文琼

(东南大学机械工程学院，南京211189)

工程中许多结构如车辆驾驶室、车厢和船舱等，可以近似看成由弹性板围成的声腔结构.对这类声腔结构耦合机理的研究，在噪声与振动主动控制方面有着十分重要的现实意义和工程应用价值.对于由弹性板-声腔组成的系统的振动与声场特性，文献［1-4］提出了弹性板-声腔组成的耦合系统的求解方法.Pan 等［5］利用模态耦合分析法研究了简支板-矩形声腔组成的耦合系统的自由振动特性，重点分析了简支板的模态密度(对应板厚度)、阻尼对耦合系统的影响，但没有考虑声腔的深度和壁面声阻抗对板-声腔耦合系统的影响.Kim 等［6］提出了分析简支板与声腔耦合特性的阻抗-导纳法.靳国永等［7］在Kim 等的研究基础上，将板-声腔耦合系统类比成反馈与前馈控制系统，对简支板与声腔的耦合特性进行了研究，并且详细分析了板厚和声腔深度对第一阶板控模态共振频率的影响，但没有对其他板控模态和腔控模态的影响进行分析.基于弹性板和声腔的耦合特性，国内外学者［8-11］对弹性板封闭声腔内的声场主动控制进行了广泛的研究.综上所述，当声腔深度不变，而弹性板的模态密度和阻尼变化时，板和声腔的耦合特性已得到深入研究;但当声腔参数如声腔深度改变时，板-声腔的耦合特性会发生显著的变化.而目前尚没有文献就声腔参数变化对板-声腔系统耦合特性的影响进行深入研究.

本文在Pan 等［5］对简支板-声腔耦合特性研究的基础上，进一步分析了声腔深度改变对板-声腔系统耦合特性的影响.首先，基于耦合前板和刚性壁面声腔模态参数，利用模态耦合法对板-声腔组成的耦合系统的自由振动特性进行求解，得到反映耦合系统固有属性的模态特征;接着分析了声腔深度对板-声腔耦合系统模态特征的影响，包括系统模态共振频率、模态衰减时间，并详细研究了板模态与声腔模态随声腔深度改变时的耦合过程.

1 分析模型

弹性板-声腔耦合系统模型如图1所示，封闭矩形声腔的尺寸为Lx，Ly，Lz，位于z =Lz处的弹性板的尺寸为Lx，Ly，边界形式为简支;平面波Pin 作用在弹性板上，方位角和仰角分别为θ，α.声腔内声压的波动方程为

式中，p，c0分别为声腔内的声压和声速.声腔内部声场在声腔壁面处的边界条件为

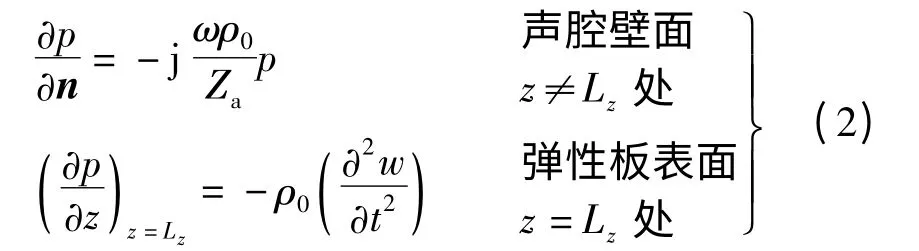
图1 弹性板-声腔耦合系统模型

式中，ρ0为声腔内声场的介质密度;n 为声腔壁面法向;Za为声腔壁面z≠Lz处声阻抗;w(x，y，t)为弹性板法向位移;ω 为角频率.

对于声腔上的弹性薄均质板，在受声腔内外声场激励时，弹性板弯曲振动方程为

式中，定义力的方向指向声腔外为正;ρ，E，μ，h 分别为弹性板的体密度、弹性模量、泊松比和厚度;fp为声腔外作用在弹性板上的总声压，这里指作用在弹性板上的平面声波Pin 和其反射声波之和，并令入射平面波和反射波的声压相等，忽略板向声腔外辐射声对其振动的影响.

利用简正模态振型函数的正交性，刚性壁面声腔内点r 处声压p(r，ω)、无阻尼弹性板σ 点处振动速度v(σ，ω)=jωw(x，y，t)和施加在弹性板上平面波性质的外力fp(σ，ω)，分别可表示为

式中，pq，ve，Fe分别为声腔内声场、板振动速度和外力的模态幅值;φq，se分别为刚性壁面声腔声场分布和无阻尼板振动的振型函数.Pan 等［5］把φN，sM作为分析带有阻尼的弹性板、具有声阻抗的声腔壁面的板-声腔耦合系统的基函数，本文分析也采用此方法，即

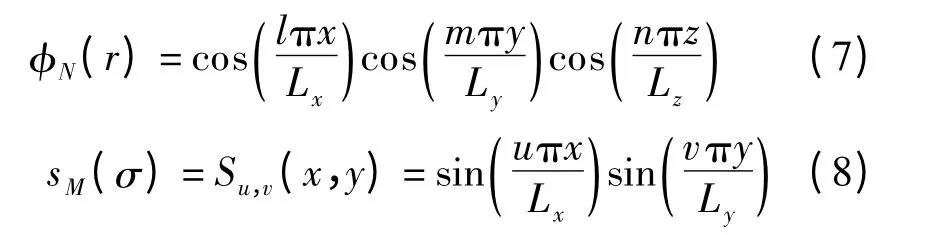
式中，(l，m，n)为N 阶声腔模态的模态序数;(u，v)为M 阶板模态的模态序数.考虑式(2)的声腔壁面边界条件，利用格林函数，式(1)转变为

式中，Af为z =Lz处弹性板表面;Al为z≠Lz处声腔壁面;β 为壁面Al处的声导纳率，β =ρ0c0/Za;Ga为声腔格林函数，即

式中，Gp为板的格林函数.

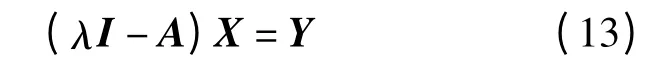
式(13)展开可写成

式中，I 为单位矩阵;λ =－jk;A11和A12分别为(N+M)×(N+M)阶零矩阵和单位矩阵.

式中，kaN=ωaN/c0，kaN，ωaN分别为刚性壁面声腔的第N 阶声模态波数和共振角频率;kpM= ωpM/c0，kpM，ωpM分别为耦合前的第M 阶板模态波数和共振角频率;BN，M为第M 阶板模态和第N 阶声腔模态之间的耦合系数;MpM，MaN为第M 阶板模态和第N 阶声腔模态的模态质量，MpM=ρhΛM，MaN=ρ0ΛN;ηpM，ηaN分别为第M 阶板模态和第N 阶声腔模态的阻尼损耗因子，它们与对声腔壁面导纳率β 积分有关［5］，ηpM=4.4π/(TpMc0)，ηaN=4.4π/(TaNc0)，TpM，TaN分别为第M 阶板模态和第N 阶声腔模态的60 dB 衰减时间.分析时假定所有TpM都相等，TaN都相等.

2 弹性板-声腔耦合特性分析

2.1 模态耦合系数

模态耦合系数BN，M是板和声腔的模态匹配程度，决定板模态和声腔模态间是否耦合.由式(17)可知，耦合系数不为零，板模态(u，v)和声腔模态(l，m，n)必须满足条件:u+l 和v +m 均为奇数.

2.2 传递因子

模态耦合系数决定板模态和声腔模态之间是否耦合，而传递因子决定它们耦合的程度［5］，其中第N 阶声腔模态与第M 阶板模态的传递因子FN，M为

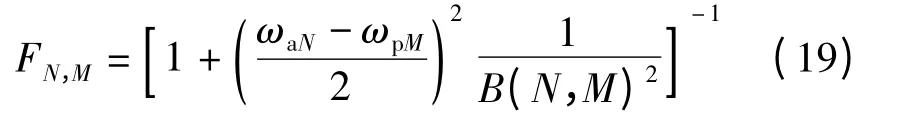
其中

由式(19)和(20)可知，当模态耦合系数BN，M≠0 时，传递因子FN，M≠0，此时第N 阶声腔模态与第M 阶板模态之间的能量传递由以下因素决定:ωaN－ωpM，Lz等.传递因子FN，M趋于0，第N 阶声腔模态与第M 阶板模态之间能量传递也趋于0;而当FN，M≅1，此时板与声腔的模态耦合比较重要，有大的能量传递出现.

2.3 耦合系统的固有频率和模态衰减时间

板-声腔耦合系统模态存在腔控模态和板控模态2 种.对于腔控模态，耦合系统的大部分能量储存在声腔声场中，板控模态［5］与之相反.

由上面的理论分析可知，当耦合系统不受激励时，即Y=0，式(14)变成求解耦合系统的自由振动特征问题，可得到2(N+M)个特征值λL和其共轭值λ*L，其中L =1，2，…，N+M，耦合后的第L 阶共振频率和模态衰减时间分别为fL= Im(λL)c0/(2π)，TL=6.91/(Re(λL)c0).当有外部激励时，即Y≠0，对式(14)进行求解，得到的向量X 就是耦合系统受激励时的板振动和声腔声场的模态坐标，代入式(4)和(5)即可求得声腔声压和板振动速度的分布.

得到声腔内声场和板振动的模态坐标后，声腔内声势能EaN和板振动能量EpM为

式中，ΛaN和ΛpM分别为N ×N 维和M ×M 维对角矩阵，对应的对角线上的元素分别为ΛN和ΛM.

3 理论计算与分析

根据图1的板-声腔耦合系统模型，设顶面是7 mm 厚的铝板，密度为2 770 kg/m3，杨氏模量为71 GPa，泊松比为0.33.声腔内空气密度为1.21 kg/m3，声速为344 m/s.

3.1 声腔深度对板-声腔耦合特性的影响

矩形声腔声场模态的共振频率为

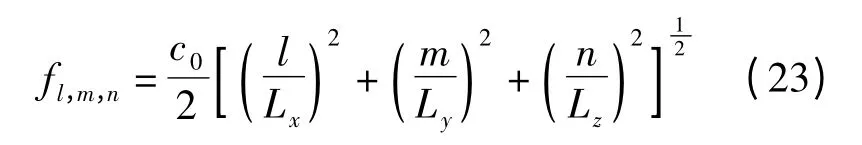
由式(23)可知，声腔模态序数中n≠0 的共振频率fl，m，n随着声腔深度Lz而改变.再由式(19)可知，当声腔模态和板模态间耦合系数不为零时，声腔和板的模态间传递因子分为2 种情况:①当声腔模态序数n≠0 时，传递因子由对应耦合前共振频率差决定，差值越小，耦合越强;②当声腔模态序数n=0 时，其共振频率不随声腔深度变化，此时传递因子由声腔深度来决定，其随声腔深度增大而减小.

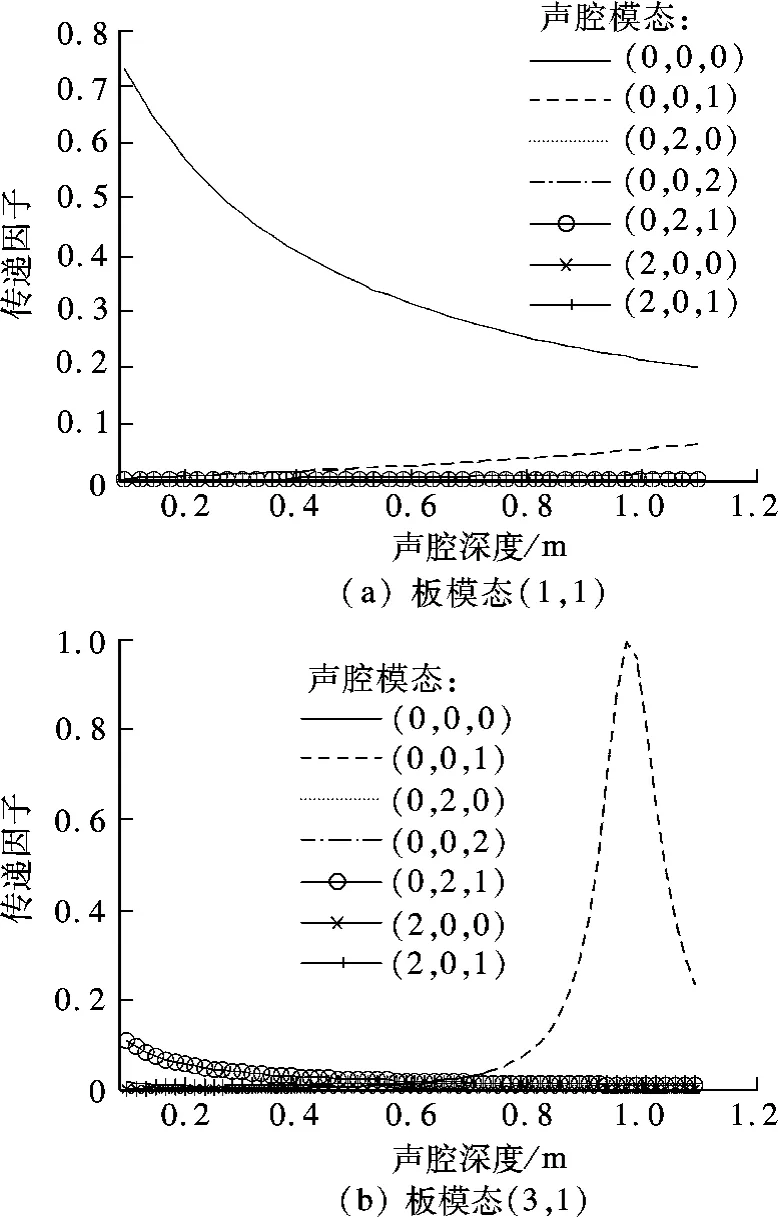
图2 板模态和声腔模态随声腔深度变化的传递因子(TaN =15 s，TpM =0.5 s)

图2(a)为板模态(1，1)和声腔模态随声腔深度变化的传递因子，只有声腔模态(0，0，0)和板模态(1，1)在分析的声腔深度范围有大的传递因子，但值小于1，并且随着声腔深度的增加，传递因子逐渐减小;由于此时声腔模态序数n =0，传递因子由声腔深度决定.图2(b)中，只有声腔模态(0，0，1)和板模态(3，1)在声腔深度0.99 m 处传递因子约为1，其他声腔模态和板模态(3，1)的传递因子都远小于1.板模态(1，1)与声腔模态(0，0，0)之间的传递因子由声腔深度来决定，而板模态(3，1)和声腔模态(0，0，1)之间的传递因子则由对应耦合前共振频率差决定.

由图3可知，前5 阶板控模态的共振频率随声腔深度的增加，逐渐趋向于耦合前的板共振频率.这是由于此声腔深度范围内与板模态起主要耦合作用的声腔模态序数n =0，传递因子大小由声腔深度决定，对应图2(a)中传递因子随声腔深度的增加逐渐变小(板模态(1，2)、(2，1)、(1，3)、(2，2)与此相似)，并且在所分析的声腔深度范围内都小于1，即板模态和声腔模态间耦合逐渐变弱，并且无强耦合.而随着声腔深度的变化，板控模态(2，3)、(3，1)、(1，4)的共振频率出现向高频跃变现象，其中板控模态(3，1)的共振频率跃变出现在0.99 m 的声腔深度处，对应图2(b)中传递因子约为1 的声腔深度，即在此深度，板和声腔的模态耦合前共振频率接近相等.与板控模态(3，1)一样，在板控模态(2，3)、(1，4)的共振频率出现跃变的声腔深度处，传递因子约为1.

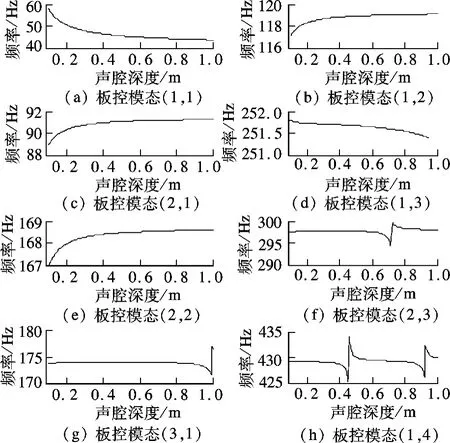
图3 声腔深度对板控模态共振频率的影响(TaN =15 s，TpM =0.5 s)

对应图3中板控模态的共振频率变化情况，图4中前5 阶板控模态衰减时间TL随声腔深度的增加逐渐趋于恒定值;而板控模态(2，3)、(3，1)、(1，4)的衰减时间则出现了峰值，这是由于在出现峰值处耦合最强，并且有大的能量传递.

图4 声腔深度对板控模态衰减时间TL 的影响(TaN =15 s，TpM =0.5 s)

3.2 弹性板模态与声腔模态耦合机理分析

由图2(b)知，当声腔深度在0.956～1.03 m之间时，板模态(3，1)和声腔模态(0，0，1)的传递因子出现约为1 的峰值，其余传递因子值远小于1，满足强耦合分析条件.分析时令作用在板表面处平面波Pin 的幅值Pin0为2 Pa，仰角α 和方位角θ均为0°，激励频率分别为腔控模态和板控模态的共振频率.

当板模态(3，1)和声腔模态(0，0，1)的传递因子约为1 时，图5(a)中腔控模态(0，0，1)与板控模态(3，1)的板振动能量与声腔内声势能之比接近相等;距离能量比相等处越远，能量比相差越大.图5(b)显示随着声腔深度增加，与图5(a)相同，板控模态(3，1)的衰减时间先增加到峰值点再减小，而腔控模态(0，0，1)则相反;在耦合最强的声腔深度处，腔控模态(0，0，1)和板控模态(3，1)的衰减时间趋于相等.

图5(c)中，随着声腔深度增加，腔控模态(0，0，1)和板控模态(3，1)的共振频率变化有3 个特点:①共振频率随声腔深度变化的曲线相交于一点，在相交点处耦合最强;并且离耦合最强点越远，其偏离耦合前的固有频率越小.②腔控模态(0，0，1)的共振频率由高于耦合前的共振频率变成低于耦合前的，出现了跃变现象，而板控模态(3，1)的共振频率则相反.③腔控模态(0，0，1)的共振频率变成了板控模态(3，1)共振频率的延续，而板控模态(3，1)的共振频率是腔控模态(0，0，1)共振频率的延续.

图5 声腔深度对板与声腔耦合的影响(TaN =15 s，TpM =0.5 s)

当声腔深度为0.990 4 m 时，耦合系统中板和声腔2 部分的响应如图6和图7所示，板的振型和耦合前(3，1)模态振型一样，声腔模态(0，0，1)的模态幅值远大于其他阶声腔模态.验证了分析的耦合系统分别是腔控模态(0，0，1)和板控模态(3，1).

图6 板振动速度分布(TaN =15 s，TpM =0.5 s)

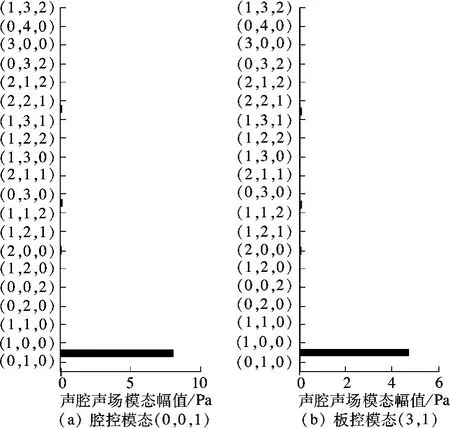
图7 声腔声场模态幅值(TaN =15 s，TpM =0.5 s)

4 结论

1)模态耦合系数决定板模态和声腔模态是否耦合.当模态耦合系数不为零时，模态之间有可能耦合;反之，则一定不耦合.而传递因子决定板和声腔的模态耦合程度，传递因子越大耦合越强，板和声腔的模态之间能量传递也越大.

2)声腔深度Lz对传递因子的影响分为2 种:①当声腔模态序数n=0 时，声腔深度直接决定传递因子大小;②当声腔模态序数n≠0 时，传递因子由对应耦合前共振频率差决定.

3)调整声腔深度使声腔和板的模态间传递因子越大，则它们之间的耦合越强，耦合后的系统共振频率、模态衰减时间较耦合前偏离越大.

References)

［1］Fahy F J，Gardonio P.Sound and structural vibration radiation，transmission and response［M］.London:Academic Press，2007:418-427.

［2］姚昊萍，张建润，陈南，等.不同边界条件下的封闭矩形声腔的结构-声耦合分析［J］.声学学报，2007，32(6):497-502.

Yao Haoping，Zhang Jianrun，Chen Nan，et al.Analysis of structural-acoustic coupling of elastic rectangular enclosure with arbitrary boundary conditions［J］.Acta Acustica，2007，32(6):497-502.(in Chinese)

［3］姚昊萍，张建润，陈南，等.弹性长方体封闭结构腔声辐射建模与分析［J］.东南大学学报:自然科学版，2005，35(6):889-893.

Yao Haoping，Zhang Jianrun，Chen Nan，et al.Modeling and analysis of sound radiation of elastic rectangular enclosure［J］.Journal of Southeast University:Natural Science Edition，2005，35(6):889-893.(in Chinese)

［4］罗超，饶柱石，赵玫.基于格林函数法的封闭声腔的结构-声耦合分析［J］.振动工程学报，2004，17(3):296-300.

Luo Chao，Rao Zhushi，Zhao Mei.Analysis of structural-acoustic coupling of an enclosure using Green function method［J］.Journal of Vibration Engineering，2004，17(3):296-300.(in Chinese)

［5］Pan J，Bies D A.The effect of fluid-structural coupling on sound waves in an enclosure—theoretical part［J］.Journal of the Acoustical Society of America，1990，87(2):691-707.

［6］Kim S-M，Brennan M J.A compact matrix formulation using the impedance and mobility approach for the analysis of structural-acoustic system［J］.Journal of Sound and Vibration，1999，223(1):97-113.

［7］靳国永，杨铁军，刘志刚，等.弹性板结构封闭声腔的结构-声耦合特性分析［J］.声学学报，2007，32(2):178-188.

Jin Guoyong，Yang Tiejun，Liu Zhigang，et al.Analysis of structural-acoustic coupling of an enclosure surrounded by flexible panel［J］.Acta Acustica，2007，32(2):178-188.(in Chinese)

［8］Pan J，Hansen C H，Bies D A.Active control of noise transmission through a panel into a cavity:Ⅰ.analytical study［J］.Journal of the Acoustical Society of America，1990，87(5):2098-2108.

［9］Pan J，Hansen C H.Active control of noise transmission through a panel into a cavity.Ⅲ:effect of the actuator location［J］.Journal of the Acoustical Society of America，1991，90(3):1493-1501.

［10］Kim S M，Brennan M J.Active control of harmonic sound transmission into an acoustic enclosure using both structural and acoustic actuators［J］.Journal of the Acoustical Society of America，1999，107(5):2523-2534.

［11］Jin Guoyong，Liu Zhigang，Yang Tiejun.Active control of sound transmission into an acoustic cavity surrounded by more one flexible plate［J］.Noise Control Engineering Journal，2009，57(3):210-220.