一种基于压缩感知的无损图像认证算法

艾 鸽 伍家松，2 段宇平，2 舒华忠，2

(1 东南大学影像科学与技术实验室，南京210096)

(2 中法生物医学信息研究中心，南京210096)

随着网络技术的迅速发展，信息交流和共享变得越来越容易，在这个过程中，信息的完整性和可靠性受到越来越严重的威胁.计算机软件功能的日益强大，使得多媒体数据的篡改更容易被普通人所掌握.诸如“正龙拍虎”、“藏羚羊穿越青藏铁路”等被广泛报道的虚假新闻图片造成了恶劣的社会影响.因此，对信息进行安全认证十分必要.多媒体数据认证的目的是确认数据是否完整、真实，是否经过任何处理过程，并对其来源进行判定.多媒体数据认证在电子商务和政务、法庭证据、新闻传媒、金融、保险、公安和医疗等领域均有着广泛的应用.

无损图像认证要求提取水印信息后，能恢复原始图像，确保经过认证的图像完全真实可信.无损图像认证在特殊领域(如医学、军事等)的应用使得越来越多的研究者开始关注这项技术.文献［1］提出了一种图像自嵌入与自恢复的水印算法，不仅能检测和定位恶意篡改，而且能恢复被损坏的图像内容;但该算法并非完全可逆，不能完全恢复原始图像.文献［2］提出了一种基于水印的可逆图像认证方案，能够检测篡改且可以实现篡改定位;但该算法将认证水印直接嵌入到像素最不重要位，鲁棒性较差.文献［3］提出了一种基于分块的可逆认证算法，将图像分为可逆块与不可逆块，不可逆块用来提取图像特征，可逆块则利用差值扩展算法嵌入自身块的特征和其他分块的特征信息，该算法不仅能精确恢复原始图像，还能够对恶意篡改攻击进行精确定位;但算法较复杂，且要求可逆块数目不少于非可逆块的数目，否则可逆认证不能实现.文献［4］利用插值扩展和纠错编码，实现了一种能够定位篡改图像块的可逆图像认证方案;但纠错编码并不能完全保证水印提取的正确性.文献［5］将图像分块后进行压缩传感随机投影，并将投影值作为零水印注册保存，不仅不改变图像像素值，而且能够检测定位篡改;但由于注册所需的零水印数据库容量有限，该算法具有一定的局限性.

本文提出的水印算法属于完全认证.首先，对原始图像进行压缩感知随机投影，得到测量值.然后，利用基于哈希的消息认证码(HMAC)生成水印信息，并通过量化索引调制(QIM)算法将其嵌入到图像小波变换后的低高频系数中.最后，利用整数小波逆变换得到含水印图像.量化索引调制过程是不可逆的，恢复时需要额外的误差信息，因此将量化索引调制产生的误差信息作为恢复密钥保存.

1 水印生成

1.1 压缩感知

压缩感知理论由Candès 等［6－7］提出.只要信号在某个正交空间是可压缩的或具有稀疏性的，就能以较低的频率采样信号，并通过非线性的优化算法从采样信号中高概率重构出原信号.但一般的自然信号并不是绝对稀疏的，需要在某种稀疏基上进行稀疏表示.

假设一个长度为N 的实值时间离散信号x，经过一个大小为M ×N 测量矩阵线性投影，得到长度为M(M≪N)的测量值y，即

式中，Φ 为测量矩阵，其大小为M ×N.若信号s 在Ψ 上是稀疏的，则式(1)可描述为

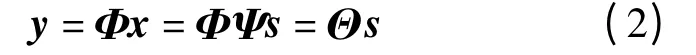
式中，Ψ 为稀疏矩阵;Θ=ΦΨ，其大小为M ×N.

当矩阵Θ 满足有限等距性质准则［8－9］时，压缩感知理论能够通过求解式(2)的逆问题，得到稀疏系数s，然后通过公式x=Ψs 得到x.

Candès 等［6－7］证明，压缩感知信号重构问题可由l0－范数最小值求解式(2)得到s 的估计，数学模型为

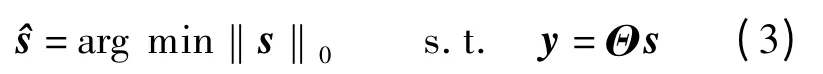
但是对l0－范数的求解是一个NP 问题，即难以求解或者无法验证解的可靠性，因此需要寻求一种更有效的等价求解方法.l1－范数最小问题在一定条件下和l0－范数最小化问题具有等价性，可以得到相同的解.因此，式(3)可以转化为l1－范数最优化问题，即

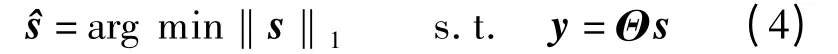
式(4)为凸优化问题，可转化为线性规划求解.

1.2 水印生成步骤

压缩感知测量值作为图像的内容特征，不仅完整表征了图像，且数据量远小于原图像.而观测矩阵元素可对图像间的细微差别进行加权累加使之放大，继而保证相近图像不会生成相似的观测值.另外，测量矩阵所具有的加密作用保证了攻击者在不知道密钥的情况下无法通过测量值恢复原始图像的内容，满足了水印的保密要求［10］.与其他自嵌入水印算法相比，基于压缩感知的水印对原始图像的信息提取更加全面，安全性更好［5］.

水印生成具体步骤如下:

1)将图像分成若干块，分块大小可以根据水印数据量和定位精度调整.

2)对各个图像块进行分块压缩感知.

3)将各块压缩感知随机投影得到的压缩测量值作为HMAC 的输入，得到消息认证码.HMAC需要1 个加密哈希函数H(MD5 或SHA－1)和1 个密钥，可以理解为在原有的哈希函数中添加了密钥，故其安全性不完全依赖于所采用的哈希函数.HMAC 的计算公式为［11］

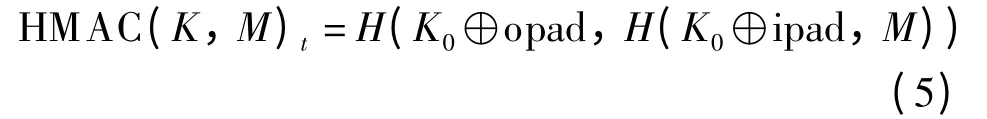
式中，K 为认证密码;K0为密钥，其长度为B;t 为认证码的长度，MD5 中t =16，SHA－1 中t =20;opad 为由B 个字节0x5a 组成的字符串;ipad 为由B 个字节0x36 组成的字符串;M 为待加密的输入数据.其具体流程为

①在K 后添0 创建字长为B 的字符串K0;

②将K0和ipad 进行异或运算;

③将M 添至步骤②生成的字符串上;

④将H 作用于步骤③生成的数据流上;

⑤将K0和opad 进行异或运算;

⑥将步骤④的结果填充至步骤⑤生成的数据流中;

⑦将H 作用于步骤⑥生成的数据流，输出最终结果.

本文将SHA－1 作为加密函数，每一分块得到160 bit 的数据，选取其中32 bit 作为该数据块的摘要信息.所有分块比特流记作S，即认证水印为S.

2 水印嵌入

2.1 量化索引调制算法

为了保证正确定位篡改，必须提取出正确的水印信息，否则未经过篡改区域也会被认为已经篡改，即水印算法具有一定的鲁棒性.目前，常用的鲁棒水印算法是量化索引调制算法.

若图像系数值为f，待嵌入水印数据为wu，则嵌入算法步骤如下［12］:

①计算量化步长个数m(m≥0)以及f 到第m个量化步长的距离r(r ∈［0，2bΔ)，Δ 为量化步长)，即

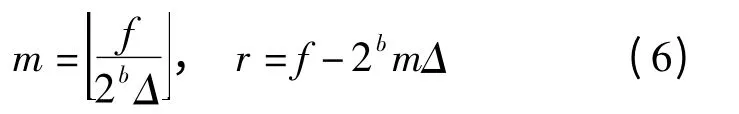
②嵌入水印信息，嵌入后系数值为

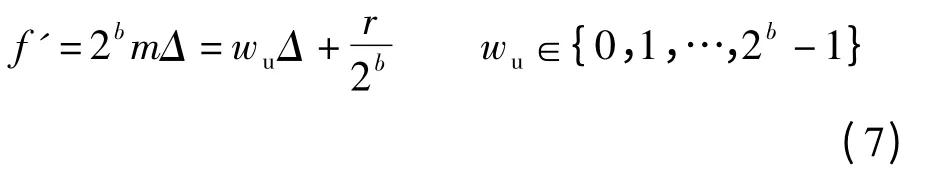
相应的水印提取和图像恢复算法步骤如下:

①计算量化步长个数m′和量化间隔r′，即

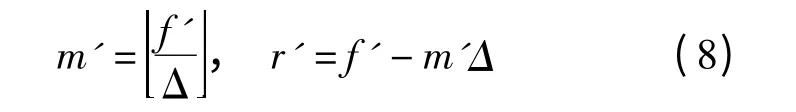
②提取水印数据wu，即

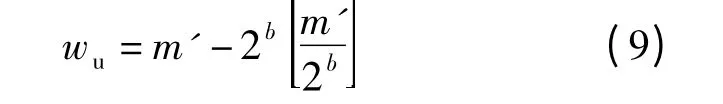
③恢复原始系数f，即

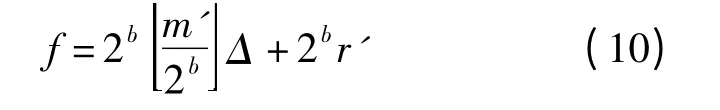
由式(6)和(7)可知，若系数f 的存储精度为n位，则f′的存储精度为n+b 位.精度的不一致导致QIM 算法不可逆，因此需要对f′精度进行修改，即

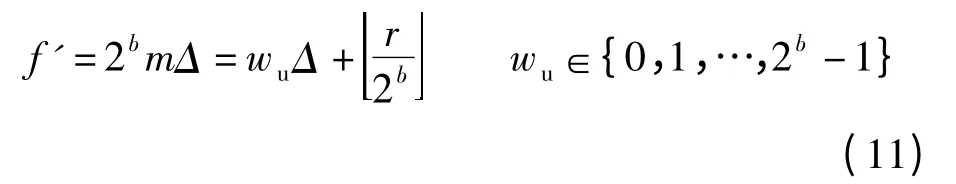
要想无损地恢复原始图像，需要额外存储f′的精度信息.水印提取时，在原有系数的基础上加上额外的精度信息作为f′，利用式(8)～(10)即可无损恢复图像.

2.2 水印嵌入步骤

本文实验中水印嵌入步骤如下:

①为防止嵌入水印后逆运算时溢出，需要对图像进行预处理.若图像像素值为p(p∈［0，2b－1］)，则预处理公式为

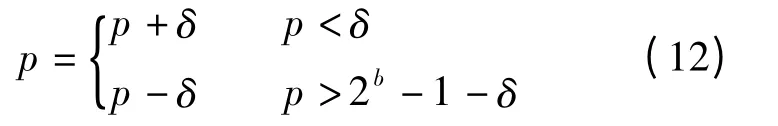
式中，δ 为预处理阈值，可根据图像亮度进行调整.为了在水印提取端恢复原始图像，需要存储预处理信息.假设生成一个位置图Lm，大小与图像相同.若像素值利用式(12)移位，则该位置图处标为1;否则，标为0.然后，将位置图信息压缩，压缩后的位置图记作Lf，则所有待嵌入水印信息为D =S∪Lf=b1b2…bm，其中b1，b2，…，bm∈{0，1}.

②对图像进行整数小波变换，得到低高频子带系数值C.

③保存C 的奇偶信息，生成位置图Lp.此奇偶信息即作为量化索引调制逆变换时的精度信息.保存该位置图Lp，作为图像恢复密钥.

④利用式(6)～(11)，将水印信息D 嵌入到系数C 中.此处，式(6)～(11)中b =1，即水印信息是二值的.

⑤经过小波逆变换即可得到加水印图像.

3 水印提取与篡改检测

水印提取是水印嵌入的逆过程，步骤如下:

①对图像进行整数小波变换，得到低高频小波系数值.

②利用图像恢复密钥Lp及QIM 逆算法提取出水印信息D 并恢复系数C，然后进行小波逆变换.

③若图像分块总数为T，则认证水印为D 中前32T 个信息流.S 以后的信息流设为D1.

④根据D1以及EOS 标志得到预处理位置图信息流Lf，解码后得到Lm.

⑤利用Lm恢复图像.

⑥将恢复后的图像按相同的生成算法得到比特流R，然后将R 划分为多个等长的比特流rl(l =0，1，…，T)，每个等长比特流为32 bit.同时对S 进行同样的操作，得到sl(l=0，1，…，T).分别将其进行比较，若相等，则认为相应的图像块是可认证的;否则，认为该算法已被篡改.

4 实验结果与分析

下面从不可感知性和篡改认证性来分析本文算法的性能.实验环境为Windows XP，Matlab 2010b，位置图压缩采用游程编码和哈夫曼编码.

4.1 不可感知性

水印的不可感知性一般使用峰值信噪比(PSNR)来衡量，其计算公式为

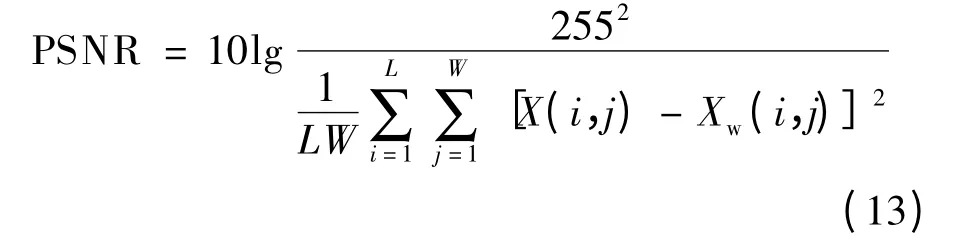
式中，X(i，j)，Xw(i，j)分别为嵌入水印前、后的像素值;L，W 分别为图像的长和宽.PSNR 值越大，表明水印的不可感知性越好.

选择如图1所示的图像进行实验，并与文献［3－4］的算法进行比较，结果见表1.由表可知，本文算法对不同纹理的图像均具有较好的不可感知性，满足视觉上不可觉察的要求.

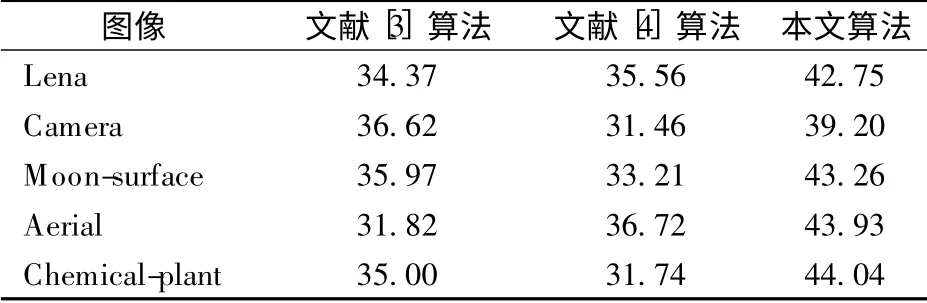
表1 PSNR 比较

4.2 篡改认证性

图1 测试图像

将压缩感知随机投影测量值作为图像内容特征，不仅能较好地表征图像，减小数据量，而且对篡改具有强敏感性.压缩传感测量值之所以能检测篡改是因为具有差异放大的功能，即图像间的细微差别都会被放大.这个差异放大的能力实际是通过测量矩阵对差异进行加权累加实现的［5］.即使是差异很小的测量值，通过哈希函数后也会有很大的差异.因而即使图像只有1 bit 的改变也会被检测出来.

对Lena，Fruits，Truck 图像加水印后，分别进行伪版权标记、复制－篡改伪造以及图像修复攻击，利用本文算法进行篡改检测与定位，结果见图2～图4.

图2 Lena 认证

图3 Fruits 认证

图4 Truck 认证

由图2～图4可知，本文算法对这种局部篡改具有较好的认证效果.目前，图像认证算法多采用鲁棒性(即抗攻击能力)来比较其篡改认证性能，且大多针对有损图像认证算法，无损图像认证算法很大程度上属于完全脆弱水印，鲁棒性相对较弱，不具有可比较性，故此处未与其他算法进行比较.

5 结语

本文提出了一种基于压缩感知的无损图像认证算法.该算法首先对图像进行压缩感知随机投影，将得到的测量值作为HMAC 输入值，生成图像的摘要.然后，利用量化索引调制算法，将生成的水印信息嵌入到图像小波域中.实验结果表明，该算法具有较好的不可感知性，且能够对图像进行认证，定位篡改区域.若图像经过认证，则可无损恢复原始图像.由此可见，该算法可应用于医学图像处理.可将医学图像分为ROI 区域和RONI 区域，将病患信息和ROI 认证信息嵌入到RONI 区域，不仅可对ROI 区域进行认证，还保证了水印的鲁棒性以及可逆性.本文算法的不足之处在于，水印生成的严谨性使得提取端无法区分恶意篡改与无意篡改，这需要在后续工作中进一步改进.

References)

［1］张鸿宾，杨成.图像的自嵌入及窜改的检测和恢复算法［J］.电子学报，2004，32(2):196－199.Zhang Hongbin，Yang Cheng.Temper detection and self recovery of images using self－embedding［J］.Acta Electronica Sinica，2004，32(2):196－199.(in Chinese)

［2］Gao T，Gu Q.Reversible image authentication based on combination of reversible and LSB algorithm ［C］//Proceedings of 2007 International Conference on Computational Intelligence and Security Workshops.Harbin，China，2007:636－639.

［3］Gu Q，Gao T.A new image authentication based on reversible watermarking algorithm［C］//Proceedings of the 7th World Congress on Intelligent Control and Automation.Chongqing，China，2008:2727－2731.

［4］文家福，王嘉祯，刘爱珍，等.基于差值扩展和纠错编码的可逆图像认证［J］.计算机工程，2009，35(22):125－127.

Wen Jiafu，Wang Jiazhen，Liu Aizhen，et al.Reversible image authentication based on difference expansion and error correction code［J］.Computer Engineering，2009，35(22):125－127.(in Chinese)

［5］赵春晖，刘巍.基于分块压缩感知的图像半脆弱零水印算法［J］.自动化学报，2012，38(4):609－617.

Zhao Chunhui，Liu Wei.Block compressive sensing based image semi－fragile zero－watermarking algorithm［J］.Acta Automatica Sinica，2012，38(4):609－617.(in Chinese)

［6］Candès E，Romberg J，Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52(2):489－509.

［7］Donoho D.Compressed sensing ［J］.IEEE Transactions on Information Theory，2006，52(4):1289－1306.

［8］Candès E，Romberg J.The restricted isometry property and its implications for compressed sensing ［J］.Comptes Rendus Mathematique，2008，346(9):589－592.

［9］Baraniuk R，Davenport M，Devore R，et al.A simple proof of the restricted isometry property for random matrices［J］.Constructive Approximation，2008，28(3):253－263.

［10］Rachlin Y，Baron D.The secrecy of compressed sensing measurements［C］//Proceedings of the 46th Annual Allerton Conference on Communication，Control and Computing.Urbana－Champaign，IL，USA，2008:813－817.

［11］周燕，张德丰，马子龙.基于压缩传感的图像哈希水印算法研究［J］.中山大学学报:自然科学版，2010，49(6):58－63.

Zhou Yan，Zhang Defeng，Ma Zilong.The research of image hash watermarking algorithm based on compressed sensing［J］.Acta Scientiarum Naturalium Universitatis Sunyatseni，2010，49(6):58－63.(in Chinese)

［12］Peng F，Lei Y，Li C，et al.A reversible watermarking scheme for 2D engineering graphics based on improved quantization index modulation［C］//Proceedings of the 3rd International Conference on Crime Detection and Prevention.London，UK，2009:1－6.