三次Bézier曲线与圆弧有重合点时的Hausdorff距离

张松枝， 王旭辉， 唐 烁

（合肥工业大学数学学院，安徽 合肥 230009）

三次Bézier曲线与圆弧有重合点时的Hausdorff距离

张松枝， 王旭辉*， 唐 烁

（合肥工业大学数学学院，安徽 合肥 230009）

Hausdorff距离常用来度量两条曲线的匹配程度，因此，它可以用来度量三次Bézier曲线与圆弧之间的逼近程度。论文给出了三次Bézier曲线与圆弧在中点重合时，它们之间的Hausdorff距离表达式；以及三次Bézier曲线与圆弧在一般情况重合（除端点外）时的 Hausdorff距离表达式。通过这些表达式可以直接得出三次 Bézier曲线与圆弧之间的Hausdorff距离。

Hausdorff距离；圆弧；Bézier曲线

Hausdorff距离是用来度量两个集合之间的最大不匹配程度，因此，Hausdorff距离经常用在CAD/CAM 系统或是作为逼近理论，是非常重要的理论知识[1-3]。圆弧曲线是几何造型中一种相当基本的曲线类型，而基于多项式的CAD/CAM 造型系统并不能精确表示圆弧。由于目前通用的CAD/CAM 系统都包含了Bézier曲线，所以为了在不同的CAD/CAM系统之间传递数据，更好地应用圆弧，人们常使用Bézier曲线逼近圆弧。在过去的 30多年里，已经做出了大量的工作，例如Dokken，Ahn与Kim，Floater均对Bézier曲线逼近圆弧进行了研究[1-10]。但是，对于一般曲线之间的 Hausdorff距离较难求得，本文主要给出了当三次 Bézier曲线与圆弧有重合点时其Hausdorff距离的显式结果。从而可以清楚的知道三次 Bézier曲线对圆弧的逼近程度，即通过Hausdorff距离误差来讨论三次Bézier曲线与圆弧的逼近程度。

1 中点重合时Hausdorff距离

1.1 相关定义

首先给出两条曲线段之间的 Hausdorff距离的定义。给定两条曲线段

P (t)与 Q (s)之间的Hausdorff距离定义如下：

圆弧是几何造型中一类常用的曲线类型。对于一般的圆，人们可以通过坐标平移、旋转以及均匀放缩把其变为一个圆心在坐标原点的单位圆。在本文中，只考虑圆心在原点的单位圆上的圆弧曲线，而且假设圆弧的一个端点坐标为(1,0)。设圆心位于原点的单位圆弧的参数表示如下：

相对于二次Bézier曲线，三次Bézier曲线具有更高的逼近精度。本文主要讨论如何用三次Bézier曲线来逼近圆弧.为了更好的逼近圆弧，可给出下面基本要求：

1） Bézier曲线与圆弧有相同的起点和终点

2） Bézier曲线与圆弧在起点与终点处有相同的切向量，即

由于圆弧自身具有轴对称性的性质，那么就希望所构造的三次Bézier曲线也具有轴对称性。因此可设三次Bézier曲线的控制顶点如下：

1.2 中点重合时Hausdorff距离显式表达式

由文献[11-13]可知，对于任意两条不同的曲线 P (t)与 Q (s)之间的Hausdorff距离，其满足下列关系：

其中， P '(t)，Q '(s)分别为 P (t)关于变元t求导与 Q (s)关于变元s求导的求导。

易知给定圆弧式（1）上的(c os(θ) ,sin(θ))⊥(c os'(θ) ,sin'(θ) )，所以只需求t使其满足关系式(x ( t),y( t) )⊥ (x '( t),y'( t) )即可。因此，可将求圆弧与三次Bézier曲线之间的Hausdorff距离转换为求解方程

设t1,… ,tn为方程式（4）的解，则圆弧与Bézier曲线的Hausdorff距离为

以下将研究给定圆弧式（1）与给定三次Bézier曲线式（3）有中点重合时，其Hausdorff距离的距离表达式。

定理 1 给定圆弧式（1）及其对应的三次Bézier曲线式（3）。当圆弧与三次Bézier曲线在中点重合时，圆弧与三次 Bézier曲线之间的Hausdorff距离为

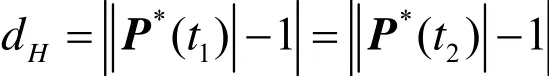
证明 三次 Bézier曲线式（3）的中点为P*(1/2) =(x(1/2),y (1/2))，由于其在圆弧上，可得 x( 1/2)2+ y(1/2)2=1，

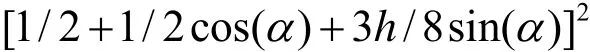
即

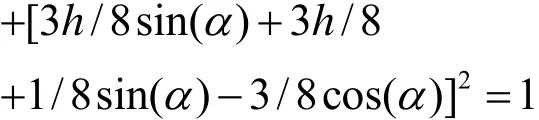
求解可得

将

代入式（4），可得方程式（4）的根为：

由于

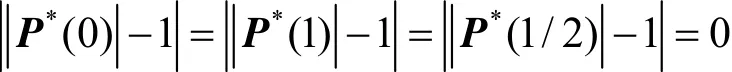
所以

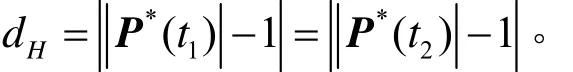
1.3 一般点重合时的Hausdorff距离显式表达式

以上文章给出的是当圆弧式（1）与三次Bézier曲线式（3）在中点重合时的Hausdorff距离，那么当圆弧式（1）与三次Bézier曲线式（3）在一般点重合时的Hausdorff距离又该如何计算。通过分析研究可得下述定理：

定理 2 给定圆弧式（1）及其对应的三次Bézier曲线式（3）。当圆弧式（1）与三次Bézier式（3）曲线在参数 t0,t0∈ (0,1)处重合时：

1） 当 t0∈ (δ,1 - δ)时，圆弧式（1）与其对应的三次Bézier曲线之间的Hausdorff距离为

2） 当 t0∈ (0,δ)或 t0∈ (1 - δ,1)时，圆弧式（1）与其对应三次Bézier曲线之间的Hausdorff距离为

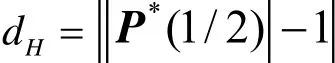
证明 假设三次 Bézier曲线在 t =t0, t0∈ (0,1)处与圆弧在(c os(β) ,sin(β) )点重合，可得

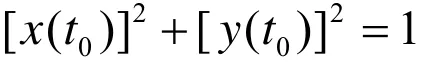
即

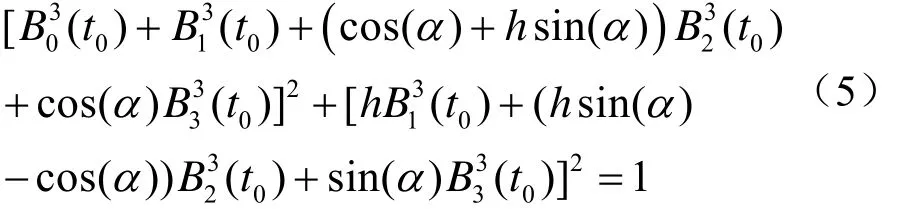
求解方程（5）可得h的值为

其中

根据假设我们取h为正值h2，将h2代入三次∑3x( t) Bézier曲线P*(t) =p B3(t )，求解方程

ii i=0 x'( t) + y( t) y'( t )=0，可得

易知t1,t2, t3, t4, t5与α大小无关，且

我们令

通过计算可得，当t0∈ (δ,1-δ)时，

当t0∈ (0,δ)或 t0∈ (1 - δ,1)时，。证毕。

由以上内容可知，圆弧式（1）与其对应三次 Bézier曲线式（3）在 t0重合时的 Hausdorff距离与它们在1-t0重合时的Hausdorff距离相等，即满足了图像的对称性。

2 应用实例

下面给出上述定理的应用实例

例 1 给定圆弧角度 α=π/3,π/2,2π/3π时，与其对应三次Bézier曲线式（3）在 t=1/2处重合，则可得到下列误差图形

例2 给定圆弧式（1）角度α =π/6,π/3, π/2,2π/3,3π/4,π时，与其对应三次Bézier曲线式（3）在参数 t0=1/3处重合时，则可得到下列误差图形

图2 Hausdorff距离都在 1/2t=处取得

例3 给定圆弧式（1）角度α =π/3,π/2, 2π/3时，与其对应三次Bézier曲线式（3）在参数 t0=3/5处重合时，则可得到下列误差图形

图3 Hausdorff距离都在t =(3 - 33 - 8 t0+ 8t 02)/6=1/5处取得

3 总 结

本文给出了圆弧式（1）的三次Bézier曲线，式（3）与圆弧式（1）在中点重合时，它们之间Hausdorff距离显式表达式以及在一般情况下，t=t0(0 ＜ t0＜ 1)有重合点时，它们之间的Hausdorff距离显式表达式。我们通过这些Hausdorff距离显示表达式直接得出圆弧式（1）与三次Bézier曲线式（3）之间的Hausdorff距离。

[1] Kim S H, Ahn Y J. An approximation of circular arcs by quatic Bézier curves [J]. Computer Aided Geometric Design, 2007, 39:490-493.

[2] Ahn Y J. Conic approximation of planar curves [J]. Computer Aided Geometric Design 2001, 33(12):867-872.

[3] Farouki R T, Neff C A. Analytic properties of plane offset curves [J]. Computer Aided Geometric Design 1990, (7):83-99.

[4] Ahn Y J, Kim H O. Approximation of circular arcs by Bézier curves [J]. Journal of Computational and Applied Mathematics, 1997, 81(1):145-163.

[5] Ahn Y J. Helix approximations with conic and quadratic Bézier curves [J]. Computer Aided Geometric Design, 2005, 22:551- 565.

[6] Blinn J. How many ways can you draw a circle [J]. IEEE Computer Graphics Application, 1987, 7(8):39-44.

[7] Dokken T, Dachlen M, Lyche T, et al. Good approximation of circle by curvature-continuous Bézier curves [J]. Computer Aided Geometric Design, 1990, (7):33-41.

[8] Goldapp M. Approximation of circular arcs by cubic polynomials [J]. Computer Aided Geometric Design 1991, (8):227-238.

[9] 范劲松, 安 军, 徐宗俊．用三次NURBS表示圆弧与整圆的算法研究[J]．计算机辅助设计与图形学学报, 1997, 9(5):391-395.

[10] Ahn Y J, Kim H O, Lee K Y. G1 arc spline approximation of quadratic Bézier curves [J]. Computer Aided Geometric Design, 1998, 30(8):615- 620.

[11] Ahn Y J, Kim Y S, Shin Y S. Approximation of circular arcs and offset curves by Bezier curves of high degree [J]. J. Comp. Appl. Math, 2004, 167:181-191.

[12] Floater M. High-order approximation of conic sections by quadratic splines [J]. Computer Aided Geometric Design, 1995, 12(6):617-637.

[13] Floater M. An o(h2n) Hermite approximation for conic sections [J]. Computer Aided Geometric Design, 1997, 14:135–151.

Hausdorff Distance between Cubic Bézier Curve and Circular Arc with a Coincidence Point

Zhang Songzhi, Wang Xuhui, Tang Shuo
( School of Mathematics, Hefei University of Technology, Hefei Anhui 230009, China )

Hausdorff distance is often used to measure the distance between two curves. It can be used to measure the distance between cubic Bézier curve and circular arc. In the paper, the closed form of the Hausdorff distance between the circular arc and the cubic Bézier curve is given when they have a coincidence point.

Hausdorff distance; Circular arc; Bézier curve

TP 391

A

2095-302X (2013)02-0072-04

2012-06-20；定稿日期：2012-08-29

张松枝（1987-），女，安徽阜阳人，硕士研究生。主要研究方向为数值逼近。Email：253209502@qq.com

王旭辉（1980-），男，安徽巢湖人，博士研究生。主要研究方向为计算机辅助几何设计。Email：xhw@hfut.edu.cn