一种平面点集Voronoi图的细分算法

寿华好， 袁子薇， 缪永伟， 王丽萍

（1. 浙江工业大学理学院，浙江 杭州 310023；2. 浙江工业大学计算机科学与技术学院，浙江 杭州 310023；3. 浙江工业大学经贸管理学院，浙江 杭州 310023）

一种平面点集Voronoi图的细分算法

寿华好1， 袁子薇1， 缪永伟2， 王丽萍3

（1. 浙江工业大学理学院，浙江 杭州 310023；2. 浙江工业大学计算机科学与技术学院，浙江 杭州 310023；3. 浙江工业大学经贸管理学院，浙江 杭州 310023）

Voronoi图是计算几何中的重要概念之一，在计算机图形学、计算几何、计算机辅助几何设计、有限元网格划分、机器人轨迹控制、模式识别、气象学和地质学研究中得到广泛应用。借助于四叉树和区间算术，提出了一种新的构造平面点集Voronoi图的细分算法, 并且和经典的增量算法、栅格扩张法进行了比较, 结果显示新细分算法更为有效。最重要的是细分算法原理简单，很容易编程实现。

Voronoi图；细分算法；增量算法；栅格扩张法；区间算术

Voronoi图的应用领域非常广泛，在Voronoi图明确定义以前，1644年法国数学家 Descartes（笛卡尔）发表的太阳系及其周边天体的发布图，就是一种 Voronoi图，而且还是一种加权Voronoi图[1]。1932年B.N.Delone给出了“Voronoi区域”的概念，标志着Voronoi图作为计算几何的一个研究分支的正式诞生[1]。其后在生物学、化学、流体力学、医学等诸多领域得到广泛应用。作为当前计算几何学科的一个研究热点，就其重要性来说，Voronoi图是仅次于凸壳的一个重要的几何结构[2]。在不同的领域，Voronoi图有时也被称为 Thiessen多边形[1]、Dirichrit网格、或Wigner-Seitz域等[3]。Voronoi图的基本定义和算法可见于许多计算几何教科书。它是关于空间邻近关系一种基础数据结构。Voronoi图有二维和三维、狭义和广义、一阶和高阶之分[2]。其中最基本、应用最广泛和研究最深入的还是二维欧氏空间平面点集 Voronoi图，平面线集和面集Voronoi图可以通过平面点集Voronoi图处理近似获得[4]。平面点集 Voronoi图常用构造算法主要包括矢量方法[3]和栅格方法[5-6]，基于矢量的方法有对偶生成法、增量构造算法、分治法、减量算法、平面扫描算法[3]；基于栅格的方法有邻域栅格扩张法和栅格邻近归属法[5-6]。在矢量方法中，增量构造算法的时间复杂度在最坏的情况下为O(n2)，其中n为平面点集中点的个数，在一般情况下其运行时间为，在改进的 Voronoi图增量构造方法中，时间复杂度为 O( n logn)[7]，分治法、减量算法和平面扫描算法的时间复杂度为O( n log2n)，间接法的时间复杂度取决于其对偶Delaunay三角网获取的时间复杂度[68]。国内外研究者根据其应用对传统的 Voronoi划分或Delaunay三角剖分算法进行了一系列的改进[9-11]。栅格法与矢量法相比,思想较为简单，易于向三维空间扩展，但是它的精度受到栅格单元大小的限制，一般耗时长，精度不高[12-13]，栅格法中相对比较新的方法为一种经过改进的栅格扩张法[13]，其时间复杂度为 O( m2- n2)，其中m为栅格的总数量。我们在本文中提出的平面点集Voronoi图的细分算法是一种全新的栅格法，由于我们在细分算法中使用了四叉树和区间算术，当判断出某一平面区域中没有Voronoi图的时候可以整个地把这个平面区域抛掉，不需要对每一个栅格一个一个地处理，从而极大地提高了栅格法的计算速度，这一点在我们所运行的实例中可以看得很清楚。此外，更重要的是细分算法原理更为简单，非常容易编程实现。细分算法在最坏的情况下的时间复杂度为 O (mn)，实际计算的时候由于细分算法可以成片地抛掉不包含 Voronoi图的平面区域，从而实际计算量远远小于这个数。

在Voronoi图中，被用来划分空间的各个基本图形元素一般被称为站点。最基本的 Voronoi图是以平面点集 p={pi, i =1,2,…,n}为站点的Voronoi图，它将平面划分成凸多边形形状的Voronoi 区域，p中的每个站点 pi，对应一个这样区域 vi，使得 vi内的任何点距离 pi比距离其它站点近。本文的基本思想是在给定的矩形区域中找出所有到站点 pi的最短距离至少在两处或以上达到的像素（也就是栅格）集合，此像素集合即是平面点集p的Voronoi图，在求解过程中借助于四叉树数据结构和区间运算技术进行加速[14]。

1 细分算法

假设 p1( x1, y1)， p2(x2, y2)… pn(xn,yn)是给定的二维平面上的n个点，所考虑的平面矩形区域是，像素点大小（即像素点的长度和宽度中较大的那个）为ε。计算该平面矩形区域内这n个点的Voronoi图，相当于计算该平面矩形区域内到这些点的最短距离至少有两处或两处以上达到的像素点全体。

根据以上细分算法的基本原理, 我们给出细分算法的具体步骤如下：

1） 输入n个平面点 p1( x1, y1)，p2( x2, y2)… pn( xn, yn)以及所在的平面矩形区域和像素的大小ε。

3） 画出 p1( x1, y1)， p2(x2,y2)… pn(xn,yn)以及Voronoi图M，算法结束。

以上细分算法充分利用了Voronoi区域的连贯性，当算法判断出某矩形区域内不可能包含Voronoi图的时候，可以把整个矩形区域丢掉，从而运行效率比较高。

由于到目前为止，虽然构造平面点集Voronoi图的算法有很多，但是经典的增量算法是最常用的构造Voronoi图的方法[7]。栅格法也出现了很多新的算法，本文对比的就是一种新的栅格扩张方法。我们考虑将这里新提出的细分算法与增量算法、栅格扩张法作一个比较，以便通过比较看一看细分算法的表现如何。 经典增量算法的基本思想是：在已构造的输入了站点的Voronoi图的基础上, 逐步加入新的站点, 再利用局部特性, 通过局部修改已有的Voronoi图来生成新的Voronoi图，即对于平面离散的站点集合{p1,p2,… ,pn}，在站点集合{p1,p2,… ,pi}(i ＜ n)的 Voronoi图的基础上, 再加入新的站点 pi+1, 然后通过局部修改来构造{p1,p2,… ,pi,pi+1}的Voronoi图。如此不断加入新的站点, 最后即可得到点集{p1,p2,…,pn}的Voronoi图[7]。增量算法的具体步骤如下[2]：

1） 产生 p1, p2，做的中垂线，输出Voronoi图为中垂线。

2） 产生 p3，连接 p1, p2,p3成三角形，做三边的中垂线，交点为Voronoi点，从该点引出的三条中垂线构成Voronoi图。

3） 产生 pi，判断 pi落入那个Voronoi多边形域内，修改该Voronoi多边形及相应Voronoi多边形的边与顶点。

4） 直至产生点的工作终止[2]。

其中第 3）步，判断 pi落入那个 Voronoi多边形域内比较耗费时间。

栅格扩张法的基本思想是：在平面的栅格空间中，两个栅格 p1( x1, y1)和 p2(x2, y2)间的欧氏距离定义为d(p1.p2)=，计算每一个栅格与其临近的几个发生元栅格之间的欧氏距离，以距离最近的发生元栅格代码作为该栅格的隶属代码，直至定义区域中所有栅格单元的归属都被检索完为止，栅格扩张法的具体步骤如下[15]：

1） 构建栅格。

2） 生成点集{p1, p2,… ,pn}。

3） 查找每个发生元的临近发生元栅格，即每个点的临近发生元栅格。

4） 计算某个栅格与其临近的发生元栅格之间的欧氏距离，以距离最近的发生元栅格的代码作为该栅格的隶属代码。

5） 合并集合。

6） 作图[15]。

其中第4）步计算距离耗时巨大。其计算机时随着栅格变小而增加, 但随着发生元所占栅格数量的增加而减小。

2 细分算法的计算复杂度分析

假设所考虑的平面区域中总的栅格数量为m=k2，而 k=2l，假设平面区域中站点的个数为n。那么在最坏的情况下，也就是说在细分算法的执行过程中一个区域都抛不掉的情况下，总的计算复杂度为 n +4 n +42n +… +4ln =

l+1n=O( 22ln)=O (k2n)=O (mn)，实际计算的时候由于细分算法可以成片地抛掉不包含Voronoi图的平面区域，从而实际计算量远远小于这个数。从这个结果可以看出，细分算法的计算复杂度不但跟站点的个数n有关，而且跟栅格的总数量m也有关。注意到增量算法的时间复杂度在最坏的情况下为 O( n2)，也就是说增量算法的时间复杂度只跟站点的个数n有关，跟栅格的总数量m无关。那么在栅格的总数量m固定的情况下，随着站点个数n的增加，细分算法的计算时间只是线性地增长，而增量算法的计算时间是以平方的速度增长。从这里就可以看出细分算法的优势所在。由于栅格扩张法的时间复杂度为O( m2- n2)，而站点数 n一般远远小于栅格总数m，所以细分算法的计算速度显然比栅格扩张法要快，这一点在以下的实例中也可以看得很清楚。

3 实 例

我们用Mathematica8.0编程实现了上面提出的细分算法，经典的增量算法和栅格扩张法，并在中央处理器为 Intel(R) Core(TM) CPU i5-2410M @ 2.30 GHz的微机系统里运行程序进行了一些实例的计算和比较，下面给出几个例子。

例1 输入两点 p1(0.24, 0.36), p2(0.52, 0.83),图1为细分算法的结果，图2为增量算法的结果，图3为栅格扩张法的结果。

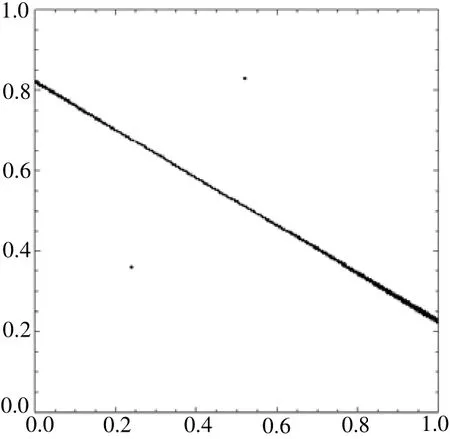
图1 2个点的Voronoi图（细分算法）CPU Time Used:0.156 Second

图2 2个点的Voronoi图（增量算法）CPU Time Used:0.374 Second

图3 2个点的Voronoi图（栅格扩张法）CPU Time Used:105281 Second

图4 5个点的Voronoi图（细分算法）CPU Time Used:1.279 Second

例2 输入5点：p1={0 .35,0}, p2={0.25, 0.45}, p3={0 .5,1},p4={0 .75,0.5},p5={0 .85,0.1},图4为细分算法的结果，图5为增量算法的结果，图6为栅格扩张法的结果。

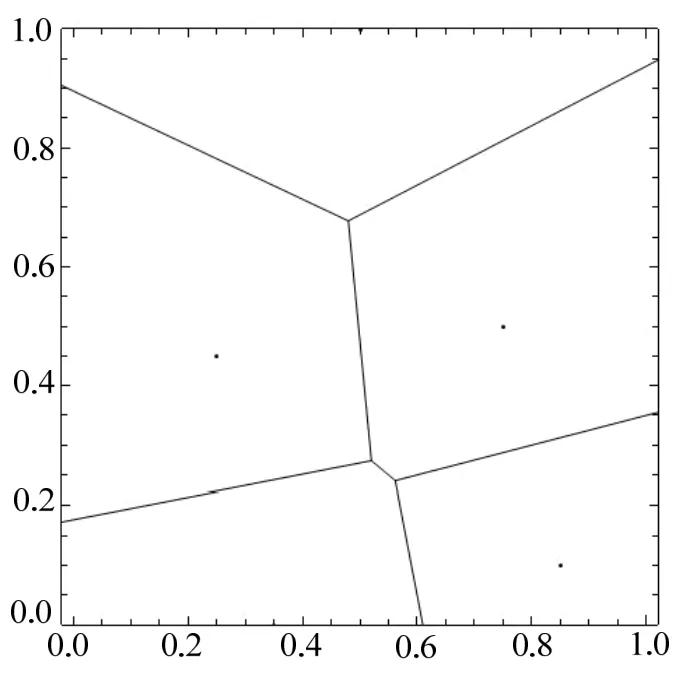
图5 5个点的Voronoi图（增量算法）CPU Time Used:1.423 Second

图6 5个点的Voronoi图（栅格扩张法）CPU Time Used:104441 Second

图8 10个点的Voronoi图（增量算法）CPU Time Used:6.115 Second

例3 输入10点：p1={0 .35,0},p2={0 .25,0.45}, p3={0.5,1},p4={0 .75,0.5},p5={0 .85,0.1}, p6={0 .15,0.3}, p7={0 .95,0.65},p8={0.4,0.2}, p9={0.6,0.7},p10={1 ,0.8},图 7为增量算法的结果，图8为细分算法的结果，图9为栅格扩张法的结果。

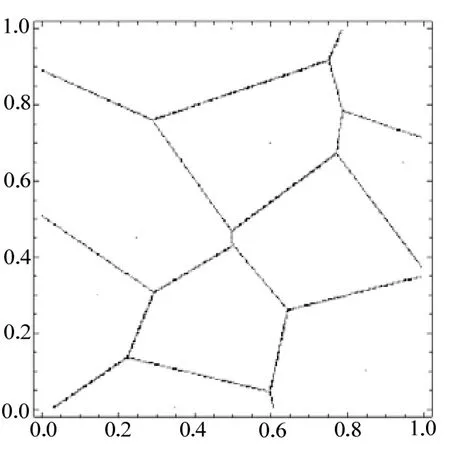
图9 10个点的Voronoi图（栅格扩张法）CPU Time Used:85742.2 Second

图10 100个点的Voronoi图（细分算法）CPU Time Used:144.394 Second

为了说明细分算法的有效性我们还特别增加了一个多点Voronoi图的例子。

例4 随机产生的100个点，图10为细分算法结果。

4 结 论

从以上实例可以看出，本文提出的细分算法可以有效的计算出平面点集的Voronoi图，并且细分算法的运算速度比栅格扩张法要快很多，比经典的增量算法也要快，从算法复杂度分析可以看出增量算法的计算时间随着点数的增加以平方的速度增加，而细分算法的计算时间只是线性地增加，从而多点的时候细分算法的优势就更明显。最重要的是细分算法思想十分简单，非常容易编程实现，而增量算法和栅格扩张法的原理相对比较复杂，实现起来要麻烦多了。此外需要指出的是细分算法得到的是一个包含Voronoi图的像素点的集合，由于区间算术的保守性，部分邻近Voronoi图但是不应包含于Voronoi图的像素点有可能会因为无法排除而被保留了下来，这使得用细分算法得到的Voronoi图的图像在有些地方比实际要粗一些，如何细化是一个值得进一步研究的问题。

[1] 蔡 强. 限定Voronoi网格剖分的理论及应用研究[M]. 北京:北京邮电大学出版社, 2010:5-6.

[2] 周培德. 计算几何—算法分析与设计[M]. 北京:清华大学出版社, 2000:146-216.

[3] 代晓巍, 李树军, 刘晓红. Voronoi图增点构造算法研究[J]. 测绘工程, 2007, 16(1):19-22.

[4] 普雷帕拉塔 F P, 沙莫斯 M I. 计算几何导论[M].北京:科学出版社, 1990:226-277.

[5] 王新生, 刘纪远, 庄大方, 等. 一种新的构建Voronoi图的栅格方法[J]. 中国矿业大学学报, 2003, 32(3):293-296.

[6] 李成名, 陈 军. Voronoi图生成的栅格算法[J]. 武汉测绘科技大学学报, 1998, 23(3):208-210.

[7] 孟 雷, 张俊伟, 王筱婷, 等. 一种改进的Voronoi图增量构造算法[J]. 中国图像图形学报, 2010, 15(6):978-984.

[8] 赵仁亮. 基于Voronoi图的GIS空间关系计算[M]. 北京:测绘出版社, 2006:44-45.

[9] 程 丹, 杨 钦, 李吉刚. 二维黎曼流形的Voronoi图生成算法[J]. 软件学报, 2009, 20(9):2407-2416.

[10] Evazi M, Mahani H. Generation of Voronoi grid based on vorticity for coarse-scale modeling of flow in heterogeneous formations [J]. Transport in Porous Media, 2010, 83(3):541-572.

[11] Žalik B. An efficient sweep-line Delaunay triangulation algorithm [J]. Computer Aided Design, 2005, 37(10):1027-1038.

[12] Okabe A, Boots B, Sugihara K, et al. Spatial tessellations:concepts and applications of voronoi diagrams (second edition) [M]. New York:JohnWiley & Sons Ltd, 2000:287-290.

[13] Li Cheng ming, Chen Jun. Raster methods of the generation of Voronoi diagrams for spatial entities [J]. International Journal of Geographical Information Seience, 1999, 13:209-225.

[14] Martin R, Shou H, Voiculescu I, et al. Comparison of interval methods for plotting algebraic curves [J]. Computer Aided Geometric Design, 2002, 19(7):553-587.

[15] 王新生, 刘纪远, 庄大方, 等. 一种新的构建Voronoi图的栅格方法[J]. 中国矿业大学学报, 2003, 32(5):293-296.

A Subdivision Algorithm for Voronoi Diagram of Planar Point Set

Shou Huahao1, Yuan Ziwei1, Miao Yongwei2, Wang Liping3
( 1. College of Science, Zhejiang University of Technology, Hangzhou Zhejiang 310023, China; 2. College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou Zhejiang 310023, China; 3. College of Business and Administration, Zhejiang University of Technology, Hangzhou Zhejiang 310023, China )

Voronoi diagram is one of the most important concepts in computational geometry, It is applied widely in computer graphics, computational geometry, computer aided geometric design, finite element grid partition, robot trajectory control, pattern recognition, meteorology and geology. Based on quadtree data structure and interval arithmetic technique, a new subdivision algorithm for Voronoi diagram of a planar point set is proposed. A comparison of this subdivision algorithm with the well known incremental algorithm and grid expansion method is conducted. Test results show that the subdivision algorithm is more efficient. The most important is that the idea of subdivision algorithm is very simple and therefore it is easy to implement.

Voronoi diagram; subdivision algorithm; incremental algorithm; grid expansion method; interval arithmetic

TP 391.72

A

2095-302X (2013)02-0001-06

2012-09-02；定稿日期：2012-01-25

国家自然科学基金资助项目（61272309，61070135）

寿华好（1964-），男，浙江诸暨人，教授，博士，主要研究方向为计算机辅助几何设计与图形学。E-mail：shh@zjut.edu.cn