真空预压下考虑渗透系数变化的吹填土地基固结分析

牛飞，邱长林，闫澍旺，纪玉诚

（天津大学建工学院岩土工程研究所，天津 300072）

0 引言

随着经济、人口的增长，我国的土地资源日益紧缺，在这种形势下，围海造陆便成为获取土地资源的重要手段。围海造陆主要是将淤泥吹填到岸，然后采取相应的工程措施，加固由淤泥组成的吹填土，从而形成一定的硬壳层。吹填土具有强度低、灵敏度高、排水固结时间漫长、沉降大等特点[1]，基于吹填土的这些特点，真空预压法便成为吹填土地基加固的主要方法。

围海造陆所用吹填土一般是用港池和航道的淤泥，经水力吹填形成陆域场地，含水量高达80%以上，新近吹填的场地甚至可以达到200%左右，强度和承载力极低，土体尚未完成自重固结[2]。吹填土在自重及堆载作用下产生很大的固结变形，而且其固结系数也随时间变化，如果仍然采用弹性模量和渗透系数为常数计算土的固结变形，计算结果与实际情况相差较大[3]。在吹填土的固结过程中孔隙比变化很大，有效应力与孔隙比之间有非线性关系，渗透系数与孔隙比之间同样具有非线性关系，如何定义有效应力与孔隙比的关系和渗透系数与孔隙比的关系是吹填土固结计算的关键。现今，真空预压在软基处理方面取得了大量的研究成果。但是，对于高含水率吹填土在真空荷载下的变形特征、有限元计算方法以及孔压变化规律的研究还不够深入。因此研究吹填土在真空荷载作用下的变形规律、孔压变化规律具有重要的理论价值和工程实际意义。

目前，在真空预压有限元计算方面取得了很大发展。闫澍旺、陈环[4]采用弹性本构关系，渗透系数为常数分析真空荷载下土体中心点的沉降。董志良、陈平山等[5]详细分析了渗透系数与固结应力的关系，并采用弹性本构关系，考虑了固结过程中渗透系数随有效应力的变化，分析了前期固结压力为150 kPa的土体在真空荷载作用下的固结规律。余湘娟、吴跃东[6]等采用双屈服面黏弹-黏塑性模型，并考虑施工对土体的影响，忽略渗透系数的变化，对岸坡软基在真空预压下的地表沉降和水平位移进行了计算。彭劼、刘汉龙等[7]采用修正的剑桥模型，并考虑渗透系数随孔隙比的变化，把砂井等效成砂墙，分析了公路软基在真空堆载联合预压法作用下的侧向变形。上述有限元分析的研究对象多是一般性软土，这些软土有一定的初始应力，其初始孔隙比相对较小，在真空荷载作用下土体的孔隙比变化有限，故考虑渗透系数随孔隙比变化的有限元模型会使计算结果更符合真实情况，但计算结果和渗透系数采用常数的计算结果相差并不大，一般在进行数值计算时可以把渗透系数看为常数。吹填土的初始孔隙比相对较大，在真空荷载下孔隙比会发生很大变化，若仍采用渗透系数为常数计算吹填土的固结变形，其结果将产生较大的偏差。在进行真空荷载下吹填土地基的有限元固结分析时，尚无学者考虑渗透系数随孔隙比的非线性变化关系。

本文通过室内真空模型试验，获得真空荷载下土体变形规律，并把这些规律应用到有限元计算中。文中采用修正的剑桥模型，并考虑渗透系数随孔隙比非线性变化，对模型槽试验模型进行数值模拟，其计算结果与实测结果吻合。分析了距排水板不同位置处土体孔隙比和渗透系数的变化规律，并对比分析了k为常数对真空荷载下吹填土固结变形计算的影响。

1 真空模型试验

1.1 试验概况

真空模型试验的主要试验装置由常规三轴仪改装而成，可以称它为负压固结仪，负压固结仪的管路连接方式如图1所示。压力室中土样为圆柱形，尺寸为φ39.1mm×80mm，试样上下两端抽真空；真空荷载大小可以通过调压器控制；负压固结仪可以量测土样单位时间的体积变化量和轴向变形。

图1 负压固结仪示意图

真空模型试验进行3组试验，初始含水率分别为92%、80%和70%，土样取自天津港某钻孔，测得土样的比重为2.74，塑、液限分别为28%和51%。土样的制作及其安装参考GB-T 50123—1999《土工试验方法标准》。

本试验对土样进行5级分级加荷，分别为10 kPa、25 kPa、40 kPa、60 kPa、80 kPa。首先对土样施加10 kPa的负压，并量测土样单位时间内体积变化量和轴向变形，待土样在10 kPa负压下固结稳定后，再加下一级真空荷载，稳定标准为每小时体积变化量小于0.1ml，依次进行加载。真空泵提供负压源，真空荷载大小由调压器进行调节，并通过真空表2监测对土样施加真空荷载的大小。

1.2 试验结果

实验结束后，试样的形状和物理状态产生很大的变化。试样发生相当大的收缩变形，上下两端变形基本一致，试样由圆柱形变为中间细、两头粗的土柱。这是因为土体受到收缩的体应力，两头的土体又受到透水石的侧向约束作用。3组试样的含水率分别降为48%、46%、46%，含水率均降到了液限以下，试样由最初的流塑状态变为软塑状态。土样变得密实，具有黏性，抗剪强度增大，土样的物理力学性状得到了很大的改善，加固效果非常明显。

土样的e-ln p曲线如图2所示。不同初始含水率的土样，在10 kPa负压作用下固结稳定后，土样的孔隙比相当接近；试样在负压下的压缩曲线与正压下的压缩曲线有相同的规律，即e随ln p基本呈线性递减趋势，不同初始含水率的试样压缩曲线非常接近，可以认为孔隙比与有效应力具有一一对应关系。因此，在对吹填土进行有限元计算时，本构关系宜选择能反映此规律的修正剑桥模型，图2中e-ln p的曲线斜率即为模型参数λ。

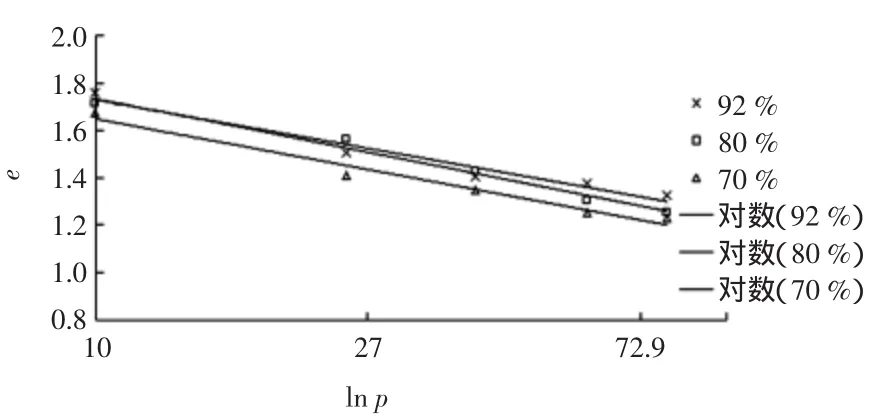
图2 真空荷载试验e-ln p曲线

从图2还可以看出，土样的孔隙比变化很大，变化最大的是初始含水率为92%的土样，初始孔隙比为2.52，试验完成后孔隙比变为1.32，差值达1.2。孔隙比变化如此之大，渗透系数也会随着发生很大的变化。试验结果表明对于吹填土的固结分析，很有必要考虑渗透系数随孔隙比非线性变化关系。

2 模型槽试验及有限元计算

2.1 模型槽试验

模型槽试验装置由模型槽、密封材料、真空系统和量测系统组成。模型槽由钢板和钢构架焊接而成，刚度相对很大，模型槽在真空荷载作用下不会发生侧向变形。密封材料包括土工布和密封膜，铺设于砂垫层之上。真空系统由真空泵、砂垫层、排水板组成，真空荷载通过砂垫层和排水板施加于吹填土。真空表和孔压传感器组成了量测系统，真空表量测砂垫层和不同深度处土体的真空度，孔压传感器量测吹填土表面下不同深度处土体的孔压值。

模型槽的尺寸为1.2m×1.2m×1.5m，吹填土的体积为1.2m×1.2m×1.1m，土样的初始含水率为85%。首先向模型槽中分层注入泥浆，然后在吹填土中设置排水板、真空表、孔压传感器，其中排水板间距为30 cm，孔压传感器和真空表设置在吹填土表面下30 cm、60 cm、90 cm处，在吹填土表面铺设10 cm的砂垫层，埋设真空表，连接真空管路，铺盖土工布和密封膜，最后开启真空泵进行试验。试验模型如图3所示，试验过程中定时记录不同深度处真空表和孔压传感器的读数。

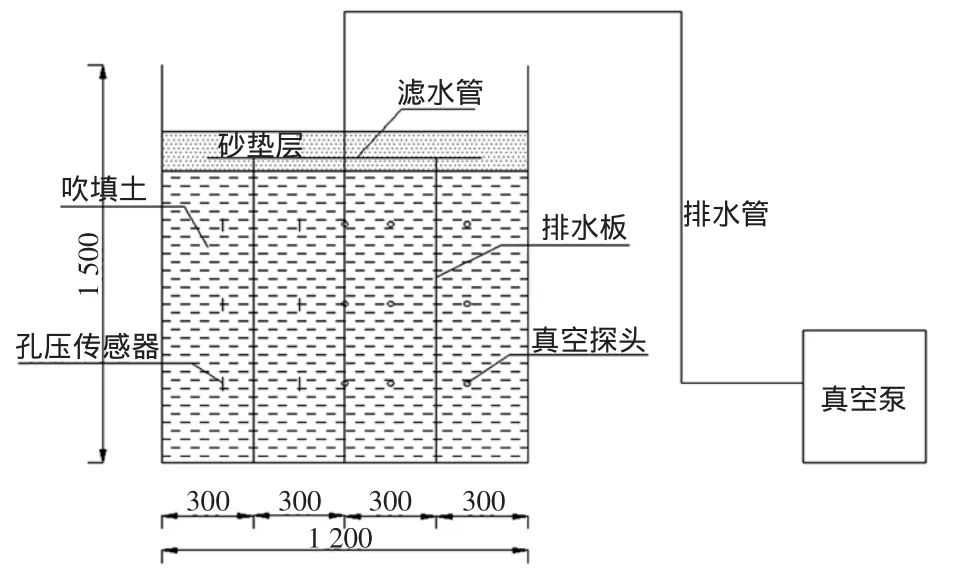
图3 真空预压模型槽试验简图

根据真空表的监测结果，膜下真空度在开始阶段上升很快，2 h就达到了60 kPa，5 d后达到90 kPa左右。通过真空表读数发现，排水板中真空度随深度递减，但由于吹填土深度不大，膜下真空度与吹填土表面下90 cm处排水板的真空度差值一般在5 kPa以内，故在进行真空固结计算时可以不考虑排水板中真空度随深度的变化。

吹填土表面下30 cm、60 cm、90 cm处土体的孔压（超孔压）量测结果如图4所示。从孔压与抽真空时间变化曲线的变化趋势看。在抽真空开始阶段，孔压值下降的很快，在40 h内孔压可以降到-10 kPa以下；当抽真空到40 h左右的时候，孔压变化缓慢，出现一个“放缓段”；直到抽真空100 h左右，孔压变化再次加快，孔压值呈平稳变化趋势；到480 h左右，孔压值趋于稳定。不同深度土体的孔压值随抽真空时间变化曲线，总体变化趋势相同，但深度越浅、孔压值变化相对越大。由于排水板弯折、淤泥阻塞土工布、真空度衰减等因素的影响，各点土体的孔压值大小在试验完成时均不能达到膜下真空度，且有25～35 kPa的差距。

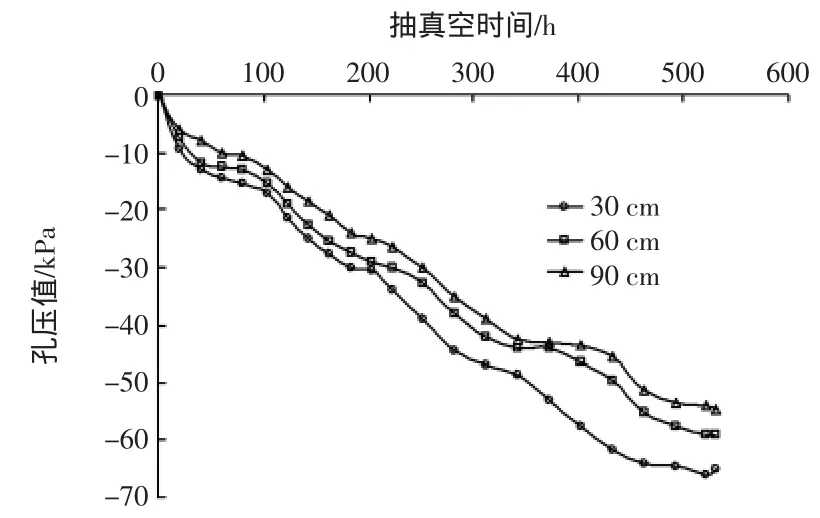
图4 不同深度处土体孔压值随抽真空时间变化曲线

2.2 有限元计算中本构模型的选取及渗透系数的设置

在土体的有限元计算过程中，本构模型的选取对计算结果影响很大。软土变形具有非常明显的非线性和硬化特征。根据本文的真空模型试验结果绘制土样的压缩曲线，土样的孔隙比e随ln p有线性减小的规律。故在计算时本构关系选用具有非线性和硬化特征的修正剑桥模型[8]。其屈服轨迹为：

式中：M为q-p′平面上破坏线的斜率；p′为体积应力；q为偏应力；p0′为硬化参量。

在真空荷载作用下，随着土体有效应力的增长，孔隙比不断减小，土体变得密实，渗透系数不断减小，当土体孔隙比变化较大时，不考虑渗透系数随孔隙比的变化将对计算结果带来较大的影响。顾慰慈[9]指出在相同的固结时间内，考虑土的渗透系数变化和不考虑土的渗透系数变化所计算的孔压值相差可达两倍以上。

本文采用Taylor提出的线性e-log k关系定义土体的孔隙比e和渗透系数k的关系。虽然不同的学者对渗透系数与孔隙比的关系提出了多种关系式，并在软黏土中都有一定应用，但目前在软土工程中应用较多的是Taylor[10]提出的线性elog k关系，它能很好地描述大多数天然软土的特性，即：

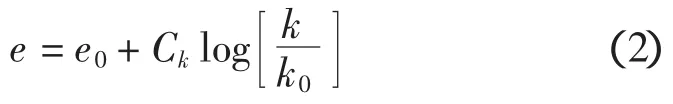
式中：e0为初始孔隙比，k0为初始渗透系数；Ck为e-log k曲线的斜率，一般情况下Ck=0.5 e0。

2.3 计算模型的建立

模型槽中排水板正方形布置，按分担的影响面积等效的圆直径为de=1.13s。本文建立轴对称模型，模型的深度为1.1m，半径r=17 cm。计算中对排水板进行如下简化处理：排水板简化为一条直线，不考虑砂井的涂抹作用和真空度随排水板深度的递减，负压沿排水板均匀分布，排水板的真空度与膜下真空度相同。计算模型的位移边界条件为：固定土体的下表面，限制土体的横向变形。孔压边界条件：排水板与土体上表面为负压边界，下表面与四周均不透水。

本文使用ABAQUS软件来研究单个排水板周围土体在真空荷载下的固结规律。计算模型的本构关系采用修正的剑桥模型，并考虑渗透系数随孔隙比变化。计算模型的计算参数如表1所示。真空荷载通过排水板和吹填土上表面施加于土体，通过设置土体的孔压边界条件为负值来实现。真空荷载大小按试验量测结果施加，真空荷载随时间变化关系如图5所示，实际计算时，加载时间有所延长。

表1 模型槽模型有限元计算参数

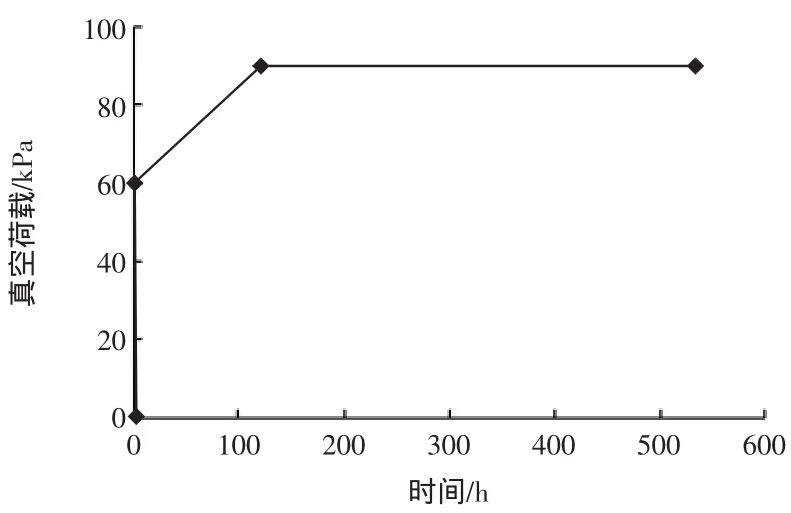
图5 真空荷载加载示意图

2.4 计算结果

吹填土表面下30 cm、60 cm处土体的孔压（超孔压）实测值与模拟值如图6所示，为了能够显示完整的固结曲线，计算模型真空荷载的加载时间延长到1389 h。从图中可以看出，有限元模拟值与实测值比较接近，有相同的变化趋势。均表现为孔压在土体固结前期变化很快；在40 h左右进入“放缓段”，到100 h左右的时间，孔隙水压力变化再次加快；但是在抽真空后期，实测值趋于稳定，模拟值仍有下降的趋势，仍需要较长的时间才能固结稳定。这是因为在实际抽真空情况下，真空传递会受到排水板弯折[11]、淤泥阻塞土工布、真空度衰减等因素的影响，造成真空度传递受阻，有限元模拟没有考虑这些因素的影响。总体来看，采用该模型能够很好地模拟吹填土在真空荷载下的变形规律。

图6 吹填土表面下土体孔压值随抽真空时间变化曲线

吹填土表面下30 cm处土体孔隙比随抽真空时间变化曲线如图7所示。距排水板不同距离的土体孔隙比随抽真空时间具有不同的变化趋势。距排水板0.5 cm处土体的孔隙比在开始阶段变化很大，在3 h内从2.33降到1.70，随后孔隙比变化放缓，200 h后孔隙比趋于稳定。距排水板17 cm处土体孔隙比在抽真空的初期，孔隙比变化相对较小，52 h内孔隙比变化很小；52 h后孔隙比变化加快；到抽真空154 h时，孔隙比变化曲线呈由陡变缓的趋势，到700 h后趋于稳定。吹填土在整个固结过程中孔隙比变化很大，贴近排水板土体在短时间内被压密，较远处土体逐渐被压密。

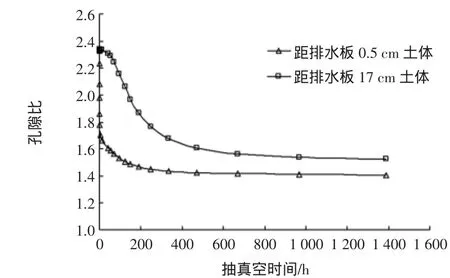
图7 吹填土表面下30 cm处土体孔隙比随抽真空时间变化曲线

在真空荷载作用下，土体不断被压密，渗透系数也随之发生变化。在真空荷载作用的不同时刻，吹填土表面下30 cm处不同位置土体的渗透系数如图8所示。抽真空进行2 h，距排水板0.5 cm处土体渗透系数变化很大，渗透系数由7.4×10-9m/s降到2.3×10-9m/s，下降达69%之多，其它位置土体的渗透系数变化较小或没有变化。在抽真空2～25 h阶段，不同位置处的渗透系数都有所降低，中间位置土体渗透系数变化较大，距排水板0.5 cm和17 cm处土体渗透系数变化较小。在抽真空25～123 h阶段和123～470 h阶段，除距排水板0.5 cm处土体外，其它位置土体的渗透系数均有较大变化，距排水板17 cm处土体的渗透系数从 7.4×10-9m/s降到 1.8×10-9m/s。在抽真空470～1389 h阶段，各位置土体的渗透系数变化均很小，变化值不大于0.3×10-9m/s。排水板周围土体由近及远逐渐被压密，在不同的固结阶段，不同位置处土体的渗透系数有不同的变化规律，且在某个时间段内，可能发生很大变化或没有变化，故在吹填土固结计算中考虑渗透系数变化是非常有必要的。

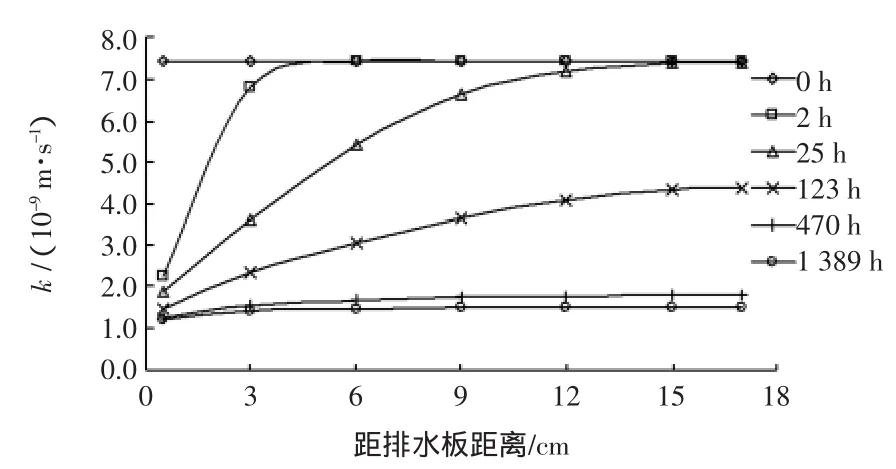
图8 吹填土表面下30 cm处不同位置土体渗透系数

为了研究渗透系数对固结过程的影响，本文还建立了渗透系数在真空预压期间为常数的计算模型，其它条件保持不变，k取土体固结前后渗透系数的平均值。两模型计算的固结度如图9所示。在开始阶段，两模型计算结果相差不大；5 h后k为常数模型的固结速率明显比k变化模型快；t=50 h时，k变化模型固结度为20%，k常数模型固结度达到40%，常数模型的固结度是k变化模型的2倍；t=300 h，k为常数模型土体基本完成固结，而k变化模型固结度仅达到64%；t=1200 h时，k变化模型固结基本稳定，所用时间是常数模型的4倍。从整体看，两计算模型固结度相差较大，k为常数模型计算土体固结始终较快。这是因为距排水板0.5 cm处土体在2 h内渗透系数降低到2.3×10-9m/s，仅接近平均渗透系数4.45×10-9m/s的一半，孔隙中的水绝大部分是通过排水板排出的，孔隙水排出快慢是由排水通道中最细处决定的，贴近排水板土体的的渗透系数小是k变化模型固结相对较慢的主要原因。

图9 不同计算模型固结度随时间变化曲线

根据模型槽试验的实测结果（图4），t=300 h时，各个深度的孔压仅达到40 kPa左右，孔压还有很大的下降趋势，还需要很长的时间才能固结稳定。k为常数模型在t=300 h时土体基本完成固结，计算结果与实际情况有很大的差异。故在进行吹填土地基固结计算时，考虑渗透系数变化对固结过程的影响是非常必要的。

3 结语

通过真空模型试验和对单个排水板周围土体进行真空预压有限元分析。研究吹填土孔压、孔隙比以及渗透系数的变化规律。对比分析k为常数计算模型与k变化模型的计算结果。得到如下结论：

1）高含水率的吹填土在负压下的压缩曲线具有规律性，即e随ln p呈线性递减。吹填土在真空荷载作用下固结，孔隙比变化很大，在进行固结计算时应考虑渗透系数随孔隙比变化。

2）采用修正的剑桥模型，并考虑渗透系数随孔隙比非线性变化关系，建立模型槽试验计算模型，其计算结果与实测值有较好的吻合，该计算模型适用于真空预压下吹填土地基的固结计算。

3）在真空荷载作用下，排水板周围土体由近及远逐渐被压密，渗透系数也随之发生很大的变化；贴近排水板处土体在很短时间内被压密，较远处土体逐渐被压密。贴近排水板的土体渗透系数控制着吹填土的固结速率。因此，采用k为常数的模型计算的固结度比k变化模型大，在较短的时间内固结稳定，这与实测结果有很大的偏差，故在进行真空预压下吹填土地基固结计算时，考虑渗透系数随孔隙比非线性变化是非常必要的。

[1] 成玉祥.滨海吹填土结构强度形成机理与真空预压法关键技术研究[D].西安：长安大学，2008.

[2] 董志良，张功新.天津滨海新区吹填造陆浅层超软土加固技术研发及应用[J].岩土力学与工程学报，2011，30（5）：1073-1080.

[3] 钱家欢，殷宗泽.土工原理与计算[M].北京：中国水利水电出版社，1996：229-237.

[4] 闫澍旺，陈环.用真空加固软土地基的机制与计算方法[J].岩土工程学报，1986，8（2）：35-44.

[5] 董志良，陈平山.真空预压下软土渗透系数对固结的影响[J].岩土力学，2010，31（5）：1452-1456

[6] 余湘娟，吴跃东，赵维炳.真空预压法对加固区边界影响的研究[J].水利学报，2002（9）：123-128.

[7] 彭劼，刘汉龙.真空-堆载联合预压法软基加固对周围环境的影响[J].岩土工程学报，2002，24（5）：656-659.

[8] 郑颖人，孔亮.岩土塑性力学[M].北京：中国建筑工业出版社，2010：246-255.

[9] 顾慰慈.考虑渗透系数变化时土石坝的固结计算[J].河北水利水电技术，1998（4）：13-16.

[10] TAYLORD W.Fundamentals of Soil Mechanics[M].New York：John Wiley and Sons Inc，1948：700.

[11] 闫澍旺，孙立强，李伟，吴坤标.真空加固超软土工艺的室内模型试验研究[J].岩土工程学报，2011，33（3）：341-347.