Gilbert算法研究及其改进*
2013-03-11汪卫兵刘秉瀚
汪卫兵,刘秉瀚
(福州大学 数学与计算机科学学院,福建 福州350108)
Gilbert算法[1]是一种求解最接近点对算法,即求解凸包外指定点到一群点集组成的凸包的距离,广泛应用于机器人领域。Gilbert算法是一种迭代算法,属于梯度下降算法,具有很好的全局收敛性,易被计算机实现,而且适用几何的观点来分析。但是,Gilbert算法的缺点也很明显,特别是接近最优解时收敛过慢。
针对Gilbert算法的改进算法有MDM算法[2]、NPA算法[3]以及CHANG L[4]等人提出的改进算法。MDM算法利用具有消极影响的训练样本点改进更新策略,在迭代过程中,一旦发现迭代点的组合中具有消极影响的训练样本点,就直接在迭代点的线性组合中删除或是降低该点对目标函数的影响,并同时使得目标函数边缘下降。MDM算法解决了Gilbert算法接近最优解时收敛过慢的问题,但仍需要多次迭代完成计算。NPA算法结合了Gilbert算法和MDM算法的特点,选取三角形区域作为迭代点的搜索范围,扩大了迭代点的搜索范围,实验结果显示,它比MDM算法收敛更快,但NPA算法仍存在计算量很大的不足。参考文献[4]的研究证明了最接近点对问题的最优解一定出现在凸包顶点中两点组成的边上或者几点确定的面上,根据此结论,最优解一定落在凸包边界上。CHANG L等人据此提出了一种改进的Gilbert算法(下文简称CQW),当算法迭代到一定次数时,如果发现算法重复选取几个凸包顶点作为算法迭代选取的顶点,就直接计算凸包外指定点到这几点组成的平面或两点组成的线段的距离,它加快了Gilbert的收敛,但需要人工设置迭代次数,迭代次数的选取是一个难点。
针对上述算法计算量大的问题,本文分析了Gilbert收敛慢的原因,当新的迭代点越来越趋近于最优解时,它一直在最优解附近徘徊,不能快速到达凸包边界。本文通过实验发现,在迭代的过程中,一旦迭代点出现在凸包的边界上,Gilbert算法会快速收敛。据此,本文在Gilbert算法的基础上提出一种新的迭代策略,迭代过程中将Gilbert算法原有的梯度方向上的候选点与凸包边界上的候选点进行比对,选取离凸包外指定点更近的候选点作为新的迭代点,这样的迭代机制一有机会即将迭代点拉到凸包的边界上,有效避免了在凸包内部最优解附近不停徘徊迭代的情况发生,减少迭代次数,加快收敛速度。实验结果表明,本文改进后的算法与NPA算法相比,计算量小,问题的求解速度更快,与CQW算法相比,不需要人工设置迭代次数,更容易求出最优解。
1 Gilbert算法
1.1 最接近点对问题

最接近点对问题(NPP问题)的目标就是找到两个凸包间的最接近点对,即:

Z=U-V表示凸包U和V的明可夫斯基差,凸包Z有s1×s2个顶点,最接近点对问题转化为在凸包Z上找到离凸包外指定点(为方便阐述,凸包外指定点默认为坐标轴原点)最近的点(MNP问题),即:

1.2 算法步骤
Gilbert算法原本解决的是MNP问题,在凸包U上找到离原点最近的点。下面给出一些相关的数学定义[5]:
定义1:设U为Rm的一个凸包,y∈U,称

为U上的支持函数。
定义2:设S(y)是Rm上的一个函数,称

为Rm上的关联函数。S(y)为U的一个顶点。
Gilbert算法具体步骤如下:
(1)初始化。取t=1,在凸包U上任取一点z1,z1∈U,设定停止精度ε。
(2)按式(7)进行梯度下降局部优化迭代更新。

其中zt+1为zt和S(-zt)组成的线段上离原点最近的点,更新力度:

(3)如果满足条件||zt||2-||zt+1||2<ε,则算法停止,否则令t=t+1,转步骤(2)。
Gilbert算法首先任取一个样本点z1,通过式(6)确定与z1反向量内积最大的凸包顶点S(-z1),判断S(-z1)是否与z1靠得很近,如果是,则停止;否则,按式(7)进行局部更新,即在S(-z1)和z1连线上求取离原点最近的点(这个更新操作可以保证zt+1的范数严格小于zt的范数),如此反复,最终获得凸集U的最小范数点。
1.3 Gilbert算法的收敛问题
如图1所示,三角形ABC为一个平面凸包,O为原点(即凸包外指定点),选取P1作为算法的初始点,迭代点依次沿着P2、P3、P4更新,最终到达离O点的最近点Pn。在Pi(i=1,2,…,n)迭代的过程中,与向量Pi内积最小的顶点一直是B点或者C点,最终问题的解落在线段BC上。Gilbert算法计算O点到三角形ABC的求解迭代过程如图2所示,Gilbert算法迭代到一定次数后,迭代点一直在最优解附近徘徊,算法收敛速度非常慢,当设定停止精度ε=10-6时,算法迭代了489次。

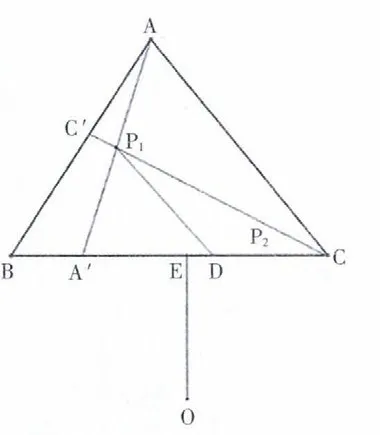
图3 迭代搜索范围
算法迭代搜索范围如图3所示,AA′和CC′相交于P1点,P1D平行于AC,OE与BC垂直。在第 一次迭代过程中,线段P1C是Gilbert算法迭代点的搜索范围,Gilbert算法只计算与向量P1内积最小的顶点C,而MDM算法还计算了与向量P1内积最大的顶点A,P1D平行于AC,让P1点沿着P1D方向偏移,线段P1D是MDM算法迭代点的搜索范围。NPA算法结合了Gilbert算法和MDM算法的优点,考虑了4种搜索范围:(1)三角形P1DC;(2)三角形P1A′C;(3)四边形ACA′C′;(4)三角形ABC。这4种情况都包含了Gilbert算法和MDM算法的搜索范围,NPA算法认为(1)和(2)两种情况优于Gilbert算法和MDM算法,(3)和(4)两种情况搜索范围太广,比MDM算法的效果差。第(1)种情况收敛速度比MDM算法快,第(2)种情况比第(1)种情况收敛速度更快。因此,NPA算法选取三角形P1A′C作为迭代点的搜索区域,扩大了迭代点的搜索范围,有利于找到更优的迭代点,同时加快了收敛速度。CQW算法依然采用Gilbert算法的更新策略,当迭代K次(K的选取是人为设置的)后,发现算法重复选取几个凸包顶点作为算法迭代时选取的顶点,就直接计算O点到这几点组成的平面或两点组成的线段的距离,减少了迭代次数。
1.4 Gilbert算法收敛慢的原因分析
如图4所示,矩形ABCD是一个平面凸包,O为原点。利用Gilbert算法求解点O到凸包的最短距离时,选取初始点P1进行第一次迭代后,与P1点内积最小的顶点为D点,然后求出O点到线段P1D上的最近点P2,并将其作为新的迭代点。图4中若∠P1DO>90°,则P2点就是D点,而D属于凸包的边界,算法很快收敛,找到最优解。若∠P1DO<90°(如图5所示),则迭代点P2出现在凸包的内部,Gilbert算法会在凸包内部不停地选取迭代点,很难到达凸包的边界,算法收敛速度非常缓慢。

图4 迭代点出现在凸包边界

图5 迭代点在凸包内部
凸包边界由边和面组成,根据CHANG L[4]等人的结论,最优解一定落在凸包边界上。本文通过多次实验发现,算法迭代点到达凸包边界之后就会快速收敛。因此,本文考虑每次选取迭代点时都与离O点最近的凸包边界线段上的点作比较,尽可能将迭代点拉至凸包边界上,这样可避免算法在凸包内部最优解附近徘徊迭代,以此来改进Gilbert算法的收敛速度。
2 本文方法
2.1 算法思路
本文基于1.4节的分析,在算法第一次迭代确定顶点D之后(见图5),考虑包含D的凸包边界线段AD和CD,选择离O点最近的边界线段AD,同时将P1D和AD这两条边作为迭代点的搜索范围,分别计算O点到这两条线段的最近点,选取两者中较近的点作为新的迭代点:如果O点到AD边更近,则选取O点到AD边上最近点作为新的迭代点;如果O点到Gilbert算法原来的迭代点更近,则选取原来的迭代点作为新的迭代点。这样每次迭代都有机会将迭代点拉到凸包边界,可避免Gilbert算法不停地在凸包内部最优解附近选取迭代点,使得算法快速收敛。
2.2 算法步骤
本文改进后的算法步骤如下:
(1)初始化。取t=1,在凸包U上任取初始迭代点z1,z1∈U,设定停止精度ε。
(2)按式(7)得到迭代候选点z′。如果z′∈X(X为凸包U的顶点集合),则zt+1=z′,令t=t+1,转步骤(3)继续执行;如果z′∉X,按式(8)求S(-z′)和S(-zt)组成的线段上离O点最近的点z″。

令t=t+1,转步骤(3)继续执行。
(3)检验停止条件。如果满足条件||zt||2-||zt+1||2<ε,则算法停止,否则转步骤(2)。
如图6所示,z1是算法选取的初始点,在迭代过程中,先计算出与向量z1内积最小的顶点C,即S(-z1),计算O到线段z1C的最近点z′。

图6 本文算法迭代过程
如果z′∈X,则表示新的迭代点是凸包的顶点,按照Gilbert原算法执行迭代。如果z′∉X,计算与向量z′内积最小的顶点B,即S(-z′),计算O到BC的最近点z″。
比较z′和z″,取两个距离中较小的垂足作为新一轮的迭代点。这样可以保证每次选取的迭代点到O点的距离小于或者等于Gilbert算法中的迭代点到O点的距离,Gilbert算法已被证明是收敛的,这样可以保证本文算法的收敛性。
本文算法每次选取迭代点时都与离O点近的边界线段上的点作比较,有效避免了在凸包内部最优解附近不停地选取迭代点这种情况的发生,可以减少算法的迭代次数,加快收敛速度,提高计算效率。
3 实验结果及分析
为了证明本文算法迭代策略的有效性,将本文算法与CQW算法、NPA算法进行实验对比。设X=100×rand(50,3),这是一个50乘以3的随机数矩阵,它表示50个点,每个点的各个坐标值均介于0~100,U是由这50个顶点构成的凸包,利用上述3种算法求解坐标轴原点O到凸包的最短距离,设置算法停止精度为10-10,由于精度较高,Gilbert算法很难求出最优解,CQW算法需要人为设定迭代次数,这里设定为100次,3种算法执行时间和迭代次数的比对结果如表1所示。求解的最终结果均为32.813 134 341 830 660。

表1 实验结果比对
实验证明,本文算法与CQW算法相比,减少了迭代次数,加快了收敛速度;与NPA算法相比,提高了计算效率和计算速度。
本文针对Gilbert算法的缺点对其进行了改进,解决了Gilbert算法收敛过慢的问题,可以非常高效地求解MNP问题,改进后的Gilbert算法与Gilbert算法一样,可用于NPP问题,将具有更强的普适性。实验证明,本算法与其他算法相比具有以下优点:(1)算法的迭代次数不需要人为控制,依然可以快速收敛;(2)算法的执行速度较快,最优解的搜索范围比NPA算法更优;(3)算法非常有效地避免了迭代点在凸包内部不停迭代的情况。改进后的Gilbert算法可以用于支持向量机的数据分类、碰撞检测、机器人路径规划等领域。同时,它可以用作支持向量机的训练算法,这是下一步将要展开的工作。
[1]GILBERT E G.An iterative procedure for computing the minimum of a quadratic form on a convex set[J].SIAM Journal of Control,1966,4(1):61-79.
[2]MITCHELL B F,DEM'YANOV V F,MALOZEMOV V N.Finding the point of a polyhedron closest to the origin[J].SIAM J.Contr.,1974,12:19-26.
[3]KEERTHI S S,SHEVADE S K,BHATTACHARYYA C,et al.A fast iterative nearest point algorithm for support vector machine classifier design[J].IEEE-NN,2000,11(1):124.
[4]CHANG L,QIAO H,WAN A,et al.An improved Gilbert algorithm with rapid convergence[C].Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems,Beijing:2006:3861-3866.
[5]周志华.机器学习及其应用2007[M].北京:清华大学出版社,2007:62-63.
