菲索干涉仪中精确移相的实现

苏志德，史振广，彭 吉，隋永新* ，杨怀江

(1.中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室，吉林长春130033;2.中国科学院大学，北京100049)

1 引言

光学干涉测量技术是以光波干涉原理为基础，以光的波长为单位的一种计量测试方法，是检测光学系统、光学元件较为有效、准确的方法之一。其中，菲索型干涉仪具有共光路，系统误差较小的优点，常用于元件的面形测量［1］。1974年，移相技术的引入极大程度地提高了干涉仪的检测精度［2］，因此，移相式菲索干涉仪成为当前最常用的光学元件面形精度测量设备［3］。目前，市场上已有美国Zygo公司和ESDI公司生产的干涉仪出售，但具体技术报道较少。在国内，南京理工大学和成都精密光学工程研究中心等单位也对干涉检测技术进行了研究，并研制了原理样机，但其测量精度有待提高［4-7］。在高精度干涉仪方面，国内还处于起步阶段，因此，为打破国外公司在此领域的垄断地位，对高精度干涉测量技术开展研究是很有意义的。

在移相干涉仪中，移相误差的存在会极大地影响测量结果的准确性［8-12］，而移相误差的大小又取决于移相系统工作性能的优劣，因此，对能够实现高重复性和高精度测量的移相系统开展研究是很有必要的。本文建立了用于移相干涉仪的同步采集移相系统，并讨论了精确移相的具体实现方法，包括移相器移动速率的计算，移相器行进过程的详细设计和移相器的标定等。实验结果表明，该移相系统及移相方法具有较高的测量重复性和准确度，可满足纳米级面形测量的要求，为高精度移相干涉仪的研制奠定了基础。

2 移相系统的组成与工作原理

2.1 移相系统的组成

同步采集移相系统的框图如图1所示。该系统主要由PZT移相器、移相控制器、计算机、图像采集卡和CCD相机组成。移相控制器选用德国PI公司的E-712控制箱，它包括计算机通信模块、位移监测模块。控制模块和驱动模块，各模块相互配合完成PZT移相器的驱动和控制。PZT移相器内部集成有电容位移传感器，可以实时测量移相器的行进量并反馈至移相控制器的位移监测模块。NI公司的PCI-1433图像采集卡被选用，于实时采集CCD接收的干涉图像并传送给计算机，该图像采集卡具有外触发口，可以接收触发信号并根据配置执行单帧采集或多帧连续采集的任务。CCD相机选用Baumer公司的SXC 10相机，可以方便地设置曝光时间和帧速率大小。计算机用于配置移相控制器和图像采集卡，并完成对CCD相机的参数调节和图像显示、面形计算等功能。

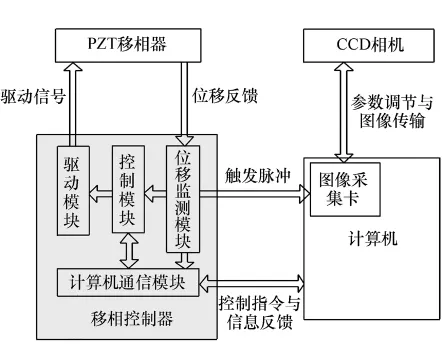
图1 同步采集移相系统框图Fig.1 Block diagram of synchronous acquisition phaseshifting system

2.2 移相系统的工作原理

移相系统的工作原理为:在面形测量之前，首先对CCD的帧频、曝光时间和移相器的起始位置及图像采集卡的触发条件进行初始化，图像采集卡此时处于预览模式，即只实时地显示接收到的图像但并不保存图像。开始测量时，图像采集卡切换到等待触发模式，移相控制器发送电压给移相器使之按照指定速度开始前进，并不断检测电容位移传感器的反馈值。当移相器到达某既定位置时，由移相控制器发出一电压脉冲给图像采集卡，图像采集卡收到脉冲后，按照给定的帧速率连续采集并存储满足移相算法要求的若干幅干涉图。然后，由计算机根据采集到的干涉图像进行面形求解。

3 精确移相的实现

3.1 移相速度计算

在连续式移相中，CCD相机是对图像进行连续积分并存储的。设CCD的帧速率为f，则CCD每采集一幅图像所需的时间为1/f。相位差β与光程差(OPD)的对应关系为:

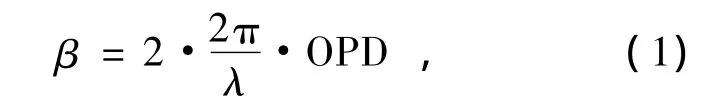
式中，OPD是单程的光程差，等同于移相器的行进量d。设移相算法要求相邻两干涉图间的移相值β为2π/N，代入上式可知此移相值对应PZT移相器的行进距离为:

所以计算可得测量所需要的移相器行进速率为:

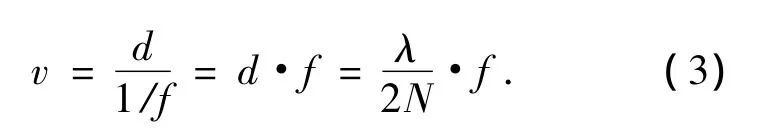
在632.8 nm波长下，以Zygo干涉仪中使用的13帧算法为例，该算法要求各帧间移相值为π/4，若CCD帧速率为60 frame/s，则对应的PZT的速度为:

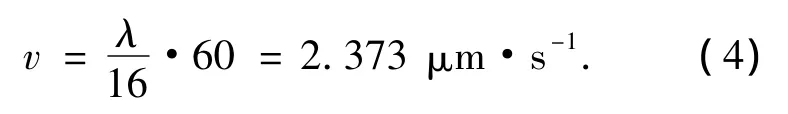
将此速度作为移相器的初始速度，在后续的移相器标定中对此速率做适当调整，即是移相器在测量过程中的行进速度。

3.2 移相器行进过程的设计

3.2.1 初始化移相器以减小离焦误差

如图2所示，当被测元件是球面时，参考面在B位置时与被测面是共焦位置，当PZT移相器推动参考面沿光轴平移到C位置时，就会出现一定的离焦量，从而引入测量误差。

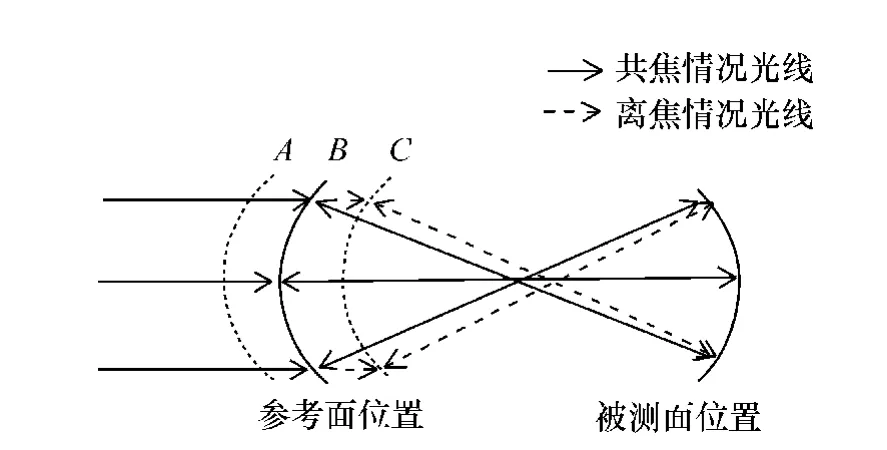
图2 球面干涉腔离焦示意图Fig.2 Schematic drawing of defocus in spherical cavity

在移相过程中需尽量减小此离焦量的值，以减小测量误差。本应用中，在PZT初始化时将其定位在位置B处，调整被测元件位置使干涉图达到零条纹状态，在开始测量时，移相器退回到A处，开始匀速运动，到达C位置时停止运动，保证CCD的采图的时刻分布在B位置的两侧，则可以减小由于存在离焦而造成的误差。实际中，通过对测量结果做Zernike拟合得到Power值，并使之为零，来指导PZT移相器的起始位置的确定。

3.2.2 避开加速段和减速段

在移相过程中，希望移相器是匀速移动的，但实际上它的移动可分为加速-匀速-减速3个阶段。因此，在CCD帧速率恒定的情况下，要保证PZT的移动处于匀速阶段，需要在行进过程中为PZT的加速段和减速段留出余量。如图3所示，设面形测量需要采集N帧干涉图，在N帧干涉图采集过程中，PZT移相器需要移动的位移为L，则令B1，B2对称分布在共焦位置B的两侧，与B的间隔是L/2，自A位置开始，在B1前为移相器留出充分的加速段，在B2后为移相器留出充分的减速段，到C位置结束。本应用中，将加速段和加速段设为1 μm，满足了应用的需求。

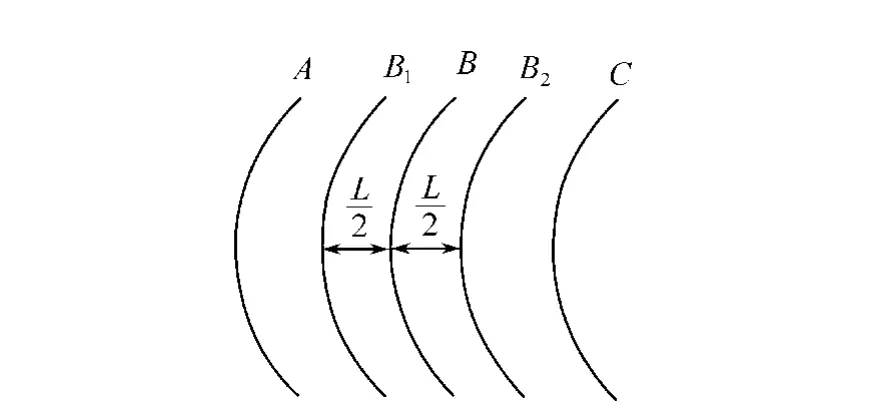
图3 移相器移动过程示意图Fig.3 Skematic of moving process of phase shifter

这样，PZT移相器的行进过程可描述为:在初始化时，将PZT移相器定位在B位置，当光路调整完毕开始面形测量时，移相器退回到A位置处，开始以设定的速率向前移动。到达B1位置时，控制器发出一脉冲至图像采集卡，通知采集卡开始采图，移相器到达B2位置时采集卡采图完毕，移相器继续移动一段位置，到C处停止，从而测量过程结束，整个过程的位移检测由电容位移传感器来完成。当需要做多次重复测量时，移相器移动到C位置后以很快的速度回到A位置，再按照设定速度开始移相到C，循环执行即可。

3.3 移相器的标定

实际工作中，PZT移相器的行进速度不会严格按照既定速度来行进，并且PZT在移相中移动方向可能会与光轴有夹角，所以要对移相器进行标定，根据求解的移相值调整移相器的行进速度和安装姿态使其达到最佳的移相效果［13-14］。本实验室有一台较旧的干涉仪，该干涉仪移相功能无法使用，但光机系统完好。对此干涉仪进行了改造，换上新的移相器和CCD相机，开展对移相器性能的标定。由于当前移相器的线性度较好，所以选用基于移相算法的标定算法来求解移相值，表达式为:

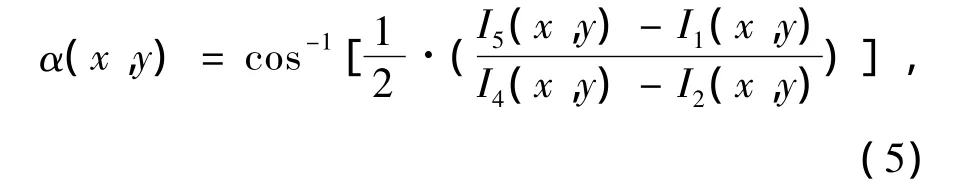
式中:I1(x，y)，I2(x，y)，I4(x，y)，I5(x，y)分别是采集到的第1、2、4、5 幅干涉图在(x，y)点的光强值，α(x，y)是计算得到的(x，y)点对应的平均移相值，计算时将上式中分母比较小的像素点去除，以避免奇异点的存在对计算结果的影响。在该标定方法中，如果得到的柱状图以预期移相值为中心对称分布，但比较平缓，说明移相器在移相中行进方向与光轴产生了夹角，需要对移相器的端面进行调整。如果得到的柱状图比较尖，但对称中心偏离预期移相值，说明移相速率不准确，需要增大或减小移相速率。在实验中，干涉图应尽可能调到零条纹，以减小由于倾斜和离焦对实际移相值的影响。选取连续采集的5幅干涉图如图4所示，其移相间隔为45°。

图4 移相器标定中的一组干涉图Fig.4 A group of interferograms for calibration of phase shifter

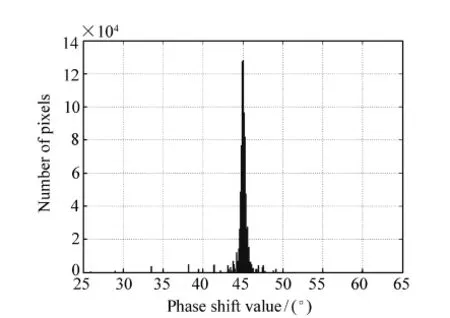
图5 移相器标定结果Fig.5 Calibration result of phase shifter

通过对PZT移相速率和安装姿态进行若干次调整，得到的移相相标定结果，如图5所示。

经过标定后，移相速率最终确定为2.380 μm，干涉图上各点的移相间距平均值为44.97°，标准差为0.91°，满足了应用需求。

4 实验验证

4.1 测量重复性试验

为验证使用该移相系统的重复性，在改造后的干涉仪上开展了重复性测量实验。干涉仪放置在有隔振地基的大理石平台上，用纸带将干涉腔罩住以减小空气扰动对测量结果的影响。在测量条件不变的情况下，对同一光学元件重复测量50次，用面形RMS的标准差来表示测量的简单重复性，测量50次得到的面形RMS分布如图6所示。

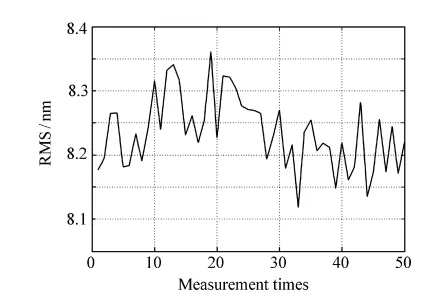
图6 50次连续测量的RMS分布Fig.6 RMS distribution of 50 consecutive measurements

计算可得，50次面形测量结果的标准差为0.055 8 nm，所以此移相系统的RMS简单重复性(1σ 值)为:

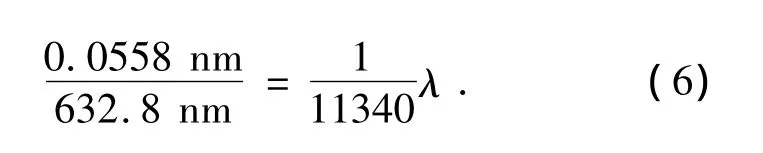
对50次测量结果取平均作为面形均值，然后将此50次测量结果与面形均值点对点做差，得到对应的50个差值面形，计算可得此50个差值面形的 RMS的平均值为 0.53 nm，标准差为0.08 nm，所以此移相系统的波前重复性为:

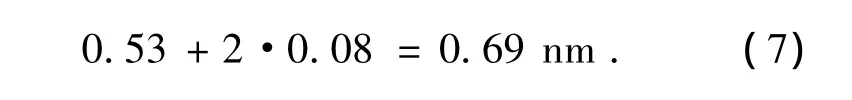
4.2 干涉仪测量精度验证

为验证利用此移相系统的测量精度，将改造后的干涉仪与Zygo公司的Verifire XP/D干涉仪做了测量比对实验。为减小由于环境影响及装夹不一致等因素引入的误差，两台干涉仪正对着放置，Verifire XP/D上安装15 cm(6英寸)转10 cm(4英寸)的转接板，将两个10 cm(4英寸)的标准平面镜分别装在两个干涉仪上进行对比测量。实验中，当用其中一台干涉仪做测量时，用纸片挡住另一个干涉仪中从准直镜出来的光束，以避免杂散光对测量结果的影响。实验装置示意图及实验照片如图7(a)、(b)所示。在改造的干涉仪上使用的是自主编制的面形计算软件，该软件使用与Verifire XP/D干涉仪一样的移相算法来计算面形。在两台干涉仪上分别做50次连续测量，然后将对应的面形测量结果点对点做差值，并分别计算此50个差值的RMS值，统计可得此RMS的均值为0.856 nm，标准差为0.036 nm，说明改造后干涉仪的测量结果与Zygo干涉仪的测量结果有很好的一致性。其中一组测量结果及其差值如图8所示。

图7 测量精度对比实验示意图及照片Fig.7 Schematic diagram and photograph of comparative experiment for measurement accuracy

从图8中可以看出，两干涉仪测量结果的PV值差别较大，这主要是由边缘处存在一些毛刺造成的。测量结果之差的RMS值约为0.9 nm，该差别可能是由于两台干涉仪的系统误差不一致造成的。

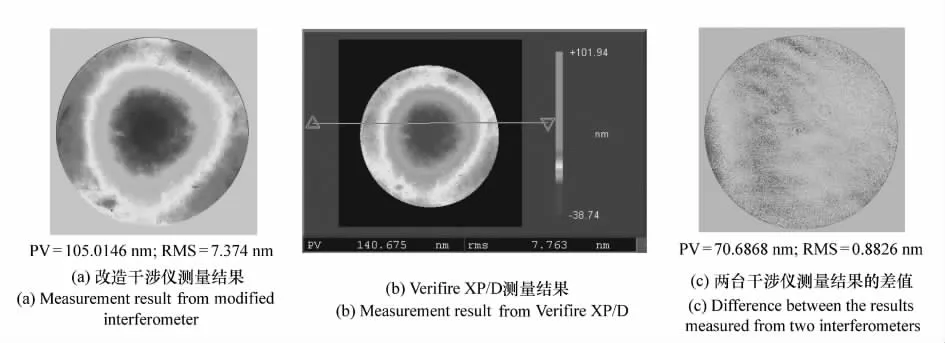
图8 两台干涉仪测量结果图Fig.8 Measurement results of two interferometers

为了验证此移相系统测量球面元件的精度，在图7所示的装置上换上两个f数为1.5的TS镜来开展测量。同样是分别在两台干涉仪上做50次连续测量，并将对应的面形测量结果点对点做差值，计算可得此50个差值的 RMS均值为0.947 nm，标准差为0.049 nm。可见，在测量球面元件时，利用此移相系统同样可以获得与Zygo干涉仪近似一致的测量结果。

5 结论

本文建立了适用于移相式干涉仪的同步采集移相系统，并对PZT移相器的具体应用进行了研究。在完成移相功能的同时，详细设计了移相器的行进过程，以减少在球面测量中的离焦误差和移相误差，并利用移相标定技术对移相器的速度进行了校正。通过在改造后的干涉仪上开展面形测量试验可知，利用该移相系统和移相方法可以获得λ/11 340的简单重复性和0.69 nm的波前重复性，将此改造后干涉仪与Zygo的Verifire XP/D干涉仪做了比对测量试验，结果显示:相同的平面和球面元件下两者测量的面形RMS之差的均值分别为0.856和0.947 nm，表明此移相系统及移相方法在重复性和准确度方面都能满足纳米级测量的要求，可以在高精度干涉仪中实现精确移相的功能。

［1］ MALACARA D.Optical Shop Testing［M］.New York:John Wiley＆ Sons Inc.，1994:17-33.

［2］ BRUNING J H，HERRIOTT D R，GALLAGHER J E，et al..Digital wavefront measuring interferometer for testing optical surfaces and lenses［J］.Appl.Optics，1974，13(11):2693-2703.

［3］ 苗二龙，张健，谷勇强，等.用于光刻投影物镜检测的高精度菲佐干涉仪误差分析［J］.中国激光，2010，37(8):2029-2034.MIAO E L，ZHANG J，GU Y Q，et al..Measurement error analysis of high precision Fizeau interferometer for lithography projection objective［J］.Chinese J.Lasers，2010，37(8):2029-2034.(in Chinese)

［4］ 刘兆栋，陈磊，韩志刚，等.斜入射干涉检测大口径碳化硅平面反射镜［J］.光学 精密工程，2011，19(7):1437-1443.LIU ZH D，CHEN L，HAN ZH G，et al..Measurement of large aperture SiC flat mirrors by oblique incidence interferometry［J］.Opt.Precision Eng.，2011，19(7):1437-1433.(in Chinese)

［5］ 吴栋，朱日宏，陈磊，等.抗振型移相干涉仪中PZT移相器的改进［J］.光学 精密工程，2003，11(6):567-571.WU D，ZHU R H，CHEN L，et al..Improvement of PZT phase shifter in vibration-resistant phase-shifting interferometer［J］.Opt.Precision Eng.，2003，11(6):567-571.(in Chinese)

［6］ CHAI L Q，XU Q，YU Y J，et al..500-mm-aperture wavelength-tuning phase-shifting interferometer［J］.SPIE，2005，5956:589-596.

［7］ 杨李茗，叶海仙.大口径大曲率半径光学元件的高精度检测［J］.光学 精密工程，2011，19(6):1207-1212.YANG L M，YE H X.High-precision metrology for optical components with large-apertures and large radii of curvature［J］.Opt.Precision Eng.，2011，19(6):1207-1212.(in Chinese)

［8］ CHENG Y Y，WYANT J C.Phase shifter calibration in phase-shifting interferometry［J］.Appl.Optics，1985，24(18):3049-3052.

［9］ CHIAYU A，WYANT J C.Effect of piezoelectric transducer nonlinearity on phase shift interferometry［J］.Appl.Optics，1987，26(6):1112-1116.

［10］ KENICHI H，BOB F O，KIERAN G L.Phase-shifting algorithms for nonlinear and spatially nonuniform phase shifts［J］.J.Opt.Soc.Am.A，1997，14(4):918-930.

［11］ 王道档，杨甬英，刘东，等.压电移相器的空间旋转误差建模与实验分析［J］.光电子·激光，2009，20(5):571-575.WANG D D，YANG Y Y，LIU D，et al..Modeling and analysis of space-rotation error induced by phase-shifter in phase shifting interferometry［J］.J.Optolectronics Laser，2009，20(5):571-575.(in Chinese)

［12］ 张景和，张顺国，董跃华.乌氏干涉测量的信息读取［J］.中国光学，2011，4(2):147-153.ZHANG J H，ZHANG SH G，DONG Y H.Information reading of Ubbelohde interferometry［J］.Chinese Optics，2011，4(2):147-153.(in Chinese)

［13］ BERND G，HERBERT W.Phase-shifter calibration and error detection in phase-shifting applications:a new method［J］.Appl.Optics，1998，37(32):7624-7631.

［14］ PETER D G.Phase-shift calibration errors in interferometers with spherical Fizeau cavities［J］.Appl.Optics，1995，34(16):2856-2863.