空间激光与单模光纤和光子晶体光纤的耦合效率

陈雪坤，张 璐，吴志勇

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.中国科学院大学，北京100049）

空间激光与单模光纤和光子晶体光纤的耦合效率

陈雪坤1，2，张 璐1，2，吴志勇1*

（1.中国科学院长春光学精密机械与物理研究所，吉林长春130033；2.中国科学院大学，北京100049）

为了设计最优光纤耦合系统，利用高斯模场近似单模阶跃光纤的模场和大模面积光子晶体光纤的模场，推导出了理想情况下空间激光与这两种光纤的耦合效率解析表达式以及光纤端面相对于耦合系统存在横向偏移和端面倾斜时的耦合效率解析表达式。基于上述理论表达式计算了空间激光与光纤的耦合效率，并通过实验验证了此理论表达式的有效性。理论计算和实验均证实了单模阶跃光纤对于横向偏移更敏感，当横向偏移量等于单模光纤的纤芯半径时所对应的耦合效率只有20.25%，为理论最大值的1/4；而大模面积光子晶体光纤对于端面倾斜更加敏感，当端面倾斜2°时对应的耦合效率只有40.5%，为理论最大值的1/2。所提出理论表达式和实验方法完全可以为设计光纤耦合系统提供准确的参数。

单模光纤；光子晶体光纤；空间激光；光纤耦合；耦合效率；横向偏移；端面倾斜

1 引 言

空间光与光纤的耦合技术是激光雷达系统、自由空间光通信系统和恒星干涉仪系统中的关键和难点技术。在这些系统中高效率的空间光耦合是实现高性能系统的前提。空间光与光纤的耦合效率通常受耦合模场不匹配、横向偏移、端面倾斜和系统随机角抖动[1-4]等因素的影响。对于星际自由空间光通信，激光经过几千公里的传输后其光斑有km量级的直径，而接收光学系统的口径不过cm量级（一般不超过20 cm），因此接收的光波完全可近似为平面波。这种情况下研究的耦合问题就是研究模场不匹配、对不准和随机角抖动等因素对耦合效率的影响。

对于自由空间光通信系统，马晶[5]和Toyoshima[6]等人都通过推导得到了在随机角抖动情况下的耦合效率解析表达式，由此研究了系统的随机角抖动对空间激光与单模光纤（SMF）的耦合效率的影响。而在恒星干涉仪系统中，由于光子晶体光纤（PCF）的无截止单模特性[7-9]，使PCF在恒星干涉仪中得到了广泛的应用，并且使用PCF代替传统的单模阶跃光纤（SMF-SIF）成为了一种趋势[10-15]。Corbett等人[11-13]利用数值结合实验的方法研究了恒星干涉仪系统中星光与大模面积光子晶体光纤（LMA-PCF）的耦合效率。而Nahar等人[16]利用光束传输仿真结合实验的方法研究了空间激光与PCF的耦合效率。但由于PCF模场的复杂性，要得到空间激光与PCF耦合效率的解析表达式很困难。

基于已经提出的PCF模场的高斯近似理论[17]，本文推导了理想情况下空间激光与这两种光纤的耦合效率表达式和光纤端面相对于耦合系统存在横向偏移和端面倾斜时的耦合效率表达式。基于此理论表达式研究了空间激光与光纤的耦合效率，并通过实验验证了此理论表达式的有效性。

2 耦合效率模型

2.1 理想情况下的耦合效率

通常自由空间光波到光纤的耦合模型如图1所示。自由空间传播的光波由一组耦合透镜聚焦到光纤端面上，耦合透镜组由一个等效焦距为f，直径为D的薄透镜表示。将口径平面A处的入射光场表示为EA（r），在耦合平面B处对应的聚焦光场表示为EB（r）。假设入射在耦合透镜处的光波为平面波，则经过聚焦后，在耦合平面B上的光场[18]为：

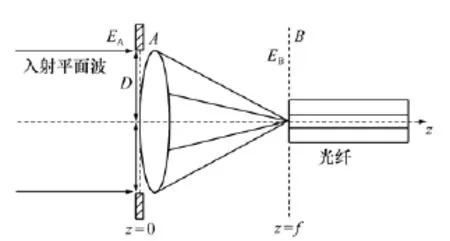
图1 耦合几何模型Fig.1 Mode1 for coup1ing geometry

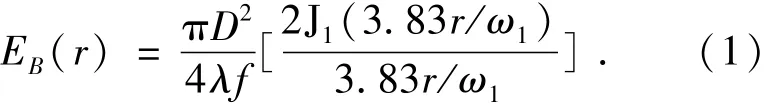
式中：λ是光波波长，J1（·）是零阶第一类贝塞尔函数，ω1=1.22λf/D=1.22λF是爱里斑半径，F是光圈数。

SMF-SIF和PCF的模场都可以用高斯光场进行近似[17]，其中高斯光场对SMF的光场有很高的逼近精度。而对于PCF，高斯光场近似也有很高的近似精度[17]。光纤近似模场为：

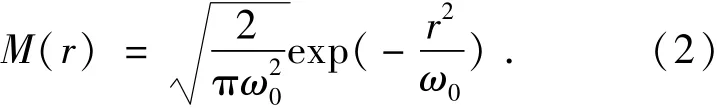
对于此模场表达式有：

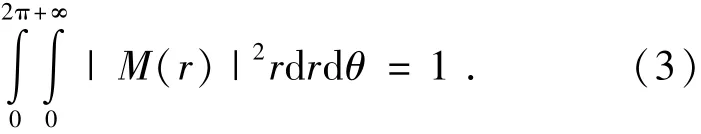
在耦合平面B处，聚焦光场EB（r）到光纤的耦合效率由EB（r）和光纤模场M（r）的重叠积分给出，即为：

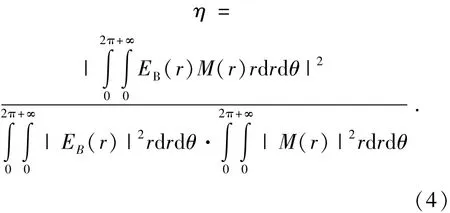
将EB（r）和M（r）的表达式代入上式，可得理想情况下的耦合效率表达式为：

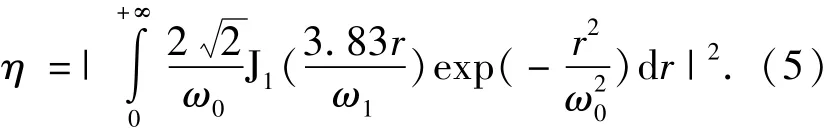
理想情况下的光纤耦合效率忽略了光纤端面引起的菲涅耳反射损耗，该损耗可通过光纤端面镀膜来减小。

2.2 存在横向偏移和端面倾斜时的耦合效率

将光纤模场由极坐标变换为直角坐标可得x=r·cosθ，y=r·sinθ。当光纤相对于耦合透镜光轴存在x方向和y方向上的横向偏移Δx和Δy时，在耦合平面B上的光纤模场变为：

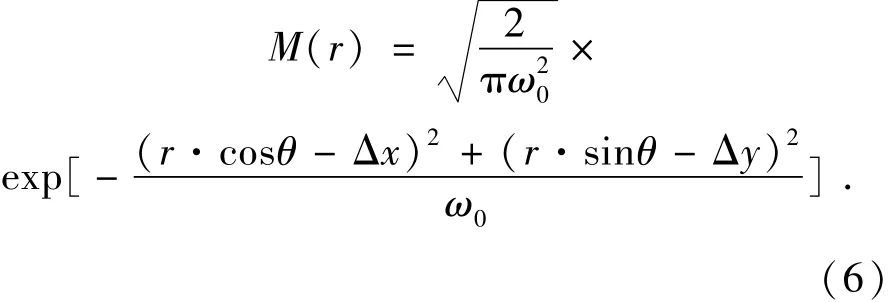
当光纤端面相对耦合系统存在端面倾斜时的耦合几何模型如图2所示。

综上所述，现阶段，我国各大高中学校管理人员已经有效地认知到分层教学模式对于提升学生学习水平的重要性，并且在这种意识的引导下，正在积极开展化学分层教学活动，但是由于起步时间较晚，该种教学模式的教学成效并不显著，因此相关的教职人员必须要将工作重心放到高中化学分层教学模式实施措施的研究上，结合实际情况，制订出具有针对性的措施，以此来实现既定教学目标。

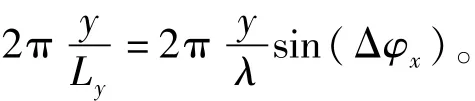
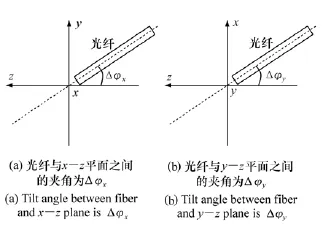
图2 存在端面倾斜时的耦合几何模型Fig.2 Mode1 for coup1ing geometry in the presence of fiber-end ti1t

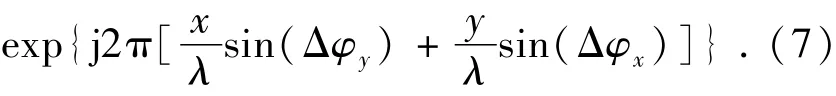
因此，同时存在横向偏移和倾斜时的光纤模场在耦合平面B上的分布为：

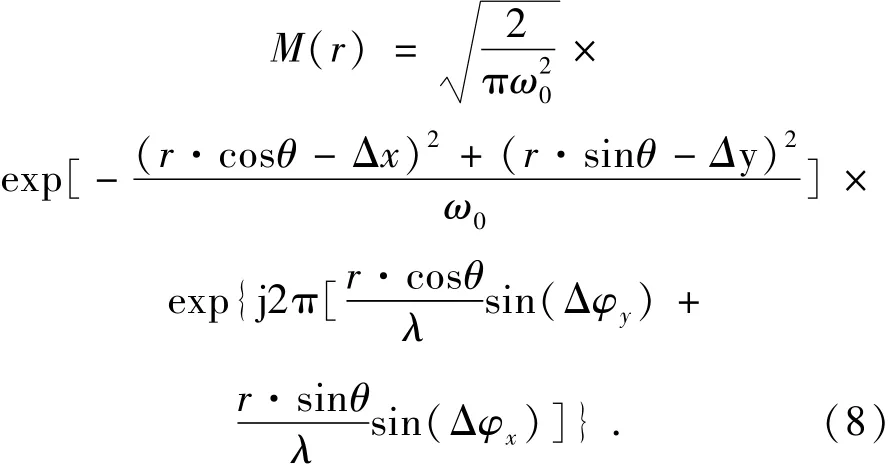
将模场表达式M（r）和聚焦光场表达式EB（r）代入耦合效率公式，可得：

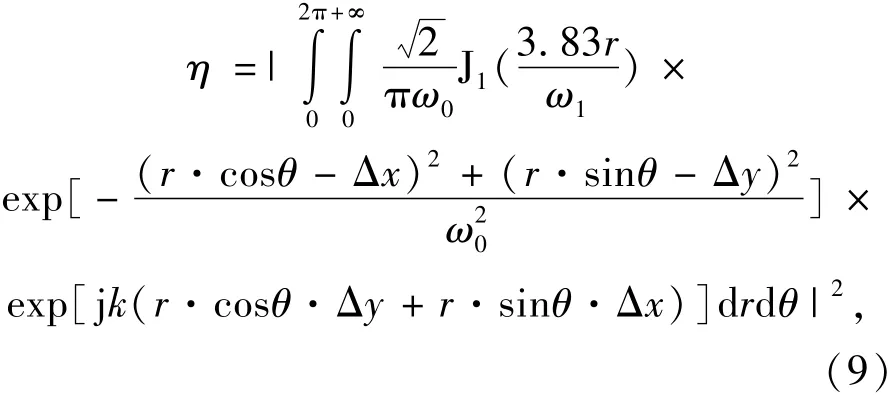
式中：k=2π/λ为波数。当Δx=Δy=0且Δφx= Δφy=0时，可得到理想情况下的耦合效率式（5）。

3 数值结果

SMF-SIF的典型模场半径为ω0=5μm，而LMA-PCF LMA-35的模场半径为ω0=13μm。当入射光波长λ=1.55μm时，由式（5）可得SMFSIF和PCF LMA-35在理想情况下的耦合效率与爱里斑半径之间的关系曲线，如图3所示。

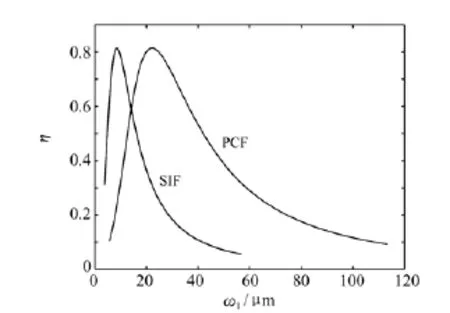
图3 理想情况下耦合效率与爱里斑半径ω1之间的关系Fig.3 Coup1ing efficiency as a function of Airy spot radiusω1in an idea1case

从图3可知，在理想情况下，空间激光到SMF-SIF和到LMA-PCF的理论最大耦合效率都为81.5%。SIF和PCF都对应一个最优爱里斑半径，该最优爱里斑耦合到SIF或PCF时可实现最大耦合效率，这是因为产生最优爱里斑的耦合透镜系统的数值孔径与光纤的数值孔径相比配。但SIF和PCF实现最优耦合时所对应的爱里斑半径却不同。这也意味着SIF实现最优耦合和PCF实现最优耦合需要不同数值孔径的耦合系统。对应图3的SIF和PCF的最优耦合系统如图4所示。

从图4中可知，PCF对应的耦合透镜的数值孔径要比SIF的耦合透镜的数值孔径小得多，这是因为LMA-PCF的数值孔径（NA=0.046）比SIF的数值孔径（NA=0.12）小得多。因此，其对应的最优耦合透镜的焦距就比SIF的最优耦合透镜的焦距长得多。

当光纤端面相对耦合透镜系统仅存在横向偏移Δx或Δy时，Δφx=Δφy=0，而仅存在端面倾斜Δφx或Δφy时，Δx=Δy=0。由式（9）可得归一化耦合效率与横向偏移量和端面倾斜量之间的关系曲线如图5所示。

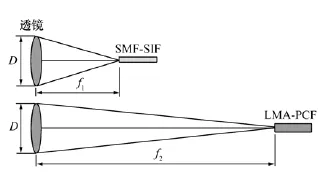
图4 SIF和PCF对应的最优耦合系统示意图Fig.4 Schematic i11ustrations of optimum coup1ing systems for SIF and PCF

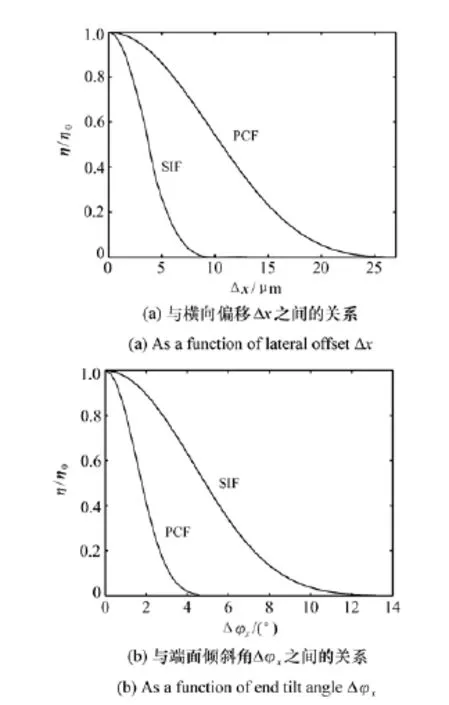
图5 最优光纤耦合效率Fig.5 Optimum fiber coup1ing efficiencies

从图5（a）中可以看出，实现相同的耦合效率时，PCF比SIF可容许存在的横向偏移更大，这是由于LMA-35的模场面积比阶跃SMF的模场面积大得多。因此，精确的横向对准对于SMF-SIF是很重要的。从图5（b）中可以看出，对于实现相同的耦合效率，SIF比PCF可以允许更大的端面倾斜，这是由于SIF的数值孔径比PCF的数值孔径大得多，所以SIF对端面倾斜不敏感。对于PCF，保持端面与耦合平面的平行是最重要的。因此，从图5可以得出结论：SMF-SIF对于横向偏移更敏感，当横向偏移量等于SMF的纤芯半径时所对应的耦合效率只有20.25%，为理论最大值的1/ 4；而LMA-PCF对于端面倾斜更加敏感，当端面倾斜2°时对应的耦合效率只有40.5%，为理论最大值的1/2。

对于PCF，当耦合系统F数变化时，归一化耦合效率与横向偏移和端面倾斜之间的关系如图6所示。

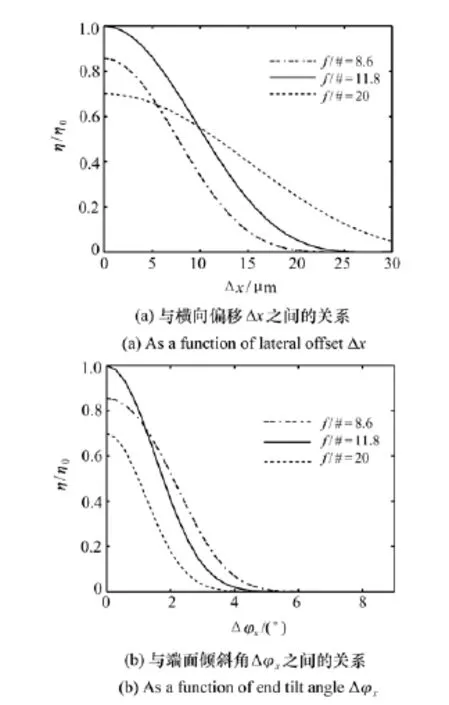
图6 不同F数的耦合系统的归一化光纤耦合效率Fig.6 Norma1ized fiber coup1ing efficiencies for different F numbers

图6（a）中f/#=11.8对应最优耦合系统的F数。从图可知，当横向偏移＞10μm时，f/#=20的次最优耦合系统可以实现更高的耦合效率。因此，可以得出结论：当存在大的横向偏移时，大F数（大于最优耦合系统的F数）的次最优耦合系统可以实现更高的耦合效率。这是由于大F数的耦合系统产生的爱里斑更大，当存在很大的横向偏移时仍然有光斑可以耦合进光纤，而小F数的耦合系统产生的爱里斑小，当横向偏移很大时，整个爱里斑都可能移出了光纤纤芯的区域，所以耦合效率更低。

图6（b）中仍然是f/#=11.8对应最优耦合系统的F数。从图可知，当端面倾斜＞1.8°时，f/#=8.6的次最优耦合系统可以实现更高的耦合效率。因此当端面倾斜相对大时，小F数（小于最优耦合系统的F数）的次最优耦合系统可以实现更高的耦合效率。这是由于小F数的耦合系统的数值孔径更大，当存在较大端面倾斜时，耦合系统的数值孔径对应的立体角范围与LMA-PCF光纤的数值孔径对应的立体角范围仍然有较大重合，而大F数的耦合系统的数值孔径更小，端面倾斜使耦合系统的数值孔径对应的立体角范围与LMA-PCF的数值孔径对应的立体角范围的重合很小，所以耦合效率低。

4 实 验

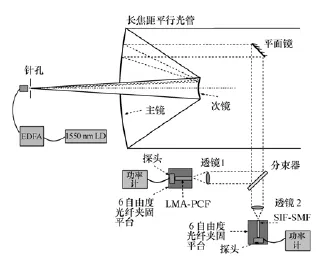
图7 空间激光与单模光纤和光子晶体光纤的耦合效率测量原理图Fig.7 Schematic diagram of coup1ing efficiency measurement for free-space 1aser coup1ing into SIF and PCF

空间激光与SIF-SMF和LMA-PCF的耦合效率测量原理如图7所示。1 550 nm激光器发出的激光经过掺铒光纤放大器（EDFA）放大后由准直透镜组准直后照射在针孔上产生点光源。点光源经过平行光管后变为平面波，由平面镜反射到分束器上，分束器将50%的能量反射后由透镜组1聚焦在LMA-PCF上，由功率计测量耦合前和耦合后的功率。分束器将50%的能量透射后由透镜组2聚焦在SIF-SMF上，同样由功率计测量耦合前和耦合后的功率。测量理想情况下的耦合效率时6自由度光纤夹固平台处于归零状态。当测量横向偏移和端面倾斜时由6自由度光纤夹固平台调节相应偏移量和倾斜量来实现。而通过更换耦合透镜组1和2可以实现不同耦合系统F数下耦合效率的测量。整个光路的调整使用了红外相机对光斑进行了成像。实验中所用器件的参数如表1所示。

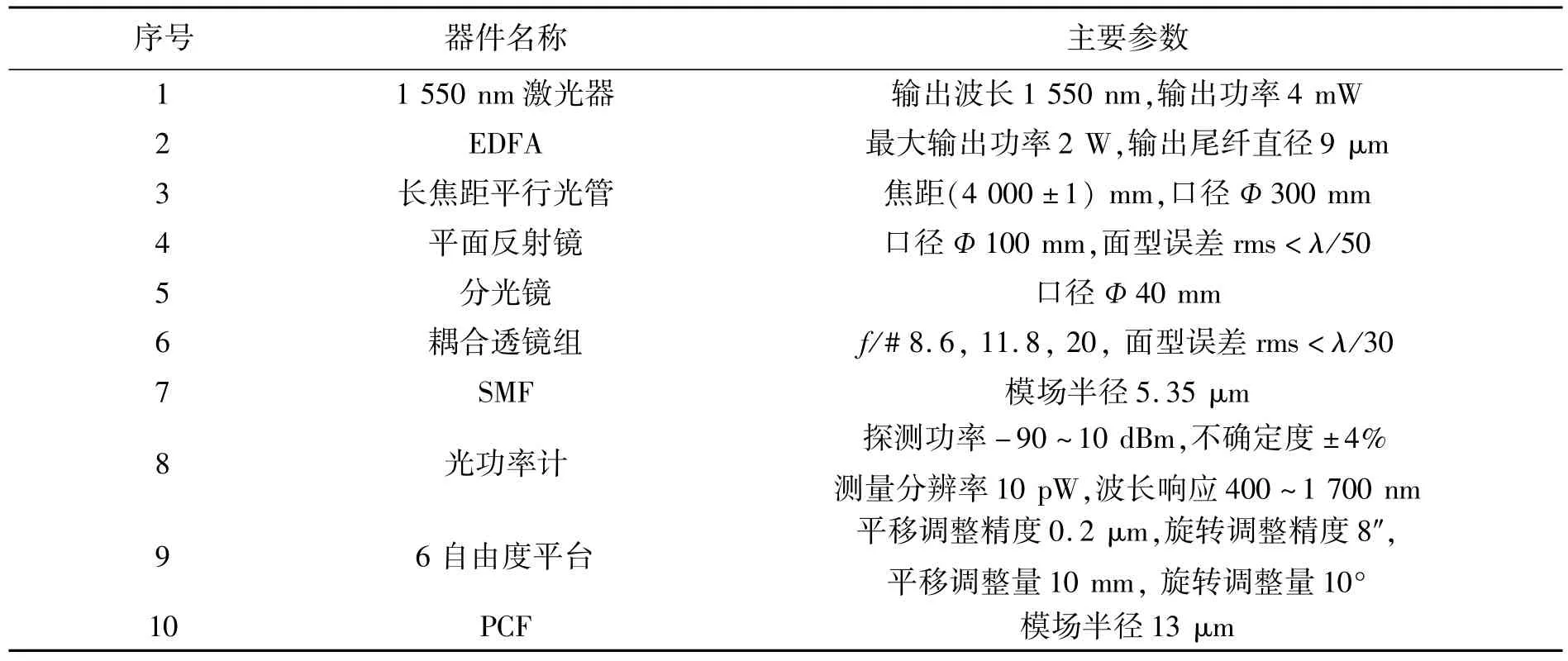
表1 实验所用器件的参数Tab.1 Pamarem ters used in the experiment

图8给出了理想情况下SMF和PCF的耦合效率的测量值和理论值的比较。

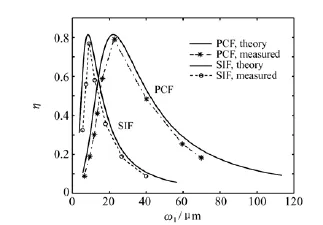
图8 理想情况下理论耦合效率和测量耦合效率与爱里斑半径ω1之间的关系Fig.8 Theoretica1 and measured coup1ing efficiencies as a function of Airy spot radiusω1in an idea1 case

从图8可知，由于实验中所用的SIF-SMF和PCF的端面都没有镀膜，所以实际测量的耦合效率比理论耦合效率要小，实际测量的最大耦合效率只有78%。

图9给出了存在横向偏移和端面倾斜的情况下SMF和PCF的耦合效率的测量值和理论值的比较。从图9可知，SIF-SMF的测量耦合效率由于菲涅耳反射损耗的原因要小于理论计算值，但测量耦合效率曲线的趋势与理论曲线是一致的。对于LMA-PCF，测量耦合效率与理论曲线更接近，但也小于理论计算值。当存在大横向偏移和大角度倾斜时测量耦合效率比理论曲线要大，这是因为理论耦合效率计算使用了高斯模场来近似真实的PCF模场，而实际的LMA-35PCF由于是多孔结构，所以用高斯模场近似产生一定的误差。实际上即使爱理光斑偏移出了PCF的纤芯区域，但仍能照射在孔洞区域，从而仍有光耦合到PCF中，所以测量的耦合效率比理论计算值要大。

由以上实验结果和理论结果的对比可知，理论耦合效率表达式对SMF更适用。因此这里只针对不同的耦合系统，给出空间激光到PCF的理论耦合效率和测量耦合效率与横向偏移和端面倾斜之间的关系，如图10所示。

从图10中可以看出，测量耦合效率的变化趋势与理论计算曲线的变化趋势一致，只是在大横向偏移和大端面倾斜时理论耦合效率偏小。通过实验测量结果和理论结果比较可知：虽然用理论耦合效率表达式计算LMA-PCF的耦合效率存在一定的误差，但是这些误差都在5%左右，而且都发生在大横向偏移和大端面倾斜的情况，因此用理论表达式分析PCF的耦合效率仍然是可行的。

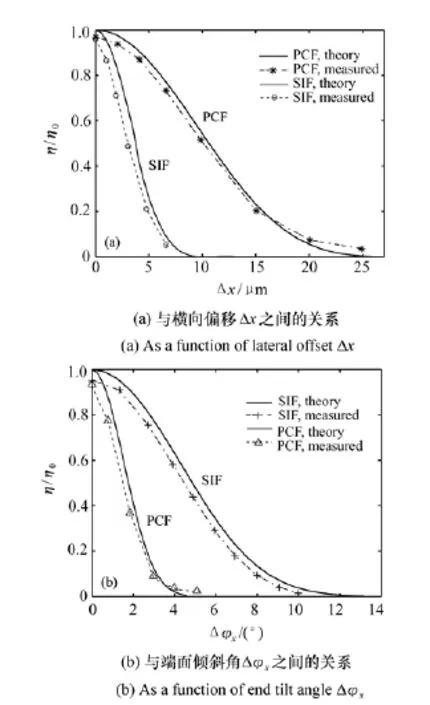
图9 理论的和测量的最优光纤耦合效率Fig.9 Theoretica1 and measured optimum fiber coup1ing efficiencies

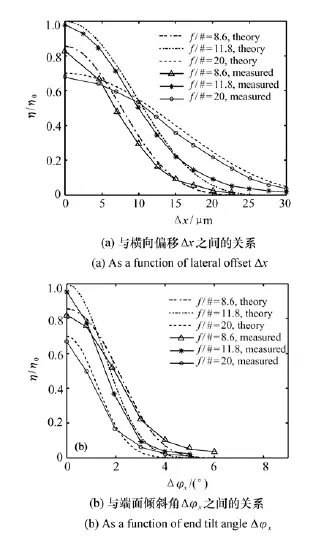
图10 理论上和测量的不同F数耦合系统的归一化光纤耦合效率Fig.10 Theoretica1 and measured fiber coup1ing efficiencies for different F numbers

5 结 论

本文利用高斯模场来近似SIF-SMF的模场和LMA-PCF的模场，从而推导出了理想情况下空间激光与这两种光纤的耦合效率表达式，并得到了光纤端面相对于耦合系统存在横向偏移和端面倾斜时的耦合效率表达式。数值结果和实验结果都表明：所得到的理论表达式准确地描述了耦合效率，并且证明了SMF对于横向偏移较为敏感，当横向偏移量等于SMF的纤芯半径时所对应的耦合效率只有20.25%，为理论最大值的1/4；而PCF对于端面倾斜比较敏感，当端面倾斜2°时对应的耦合效率只有40.5%，为理论最大值的1/2。通过实验可知：对于LMA-PCF，在大横向偏移和大端面倾斜时耦合效率理论表达式具有局限性。同时可以看出要实现理论最优耦合必须考虑菲涅耳反射损耗的影响。因此，本文所得到的耦合效率的解析表达式和耦合效率测量方法完全可以为耦合光学系统的设计提供指导

[1] POLISHUK A，ARNON S.Optimization of a 1aser sate11ite communication system with an optica1preamp1ifier[J].J.Opt. Soc.Am.A，2004，21：1307-1315.

[2] TOYOSHIMA M，JONO T，NAKAGAWA K，etal..Optimum divergence ang1e of a Gaussian beam wave in the presence of random jitter in free-space 1aser communication systems[J].J.Opt.Soc.Am.A，2002，19：567-571.

[3] CHEN CC，GARDNER C S.Impactof random pointing and tracking errors on the design of coherentand incoherentoptica1intersate11ite communication 1inks[J].IEEE Trans.Commun.，1989，37：252-260.

[4] ARNON S，ROTMAN SR，KOPEIKA N S.Performance 1imitations of a free-space optica1communication sate11ite network owing to vibrations：heterodyne detection[J].Appl.Opt.，1998，37：6366-6374.

[5] MA J，ZHAO F，TAN L Y，et al..P1ane wave coup1ing into sing1e-mode fiber in the presence of random angu1ar jitter[J]. Appl.Opt.，2009，48（27）：5184-5189.

[6] TOYOSHIMA M.Maximum fiber coup1ing efficiency and optimum beam size in the presence of random angu1ar jitter for free-space 1aser systems and their app1ications[J].J.Opt.Soc.Am.A，2006，23（9）：2246-2250.

[7] KNIGHT JC，BIRKST A，RUSSELL PSt J，et al..A11-si1ica sing1e-mode optica1 fiberwith photonic crysta1c1adding[J]. Opt.Lett.，1996，21（19）：1547-1549.

[8] LU S，LIW，GUO H，et al..Ana1ysis of birefringent and dispersive properties of photonic crysta1 fibers[J].Appl.Opt.，2011，50（30）：5798-5802.

[9] XIX M.Mode-fie1d expansion in photonic crysta1 fibers[J].Appl.Opt.，2011，50（25）：E50-E54.

[10] RUILIER C，CASSAING F.Coup1ing of 1arge te1escope and sing1e-mode waveguides：app1ication to ste11ar interferometry [J].J.Opt.Soc.Am.A，2001，18（1）：143-149.

[11] CORBETT JCW，ALLINGTON-SMITH JR.Coup1ing star1ight into sing1e-mode photonic crysta1 fiber using a fie1d 1ens [J].Opt.Express，2005，13（17）：6527-6540.

[12] CORBETT J，DABIRIAN A，BUTTERLEY T，et al..The coup1ing performance of photonic crysta1 fibres in fibre ste11ar interferometry[J].Mon.Not.R.Astron.Soc.，2006，368：203-210.

[13] CORBETT JCW，MORRIST J，ALLINGTON-SMITH JR.Tip-ti1t requirements for coup1ing star1ight into sing1e-mode photonic crysta1 fibres using a 1ens1et：a first ana1ysis[J].New Astron.Rev.，2006，49（12）：675-680.

[14] POPPETT C，ALLINGTON-SMITH J.Coup1ing efficiency and termination of photonic crysta1 fibres for astronomy[J]. SPIE，2008，7018：7018Y1.

[15] VERGNOLE S，DELAGE L，REYNAUD F，et al.Using photonic crysta1 fibre in the frame of ste11ar interferometer[J]. SPIE，2004，5491：1416-1424.

[16] NAHAR N K，ROJASR G.Coup1ing 1oss from free space to 1arge mode area photonic crysta1 fibers[J].J.Lightwave Technol.，2008，26（22）：3669-3676.

[17] HIROOKA T，HORIY，NAKAZAWA M.Gaussian and Sech approximations ofmode fie1d profi1es in photonic crysta1 fibers[J].IEEE Photonics Techonol.Lett.，2004，16（4）：1071-1073.

[18] GOODMAN JW.Introduction to Fourier Optics[M].New York：McGraw-Hi11，1996.

Coupling efficiency of free-space laser coupling into singlemode fiber and photonic crystal fiber

CHEN Xue-kun1，2，ZHANG Lu1，2，WU Zhi-yong1*
（1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.University of Chinese Academy of Sciences，Beijing 100049，China）
*Corresponding author，E-mail：ziluit@163.com

It is necessary to confirm the system parameters by theoretica1ana1ysis and experiments for designing a optimum fiber-coup1ing system.By approximating themode fie1ds of a Sing1e Mode Fiber（SMF）with a step index and a Photonic Crysta1Fiber（PCF）with a Large Mode Area（LMA）using the Gaussianmode fie1d，two ana1ytica1expressions for fiber-coup1ing efficiency in an idea1case and in the presences of1atera1offsetand fiber-end ti1t are derived.Based on the two theoretica1expressions，the efficiency for free-space 1aser coup1ing into the fibers is computed.Moreover，the va1idity of the two expressions are verified by experiments.As a resu1t，the theoretica1computation and experiments demonstrate that the SMFwith the step index ismore sensi-tive to the 1atera1offset compared to the PCF.When the offset is equa1 to the radius of the fiber core，the efficiency is on1y 20.25%，which is a quarter of the theoretica1maximum efficiency.Besides，the PCF with the LMA ismore sensitive to the fiber-end ti1t.When the ti1t ang1e is 2°，the efficiency is on1y 40.5%，which is a ha1f of the theoretica1maximum efficiency.In conc1usion，the proposed theoretica1 expressions and experiments can provide accurate parameters for designing fiber-coup1ing systems.

sing1emode fiber；photonic crysta1 fiber；free-space 1aser；optica1 fiber coup1ing；coup1ing efficiency；1atera1offset；end ti1t

TN25；TN249

A

10.3788/CO.20130602.0208

1674-2915（2013）02-0208-08

2012-12-17；

2013-01-23

中科院长春光机所所内创新资助项目（No.Y10532B110）