基于GMRF模型的统计特征畸变织物疵点识别
2013-03-10杨晓波
杨晓波
(浙江财经学院 信息分院,浙江 杭州 310012)
统计特征畸变是指疵点区域的统计纹理特征与标准织物产生了较大的差异,如松经、跳花、云织等。它们一般采用统计纹理分析方法来进行自动检测,其中采用纹理模型来分析图像的统计纹理特征是纹理分析的有效方法之一。
在纹理分析中引入纹理模型的最大优点在于:纹理模型能够从统计的角度,通过其模型参数高效地表示任意一幅图像信息。随机场纹理模型是一类重要的纹理模型,它在图像处理和分析中应用非常广泛[1]。目前较为流行的随机场纹理模型有2类:一类为 ARMA纹理模型[2],另一类为Markov随机场(MRF)纹理模型,由于后者模型要求的Markov性更符合自然纹理的一般约束特性,因而在许多场合中MRF纹理模型更适用于纹理图像的建模和分析。作为一种有力的统计纹理图像分析工具,MRF纹理模型在图像分析和计算机视觉中得到了成功的应用,如纹理合成[3-4]、图像分割[5]、边缘检测[6]、纹理分类[7]、图像恢复[8]和运动图像分析[9]等。
应用MRF纹理模型时,一般均假设模型的激励噪声服从 Gaussian分布,因而该模型又称为Gaussion-Markov随机场(GMRF)模型,本文将重点讨论基于GMRF纹理模型的统计特征畸变的织物疵点自动检测方法。
1 GMRF模型的纹理合成
GMRF模型及其应用主要有2个分支[10],应用时涉及到2大重要问题:参数估计和最佳邻域集选取。常用的GMRF模型参数估计和最佳邻域集方法有:最大似然估计[11]、最小二乘估计[12]、基于编码技术的估计[13]、EM 算法[14]。
GMRF模型的纹理合成关键在于能生成零均值平稳Gaussian噪声序列{e(s)},s=(i,j)∈Ω。其中s为图像序列,Ω为图像两维格,(i,j)表示在图像水平和垂直方向的取值变量。为此首先计算随机序列 {vi,j}。
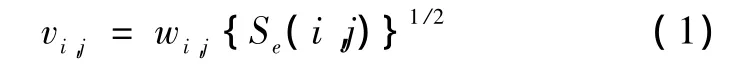
式中:
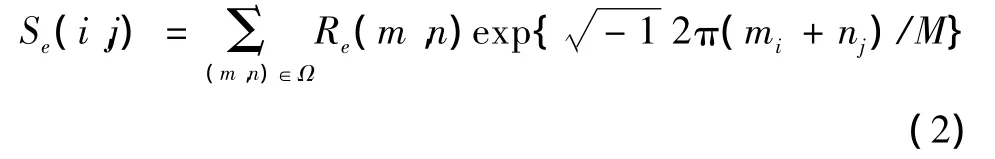
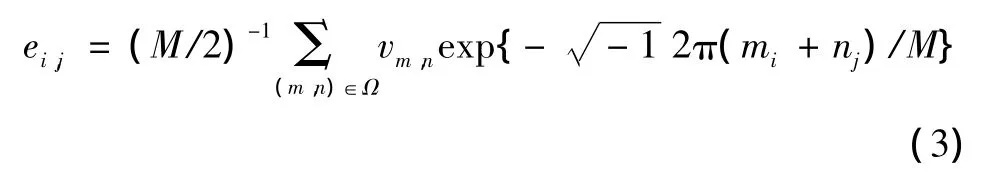
ei,j为水平和垂直方向的零均值平稳 Gaussian噪声序列。
表示成矩阵向量形式,可得:

式中,Y为模拟纹理图像,F表示 Fourier变换。式(1)、(3)、(4)给出了满足 GMRF模型的纹理合成算法,其步骤为:
1)生成独立等分布Gaussian噪声序列{ws};
2)根据式(1)生成噪声序列{vs};
3)根据式(3)生成相关 Gaussian噪声序列{e(s)};
4)计算对称块循环矩阵的特征值{λs};
The basic form of a transformer based matching network (TMN) is shown in Fig. 1, which consists of two parallel RLC tanks in the primary and secondary sides respectively, and a coupling coefficient k between them.
5)计算相关 Gaussian噪声序列{e(s)}的Fourier变换 Ê,将 Ê与{λs}对应元素相除后,对该结果进行Fourier反变换,如式(4)所示,所得结果Y便为满足给定GMRF模型的计算机模拟纹理图像。
2 GMRF纹理模型的仿真实验
为了验证上述GMRF模型参数估计算法和纹理合成算法的正确性,设计了仿真实验。实验步骤是:首先根据给定的 GMRF模型参数通过上述纹理合成算法生成模拟纹理图像;然后再通过上述模型参数估计方法计算该模拟纹理图像GMRF模型参数的最大似然估计;最后比较这2组参数是否相符,若相符则说明上述2种算法,即GMRF模型参数估计算法和纹理合成算法是正确的。
采用上述步骤模拟GMRF纹理图像,图像大小为128像素 ×128像素,仿真实验的结果如图1所示。

图1 计算机模拟GMRF纹理图像Fig.1 Computer simulation GMRF texture images.(a)Two rank GMRF computer simulation texture image;(b)Four rank GMRF computer simulation texture image
采用二阶和四阶GMRF模型生成的模拟纹理的实验参数对比结果见表1。
从参数对比可以看出,真实模型参数与它的最大似然估计非常接近。对于值原本较大的参数,其估计误差较小;而对于值原本较小的参数,其估计误差较大。最大似然估计的精度受到被估计图像样本大小的影响,图像样本越大,则最大似然估计越接近真实模型参数,一般图像样本取64像素 ×64像素便可以满足精度要求。

表1 不同阶数GMRF模型参数对比Tab.1 Parameters comparison of GMRF model of different ranks
3 GMRF模型的织物疵点检测
3.1 织物疵点的检测流程
利用GMRF模型进行织物纹理建模时,正常织物纹理的GMRF模型参数是固定的,若织物出现统计特征畸变时,则其模型参数必然会发生变化。通过检测这种参数的变化,可用于判别织物表面是否存在发生统计特征畸变的疵点。疵点检测可以基于Bayes准则或其他标准分类准则,如最小距离准则等,实践表明,采用似然比检验的Bayes分类方法对织物疵点检测较为理想。
统计特征畸变的织物疵点可以看作2种具有不同统计纹理特征织物的组合,其中一种为正常纹理,即标准织物,另一种为异常纹理即统计特征畸变疵点。对这类疵点的检测主要通过式(5)所示的距离统计量来判断。
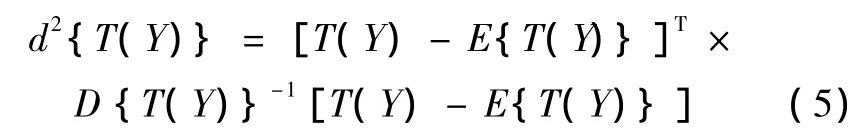
式中:d2{T(Y)}为距离统计量,T(Y)为充分统计量,E{T(Y)}为充分统计量的期望值,D{T(Y)}为充分统计量的方差。当距离统计量大于一定的阈值时,认为布面发生了统计特征畸变。因此,理想状况下,正常织物的距离统计量值较小且离散度也较小,而异常织物的距离统计量则远远大于正常织物,这样才能通过简单的阈值化完成对该类疵点的准确评价。疵点检测的流程如图2所示。
3.2 实际疵布的自动检测
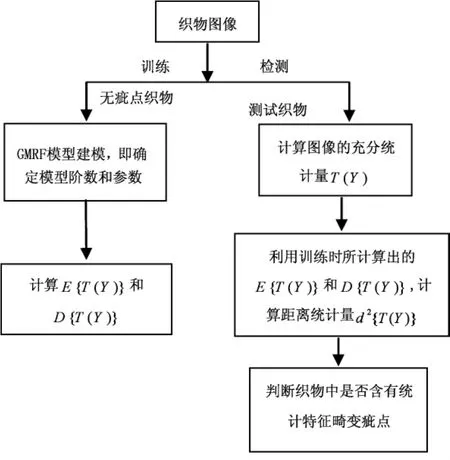
图2 基于GMRF模型的织物疵点自动检测流程Fig.2 Fabric defect automatic detection process based on GMRF model
实验中,可将基于GMRF模型的疵点检测方法应用于实际疵布的检测中,即考察距离统计量对标准织物和疵点的输出对应。标准织物如图3(a)所示,图像大小为128像素×128像素。首先根据图2的疵点检测流程图对标准织物进行训练,即确定它的GMRF模型的阶数和参数,并根据模型参数计算出E{T(Y)}和D{T(Y)}。根据GMRF模型阶数的参数确定方法,表明五阶GMRF模型比较适合标准织物的建模,图3(b)示出了标准织物的五阶GMRF模型仿真织物纹理图像,模型参数见表2。

图3 真实织物及其仿真织物Fig.3 Real fabric and its simulation fabric.(a)Real twill fabric texture;(b)Five rank GMRF simulation fabric texture

表2 五阶GMRF模型参数Tab.2 Five rank GMRF model parameters
确定了模型的参数和阶数后,便可方便地计算出E{T(Y)}和D{T(Y)}。实际检测时,将待检织物划分为32像素×32像素的检测窗口,分别计算各检测窗口内的距离统计量。表3和表4分别列出了图4(a)和图5(a)所示的跳花和稀密路疵布样本中各检测窗口的距离统计量输出,选取适当的阈值(对应于χ2分布的分位数),便可判断各检测窗口是否含有疵点,评判结果如图4(b)和图5(b)所示。
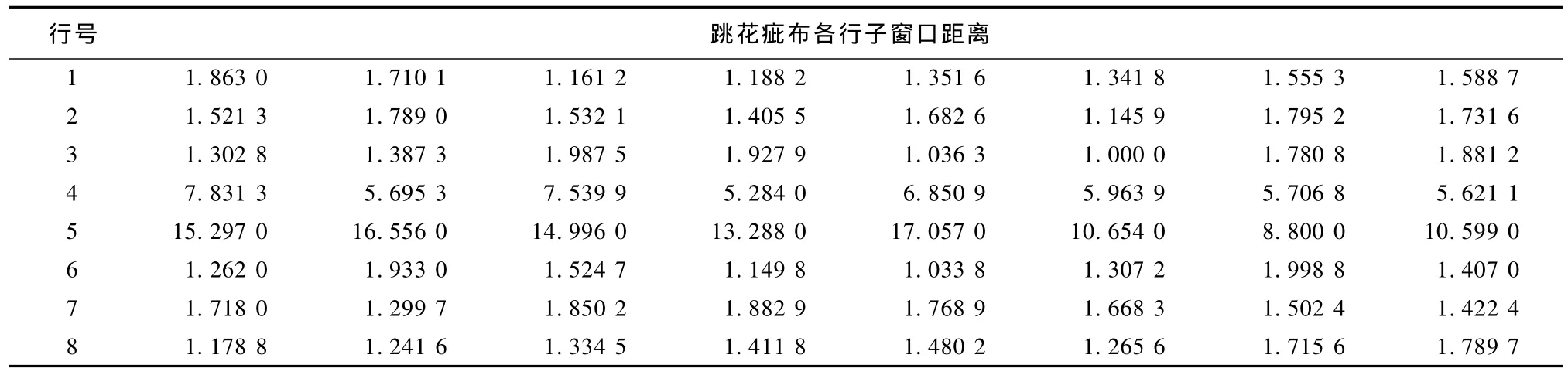
表3 跳花疵布样本图像各子窗口距离Tab.3 Each sub-window distance of jump defect fabric sample image
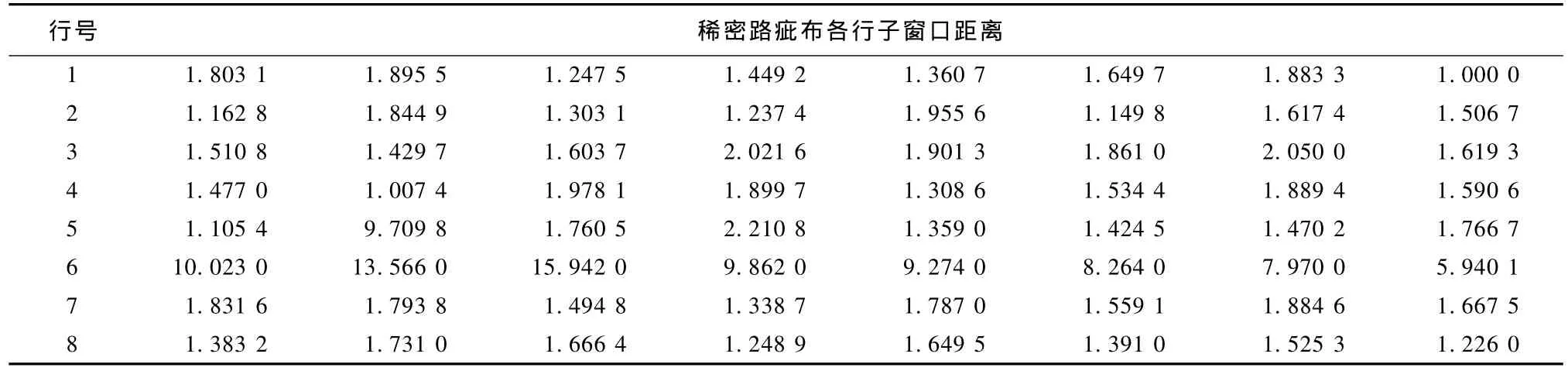
表4 稀密路疵布样本图像各子窗口距离Tab.4 Each sub-window distance of weft crackiness defect fabric sample image

图4 跳花疵点检测Fig.4 Floating defect detection.(a)Floating defect sample;(b)Detection result
阈值的选取很重要,较大的阈值会引起误检;而较小的阈值则会导致漏检。跳花和稀密路疵点均属于本文所定义的统计特征畸变疵点种类,它们均会引起检测窗口距离统计量相对于正常织物发生较大的畸变。实验证明,基于GMRF模型构造的距离统计量能够非常敏感地检测出织物表面存在的统计畸变疵点,而对于断纱、粗纱和细小杂质等疵点区域面积相对较小的疵点,距离统计量的敏感性将受到明显削弱,尤其是当检测窗口面积较大时,其效果更差;对于有些细小的杂质,GMRF模型甚至会将它们归结为散弹噪声,而不会使GMRF模型参数发生任何变化。

图5 稀密路疵点检测Fig.5 Weft density defect detection.(a)Weft density defect sample;(b)Detection result
在实验过程中发现:所选窗口越大时,正常窗口距离统计量值之间的波动变小,但疵点窗口和正常窗口之间的距离差异也变小。前种趋势有利于疵点检测,而后者却不利于疵点检测,因此在选择窗口大小时,应充分考虑这2种趋势。另外,允许检测窗口产生一定量的重叠将有利于疵点的准确检出。
图4中需要说明的是,所选图像大小为256像素×256像素,子窗口大小为32像素×32像素,阈值为5,“D“表示有疵点,“ND”表示无疵点。
从表3可以得出,跳花疵点出现在图像的第4行和第5行,此处所对应的子窗口距离统计量也较大,与检测结果相一致。
图5中所选图像大小为256像素 ×256像素,子窗口大小为32像素×32像素,阈值为5,“D”表示有疵点,“ND”表示无疵点。
从表4可以得出,稀密路疵点出现在图像的第6行,此处所对应的子窗口距离统计量比其他行都大,说明有疵点出现,与检测结果相一致。
本文还选取了其他2类统计特征畸变织物疵点(粗纱疵点、断经疵点)进行验证,同样得到类似的检测结果,在此不一一赘述。另外,不同的疵点种类对应的疵点位置不同,依据不同的疵点位置就能确定不同的疵点种类。
实际检测中所采用的硬件环境为 Dell620,512 M内存的微型计算机,软件环境为MatLab6.0。对于1幅大小为512像素×512像素的待检织物图像,整个检测过程(不包含对织物进行建模)需耗时1.81 s,假若织物纬密为100根/10cm,且CCD不沿纬向移动,同时假设图像采样分辨率为0.5 mm/pixel,则该算法能够达到的最高检测速度为8 m/min。
4 结论
本文研究了GMRF模型的参数估计和多种织物的GMRF建模方法,并针对统计特征畸变疵点,研究了基于GMRF模型的疵点自动检测方法,从中可以得出以下结论。
1)GMRF模型是随机场模型中比较适合于织物纹理建模的一类模型,它能够通过其模型参数简洁地表示多种织物。GMRF仿真织物与其对应的实际织物在视觉效果上非常相似。
2)正常织物的GMRF模型参数在恒定的图像分辨率下是不变的,但当织物中出现统计特征畸变
3)基于GMRF模型的织物疵点自动检测过程可分为训练阶段和实时阶段。训练阶段完成对正常织物 GMRF模型建模,并估计正常织物GMRF模型参数;实时阶段则根据训练阶段所得正常织物的GMRF模型参数和待检织物GMRF模型参数的充分统计量,计算距离统计量,根据该距离统计量值的大小判断待检织物中是否含有统计特征畸变疵点。
4)基于GMRF模型的织物疵点方法适用于统计特征畸变疵点的自动检测。通过GMRF模型参数构造的距离统计量能够敏感地区分正常织物纹理和统计特征畸变疵点纹理。
5)对于区域面积相对较小的疵点,或类似散弹噪声的杂质,该方法的检测效果不佳。
[1]GEORGE R C. Markov random field texture models[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1983,5(2):25-39.
[2]KASHVAP R L.Characterization and estimation of two dimensional ARMA models[J].IEEE Transaction on Information Theory,1984,30(5):736-745.
[3]ONURAL L. Generating connected textured fractal patternsusing Markov random fields[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence,1991,13(8):819-824.
[4]NODA H, SHIRAZIM N, NOGAWAT, etal.Unsupervised Segmentation of Multispectral Images Using Hierarchial MRF Model[M].Englewood Cliffs,NJ:Prentice-Hall,1996.
[5]MANJUNATH BS,CHELLAPPAR. Unsupervised texture segmentation using Markov random fields models[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1991,13(5):478-482.
[6]COHEN F S,FAN Z,PATEL M A.Classification of rotated and scaled textured image using gaussianian Markov random field models[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1991,13(2):192-202.
[7]SPEIS A,HEALEY G.Feature extraction for texture discrimination via random field models with random spatial interaction[J].IEEE Transactions on Image Processing,1996,5(4):635-644.
[8]ZHANG J.The mean field theory in EM procedures for blind Markov random field omage restoration[J].IEEE疵点时,其GMRF模型参数必然发生变化,通过检测这种变化,可完成对织物统计特征畸变疵点的在线检测。Transactions on Image Processing,1993,2(1):27-40.
[9]HEITZ F,BOUTHEMY P.Multimodal estimation of discontinuous optical flow using Markov random fields[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence,1993,15(12):1217-1232.
[10]ELFADEL I M,PICARD R W.Gibbs random fields,cooccurrences, and texture modeling[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence,1994,16(1):24-37.
[11]BALRAM N,MOURA J M F. Noncausal gaussian markov random fields:parameter structure and estimation[J].IEEE Transactions on Information Theory,1993,39(4):1333-1355.
[12]KASHVA R,CHELLAPA R.Estimation and choice of neighbors in spatial interaction models of image[J].IEEE Transaction on Information Theory,1983,29(3):61-72.
[13]BESAG J E.Spatial interaction and statistical analysis of lattice systems[J].J Roy Stat,Soc,Series B,1974,B(36):192-236.
[14]ZHANG J, MONDESTINO W, LANGAN D A.Maximum-likelihood parameter estimation for unsupervised stochasticmodel-based image segmentation[J]. IEEE Transactions on Image Processing,1994,3(4):404-418.
