基于遗传算法的地铁列车自动驾驶控制算法研究

（浙江大学生物医学工程与仪器科学学院 杭州 310027）

0 引 言

轨道交通列车的运行要实现自动化，对列车的运行曲线进行控制是其核心技术．目前普遍使用的列车自动运行解决方案是列车自动控制系统（automatic train control，ATC），一般包括：列车自动监控系统（automatic train supervision，ATS）、列车自动防护系统（automatic train protection，ATP）及列车自动驾驶系统（automatic train operation，ATO）．其中ATO系统主要用于实现“地对车控制”，即通过地面信息实现对列车驱动、制动的控制，使用ATO系统能避免不必要的剧烈加速或减速，可明显提高旅客舒适度和列车的准点率，还可减少列车器件损耗［1－2］．

M．Dominguez［3］提出的 ATO 速度曲线设计法中同样指出，ATO对固定线路条件和关键点能够生成速度曲线解绝对不唯一，但限制条件中运行时间与能耗形成制约关系，将不同曲线的时间－能耗关系作图，可以求出一组帕累托最优曲线集，该组曲线便可以作为最优曲线解集，再结合具体运行限制设计生成不同级别的运行目标曲线，供运行时选择［4］．另一种时分控制方式则以ATP系统为主导，在给出ATO目标曲线后，运行时的时分管理方式不以修改目标曲线为主，而是ATP系统在列车时分状况与目标偏差较大时，通过调整停站时间，在时间富余时手动使用惰行模式或者修改调度表等方法来控制列车时分正点．但在客流高峰时，根据列车情况变动停站时间会对列车的运营载客产生不好的影响，未经预估地使用惰性模式，也可能降低乘客的乘坐舒适性，在机动、效率和经济性上都不好．

以智能算法为核心的ATO通常不依靠固定的目标曲线进行控制，而在ATO车载设备上根据列车环境实时地做出决策，系统中时分控制功能以算法中的关于准点、能耗等要求的具体规则来实现．然而在具体线路上，采用固定的控制规则可能会造成与参数不断变化的实际情况不符；且在控制策略模式方面还有待于对人类控制策略进行深入研究，才能保证算法规则的完善．

1 遗传运行时分控制算法

1.1 ATO运行时分控制的建模

ATO运行时分控制优化生成曲线的功能可分为2类：预先的全段控制曲线生成与运行中的曲线调整（再生成）．前者是离线的曲线生成，其固定两站间初始速度为0；后者是在线的实时调整，用于列车运行中，各种原因造成与初始曲线不匹配时重新生成可行的控制曲线．从算法的角度来说，前者与后者的区别只是初速度是否为零与运行路程长度的区别而已，因此可以用共同的模型解决．

列车运行环境中线路长为1 000m，加速度由－1 000～1 000的控制量决定（该量决定列车的动力输出，但本身只是操作参数，故无单位）由于工作中的精细控制可以通过工况点的位置变化实现，为方便搜索同时考虑与工况符合，将动力控制量分为16个档位．见表1．

表1 动力控制档位

表1中加速度是理论值，未减去各种损耗．其中，前7个档位是制动工况，第8档是惰行工况，后8个档位是牵引工况．高加速度制动会使乘客受到巨大冲击，因此在制动档位设定的最大制动取－840，低于－1 000的最大值动力控制量，以提高舒适度．

本优化算法中设定10个工况点，每个工况点对应于一个站间位置（第10点固定于1 000m处）和相应的动力输出档位如图2所示，x轴为S值，y轴为动力控制量．如图1所示．

图1 动力控制量－路程曲线

以这10个工况点（共20个数据）作为全路段的控制序列，将这个序列代入仿真计算得到全路段的速度、时间、能耗等信息．

解决ATO运行时分问题要满足其多目标性，具体包括：（1）精准停车．根据通行标准，要求列车在已设定站点的停车误差在±25cm范围内以保证列车在站点内与上下车闸门配合；（2）时间准点．要求算法提供的控制方法能保证走行时间与规定值的误差不大于5%；（3）速度防护．给定算法相应路段的最低限速曲线，在搜索曲线时要求能满足限速要求，不超过给定速度的5%；（4）舒适性．为保证乘客乘坐的舒适性，列车加减速度的绝对值不能过大，加减速度的变化不能过于频繁；（5）节能．列车在行驶途中要求以尽量低的速度运行并尽量减少制动，在停靠站点时会考虑牵引力、阻力等因素，自动调整速度以达到节能环保的目标．本研究中，遗传算法的适应度函数就依据前述目标设计来制定．

1.2 遗传算法设计［4－11］

1．2．1 编码

根据本研究问题模型，分别用10位和4位（29＜1 000＜210，16＝24）格雷码编码工况点的路程值与输出值，并将二者级联在一个染色体中，一个工况点有14位基因，模型中共有10个这样的工况点，进一步级联得到一个由140位基因串组成的染色体．编码与解码流程如图2．

图2 编／解码函数流程

1．2．2 适应度函数设定

适应度函数的选择直接影响到遗传算法的收敛速度以及求解性能．本问题的目标函数是最小化问题，需要同时考虑多个适应度变量的协同，且保证各个适应函数在尺度上一致．分别计算各个变量的标准化函数，再综合求出适应度函数为

式中：Fstop为定点停车适应度函数；FSR为限速适应度函数；Fenergy为能耗适应度函数；Fcozy为舒适度适应度函数；Ftime为时间适应度；α，β，γ，δ，ε分别为各函数权重．

式中：Se为实际停车位置；So为目标停车位置；Ss为容许误差，取为0．25m．

式中：vI，vRi分别为工况点i处的速度与限速．

式中：a和b的取值调整指数函数的增长速度，取经验值a＝1．2，b＝0．2．Lcozy是加速度超过额定加速度时的变化率求和，计算方法为为

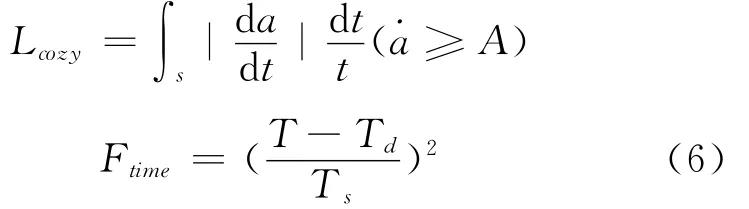
在定时模式下，应以保证限速、定点、舒适度3个性能指标为前提，最大限度满足给定时间要求，较小考虑能耗要求．取值方法：将Td取为目标时间，并将Ftime权重系数ε取为100 000．

最优模式各权重系数均取为1．

1．2．3 惩罚因子

在列车时分曲线生成问题中一些不能用适应度函数来消除的意外情况和限制条件，用特殊的惩罚因子来调整其最终适应度．用到的惩罚因子为

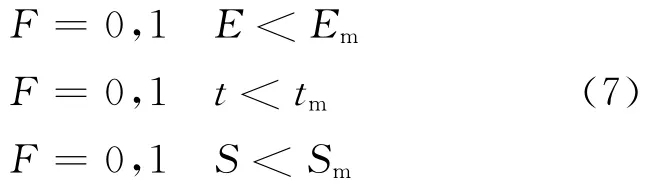
式中3个惩罚因子都是致死因子．在来自随机计算的初始种群中会时常出现途中减速停车、甚至在起点便减速停车，这种现象会严重干扰有效解的搜索，需要及时清除．Em，tm，Sm等参量的取值依据来自该路段最小完成量．虽然致死因子能绝对排除破坏约束条件的个体，但约束过于严格时交叉算子和变异算子在搜索空间中生成新个体的能力就比较差［12］，所以将3个值的阈限在最小完成量的基础上进一步降低，分别取为Em＝1 000，tm＝1 000，Sm＝500．

1．2．4 选择算法

遗传算法使用选择算子来对群体中的个体进行优胜劣汰操作，采用比例选择法即赌盘法来实现．

式中：f（bi）为个体bi的适应度，赌盘法基于随机操作，根据概率有放回地选择M个个体放入作为下一代群体［13］．

1．2．5 交叉算子

在遗传算法中也使用交叉来产生新的个体．进行交叉首先要配对，常用的方法是随机配对，即把M个个体随机组成M／2对，在每对内部进行交叉操作．本研究采用随机配对下的单点交叉．这种方法不会对个体造成较大的模式伤害．

1．2．6 变异算子

直接采用简单变异算子，其实现机理为：以变异概率Pm随机指定某一位或几位基因座上的基因值取反，即把1变成0，把0变成1．

变异概率是针对个体的某个基因座执行的，因此对整个群体来说，变异概率的意义为

式中：B为每代中变异的基因数目；λ为个体基因串总长度．

1．2．7 种群设定

遗传算法是对群体进行操作的，所以必须为遗传操作预先生成一个初始解群体，设定主要包括以下两方面：初始种群生成、种群规模确定．将种群规模设定为25，初始种群在基因串上均匀地随机生成0－1 2个值来形成．

1．2．8 终止迭代次数

终止代数T是表示遗传算法运行结束条件的参数，程序运行到指定代数时停止运行，并输出当前群体中最佳个体作为最优解．一般取值为100～1 000之间，根据实验，通常在500代左右即可得到足够好的个体，故本研究将T值设定为500．

2 程序整体流程图

本研究使用某城市地铁列车参数用于仿真模型．根据输入的动力控制量和步进的前一刻速度、加速度值输出当前速度、加速度及路程值，得到每一步（50ms）下的速度、路程与加速度值．程序整体流程图如图3所示．

图3 程序整体流程图

3 仿真实验

首先求出在最节时模式下列车的运行输出．当最大加速0～576m，最大减速576～1 000m取值时，输出为：运行时间t＝1 336×50ms，停车位置为S＝1 000．28m，能耗E＝394 670kJ；最高速度v＝91．28km／h．

经多次测试迭代次数、变异概率、交叉概率、种群大小等遗传算法运行参数后，能较快得到最高适应度的运行参数为：种群大小为25，交叉概率为0．65，变异概率为0．01．

以最节时模式作为参考做出以下仿真．

1）仅末段路程限速的定时模式搜索 给定条件为：限速0～900m，70km／h；900～1 000m，40km／h．定时要求2 000s．实验得到的适应度－迭代次数图像如4图所示，实验结果输出档位图见图5，v－T 曲线见图6，v－S 曲线见图7．

图4 适应度－迭代次数图像

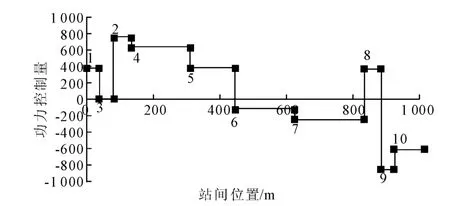
图5 实验结果输出档位图

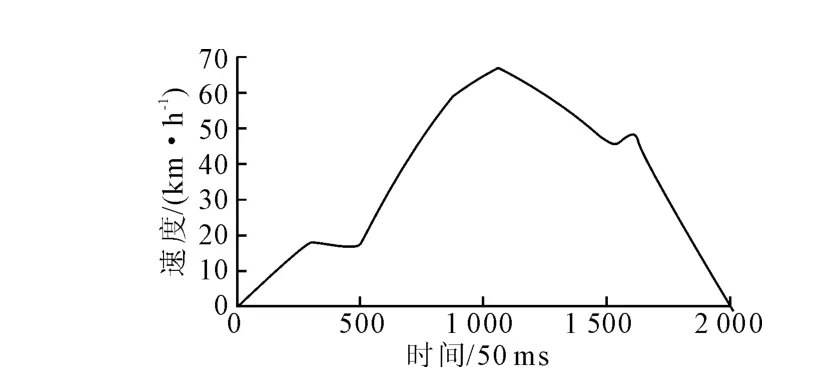
图6 仿真v－T（速度－时间）曲线

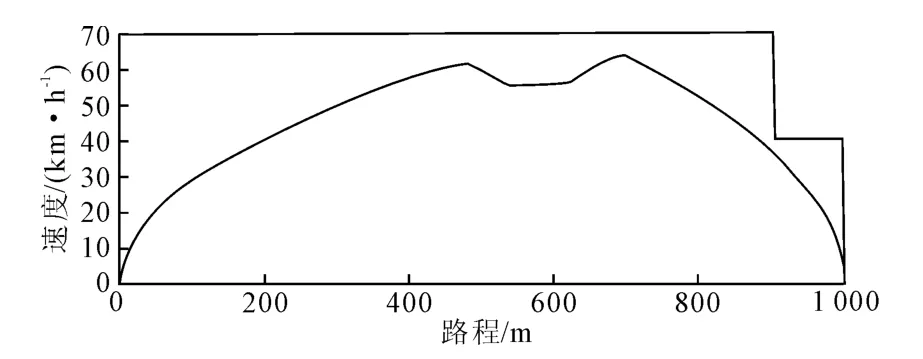
图7 v－S（速度－路程）曲线与对应限速

如图5所示，列车初期保持较低的适应度，在73代时适应度突破了1 000，并迅速上升到6 000以上，此后基本维持不变，因此将最大迭代次数设为500应该能够满足优化目标的精度要求．

其输出时间为2 000×50ms比节时模式慢664×50ms，与给定的定时值2 000×50ms完全一致；能耗为22 011kJ，比节时模式节能44%；停车点为999．86m，精度14cm，小于规定的25 cm；最大速度小于规定的70km／h；适应度函数值为6 469．

如图6，得到的曲线在1 600s时存在一个尖峰，这种情况对乘客的舒适度有比较大的影响，这是因为该次实验使用的舒适度适应度函数不能有效甄别大的加速度变化．另一方面，考虑到遗传算法的全局搜索特性，在定时状态时间与速度限制等要求较死的前提下，适应度函数的效应也许不能得到足够的表达．

2）带有途中限速降低的定时模式搜索 给定条件为：限速0～400m，60km／h；400～500 m，40km／h；500～900m，70km／h；900～1 000 m，30km／h．定时要求2 500s．输出 V－S曲线如图8所示．

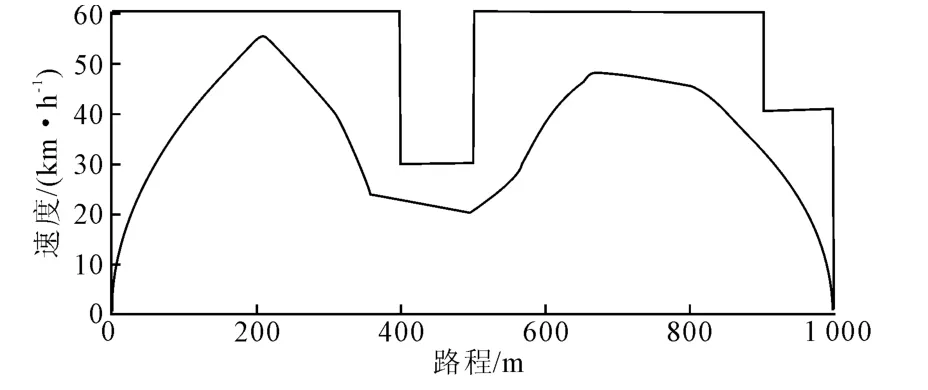
图8 输出v－S（速度－路程）曲线

其输出时间为2 490×50ms，停车精度25 cm，能耗22 092．417kJ．各方面的精度可以满足技术要求．

4 结束语

基于遗传算法对城市轨道交通ATO运行时分控制策略进行仿真有较高的全局适应度．算法效果良好，仿真过程中能较快得到最高适应度的运行参数为：种群大小25，交叉概率0．65，变异概率0．01．

仅末段路程限速的定时模式搜索仿真，输出时间为2 000×50ms比节时模式慢664×50ms，与给定定时值2 000×50ms完全一致；能耗为22 011 kJ，比节时模式节能44%；停车点为999．86m，精度14cm，小于规定的25cm；最大速度小于规定的70km／h；适应度函数值为6 469．

在带有途中限速降低的定时模式搜索下的仿真中，得到的曲线不尽完美，表明本方法在舒适度函数的设计上还有改进的空间．

［1］唐 涛，黄良骥．列车自动驾驶系统控制算法综述［J］．铁道学报，2003，25（2）：98－102．

［2］周家猷，唐 涛．列车自动驾驶系统算法研究［J］．中国科技信息，2008（13）：306－307．

［3］DOMINGUEZ M．Optimal design of metro automatic train operation speed profiles for reducing energy consumptionJ．Journal of Rail and Rapid Transit 2011，225：463－470．

［4］王 艳，曾建朝．多目标微粒群算法综述．智能决策学报［J］．2010，10（5）：377－384．

［5］周 明，孙树栋．遗传算法原理及应用［M］．北京：国防工业出版社，1999．

［6］周 明，孙树栋．遗传算法原理及应用［M］．北京：国防工业出版社，1999．

［7］CHANG C S，SIM S S．Optimising train movements through coast control using genetic algorithms［DB／J］．IEE Proceedings online no，19970797．

［8］周 明，孙树栋．遗传算法原理及应用［M］．北京：国防工业出版社，1999．

［9］周 明，孙树栋．遗传算法原理及应用［M］．北京：国防工业出版社，1999．

［10］OSHIMA H．Automatic train operation system by predictive fuzzy control［C］∥Artificial Intelligence for Industrial Applications，1988．IEEE AI’88，Proceedings of the International Workshop，1988：485－489．

［11］YASUNOBU S．Application of predictive fuzzy control to automatic train operation controller［C］．Proc．of IECON’84，1984：657－662．

［12］刘 翔．城市轨道交通列车自动运行（ATO）最优控制策略的研究［D］．北京：北京交通大学，2011．

［13］周 明，孙树栋．遗传算法原理及应用［M］．北京：国防工业出版社，1999．