基于经济诱发效应的物流网络综合优化研究＊

（河海大学港口海岸与近海工程学院水运规划与物流工程研究所 南京 210098）

0 引 言

随着全球经济一体化和我国对外贸易的发展，作为区域经济发展的源动力，物流系统的作用日益增大．系统科学地规划区域物流网络不仅事关物流业的发展，也关系到区域经济整体实力的提升．

国际上对于区域物流网络优化的已有一些深入的研究［1］，包括经典选址问题及其与车辆路径［2］、库存管理结合［3］．相关学者运用运筹学原理进行物流网络布局，提出了：布局模型、布局－分配组合模型、布局－路径联合模型等模型．Georgako Poulos［4］研究了企业运作效率和市场营销的物流配送网络的优化问题．Jang［5］研究了企业的生产和配送的组合网络设计模型．相对而言，国内对区域物流网络布局优化方面的系统理论研究较少，如王伟等基于引力模型和加权Voronoi图提出区域物流节点协调布局优化模型及其高效求解算法［6］．张得志［7］从静态和动态不同角度入手，构建了4个区域物流节点布局优化模型．

综合国内外研究现状，现有物流网络布局模型，大都是研究标准的3层或多层结构，但随着经济的发展，日趋复杂的区域物流网络结构，必须考虑多级共存的混合物流网络设计问题；现有优化模型的目标函数，只考虑了运输费用和设施建设费用，而忽略了库存费用、订货费用等，关于物流网络格局变化对于区域物流生成量、区域经济发展以及区域间联系与合作的贡献等方面的考虑较少；此外，以往的研究将区域物流节点与区域物流通道的优化割裂开来，缺少对区域物流网络的综合研究，因此，对能够提供多产品、多功能服务，适应多货种多成本运作的混合区域物流网络综合优化的研究非常必要．

区域物流网络优化实际上是一个博弈问题，本文综合考虑区域物流网络运输、仓储、作业成本以及区域物流网络格局变化对区域物流生成量的影响和区域经济的拉动效应，构建区域物流网络综合优化的双层规划模型．将贪心法和遗传算法相结合对区域物流网络双层规划模型进行求解，实现区域物流网络的整体、动态、多层次性优化．

1 基于经济诱发效应的区域物流网络优化模型的构建

1.1 模型假设

1）网络中货源发生点和吸引点的位置、原始发生量和原始吸引量以及各点间的原始物流量均已知．

2）备选节点的位置、最大容量已知，原始交通网络预先确定，预选通道的起始点、最大容量已知．

3）物流费率已知，不受市场波动影响，且运输费用为线性函数，仓储费用受到物流节点规模影响．

4）各备选节点、备选通道的基建费用由固定费用和变动费用构成，费率已知．

5）区域物流需求量全部由物流节点中转，即源点与需求点间不存在直供量，但是源点层与物流节点层之间，物流节点层与需求点层之间存在直接运输量，将直供量作为对于通道的外部生成量来考虑．

6）假设货物或者物流服务是同质的，具有相同的价值和装运条件，对物流链具有同样的选择行为，物流链的选择遵循效用最大原则．

1.2 模型变量与参数

根据区域物流网络的特点，对一般的区域物流网络进行符号定义．

W为全部物流路径起讫点对，用有向弧表示的集合，对于 ∀w＝ （i，j）∈W，i为w 的发送地点，j为w的到达地点；

p为集合W 的子集，可表示为p＝ （w1，w2，…，wk），可表示区域物流通道方案，包括已有通道和规划通道；相应的u是集合U的子集，表示区域物流规划通道方案；

U为备选物流路径，用无向弧（或者回路）表示的集合，对于 ∀u＝ （r，s）∈U，r和s表示u的2个端点，u为由（rs）与（sr）组成的一个回路；

B＝［bi］K．其中：bi为物流节点布置在备选位置i的变动成本（包括用地和建设成本）；

wi为物流节点i的仓储规模；

ui为物流节点i的仓储费率；

vi为物流节点i的中转费率；

Tr为物流需求点r的平均库存周期；

A为物流网络中路段的集合，包括已有的路段和新增的备选路段；

xa为路段a上的物流量，它们组成的向量为x＝（x1，x2，…，xn），n是路段总数；

ta为路段a上的成本函数，它是路段物流量的函数ta＝ta（xa，ya）；

ya为路段a的通行能力增加值，共m个，它们组成的向量为y＝（ya1，ya2，…，yam）；

ga为路段a上通行能力增加ya所需的投资；

S为区域物流网络（包括通道或者节点）总投资上限；

a，k，r，s依次分别为路段下标，路径上标，发送源下标，吸引源下标．

1.3 优化模型

1．3．1 诱发物流量的预测

借鉴交通预测中的诱发交通量提出诱发物流量的概念，通过有无项目的比较［8］，提出如下诱发物流量模型．

式中：Drs，D′rs为网络优化前后需求点对r和s之间的总成本；qrs为网络优化前需求点对r和s之间的物流量；Δq′rs为网络优化后需求点对r和s之间的诱增物流量；Sr，Ts为网络优化前需求点对r和s的物流产生量和吸引量；α，β，γ，K 为模型参数，由现状OD及现状网络利用最小二乘法进行标定．

1．3．2 诱发物流量与诱发经济增长的关系

假设诱发物流量与诱发经济量呈正比关系，则：

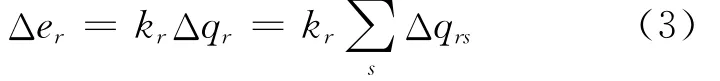
式中：Δer为小区r的诱发经济增长量；Δqr为小区r的诱发物流量；kr为小区r的诱发经济增长系数．

1．3．3 基于经济诱发效应的区域物流网络综合配置优化模型的构建

物流节点和物流通道是相互关联的．因此，研究物流节点和物流通道的协同优化问题非常必要．

根据物流网络网络总投资限制，有

式中：T1，T2分别为物流节点和通道的运营期，这里假定物流节点、通道运营周期一致；r为折现率．

区域物流网络的总运营成本包括运输、中转与仓储成本，可表示为

式中：θ为仓储规模效应因子（0＜θ＜1），wi＝

本文构建双层规划模型来表达物流网络布局问题：上层以区域物流网络单位效益－成本的最小化为目标．下层优化问题可视为物流链分配问题，下层决策者是用户，其不能改变方案，但能根据自身的需要选择物流服务链．建立基于经济诱发效应的区域物流网络优化的双层规划模型如下．

式（7）～（8）是以规划者为领导者、用户为跟随者的双层决策模型．式（7）是规划者的愿望；式（8）是用户均衡模型，其解是在均衡状态下各路段上的流量．

2 算法设计

考虑区域物流网络的复杂性和双层规划模型作为NP问题的特点，本文选择GA算法与贪心法相结合对网络优化问题进行求解．

2.1 初始解的确定

本文采用贪心法获得模型的初始解，假设初始解的优化目标为M0个物流节点和N0个通道．步骤为：

步骤1 令当前选中设施点数p1＝M，线路条数p2＝N，即将所有M个候选点和N 条候选通道都选中．

步骤2 将物流需求在物流网络中按照最小费用路径进行分配，求出网络费用F．

步骤3 若p1＝M0，p2＝N0，求出网络费用F后比较每一步的最小方案，其中的最小方案为优化方案，停止；否则，转步骤4．

步骤4 从p个设施候选点和线路中确定取走点或线路取走点本身代表了费用最高的点或线路．

步骤5 从候选点集合中删去取走点，令p＝p－1，转步骤2．

2.2 方案优化

采用遗传算法对区域物流网络布局方案进行优化，基本思路为：确定上层决策变量即物流网络规划方案的编码方案，随即产生初始群体；分析区域物流网络变迁对区域物流需求及其分布的影响，进而产生新的区域物流OD；通过求解下层模型得到每一个布局方案下物流需求对物流链的选择方案及其对应的区域物流分配结果，进而可以计算上层目标函数值从而得到不同个体的适应度．对这一群体进行选择、交叉、变异遗传运算，若干代后，算法收敛于最优物流节点规划方案．在区域物流网络优化中，编码采用实数编码，适应度函数采用上层问题的目标函数，针对约束条件在适应度函数中加入惩罚因子进行处理，选择操作采用基于“排名”的轮盘式选择算子，交叉操作采用单点算术交叉．

3 实例分析

本案例旨在对苏南高速公路物流服务网络进行优化，由于数据资料欠缺且难于收集，本案例中的部分数据为虚拟或由计算机生成．实例的道路交通网取自苏南高速公路路网（2006年），见图1．现状交通量和物流量取自2006年3月15～17日的苏南高速公路网多路径交通调查数据，物流车辆的出行选择特性根据Logit模型拟合得到，现状物流节点为0个，预选物流节点为15个，其规模限制为20 000；现状通道采用2006年的高速公路网方案，生成7个预选通道方案；有110个物流OD点，案例其他数据由计算机随机生成．

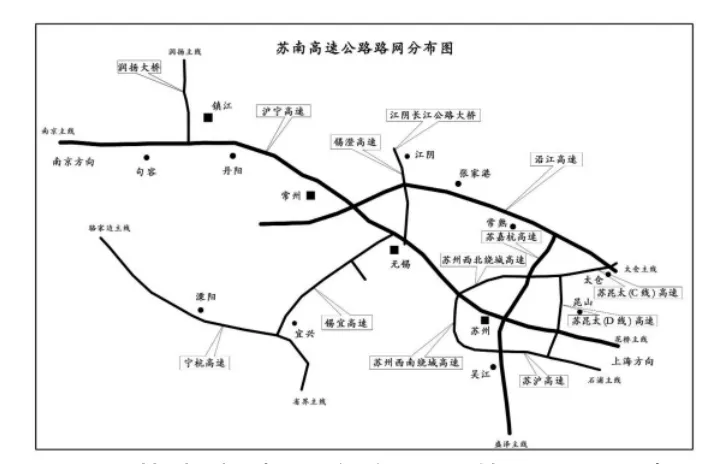
图1 苏南高速公路路网现状图（2006年）

假设物流节点间的单位运输费用为10，节点到非节点的单位运输费用为12，非节点到节点的单位运输费用为15，非节点间的单位运输费用为18，中转费率为1；物流节点单位固定投资费用为1 000，变动投资为1；物流通道固定投资费用为5 000，变动投资为5；通道的建设按照车道数量来设计规模；设区域的单位库存周期为30d，库存费率取0．1／（单位·d），仓储规模效应因子取0．5，总建设资金取275 000，优化前区域总经济效益取1．考虑物流量OD在物流链中的运输、仓储以及装卸作业等环节中的广义消耗．

在Delphi和SQL Server2000平台下编写程序，在实验过程中，通过调整参数实现区域物流网络优化．以现状方案为初始解，其目标函数值为2．820×109；遗传算法种群规模取50，最大仿真代数取100，变异概率取0．02，交叉概率取0．6．优化运行过程见图2．200次后的结果趋于最优解，其目标函数值为2．431×109，与现状方案相比，优化方案单位效益－成本下降了13．88%，表明优化后的物流网络成本显著下降，推动了区域经济发展，优化方案见表1．

图2 遗传算法优化过程图

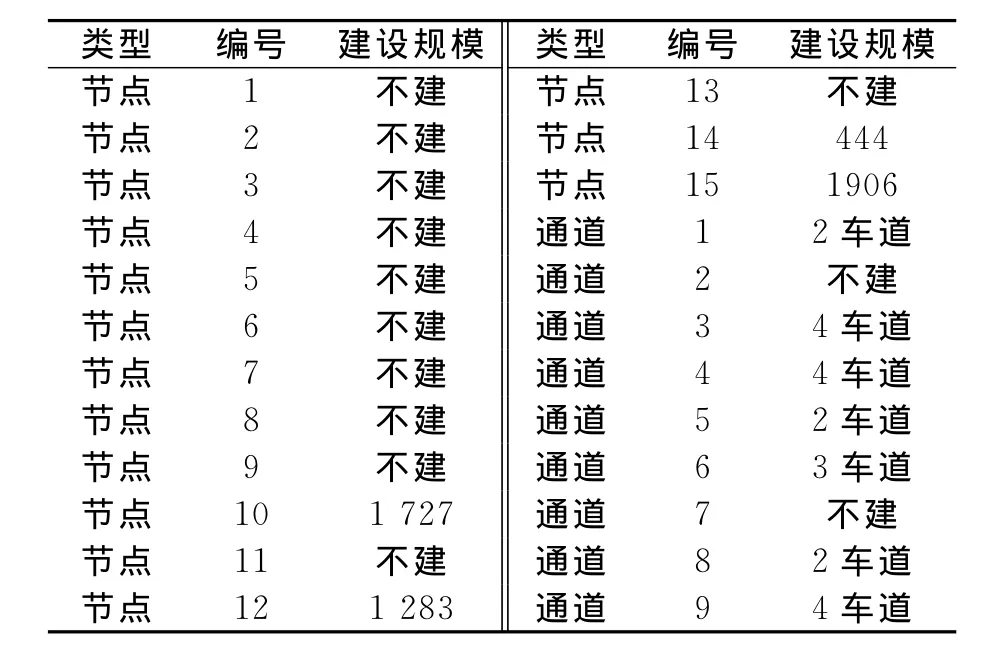
表1 遗传算法迭代200次以后的解

4 结束语

本文综合考虑众多因素与成本，构建基于经济诱发效应的多成本混合结构物流网络优化的双层规划模型，将贪心法和遗传算法相结合对模型进行求解，为区域物流网络优化提供了方法借鉴．但由于研究能力和时间的限制，成果尚有许多不足之处：（1）区域物流优化中不确定因素较多，对不确定条件条件下区域物流网络可靠性诊断与优化的研究有待于进一步深入；（2）由于数据量大且难以收集，案例采用了一些虚拟数据，且模型中的部分控制参量取经验值，对于这些不足，力求在以后的工作中通过实际调查来弥补．同时，未来将进一步改进优化模型和算法，力争研发一个集成各种优化策略方法的区域物流网络优化的辅助软件．

［1］LIA Feiyue．Very large－scale vehicle routing：new test problems，algorithrns，and results［J］．Computers ＆ Operations Research，2005，32：1165－1179．

2REVENE C SEISELT H A．Location analysisA synthesis and survey［J］．European Journal of Operational Research，2005，165：1－19．

［3］ MARIANOV V，SERRA D．Location－alloeation of multiple－server service centers with constrained queues or waiting times［J］．Annals of Operations Research，2002，111：35－50．

［4］GEORGAKOPOULOS A，MIHIOTIS A．Distribution network design：an integer programming approach［J］．Journal of Retailing and Consumer Services，2004（11）：41－49．

［5］JANG Yangja．A aombined model of network design and production／distribution planning for a supply network［J］．Computers ＆Industrial Engineering，2003，43：263－281．

［6］王 伟，封学军．基于加权Voronoi图的连续型物流节点布局优化［J］．武汉理工大学学报：交通科学与工程版，2011，35（6）：1103－1107．

［7］张得志，谢如鹤，李双艳．物流园区布局优化模型及其求解算法研究［J］．武汉理工大学学报：交通科学与工程版，2008，32（6）：1048－1051．

［8］章锡俏，王守恒，孟祥海．基于经济增长的高速公路诱增交通量预测［J］．哈尔滨工业大学学报，2007，39（10）：1618－1620．