基于双层规划模型的公交枢纽内部流线优化＊

（北京建筑大学土木与交通工程学院 北京 100044）

0 引 言

公交枢纽内部流线设计的水平直接影响到枢纽内部的换乘效率．枢纽内部流线组织的好坏通常是评价枢纽设计水平的重要重要指标．对于枢纽内部流线的研究已有一些成果，分别是从公交枢纽设施布局、公交枢纽内部流线组织设计等方面展开的．

综合国内外的已有研究成果可以发现，有关枢纽设施布局的研究可以分为2个方面：（1）从设施的角度出发，通过相关的研究达到优化的目的；（2）从旅客的角度出发，以对旅客的服务水平为依据进行优化设计．概括来讲，对枢纽设施布局的研究集中在机场、城市轨道交通为主要交通方式的枢纽上，研究范围广，对于设施优化布局、依据建设成本的设施布局、不同服务水平下的设施布局等方面都有成果．

对于枢纽内部流线组织、设计、优化而言，研究成果较为丰富．综合国内外的研究成果，相关研究可以分为以下几个方面：首先，通过流程图等手段使得流线形象化，使得后续研究得以简单开展；其次，通过仿真建立旅客行走模型等技术手段寻找流线中的“瓶颈”区域，可以有针对性的进行枢纽内流线的优化研究；最后，通过分析客流的行走特征、客流流线的特性，依据参与者的自身特点，设计、优化枢纽设施等影响因素最终达到优化内部流线的目的．

对于枢纽内部流线的布置方法为设施平面布置方法（system layout planning，SLP），其原理是通过各作业单位之间的紧密关系对各设施进行平面布局以及优化．这种方法主要用于工厂流水线的平面布局，其使用效果较为突出．

综合上述对于枢纽内部流线的研究可以发现，现存的所有研究成果对于枢纽在设计阶段的流线优化涉及内容较少．SLP法虽然可以起到一定的作用，但是由于其对设施前后顺序有严格要求且流线相对固定，所以不能完全适用于枢纽内部的流线设计．

1 公交枢纽内部流线优化的问题描述

通过分析旅客在枢纽内部换乘的特性，可以发现其与道路交通流有以下类似特征：（1）公交枢纽内的流线类似于城市道路的路网．在公交枢纽内各条流线上的流量要受到流线上设施的限制，正如同道路路网上各条道路的通行量要受到道路通行能力的限制；（2）枢纽内各种交通方式类似于城市间各个小区，而各种方式间的换乘量相当于各个小区间的 OD量［1］；（3）旅客与驾驶员的行为类似，即都希望找到时间、距离或费用最短的路径．

基于以上3点原因，本文将利用城市交通规划中交通分配的思想，建立公交枢纽内部流线的优化模型．通过对枢纽内相关设施以及流线的调整，优化旅客流量在流线上的分配，最终达到优化枢纽内部流线组织、提高枢纽换乘效率的目的．

2 公交枢纽内部流线优化的关键问题

2.1 双层规划模型的选定

在城市交通规划中，用户平衡（user equilibrium，UE）和系统最优（system optimization，SO）是2种最常用的交通分配方法．在枢纽内部流线设计中若采用类似的分配方法就涉及到采用哪个原则合适的问题，即枢纽的使用者与枢纽的管理者之间的关系．若按照UE模型对流线进行优化设计，那么调整后的流线对其使用者即旅客是最优的，可以满足旅客的期望，但是对于枢纽的管理者不一定是最优的，这是枢纽的管理者不希望看到的；同样，如果按照SO模型进行流线的优化设计，那么调整后的流线是对枢纽内整个换乘系统最优的，可以满足管理者的期望，但是就个别旅客而言可能需要绕行，使其换乘成本增加，这也是不现实的．

为了满足双方的需求，采用双层规划的方法可以有效地解决使用者与管理者之间的关系，即UE与SO的协调统一．

2.2 时间函数的确定

公交枢纽内部乘客的行走特征可以用特定的乘客步行时间和相应的流量来表达［2］．BPR（路阻函数）模型是美国公路局通过对路段交通量进行大量分析后，由回归分析得到的，具有函数形式简单、分配模型求解速度快的特点［3］．本文拟采用BPR（路阻函数）模型进行公交枢纽内部客流行走时间与客流量的分析研究．BPR函数的模型如下．

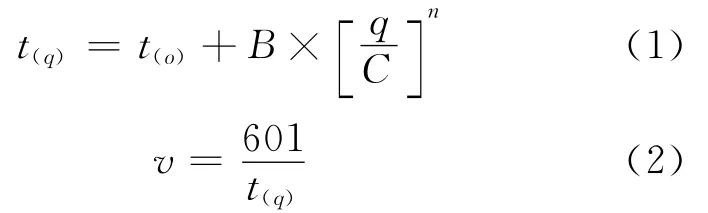
式中：t（q）为流量为q时通过相关设施的行走时间，s；t（0）为自由流时，相关设施的行走时间，s；q为对应相关设施的行人流量，人／（min·m）；B，n为待定参数；C为相关设施的行人通行能力，人／（min·m）；v为相关设施上旅客的步行速度，m／min；l为相关设施的长度，m．

由各设施的交通特性分析可以得到所要研究的设施上旅客步行速度与流量的关系，通过上述两公式可以将其转化为耗时与流量的关系，进而得到不同设施时间函数的模型．

基于调查数据，对于公交枢纽内各设施的时间函数汇总，见表1．

表1 设施时间函数汇总表

3 公交枢纽内部流线优化设计模型

3.1 模型建立

对于公交枢纽内部流线的优化是以流线系统的效率最高为目标的，但是对于流线上的旅客个体来说，他们在选择线路时显然不会关心个人出行对换乘流线系统的影响．因此，本模型将以流线系统优化模型作为上层模型，以旅客个人出行的用户最优模型作为下层模型．上层模型的换乘量和行走时间由下层模型提供，按照上述思路建立公交枢纽流线优化的双层规划模型．

3．1．1 上层模型

通过以下2方面考虑系统最优．

式中：fa为设 施a 的 流 量；ta，q（f）为 设 施a 在 流量为f时的通行时间．

3）构建上层模型

式中：Ea为设施a的广义费用；δ为旅客的时间价值．

在上层模型中，模型的目标函数是minEtot，实际上是建立了一个在建设费用较小的情况下优化枢纽内的流线，使得旅客的出行时间最小．约束条件式（6）为建设成本的限值．

模型中加入了旅客的时间价值δ，其主要目的是为了将换乘时间转化为广义的费用．时间价值可以分为资源价值以及行为价值，其中资源价值主要用于交通运输项目的评价等方面，而行为价值则是用于交通方式的分担、预测．在本模型中，取其第二种意义．对于其行为价值的计算方法如下［4］：

式中：Y为人均年平均工资，元／a；n为每年工作的周数，周／a；tw为每周工作小时数，h／周．

在本文中取n＝50周／a，tw＝40h／周，则式（8）为在时间利用系数为0．5的情况下，社会劳动者的单位时间价值．

3．1．2 下层模型

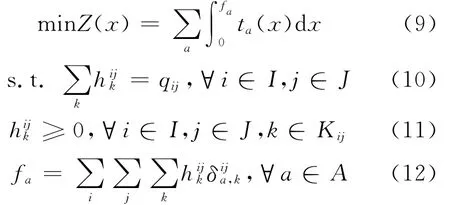
式中：I为换乘出发地集合；J为换乘目的地集合；qij为OD对i和j之间的换乘量为OD对i和j之间的第k条路径上的流量；为0－1变量，表示如果路段a在连接OD对i和j的第k条路径上，其值为1否则为0．

下层模型是对某些实际流线上的设施进行调整后，使其通行能力得到改变．

3.2 模型算法

有关双层规划问题的解法，到目前为止可以分为四类，大概有十几种．主要有：极点搜索法（extreme point search method）、库恩－塔克法（KT法）、下降法（descent method）、直接搜索法（direct search method）［5］．考虑到模型求解的效率和准确性，本文采用遗传算法（GA）与模拟退火法（SA）的混合算法［6－7］求解公交枢纽内部流线优化的双层模型．算法流程见图1．

图1 GASA算法流程图

4 案例研究

4.1 背景概述

本文选取北京某公交枢纽作为实例研究的对象．此公交枢纽作为集地铁、地面公交、出租车等多种方式与一体的公交枢纽之一，承担这地区与中心城以及与外围新城之间的联系．为了进一步方便此地区居民的出行以及加强和改善中心城与新城的联系，需要对此公交枢纽站进行规划设计．

4.2 换乘量预测

4．2．1 换乘类型分析

根据枢纽站的主要功能以及枢纽站功能定位分析，此枢纽站是一个以轨道交通和公交换乘为主，辅以自行车、出租车等交通方式的换乘枢纽．根据该地区控规，枢纽站周边以住宅为主，以500 m服务半径作为直接吸引范围进行估算，在此范围内大约有1．8万居民，在此服务范围内的居民将以步行至枢纽站为主，换乘地铁、公交等交通方式．

4．2．2 换乘量预测分析

预计2020年枢纽站全日客运量将达到21万人次，高峰小时客运量将达到3．6万人次，其中2条地铁线路之间的换乘量在全日及高峰小时将达到3．5万人次和0．6万人次．见表2．

表2 2020年枢纽各种交通方式高峰小时换乘集散量预测［8］ 万人次／h

4.3 枢纽内流线优化设计

本枢纽最大的换乘量出现在2条地铁线路之间，显然这2条地铁线路之间的设施设计的优劣会对枢纽整体换乘效率有明显的影响．在最后的建筑方案中，采用的是通过地下2层到地上2层的电梯直接连接两种交通方式的方法，在设计过程中对这2种交通方式间的换乘要有其他的方案．在这里主要讨论2种设置方式：（1）通过地下通道将地铁与地铁之间的换乘旅客与其他换乘旅客彻底分离，通过通道将地铁与地铁之间的换乘旅客引到另一侧，通过电梯将旅客送到另一种换乘方式；（2）将所有的客流引到地面层，采用换乘大厅的方式，分别通过2组电梯达到地铁与地铁2种交通方式之间的换乘．

4.4 枢纽内部流线优化设计模型

基于上述3种换乘方式，本节将采用本文第3节所建立的双层规划模型建立枢纽内部流线优化模型，此模型采用GASA方法求解．

4．4．1 参数的确定

1）在GASA算法中，首先需要确定的是在遗传算法中的编码，由于建立的模型有3种换乘方式（见图2～图4），本次的模型编码采用二进制的6位编码，具体编码意义见表3．

2）在上层模型中所涉及到的时间价值可以由式（8）计算得到，其中2010年北京市人均可支配收入由《2010年北京统计年鉴》可以得到，为29 072元．

表3 编码意义说明

图2 方式一

图3 方式二

图4 方式三

3）退火遗传算法中的基本参数为：初温为100冷却系数为0．9终止温度为1变异系数为0．9，变异概率为0．02，初始种群为10．

4．4．2 计算结果分析

采用MATLAB编程，通过遗传算法工具箱经过迭代计算得到最后的计算结果见表4．

表4 计算结果对比分析

通过计算结果对比分析表可以看出，当方案是“0 1 0 0 0 1”时，建设成本为84万元，为所有迭代中最小，其所对应的时间价值成本为113．1；方案“1 1 0 1 0 0”的时间价值为112．4，是所有方案中最小，但其建设成本高达144万元．综合考虑后方案“0 1 0 0 0 1”为最优方案，即采用换乘大厅的方式，分别通过两组电梯达到地下2层与地上2层旅客之间的换乘．

5 结束语

本文针对交通枢纽建设的热点问题，以城市公共交通枢纽的根本功能“换乘”为出发点，采用双层规划的方法建立了公交枢纽内部换乘流线优化模型，并设计GASA算法进行求解．采用本方法不仅可以更容易的发现换乘设施之间的连接是否存在问题，而且可以为关键流线的方案设计提供比选依据，使枢纽内部流线的设计更加合理．针对北京某枢纽的案例研究表明，模型对于公交枢纽内部流线优化设计是非常有效的．

［1］王英男．大型综合交通枢纽站客流预测及组织优化方法研究［D］．北京：北京交通大学，2008．

［2］王志刚．上海轨道交通车站乘客走行时间函数的分析［J］．城市轨道交通研究，2010（12）：57－60．

［3］WILLIAM H K，CHEUNG C Y．Pedestrian speed／flow relationships for walking facilities in Hong Kong［J］．Journal of Transportation Engineering，ASCE 2000，126（4）：343－349．

［4］王金南．论环境成本内部化及政策选择［J］．中国人口、资源与环境，1997，17（1）：63－68．

［5］陆化普．交通规划理论与方法［M］．北京：清华大学出版社，2007．

［6］焦朋朋．基于交通效率的城市道路网络优化［J］．清华大学学报：自然科学版，2005，45（3）：297－300．

［7］王 凌，郑大钟．一种GASA混合优化策略［J］．控制理论与应用，2001，18（4）：662－664．