WN齿轮副耦合振动及动态应力仿真的研究

张国庆，李玉光*，陈殿华

（大连大学 机械工程学院，辽宁 大连 116622）

WN齿轮副耦合振动及动态应力仿真的研究

张国庆，李玉光*，陈殿华

（大连大学 机械工程学院，辽宁 大连 116622）

基于WN弧齿轮传动特征建立了多自由度切-径-轴及系统误差耦合振动动力学模分析型。利用PROE建立齿轮三维实体模型，通过PROE软件和Ansys软件数据接口将WN弧齿轮三维模型导入Ansys软件中进行了3维冲击动力接触模拟分析，利用施加载荷进行了WN弧齿轮的应力分析，仿真出WN齿轮齿面接触的等效应力云图。在ANSYS/LS-DYNA中构建了齿轮钢柔性体动态接触模型，以用于齿轮转动的动态分析，结果表明WN弧齿轮的切向与轴向方向的振动明显大于径向的振动。

WN齿轮；动态接触；应力仿真；耦合振动

0 引言

WN齿轮也名为双圆弧齿轮，以其良好的跑合性能、高承载能力、有效寿命长等优点和独特的多点啮合方式和凸、凹齿接触，其接触强度比渐开线齿轮在相同情况下更大。因此在石油化工、汽轮机、航空直升机等领域得到广泛应用。然而 WN齿轮也具有啮合状态复杂、载荷反复交变等特点[1]。为了改善齿轮传动的静动态特性和运转性能，对 WN齿轮的啮合性能、接触状态进行仿真分析是迫切需要的，这样也能更好确定齿面压力分布、综合啮合刚度、齿间载荷分配等。

1 WN弧齿轮传动系统的动力学模型

1.1 WN弧齿轮齿面的基本方程

用GB/12759－1991型号的WN齿轮作为研究对象，WN齿轮的齿廓是由凸弧、凹弧、凸凹弧的过渡圆弧、齿根圆4段圆弧构成。每个圆弧都由各自的半径、圆心位置确定。WN齿轮齿廓的公式方程为：

式(1)中：r为齿轮节圆半径，ρ为相对曲率半径，β为螺旋角，e为凹齿接触点处槽宽，N为齿廓圆心相对所选坐标轴的偏移量，φ为齿轮转角。

1.2 传动系统动力学方程

[2、3]，考虑切-径-轴方向及系统误差的耦合作用，利用PROE建立齿轮三维实体模型建立动力学模型。如图1所示，为x轴、y轴、z轴方向的平移振动位移；为主从动齿轮绕 z轴方向的扭转振动位移；为主从动齿轮沿y轴、x轴方向的摆动振动位移。WN齿轮传动系统的广义位移列阵可表示为列向量：

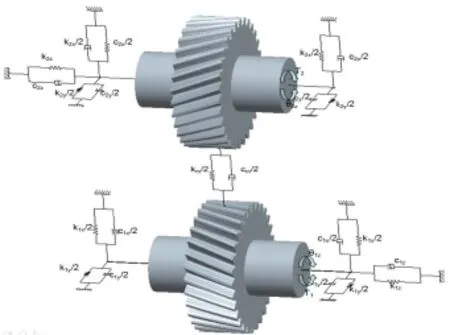
图1 WN齿轮副啮合的动力学模型

由此列出 WN齿轮传动系统各振动方向的运动微分方程，得到该传动系统的振动方程为：

以上齿轮传动系统中的阻尼系数和刚度均由试验方法获得。用矩阵表示上述运动方程为：

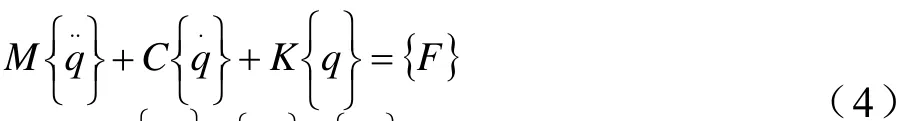
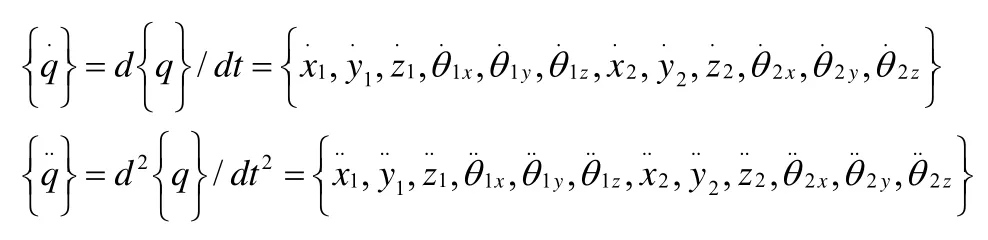
2 模型求解方法及数值求解

2.1 模型求解方法

用直接积分法（也称时间变量离散法）求解（4）中的动力学方程。即把时间区间划分成n个时间均匀步长 tΔ。首先用t0时刻的推算出时刻的位移值、速度值和加速度值，然后再逐步积分求解出每个瞬时时间的，本文采用Newmark-β法，它是线加速度作为整个区间的实际加速度，即

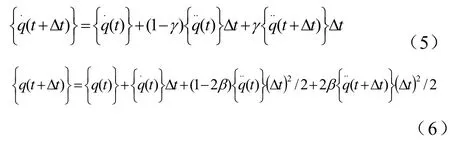
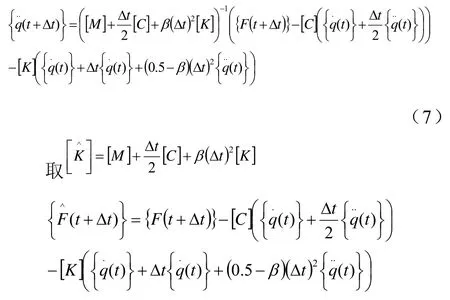
则（7）变为

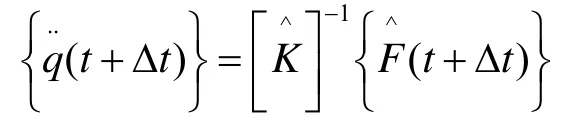
(8)

2.2 模型数值求解

由2.1的解析可知，齿轮耦合振动系统的动态响应求解的程序用Newmark-β法和数值方法进行编写[4]，利用这个程序，对齿轮接触的动力学运动微分方程的进行计算，得到 WN齿轮耦合振动系统中各自由度的时间响应历程，并且计算出其振动加速度、速度和各坐标轴方向的动态力的相应值。如图2所示，其计算程序框图为。

图2 齿轮动态响应的计算程序框图

3 WN齿轮传动系统的动态仿真

3.1 WN齿轮建模

由于 WN齿轮齿面复杂，使用齿面齿廓方程式构建完整的齿轮齿面较麻烦。故通过PROE软件 和Ansys数据接口将WN弧齿轮三维模型导入Ansys软件中，并对模型划分网格，施加载荷，在Ansys软件中进行WN弧齿轮的应力分析[5]。分析模型如图3：

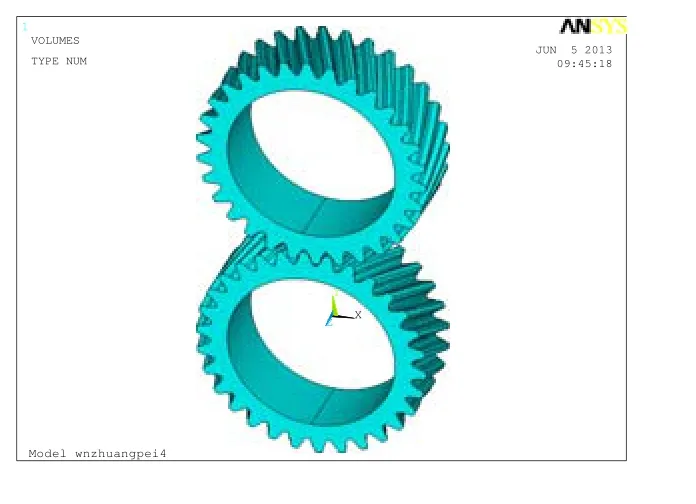
图3 WN弧齿轮导入的分析模型

3.2 齿对动态接触模型

单元选择：针对刚柔体模型，选用SOLD164单元和SHELL163单元。SOLD164单元是三维实体单元，为8节点六面体单元，各节点拥有9个自由度，将用于齿轮轮体。而此单元没有旋转自由度，不能施加转速和转矩。SHELL163单元为二维实体单元，弥补了这一缺陷，用于齿轮内圈表面的单元划分。将SHELL163定义为刚形体约束其旋转自由度，这样有利于齿轮扭矩和转速的施加。

材料属性和实常数的设置：对于 SHELL163单元，设置为S/R Co-rotional Hughes-liu，即所谓的面内多积分改进型，以避免沙漏变形在分析工程中出现。而对于SHELL163单元，其均匀厚度设置为0.1。对于齿轮材料属性，其密度设置为7.81-6 kg/mm3，弹性模量设为2.05e8Mpa，泊松比为0.25。在材料的设置中还有必要对旋转和平移设置约束。两齿轮的参数均设置为：translational constraint parameter-7(设置x,y，z方向的位移约束)，rotational constraint parameter-4 (设置x和y方向的旋转约束)。

划分网格和创建PART：分别对大小轮体采用弹性材料1、3，而其内圈内圈则采用刚性材料2、4，分别进行网格划分(如图4)，然后创建PART 1、2、3、4；其中2、4是刚体。在前面定义材料是已经将刚体定义为除了绕 Z轴方向旋转，其他所有约束进行了约束。

定义接触类型：定义柔体PART1和PART3为接触对，选择自动单面接触，即物体自身或者物体之间在任意时间内的接触情况将由程序自动判断。

加载：给刚体PART2加载恒定的刚体角速度，刚体 PART4加载恒定的刚体转矩[6]，这里假设输入轴的转速和输出轴的转矩都是恒定不变。

图4 WN弧齿轮的网格划分模型

3.3 多齿对齿轮的动态仿真

利用ANSYS的非线性动力分析模块进行WN齿轮的动力学接触仿真分析[5.6]，得到了齿轮轮齿在一个啮合过程中等效等值应力的变化情况，仿真的动画在0.001 s内共有22帧，这里仅列出4幅连续的应力应变云图（如图5所示)。同时利用Hertz应力公式计算的相应理论值，将ANSYS仿真出的轮齿等效等值应力与相应的理论值相比较，发现其偏差不大，而且趋势相同。

在LS-POST中选取齿根单元4101和单元70397，一个节点11364（如图6），分别仿真单元的等效应力随时间的变化曲线，齿根等效应力随啮合时间的增加，先是增加然后又减小，与事实啮合情况相符。

图5 啮合齿轮的动态等效等值应力图

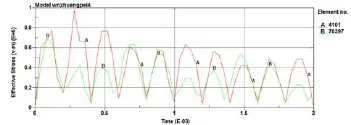
图6 啮合中节点4101和70397的应力变化

图7所示，在主动齿轮加入转速和转矩，被动齿轮则加入相应的转速和转矩，得到的等值应力分布图，如图我们可以看出，在齿根凹弧处，其齿根应力最大，故而会产生断齿等齿轮失效情况，这与实际情况相符。

如图8所示，节点11364在X、Y、Z（X为齿轮切向方向，Y为齿轮径向方向，Z为齿轮轴向方向）方向的加速度随时间的变化曲线，再看节点11364分别在切向、径向、轴向方向的加速度随时间增加的变化情况，其中切向与轴向方向的加速度明显大于径向方向的加速；从加速度的情况我们可以得出在切向与轴向方向的振动明显大于径向的振动。

图7 啮合中耦合动载瞬时作用的应力分布

图8 啮合周期内各方向的加速度变化

4 结论

(1) 采用切-径-轴 3方向及系统误差耦合建立WN弧齿轮动力学模分析型。与工程实际更加接近。通过PROE软件和Ansys软件数据接口将WN弧齿轮三维模型导入Ansys软件中, 建模方便。

(2) 基于ANSYS/LS-DYNA显式动力程序，建立了齿轮动态刚柔性体计算模型，真实地模拟齿轮啮合情况，得到了直观清楚的仿真结果。

利用 history模块，成功的仿真出单元等效应力曲线与节点的加速度情况。得到了圆弧齿轮啮合过程中的切向、轴向、径向方向振动情况，为齿轮参数设计和减少齿轮传动的噪声提供了理论依据。

参考文献：

[1] 陈殿华, 李成超. 基于负载与啮合特征的WN齿轮传动接触强度分析[J]. 工程设计学报, 2012, 19(4): 294-297.

[2] 王立华. 汽车螺旋锥齿轮传动耦合非线性振动研究[D].重庆: 重庆大学, 2003.

[3] Dianhua Chen, Guoqing Zhang, Xi Chen. Research on nonlinear vibration and bend strength character of WN gears pairs in meshing [J]. Advanced Materials Research, 2013, 706-708: 1537-1540.

[4] 陈殿华, 李玉光. 基于弹流润滑与动力学耦合的WN齿轮传动的强度设计[J]. 工程设计学报, 2009, 16(5): 364-368.

[5] 屈文涛等. 双圆弧齿轮的有限元综合分析方法[J]. 机械强度, 2006, 28(3): 415-418.

[6] 李成超, 陈殿华, 李玉光, 等. WN齿轮传动的三维建模与啮合仿真析[J]. 大连大学学报, 2012, 33(6): 5-8.

The Study of Coupling Vibration and Dynamic Stress Simulation for WN Gear Pair

ZHANG Guo-qing, LI Yu-guang*, CHEN Dian-hua
（College of Mechanical Engineering, Dalian University, Dalian 16622, China）

Based on double arc gear characteristics and considering system error, a multi-degree-freedom (Tangential -Radial-Axial) coupled vibration dynamics analysis model was established. In this article, we established the three-dimensional solid model by using PROE, imported the arc gear three-dimensional model into Ansys software through the data interface of Ansys software and PROE software and conducted a three-dimensional simulation anasys of the impact of dynamic contact. By applying load, it conducted a stress analysis for double arc gear and gain the double arc gear's the effective stress clouds. Meanwhile, the rigid-flexible body of gear dynamic contact model based on ANSYS / LS-DYNA was established and the dynamic simulation anasys for WN gear was analyzed. The results demonstrated that the tangential and axial vibration of double arc gear is significantly greater than the radial vibration.

WN gear; dynamic contact; stress simulation; coupling vibration

TH132.41TP311.1

：A

：1008-2395(2013)06-0001-05

2013-08-30

国家自然科学基金项目（51075047）。

张国庆（1988-)，男，硕士研究生，研究方向：摩擦磨损及数值仿真技术；陈殿华（1953-），男，教授，研究方向：机械设计理论及CAD/CAE。

李玉光（1963-），男，教授，研究方向：机械设计。