舰艇沉没概率解析计算模型
2013-03-08浦金云陈晓洪
侯 岳,浦金云,陈晓洪
(海军工程大学动力工程学院舰艇安全技术系,湖北武汉 430033)
舰艇沉没概率解析计算模型
侯 岳,浦金云,陈晓洪
(海军工程大学动力工程学院舰艇安全技术系,湖北武汉 430033)
对影响沉没概率计算的要素进行分析,给出沉没概率的解析计算模型;然后,对解析计算模型的2个关键问题,即水密区破损概率计算模型和沉没判据模型进行了研究。考虑到武器炸点在三维方向上分布是独立的,建立了水密区破损概率计算的解析模型。分析舰艇沉没的判据指标,并建立基于支持向量数据描述的沉没判别算法。最后,使用此解析计算模型对某船模的沉没概率进行了计算,该算例说明了此解析模型的准确性。
沉没概率;破损概率;解析模型;支持向量数据描述;沉没判据
1 问题的提出
舰艇不沉性是舰艇生命力的主要构成要素之一,目前一般使用沉没概率对其进行定量地计算。通过计算典型威胁武器下的舰艇沉没概率,可以判断舰艇的设计方案能否满足预定的生命力设计要求,并可以对多种设计方案的优劣进行比较[1]。IMO海上安全委员会 (MSC)根据大量海损资料建立了基于概率计算方法的货船分舱和破损稳性规则,规则详细规定了沉没概率的计算方法[2]。然而,军船沉没概率的计算较民船更为复杂,需要考虑武器炸点和破损半径的随机性以及水密分区和工作环境的复杂性等[3]。
目前,国内在进行军船沉没概率计算时,使用的都是蒙特卡罗仿真计算模型。该模型需要对武器炸点进行上千次仿真计算,不仅计算量较大,而且其收敛问题一直没有得到很好的解决。为此,本文建立了沉没概率计算的解析模型,该模型不仅考虑了炸点分布的随机性,还考虑了武器破损半径大小的随机性,较好地解决了单发武器攻击下的舰艇沉没概率计算问题。不仅如此,目前国内在进行沉没判据的定义时,都是基于单指标是否超出阈值范围进行判别的,未对多指标综合评估下的沉没判据模型进行研究。因此,本文建立了基于多指标和样本学习的沉没判别模型。
2 影响沉没概率计算的要素
舰艇在受到武器攻击破损后,其沉没概率的大小主要与以下3个要素有关:
1)舰艇主水密区可能的破损模式。不同的破损模式,其破损后引起浮性和稳性指标减小的程度不同,因此,它直接影响着舰艇是否沉没的判别;
2)破损模式的发生概率。如果某个破损模式发生后,造成舰艇沉没的可能性较小,但该模式出现的概率较大,那么该模式对舰艇沉没概率的影响仍然可能较大;
3)舰艇沉没的判别逻辑。舰艇在战斗时的工作环境可能极为恶劣,因此,大风浪状态下的沉没判别逻辑设定也是影响舰艇沉没概率计算的关键要素之一。
假设舰艇主水密区可能的破损模式个数为N,破损模式i(i=1,2…N)的沉没逻辑变量取值为si,可能发生的概率为pi,则舰艇的沉没概率可用下式表示:
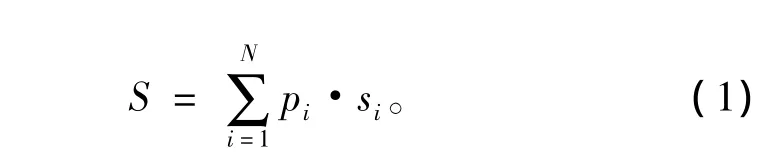
如果破损模式i会造成舰艇沉没,则si=1;否则si=0。在单发武器的攻击情况下,破损模式可以设置为相邻水密区的破损。因此要用式(1)进行计算,必须建立相邻水密区破损概率pi的计算模型和多个不沉性指标综合评估下的沉没判据逻辑。
3 水密区破损概率的解析计算模型
在以往的沉没概率计算研究中,一般是计算特定武器损伤范围下的沉没概率。然而,武器的损伤范围通常较难以确定,需要将其看作是一个在某均值附近服从某一分布的随机变量。本节将建立考虑破损半径大小随机性和炸点三维随机分布下的破损概率解析计算模型。
3.1 解析计算模型
假设武器的破损半径为r,r的概率密度分布函数为g(r),r出现的集合为R,武器炸点分布的概率密度函数为f(x,y,z)。在武器的破损半径r作用下,若特定破损模式对应的炸点分布区域为Ω(r),则特定破损模式的损伤概率可用下式表示:

在实际计算过程中,由于很难确定f(x,y,z)的具体解析函数,但是考虑到武器炸点在三维方向上的分布可以认为是独立的,则式(2)可表示为[4]

式中:f(x),f(y)和f(z)分别为武器炸点在X轴、Y轴和Z轴方向上的概率密度函数;X(r),Y(r)和Z(r)分别为在武器破损半径r下,特定破损模式对应的炸点在三维方向上对应的损伤区域。因此,只要确定f(x),f(y)和f(z)的解析模型,就可用式(2)对隔舱破损概率进行计算。
3.2 武器炸点沿单个坐标轴方向的分布规律
武器炸点在单个坐标轴方向分布的概率密度函数一般分为均匀分布、线形分布、三角形分布和正态分布4种。在X轴方向上,只有均匀分布、三角形分布和正态分布,没有线形分布;在Z轴方向上,主要考虑均匀分布和线形分布;在Y轴方向上,4种情况都有可能出现。
X轴方向上的均匀分布、正态分布和三角形分布的解析式,以及Z轴方向上线形分布的解析式如下:
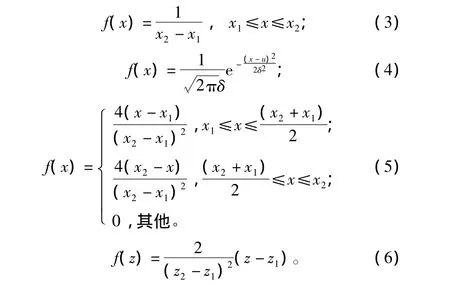
式中:x1和x2分别为武器炸点在X方向的极小和极大坐标;u为炸点的均值坐标;δ为炸点分布的方差;z1和z2分别为武器炸点在Z方向的极小和极大坐标。
在Y轴方向上解析形式与上述各式基本类似,本文不再做详细介绍。
3.3 模型应用举例
假设某水下武器破损半径大小服从正态分布,均值为ur,方差为δr;f(x)服从正态分布,均值为ux,方差为δx;f(z)服从线形分布,炸点在Z轴的极小和极大坐标分别为zd和zu。假设爆炸类型为接触爆炸,因此,不考虑炸点沿船宽方向的分布。以纵剖面为矩形的水密区的破损概率计算为例,如图1所示。
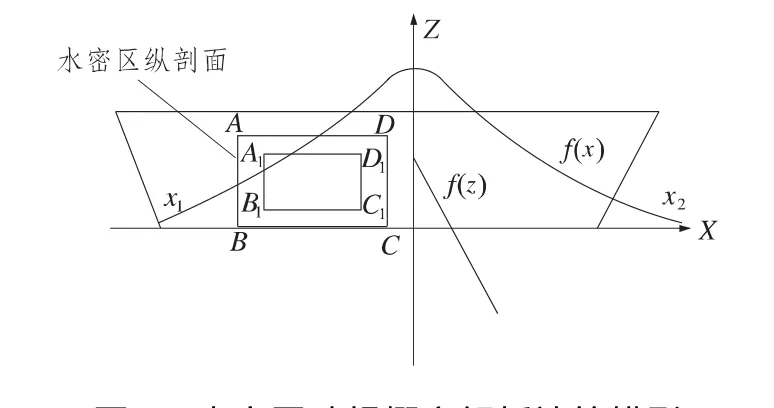
图1 水密区破损概率解析计算模型Fig.1 Damage probability analytic calculation model of watertight region
图1中,矩形ABCD和矩形A1B1C1D1边界间隔距离都是破损半径r。因此,对于水密区域ABCD,只有当炸点在区域A1B1C1D1范围内时,才会发生只有水密区ABCD破损的损伤模式。因此,根据式(2)破损概率计算建模的基本方法,可得:

对式(7)进行积分计算,即可求得水密区破损的概率值。如果对于某特定的损伤模式,积分公式较难求解,可采用牛顿-柯特斯公式法进行计算[5]。
4 基于SVDD的沉没判据模型
目前,国内外在对舰艇沉没判别逻辑定义时,基本上使用的都是单指标方法,即,只要存在某个指标超出阈值范围,就认为舰艇沉没。然而,舰艇沉没与否是多个指标综合作用的结果,因此需要建立其多指标的综合评判模型。
国外在进行判别指标阈值的设定时,一般是综合舰船的实际沉没案例以及船模典型模式下的破损案例进行的。也就是说,其一般是根据样本的沉没特征来设定指标阈值的。根据这一思路,可以使用样本学习的方法,建立舰艇沉没的判别模型。
由于在以往的不沉性评估分析中,一般得出的是舰艇处于安全状态下的样本,而舰艇沉没的样本获取的一般较少,也就是说只能得到两类模式中的一类样本。这种情况的模式识别,无法使用传统的人工神经网络及支持向量机进行解决。本节主要论述如何使用支持向量数据描述 (support vector data description,SVDD)进行沉没与否的模式识别。此方法主要用于处理单值分类问题,甚少用于异常样本的情况。
4.1 SVDD基本建模思想
SVDD的基本思想是把要描述的对象作为一个整体,建立一个封闭而紧凑的超球体,使得描述的对象全部或尽可能多地包含在这个球体内,而非该类对象没有或尽可能少地落入该球体内[6]。
它根据目标集的数据获得关于目标集的描述,主要用来检测新的样本是否与目标集的描述相似。如果相似则被目标集接受,否则该样本就是异常样本。
4.2 基于SVDD沉没判别模型
4.2.1 沉没判据单指标的设定
结合国内外沉没判据指标的设定现状,本文使用静平衡角θ、最小干舷fmin、最大扶正力臂lm、风浪下的稳度储备系数dyw、静风倾角θB及初稳度h作为沉没评估的单指标。因此,沉没判据的单指标向量x可以表示为
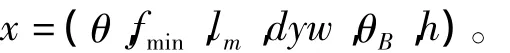
4.2.2 基于SVDD的沉没判别模型
假设目前共有某舰艇的N个不沉没状态下的样本集为
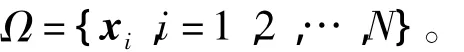
其中xi为沉没判据的单指标向量集。
舰艇不沉没状态时,可以使用由样本集形成的超球面描述,它主要由中心点a和半径R来定义。引入样本数据有效性隶属度si∈[ε,1],它表征了单样本xi在超球面内部的程度,si越大,说明越靠近样本点的中心,舰艇越不至于沉没。
引入非负标量松弛因子 ξi(i=1,2,…,N)表征测量错分程度的度量,所以siξi是对不同隶属度的样本错分程度的度量:隶属度大的错分支持向量,对优化函数的影响较大;反之,则影响较小,即隶属度越小的错分支持向量,在分类问题中被认为越不重要。根据SVDD的基本原理,可以通过下式的优化模型求解超球面中心点a和半径R。
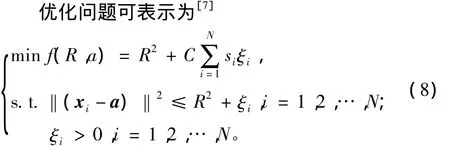
其中:‖·‖为欧式范数;C为常数,其作用为平衡超球面大小和异常值的数量,称为惩罚因子。

可由上式解出ai的值,再由式(10)得出球心a的坐标。可见,球心a实质上是xi的加权平均。值得提出的是,由上式解出来的αi的值,只有部分是大于0的,其他的均为0。
满足αi>0的αi对应的样本xi称为支持向量,用它们就可以进行超球面描述。支持向量可以分为2类,当αi=siC时,此时对应的数据点在超球面外部,也可能在超球面上;当0<αi<siC时,这些支持向量分布在超球面的边缘上。
球面半径R可通过求超球面上的点到球心的距离而得到。例如,设xi0为位于超球面上的点,则:
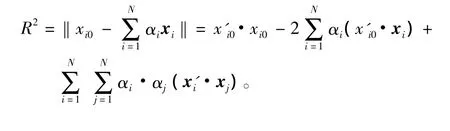
任一个破损模式对应的单指标向量集x,为了判别它是否在超球面内部,只需要计算数据到球心的距离。当此距离不超过半径R时,即认为该破损模式不会导致沉没;否则,则认为该破损模式会导致沉没。即,如果下式满足,则认为不会造成舰艇的沉没;否则,舰艇将会沉没。

上述介绍的方法仅涉及到数据所在空间的内积,也可以使用1个核函数K(·,·)代替上面的内积,这意味着将数据影射到1个高维特征空间,实现低维空间非线性问题向高维空间线性问题转化。
5 船模计算
使用第3.1节建立的水密区破损概率计算模型以及第4.2.2节的基于SVDD的沉没判据模型,对某船模在受到鱼雷攻击后的沉没概率进行计算。初始计算条件如下:
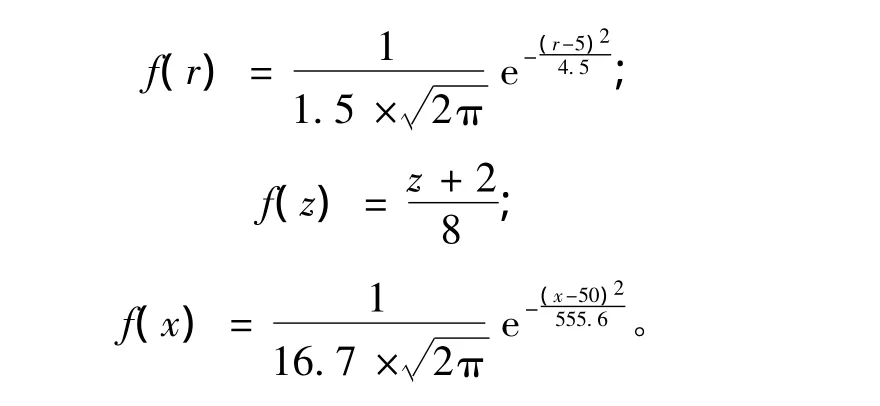
假设该鱼雷为接触爆炸,炸点的横向坐标在舷侧处,以概率1出现。
对多个设计方案进行仿真计算,沉没概率仿真计算结果如图2所示。其中,在使用基于SVDD沉没判别模型进行计算时,平均每次的识别时间为23 s。从测试的26个损伤模式来看,其识别结果与专家判别结果是完全一致的。

图2 沉没概率计算结果Fig.2 The calculation results of ship sinking probability
从图2可看出,方案1对应的沉没概率最小,为0.152,这也说明了其是最优的设计方案。
6 结语
介绍了一种计算舰艇沉没概率的解析模型,该模型可以避免以往仿真算法中收敛性难以确定和需要多次仿真计算的问题,大大提高了计算的精度,减少了计算的时间;实例计算也表明了该解析计算模型的可行性。
特别是建立了基于SVDD的沉没判据模型,该模型不仅避免了以往单指标判别的不客观性,还可以综合应用以往的专家判别知识,使用多指标综合的方法进行判别,具有较高的精度。
然而实际战损时,舰艇可能受到多种不同位置处的武器攻击,破损的水密区可能会不相邻。因此,如何建立存在不相邻水密区破损模式的沉没概率解析计算模型,依然是今后需要重点研究的问题。
[1]浦金云.舰艇生命力[M].北京:海潮出版社,2001.
[2]胡铁牛.货船概率破舱稳性计算及对分舱的影响[J].上海交通大学学报,1997,31(11):24 -29.
[3]GREENHORN J.The assessment of surface ship vulnerability to underwater attack[J].The Royal institution of Naval Architects,1988,3(1).
[4]姜礼平.工程数学[M].武汉:湖北科学技术出版社,2000.
[5]何汉林,魏汝祥.数值分析[M].武汉:湖北科学技术出版社,1999.
[6]TAX D,DUIN R.Data domain description by support vectors[C].Proceedings of ESANN99.Brussels:D.Facto Press,251 -256.
[7]TAX D,DUIN R.Support vector data description[J].Machine Learninig,2004(4):45 -66.
[8]李凌均,韩捷,等.支持向量数据描述用于机械设备状态评估研究[J].机械科学与技术,2005,24(12):1426-1429.
Ship sinking probability analytic calculation model
HOU Yue,PU Jin-yun,CHEN Xiao-hong
(Naval University of Engineering,Power College,Ship Safety Department,Wuhan 430033,China)
Factors that affect ship sinking probability calculation are analyzed and the analytic calculation model is given firstly.Watertight region damage probability calculation model and sinking judgmentmodel which are the two pivotal models of the analytic model are researched.Concerning the weapon blast point distribution is self-governed in three-dimensional direction;the analytic watertight region damage probability calculationmodel is founded.And then,ship sinking judgment indexes are analyzed and the sinking judgment arithmetic is founded based on support vector data description.At last the sinking probability of a ship model is calculated using the analytic calculation model and the results verified the correctness of the analytic model.
sinking probability;damage probability;analytic model;support vector data description;sinking judgment index
U674.71.01
A
1672-7649(2013)05-0065-04
10.3404/j.issn.1672-7649.2013.05.015
2011-06-13;
2012-12-06
侯岳(1988-),男,博士,主要研究方向为舰艇生命力评估。
