散货船的总振动模态计算和动力响应预报
2013-03-08夏利娟丁金鸿
陈 翔,夏利娟,丁金鸿,赵 党
(上海交通大学海洋工程国家重点实验室,上海 200240)
散货船的总振动模态计算和动力响应预报
陈 翔,夏利娟,丁金鸿,赵 党
(上海交通大学海洋工程国家重点实验室,上海 200240)
针对某散货船建立一维梁模型和混合有限元模型。在总振动计算的基础上,对3种不同的螺旋桨激振力的施加方式进行比较研究,计算其尾部及上层建筑的强迫振动响应,最后根据船舶振动基准进行振动评价。计算结果表明,该散货船的振动特性良好,对该类型船舶的振动和响应预报具有一定的参考价值。
散货船;总振动;激振力;混合有限元模型;强迫振动响应
0 引言
船舶在航行过程中,受到螺旋桨、主机和风浪等的激励作用,难免会发生振动。在船舶设计的初期,应考虑使船体固有频率与外界干扰力频率错开一定范围以避免发生共振。另外,船舶的上层建筑由于其自身的设计特点,比如高而短的外形、与机舱棚和烟囱分离的形式等,加之其靠近船舶的2个主要振源 (螺旋桨和主机),导致上层建筑结构更容易发生有害振动。当船舶振动水平超过一定数值时,会使船员感觉不舒适及某些精密仪器失灵。因此,有必要对尾部和上层建筑进行动力响应预报和评估。
船舶总振动的计算模型主要有一维梁模型、二维平面模型、整船三维模型和混合模型。综合考虑计算成本和计算精度,本文采用一维梁模型和混合有限元模型分别进行船舶总振动计算,采用混合有限元模型进行尾部和上层建筑的振动响应预报,并对结果进行了比较分析。在船舶振动响应计算时,要尽可能准确地模拟激振力。本文采用PCL编程真实模拟脉动压力沿船长的分布规律,并与常用的几种简化施加方式进行比较分析,获得了尾部及上层建筑的加速度响应值。在此基础上,根据ISO6954-1984船舶振动基准进行评价,结果表明,该散货船尾部及上层建筑的振动特性良好。
1 有限元模型
1.1 混合有限元模型的建立
沿船长方向自尾封板至第5货舱舱壁建立尾部三维有限元模型,如图1所示。板单元模拟甲板、外板、纵横舱壁及T型材腹板;梁单元模拟加强材、支柱及T型材面板;质量点单元模拟船员、船舶设备、货物、淡水、压载水等。

图1 散货船尾部三维结构示意图Fig.1 Schematic of the aft cabin
沿船长方向自第5货舱舱壁至首封板建立中首部一维梁模型,根据型线变化趋势将一维梁模型分为若干段等截面梁,每段梁的密度根据该段梁的质量和体积求得,剖面面积、垂向惯性矩、水平惯性矩取每段梁中间肋位的数值。
建立混合模型的关键问题之一在于尾部三维模型和中首部一维梁模型之间的连接。目前较常用的有以下2种连接方法[3]:
1)连接处选在船体横剖面刚度较大的剖面处(如横舱壁),将船体梁模型中位于连接剖面处的节点定为主节点,将三维模型中位于连接截面处的所有节点定为从节点,并规定主从节点的位移和转角相同,以保证连接处的变形一致;
2)尾部三维模型与船体梁模型之间用适当刚度的联结梁连接,以保证该连接处变形协调。
本文采用第2种连接方法,连接梁的弹性模量约为实际材料的10倍左右,其剖面属性取自相邻的一维梁单元,密度为0。船体梁的高度与第5货舱舱壁区域的中和轴高度一致。
采用MSC/Patran软件建立的混合有限元模型如图2所示,取OXYZ右手直角坐标系,坐标原点位于基线FR0处,X轴沿基线指向船首方向,Y轴沿船宽方向,Z轴沿船高方向。
1.2 附连水质量的计算
当船舶振动时,周围的水也随之运动,这部分水的质量相当于增加了船体梁的质量,称为附连水质量,它对船体梁振动影响较大。本文采用刘易斯图谱法进行附连水质量的计算。
垂向振动各阶附连水质量及水平振动各阶附连水质量计算公式如下[1]:

式中:Ki为三维流动修正系数,取决于船长和船宽之比 (垂向振动)或船长和吃水之比 (水平振动)以及振动的阶数;Cv和Ch分别表示附连水质量系数,取决于剖面形状及宽度吃水比。
经计算,该散货船在满载工况下的前5阶附连水质量数值如表1所示。

表1 前5阶附连水质量 (单位:t)Tab.1 Added watermass of five-order vibration
对于尾部三维模型,附连水质量采用质量点单元来模拟,施加在水线以下的所有外板节点上;对于一维梁模型,附连水质量则以非结构质量的形式施加在梁单元上。
2 总振动分析
为了获得全船总体的振动特性,需要对船舶进行模态分析。本文分别采用一维梁模型和混合有限元模型,针对满载工况进行了模态分析,获得前3阶固有频率及振型。计算结果如表2所示。
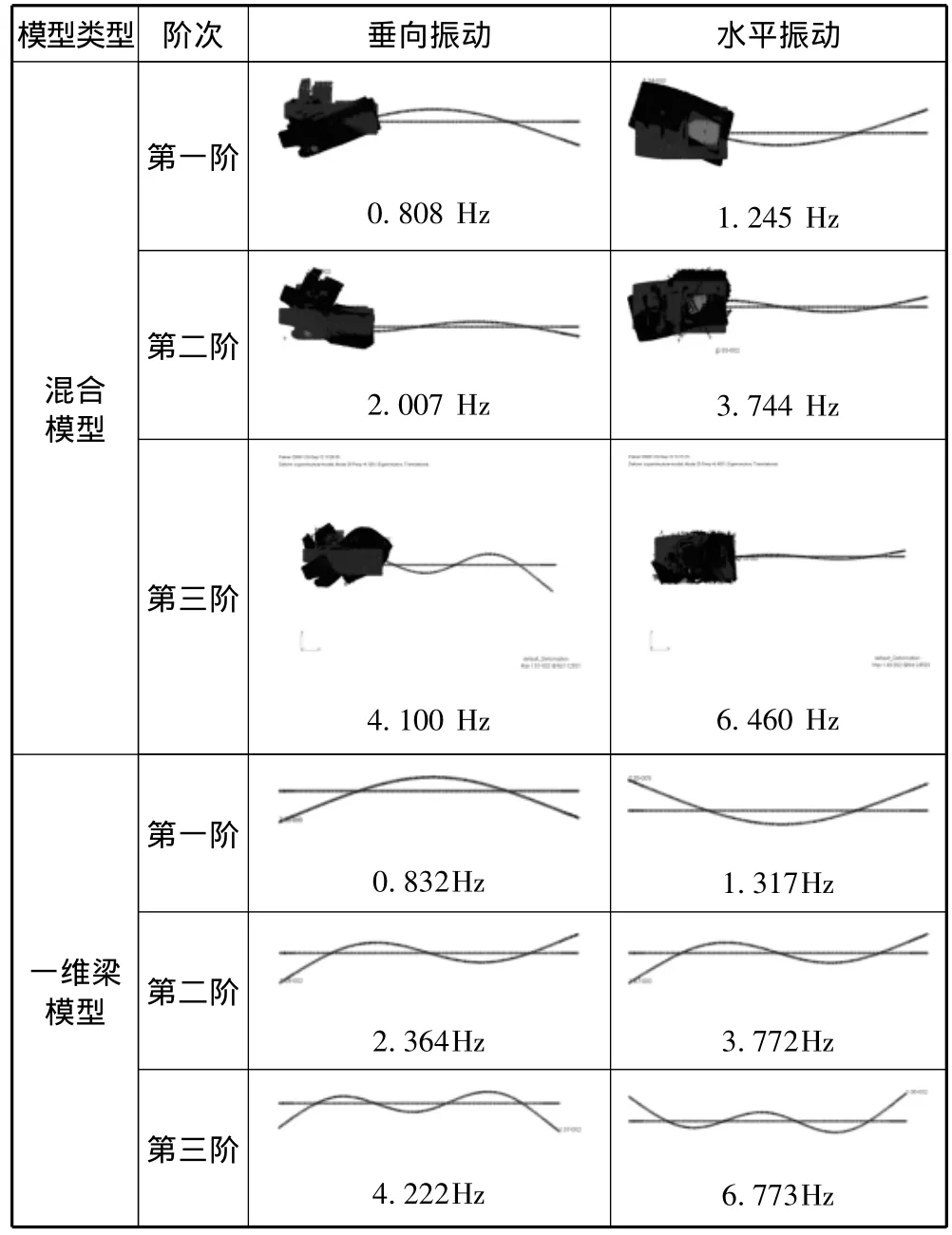
表2 前3阶固有频率及振型Tab.2 Natural frequency and mode of three-order vibration
本船螺旋桨转速为119.7 r/min,叶片数为4,故螺旋桨激励频率为7.980 Hz。由表2可知,前3阶垂向和水平固有频率与螺旋桨叶频错开较远,满足频率储备要求,引发船体低阶共振的可能性不大。
3 频率响应分析
3.1 激振力的计算
采用有限元法计算船舶结构振动响应时,准确地施加各种激振力是计算的关键。引起船体尾部振动的振源很多,主要有螺旋桨、主机、船舶辅机设备和波浪等,本文仅考虑螺旋桨激振力。
估算螺旋桨激振力的方法主要有3种[1]:模型试验、经验公式和理论计算。估算螺旋桨激振力的经验公式有2种形式,一种以脉动压力形式给出,一种以表面力形式给出。
3.1.1 脉动压力的计算
当螺旋桨资料有限时,通常采用霍尔顿法计算脉动压力。
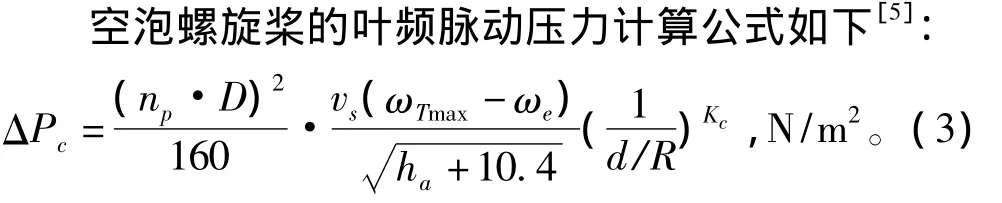
式中:np为螺旋桨转速,r/min;D和R分别为螺旋桨直径和半径,m;vs为航速,m/s;ha为桨轴中心线的水下沉深,m;d为当桨叶在顶点位置时,桨上0.9R处到浸在水中的船壳的距离,m;Kc为与d/R有关的系数。当d/R<1.0时,Kc=1.7-0.7d/R;当d/R≥1.0时,Kc=1。

计算出的该散货船螺旋桨脉动压力的数值见表3。
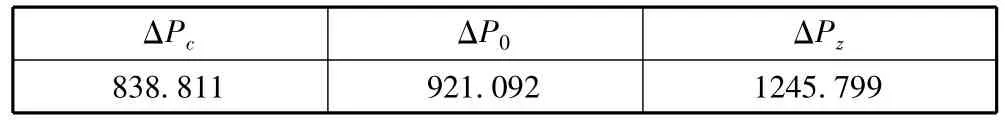
表3 满载状态下螺旋桨脉动压力 (单位:N/m2)Tab.3 Propeller pressure pulse in full load condition
3.1.2 脉动压力 (表面力)的施加
螺旋桨脉动压力沿船长的分布规律为从尾部开始向首部方向,压力逐步升高,在桨盘面前方约0.1倍的螺旋桨直径处,脉动压力达最大值,然后向首部迅速减小。
本文采用3种方案实现脉动压力(表面力)的施加:
方案1:螺旋桨脉动压力的施加范围只考虑螺旋桨上方约为螺旋桨直径D*D的面积,其大小等于由霍尔顿法算得的总脉动压力的幅值。螺旋桨脉动压力分布示意图如图3所示。

图3 螺旋桨脉动压力的分布示意图 (方案1)Fig.3 Schematic of propeller pressure pulse distribution(method 1)
方案2:沿船体表面对脉动压力的积分得到螺旋桨对船体的总激振力称为表面力,其值可按式(6)计算。其中P为作用于浸水船体表面的总压力脉动值,作用点为螺旋桨中心正上方的船体外板节点。

方案3:根据螺旋桨脉动压力沿船长的分布规律,通过PCL编程建立相关函数,脉动压力的作用区为:纵向从尾封板起延伸到靠近船首一侧距螺旋桨盘面3倍螺旋桨直径处,垂向为设计水线以下的船体表面。
其步骤为:编写PCL函数pressure_pulse(如图4所示),以此函数为标量函数创建标量型空间场pressure_pulse,将此空间场施加到脉动压力的作用区域。
根据以上步骤得到的脉动压力分布图如图5所示。

图4 编辑pressre_pulse函数示意图Fig.4 Schematic of the pressure pulse function

图5 螺旋桨脉动压力的分布示意图 (方案3)Fig.5 Schematic of propeller pressure pulse distribution(method 3)
3.2 响应计算点的选取
根据船上振动控制指南[5],本文分别选取了主甲板与尾封板的交线、螺旋桨附近、A甲板、B甲板、C甲板、桥楼甲板、罗经甲板和烟囱上的若干点作为计算点,每个点的计算结果取该点和与之相邻若干点的加速度响应的最大值。各计算点的位置如图6~图11编号所示。
图6 尾部甲板和螺旋桨附近计算点Fig.6 The calculation points on aft deck and near propeller
图7 A甲板计算点Fig.7 Calculation points on A deck
图8 B甲板计算点Fig.8 Calculation points on B deck
图9 C甲板计算点Fig.9 Calculation points on C deck

图10 桥楼甲板计算点Fig.10 Calculation points on bridge deck

图11 罗经甲板和烟囱处计算点Fig.11 Calculation points on compass deck and funnel roof
3.3 响应计算结果
本文采用模态叠加法进行频率响应计算,频率范围取为0~20 Hz,螺旋桨激振力采用上述3种方案予以施加,模态阻尼参考ABS的振动指南[9]取值为0.015。计算结果如表4。

表4 满载工况下各响应计算点的加速度响应值 (单位:m2/s)Tab.4 Acceleration responses of each calculation points on full load condition
由表4可知,和方案1与方案2这两种简化方法相比,方案3的响应计算值相对较大,且与方案2的响应计算值相对比较接近。尤其是在较高的桥楼甲板和罗经甲板等部位,方案3的响应计算值有较为明显的增加。由此可见,脉动压力的施加方法对计算结果有一定影响。
以上3种方案各有优缺点,方案1和方案2采用简化方法,载荷施加方便;方案3需要PCL编程实现,能较准确地根据经验公式模拟螺旋桨附近的脉动压力分布。可根据实际工程精度的要求选择合适的施加方案,但从准确模拟脉动压力分布的角度出发,本文推荐采用方案3实现脉动压力的施加。
3.4 变转速下的频响分析
为了获得较宽频率范围内的振动响应规律,本文取转速的60%~110%MCR进行计算,在非最高转速下,螺旋桨与转速的关系为三次方关系[1],即:

由此算出螺旋桨在70~124 r/min之间所有转速下的螺旋桨激振力,阻尼仍取0.015。计算节点选取振动响应较大的甲板纵中剖面尾端(Node35804)和烟囱顶端(Node75147),计算结果如图12所示。
由图12可知,甲板纵中剖面尾端分别在7.13 Hz和8.02 Hz有较大的响应峰值55.7 m2/s和77.4 m2/s;烟囱顶端分别在7.15 Hz和8.05 Hz有较大的响应峰值48.6 m2/s和71.2 m2/s。以上两频率对应的转速大约在107 r/min和120 r/min,选择转速时应尽量避开这2个值以取得较好的航行环境。
3.5 振动评估
由动力响应计算结果(表4)可知,A,B,C甲板的最大响应值分别为28.6,34.8和43.2 m2/s,桥楼甲板和罗经甲板的最大响应值分别为49.3 m2/s和51.5 m2/s,尾部和烟囱的最大响应值分别为75.4 m2/s和63.6 m2/s。根据商船振动的综合评价基准ISO6954-1984[8],该散货船的响应值均处于不可能有害区,发生有害振动的可能性不大。
4 结语
本文建立了某散货船的一维梁模型和混合有限元模型,进行全船总振动分析,在此基础上采用模态叠加法对混合有限元模型进行尾部和上层建筑的振动响应计算。脉动压力的计算和施加是动力响应计算的关键问题之一,本文针对3种不同的施加方案,分别进行比较研究和优劣分析,并推荐采用方案3实现脉动压力的准确施加。最终实现了对该散货船的总振动和动力响应评估。
[1]金咸定,夏利娟.船体振动学[M].上海:上海交通大学出版社,2011.
[2]何友声,王国强.螺旋桨激振力[M].上海:上海交通大学出版社,1987.
[3]吴梵,郭日修.舰船尾部振动分析整船混合有限元模型的集成方法研究[J].海军工程学院学报,1999(4):103-107.
WU Fan,GUO Ri-xiu.An integration method of hybrid F.E.models of ship-hull in calculating the after-body vibration of ships[J].Journal of Naval University of Engineering,1999(4):103 -107.
[4]夏利娟,吴卫国,翁长俭,等.混合有限元模型的集成方法[J].上海交通大学学报,2001,35(4):544 -547.
XIA Li-juan,WU Wei-guo,WENG Chang-jian,et al.Integration methods on mixed FEM model[J].Journal of Shanghai Jiaotong University,2001,35(4):544 -547.
[5]中国船级社.船上振动控制指南[S].北京:人民交通出版社,2000.
[6]吴嘉蒙.2750TEU集装箱船的全船总振动评估[J].船舶,2008(2):45-50.
WU Jia-meng.Evaluation on global vibration analysis on a 2750 TEU container vessel[J].Ship & Boat,2008(2):45-50.
[7]吴嘉蒙,陈曙梅.2750TEU集装箱船的局部振动评估[J].船舶,2008(5):10 -16.
WU Jia-meng,CHEN Shu-mei.Evaluations on local vibration analysis on a 2 750 TEU container vessel[J].Ship & Boat,2008(5):10 -16.
[8]International Standard ISO 6954.Mechanical vibration and shock-Guidelines for overall evaluation of vibration in merchant ships[S].Edition 1984.
[9]ABS.Guidance notes on ship vibration[S].2006.
[10]MSC.Software Corporation.PCL and Customization[M].2003.
[11]MSC.Software Corporation.PCL Reference Manual[M].2003.
The global vibration and dynam ic response evaluation of a bulk carrier
CHEN Xiang,XIA Li-juan,DING Jin-hong,ZHAO Dang
(State Key Laboratory of Ocean Engineering,Shanghai Jiaotong University,Shanghai,200240)
This paper constructed a bulk carrier's 1D beam model and mixed finite elementmodel.Basing on the global vibration analysis,we compared and researched three different methods of adding propeller exciting force,calculated the forced vibration response of the aft structures and the superstructure,and then evaluated the vibration level.The results indicate the vibration characteristic of the bulk carrier is satisfying.This paper is valuable for the evaluation on vibration and response analysis of bulk carriers.
bulk carrier;global vibration;exciting force;mixed finite elementmodel;forced vibration response
U674.13+4
A
1672-7649(2013)03-0115-06
10.3404/j.issn.1672-7649.2013.03.026
2012-09-27;
2012-12-31
国家自然科学基金资助项目(50909060);海洋工程国家重点实验室青年创新基金资助项目
陈翔(1987-),男,硕士研究生,主要从事船舶结构振动及优化研究。
