基坑土钉支护的非线性有限元分析

2013-03-06王海波秦皇岛市规划设计研究院066001

河南建材 2013年2期

王海波秦皇岛市规划设计研究院（066001）

0 引言

土钉墙是一种基于土体自身承载能力的挡土结构，相对于其它支护形式，土钉墙的支护机理是通过对控制被加固土体的变形，实现土体的稳定。土钉墙是通过将外裹水泥砂浆的钢筋以一定间距置入土体，并在土坡表面喷射混凝土形成混凝土面层，实现对土体的加固[1]。

土钉墙支护的计算方法主要有传统的极限平衡分析法和近年来发展较快的有限元法。极限平衡分析法具有概念明晰、计算简单、应用广泛的优点，但是无法计算支护结构的变形[2]。利用计算机技术的有限元法,不仅可以计算支护结构的内力与变形，还可以考虑土体的本构关系和非均匀性、各向异性等特性，对施工过程进行模拟，计算精度较高。

1 土钉墙的有限元分析

1.1 土钉墙的构造

土钉墙支护是在原位土体中按照一定长度和密度置入注浆钢筋或钢管作为土钉，通过土钉与土体的相互作用弥补土体自身强度的不足，在开挖面上设置钢筋网并喷射混凝土形成面层或者设置预制混凝土面板，以进一步限制土体的变形，保持开挖面后土体的整体稳定性。这种由原位土体、土钉、钢筋混凝土面层三部分组成的支护结构体系即为土钉墙支护[3]。相对于钢筋混凝土桩、地下连续墙等被动受力支护结构,土钉墙是一种主动加固技术，能有效的发挥土体自身的强度。

1.2 土钉墙的有限元模型

目前在工程界应用广泛的土体本构模型有DP模型和M-C模型。但空间状态的M-C模型屈服面具有角隅性质，不利于数值分析。D-P模型则对此进行了改进，使模型屈服面光滑，同时考虑了岩土材料的剪胀性和扩容性。分析选用D-P模型，屈服表达式为:

式中:F为屈服函数，I1为应力张量第一不变量，J2为应力偏量第二不变量，α、K为D-P模型常数。

在结构的有限元分析中，基于土钉墙结构的自身特点，可将土钉墙的有限元计算简化为平面应变问题。构建土钉墙结构的有限元模型时，采用弹塑性D-P模型的基坑土体采用四节点等单元，土钉采用弹性杆单元，仅受轴力作用，喷射混凝土面层简化为弹性梁，受弯矩和剪力的作用。为了提高计算精度，更真实的模拟实际受力情况，在土钉墙结构（土钉与混凝土面层）与土体之间设置了接触面单元，以模拟结构的接触行为。

1.3 接触面单元

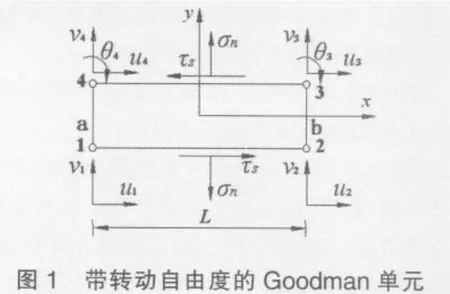
土体和支护结构之间的相互作用是一种接触行为，很多情况下，这种接触行为会产生土体和支护结构之间的相对位移，为了更好的模拟这种接触行为,可以在土体和支护结构之间设置接触面单元。工程中应用广泛的为无厚度接触面单元，采用带转动自由度的Goodman无厚度接触面单元，如图1所示。接触面单元由接触面1-2和3-4组成，初始状态下，两接触面完全吻合，厚度为0；受力变形后，利用3-4边与1-2边的相对位移，来模拟接触面产生的拉裂、错位。