特高含水期剩余油孔道选择微观机理研究

进入特高含水期，由于含水率上升，油田大部分区域遭到水淹，剩余油由中低含水期的连片状变为高度分散状，越到含水开发后期，微观因素影响越显著。有学者［1］认为：由于微观因素的影响，有大概60%～70%左右的剩余油残留在油藏中，而且水驱开发油田特高含水期剩余油分布具有高度分散特性。目前，中国大多数陆上油田均进入高含水甚至特高含水期，但采收率仅30%左右。因而，为了提高采收率保持油田稳产，关于特高含水期剩余油相关研究迫在眉睫。2012年，刘志斌 （Liu Z B）等［2］建立了高含水期两相渗流区饱和度分布方程，描绘了不同时间不同渗流区域的饱和度变化规律。除此之外，还有许多学者［3～5］对特高含水期剩余油饱和度分布及剩余油开发技术进行了研究，但关于特高含水期剩余油微观渗流机理研究较为少见。特高含水期剩余油滴孔道选择微观机理研究对提高采收率，保持油田稳产和高产意义重大。笔者将以孔隙网络模型中的剩余油滴为研究对象，研究特高含水期剩余油滴孔道选择微观机理。孔隙网络模型将多孔介质抽象为理想的几何形状，复杂的孔隙空间由相互连通的喉道和孔隙组成。1956年，Fatt［6］最先提出了网络模型表示孔隙结构特征。1989年至1991年，Dullien等［7，8］完善了Fatt的孔隙模型。1991年Blunt等［9］和 Goode［10］开展了孔隙网络模拟实验［9，10］。1991年至2008年间，Vizika等［11～16］研究发现两相渗流状态不仅受孔隙空间特殊性质的影响，而且受到毛细管力、黏度比、黏滞力、重力、浮力等微观因素的影响。笔者将综合考虑特高含水期孔隙网络中各种微观力对剩余油滴的作用，同时将明确剩余油滴孔道选择的机理。

1 假设条件

笔者所做分析基于如下假设：①油滴不破裂；②孔隙中油滴半径大于毛细管孔道半径；③忽略非均质性的影响；④孔隙中油滴渗流为径向流。

2 油滴微观受力状态分析

特高含水期剩余油呈分散状，多以水包油性质的油滴存在，微观受力影响较大，因而重力、浮力、毛细管效应阻力及摩擦力的作用不能被忽略。除了注入水驱替力，特高含水期剩余油油滴还受到下列力的作用：重力、浮力、楔压效应阻力、滞后效应阻力、贾敏效应阻力、摩擦力、黏滞力。下面对特高含水期孔隙网络模型中油滴的微观受力状态进行分析。

2．1 浮力与重力

水包油滴所受重力与浮力的合力为：

式中：F0为浮力，N；G 为重力，N；ρw、ρo分别为水和油的密度，g／cm3；Vo为油滴的体积，cm3；So为油滴的表面积，cm2；g为重力加速度，9．8m／s2。

若ρw＞ρo，则F0－G＞0，合力方向向上，在此力的作用下，油滴向上运移；若ρw＜ρo，则F0－G＜0，合力方向向下，在此力的作用下，油滴向下运移。

2．2 液阻效应阻力

当油滴半径大于毛细管孔道半径，油滴流经毛细孔时会产生阻碍作用，这种作用力称为液阻效应阻力。其计算公式为：

式中：pc为贾敏效应阻力，MPa；R为毛细管半径，μm；σ为界面张力，mN／m；r为孔隙半径，μm；θ为润湿角，（°）。

2．3 楔压效应阻力

对于等径毛细管，液滴静止，由于存在柱面和球面毛细管力，因而会产生一种阻力效应：这个阻力为液滴球形和柱形界面在垂直管壁方向产生的毛细管力的合力。其计算公式为：

式中：pⅠ为楔压效应阻力，MPa。该力的作用使得珠泡在管壁的附着程度增加。

2．4 滞后效应阻力

对于等径毛细管，液滴运动，由于其两端球面毛细管力不等，因而会产生滞后效应。该力为液滴两端球形界面毛细管力的合力，其方向与液滴运动方向相反，计算公式为：

式中：pⅡ为滞后效应阻力，MPa。该力作用是阻碍珠泡向前运动。

2．5 流体与岩石的摩擦阻力

如果两表面互为静止，那么在两表面间接触的地方会形成一个强结合力——静摩擦力，除非破坏了这个结合力才能使一表面相对另一表面运动，该强结合力与作用在其一表面上的垂直力之比值叫做静摩擦系数μs。计算公式为：

在流体流动后，过些时候速度会减慢最后静止，这表示流体流动时，它的表面和另一表面，如岩石或者另一种流体，仍然存在动摩擦力。计算公式为：

式中：Fs、Fd分别为静摩擦力和动摩擦力，MPa；N 为支持力，MPa；μs、μd分别为静摩擦系数和动摩擦系数。

2．6 黏滞力与剪切应力

黏滞力是由流体分子间相互摩擦造成的，任何流体流动都会有黏滞力产生，它始终是流动的阻力。黏滞力存在的前提是流体发生运移，它对流体的渗流速度产生影响。

3 油滴综合受力方程

此处，选择一微观孔隙结构单元 （图1），研究特高含水期孔隙网络模型中油滴的综合受力方程。

如图1所示，1、2、3分别代表3个不同的油层，油滴所在孔隙记为A。a、b、c、d分别代表4根不同的毛细管，其中a、b两根毛细管为第2层平面上的两根毛细管，c、d分别为第1～2层和第2～3层垂向毛细管，4根毛细管分别代表4个不同的方向。图1中油滴在4根不同的毛细管中均受到不同微观力的作用，不妨设4根毛细管的毛细管半径分别为ra、rb、rc、rd（单位为μm），油滴选择它们时对应的合力分别为Fa、Fb、Fc、Fd（单位为 MPa）。不同的毛细管半径对应的微观力不同。

对于图1中第2层a、b两根毛细管，受地层倾角的影响，油滴选择这两根毛细管，通过其狭窄孔道时，会产生液阻效应阻力，设两毛细管摩擦系数相同；若摩擦系数不同则需重新讨论摩擦力的变化情况。

1）当浮力作用大于重力作用时，油滴所受阻力为楔压效应阻力、重力浮力的分力产生的摩擦力和液阻效应阻力，动力为注入水驱替力和重力浮力沿运动方向上的分力，总合力为：

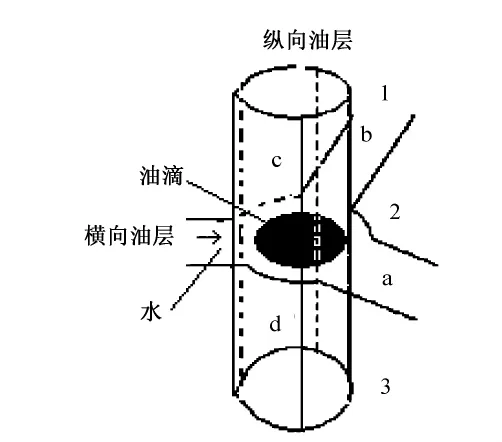
图1 层间微观孔隙结构单元

式中：Δp为注入水驱替力，MPa；α为地层倾角，（°）；θ2、θ1分别为前、后端润湿角，（°）；r为孔隙A 的半径，μm。

2）当浮力作用小于重力作用时，油滴所受阻力为重力浮力的分力及其与楔压效应阻力一起产生的摩擦力和液阻效应阻力，动力为注入水驱替力，总合力为：

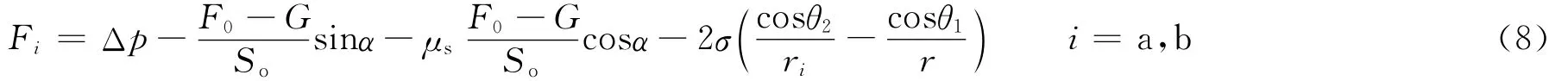
若大毛细管为某一孔隙，此时除了孔道半径外，孔喉比ri／r也直接影响油滴的综合受力。当驱替压力能克服油滴作功时，油滴运动时还必须克服黏滞阻力的作用，因而在研究油滴运动状态时需要综合考虑黏滞力的作用。

1）当浮力作用大于重力作用时，所受合力为：

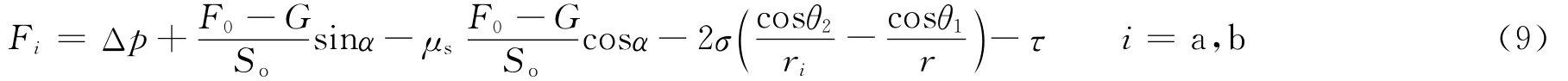
式中：τ为单位面积上的黏滞力，MPa。

2）当浮力作用小于重力作用时，所受合力为：

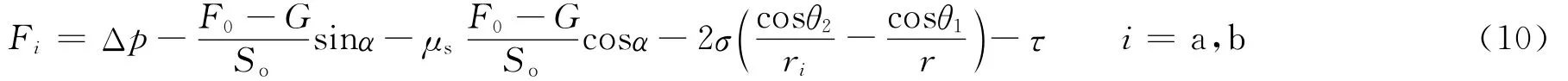
因而黏滞力直接影响到油滴的运移速度，对于剩余油滴的运动状态本文不作深入研究。

对于c、d两根毛细管，由于处于垂直方向，因而受重力与浮力的作用更显著，同时会受到毛细管效应力、摩擦力的作用，当作用在油滴上的动力克服阻力作功时，油滴还会受到黏滞阻力的作用。

1）当浮力作用大于重力作用时，c管油滴所受阻力为楔压效应阻力产生的摩擦力和液阻效应阻力，动力为浮力与重力的差，总合力为：

2）当浮力作用小于重力作用时，d管油滴所受阻力为楔压效应阻力产生的摩擦力和液阻效应阻力，动力为重力与浮力的差，总合力为：

4 特高含水期油滴孔道选择微观机理

4．1 微观孔道选择机理定性描述

1）当油滴在4根毛细管中的某一个合力分别大于其他各个合力时，油滴选择该合力所在的孔道。也即（式中反斜杠“＼”表示除去的意思）时，油滴优先选择合力F所在毛细管。

2）当油滴在4根毛细管中的某2个合力相等且分别大于油滴在其他毛细管的合力时，需要进行讨论：若此时两者相等，则油滴被卡在这2根毛细管与孔隙中；若两者不等，油滴选择合力大的孔道进行运移。也时，分两种情况讨论：①油滴运移出其他2根毛细管后，仍然有F1＝F2，此时油滴富集在F1、F2对应毛细管和孔隙连接处；②油滴运移出其他2根毛细管后，F1≠F2，则油滴选择合力大的孔道在该合力作用下进行渗流。

3）当油滴在4根毛细管中的某3个合力相等且大于油滴在余下毛细管的合力时，需要进行讨论：若此时三者相等，则油滴被卡在这3根毛细管与孔隙中；若三者不等，则油滴选择合力大的孔道进行渗流。

4）当油滴在4根毛细管中的合力均相等，此时油滴被卡在4个孔道和孔隙中。

4．2 微观孔道选择机理定量研究

由特高含水期孔隙网络模型中油滴综合受力方程知：当浮力大于重力作用时，油滴倾向于选择a、b、c毛细管；当浮力小于重力作用时，油滴倾向于选择a、b、d毛细管。因而孔道选择实质为3种作用力下的选择。

浮力作用大于重力作用时，c管油滴所受阻力为液阻效应阻力，动力为浮力与重力的差，总合力为：

当油滴完全进入c管时，c管油滴所受阻力为楔压效应阻力引起的摩擦力和液阻效应阻力，动力为浮力与重力的差，总合力为：

a、b两根毛细管油滴所受阻力为重力、浮力的分力产生的摩擦力和液阻效应阻力，动力为注入水驱替力和重力、浮力沿运动方向上的分力，总合力为：

1）当3根毛细管半径均相等时，此时Fa＝Fb，因而 只需讨论Fa＝Fb与Fc的关系即可。Fa－Fc＝时，油滴会滞留在孔隙A与a、b毛

2）当a、b、c毛细管半径不全相等时：①若Fa＝Fb＝Fc，即当驱替压力满足时，油滴滞留在孔隙A与a、b、c毛细管构成的共同区域内。②若Fa＝Fb＞F，c此时ra＝rb，因而只需讨论a或b毛细管与c毛细管的关系：说明油滴选择孔道时与油滴在孔隙中的润湿角无关，只与油滴在孔道中的前端润湿角时，油滴会滞留在孔隙A与毛细管a、b共同围成的区域内；当时，油滴会选择c毛细管进入。③ 若F，因而只需讨论Fba与Fc的大小关系，最终确定油滴对孔道的选择：若则此时油滴选择a毛细管进入；若则此时油滴选择c毛细管进入。

对于浮力小于重力作用时，可以仿上面理论对a、b、d毛细管进行讨论，确定油滴对孔道的选择机理。

若孔隙A处油滴最终选择a毛细管，油滴一部分进入a毛细管，此时合力：

当油滴在全部进入a毛细管，此时还需考虑楔压效应阻力差生的摩擦力的作用，此时合力为：

若给定Δp＝0．03MPa，ro＝300μm，r＝500μm，σ＝25mN／m，μs＝25mN／m，θ1＝π／3，θ2＝π／6，地层倾角α＝21°，则可以拟合出油滴所受合力随毛细管a孔道半径ra变化关系曲线，见图2。

图2 毛细管半径与油滴所受合力关系曲线

5 结论

1）特高含水期剩余油多呈分散油滴状，重力、浮力、毛细管效应力及摩擦力的作用不能被忽略；

2）研究油滴的影响因素，建立了孔道半径与剩余油滴微观受力关系方程；

3）以油滴受力关系方程为基础研究了剩余油滴孔道选择机理。

［1］刘宝珺，谢俊，张金亮 ．剩余油技术研究现状与进展 ［J］．西北地质 ，2004，37（4）：1～6．

［2］Liu Z B，Liu H H，Ding X F．Theoretical study of water saturation with percolation mechanics method ［J］．Open Petrol Eng J，2012，5：21～25．

［3］李中风，何顺初，杨文新 ．微观物理模拟水驱油实验及残余油分布分形特征研究 ［J］．中国石油大学学报 （自然科学版），2006，30 （3）：67～71．

［4］王朴，蔡进功，谢忠怀 ．用含油薄片研究剩余油微观分布特征 ［J］．油气地质与采收率，2002，9（1）：60～61．

［5］徐守余，朱连章，王德军 ．应用方针理论研究剩余油的形成与分布 ［J］．石油学报，2005，26（2）：69～72．

［6］Fatt I．The network model of porous media：Capillary pressure characteristic ［J］．Trans AIME，1956，107 （1）：144～159．

［7］Dullien F A，Zarcone I F，Macdonald A C．The effects of surface－roughness on the capillary－pressure curves and the heights of capillary rise in glass bead packs ［J］．J Colloid Inerf Sci，1989，278 （1）：362～372．

［8］Dullien F A，Francis S，Kai Y．Hydraulic continuity of residual wetting phase in porous media ［J］．J Colloid Inerf Sci，1986，109（1）：201～218．

［9］Blunt M，King P．Relative permeabilities from two and three dimensional pore－scale network modeling ［J］．Transport Porous Med，1991，6 （4）：407～433．

［10］Goode P A，Ramakrishnan T S．Momentum transfer across fluid－fluid inerfaces in porous media：A network model ［J］．AICHE J，1993，39 （7）：1124～1993．

［11］Vizika O，Avraam D G，Payatakes A C．On the role of the viscosity ratio during low－capillary number forced imbibitions in porous media ［J］．J Colloid Inerf Sci，1994，278 （165）：386．

［12］Hughes R G，Blunt M J．Pore scale modeling of rate effects in imbibition ［J］．Transport Porous Med，2000，40 （3）：295．

［13］Singh M，Mani V，Honarpour M M，et al．Comparison of viscous and gravity dominated gas－oil relative permeabilities ［J］．J Petrol Sci Eng，2001，30 （2）：67～81．

［14］Tsakiroglou C D，Theodoropoulou M，Karoutsos V．Non－equilibrium capillary pressure and relative permeability curves of porous media ［J］．AICHE J，2003，49：2472～2486．

［15］Tsakiroglou C D，Theodoropoulou M，Karoutsos V，et al．Determination of the effective transport coefficients of pore networks from transient immiscible and miscible displacement experiments ［J］．Water Resour Res J，2005，41 （2）：1029～1031．

［16］Theodoropoulou M A，Sygouni V，Karoutsos V，et al．Relative permeability and capillary pressure functions of porous media as related to the displacement growth pattern ［J］．Int J Multiphas Flow，2008，31 （10－11）：1155～1190．