基于仿真方法的钢构件生产制造的成本优化

董晓宇 张艺霞

安阳工学院（455000）

0 引言

对于一个钢构厂来讲，是在生产计划的管理体系下运行的，生产计划作为合同计划部分和各工序生产计划编制之间的纽带,起着举足轻重的作用。生产计划既是上层合同计划管理部分产生的结果，又是下面生产工序编制生产作业计划的数据来源，合同计划部分根据整个生产线的情况统筹优化安排而生成各工序的生产计划，同时各工序的生产计划编制按照生产计划的要求，在生产计划范围内编制各工序的生产作业计划，以达到全局优化条件下的局部优化。钢构件生产安排计划是否合理可以体现一个钢构件生产厂家的生产能力，既一年内能生产出来产品的数量。如对于一批钢构件，车间不同工种工人的数量及其协作能力，有其不同的反映生产能力的指标。

仿真的第一步就是建立模型。传统仿真技术中,一个仿真系统要首先建立起系统的数学模型——一次仿真模型，然后再改写成适合计算机处理的形式——仿真模型。仿真模型可以说是系统的二次近似模型。建立起仿真模型后，才能书写相应的程序。仿真基本上是一种通过实验来求解的技术。通过仿真实验要了解系统中变量之间的关系，要观察系统模型变量变化的全过程，此外，为了对仿真模型进行深入研究和结果优化，还必须进行多次运行、优化等工作，因此，良好的人机交互性是系统仿真的一个重要特性[1]。

1 钢构件生产工序仿真建模及成本优化

1.1 问题系统分析

因为一个厂家有其最大生产能力的限制，所以这是一个复杂的有限元排队系统。所谓有限元排队系统是指在系统中只有优先个顾客,譬如m个,一旦系统中已有m个顾客,就不会再有新的顾客到达。这个系统包括顾客到达、顾客等待、服务台服务及顾客离去等活动。顾客即构件原材料是成批到达的，每批到达的顾客数是随机的，每批顾客相继到达的时间间隔也是随机的。如一个钢构厂有很多分厂，安排生产的人员可凭经验将产品分给不同的分厂进行加工，影响了到达特定厂家的顾客数及每批到达的时间间隔。顾客接受服务的时间也是随机的，主要受构建种类、加工工艺及工人熟练程度的影响。从理论上讲，在构件生产过程中当前工序完成之后才可进行下一道工序的操作。因此，这个系统可归结为一个多级串并联、参数可变、即消失又等待的混合随机服务系统。如图1所示。

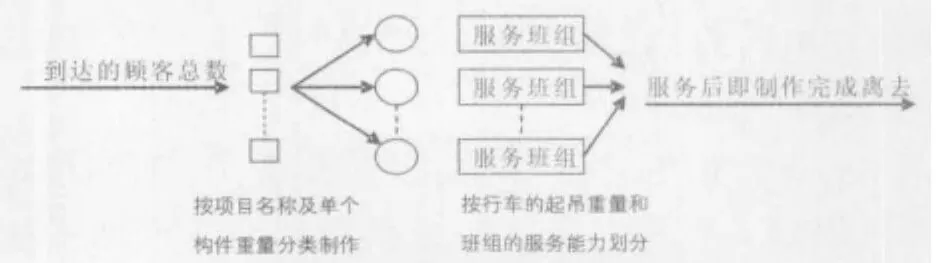
图1 服务系统示意图

1.2 仿真模型的构造

1.2.1 统计数据处理

对与钢构件生产相关随机因素的分析，可以对生产厂家历史数据经统计检验确定其概率分布。

1）构件数量都是成批到达的，但是每批顾客中的构件数量q（一般以千吨为单位）是不同的。分到一个工程加工的时候,工厂的容量上限Q是一定的,如果q≤Q，进入系统开始等待，否则选择离去，既分到其他厂房加工。当构件到厂之后，因为工厂月生产量变化不大，如按天或月计算，可视为平均到达，到达的概率皆视为1。

2）构件相继到达的时间间隔。生产准备部安排生产的过程中保证厂中时时有活干得原则下，统筹安排原材料进厂,但是实际原材料进厂是随机的，为了方便计算我们视为按泊松流到达，相继到达时间间隔服从负指数分布。由于季节和是否再签订新的合同的变化而使得安排的生产量有所差异。在各时间区内认为顾客流的强度不变。经统计，不同季节不同月份相继顾客到达的间隔时间的平均值 （天）为:

表1 不同月份相继顾客到达统计表

如在夏季或冬季,还有法定假期等因素的影响，安排生产，即材料到达工厂的时间会延长。但当舒适的季节来临生产安排紧凑，即材料到产时间间隔会缩短。因此，二者都不考虑，作近似抵消。

3）材料进厂后等待加工的时间。原材料进厂后等待的时间也是随机的，由于条件限制我们暂时以正态分布来说明，给定不同月份等待时间的平均值μ和均方差σ。实际的情况，我们要根据具体数值的统计检验来获得等待时间的平均值μ与均方差σ。

4）材料进厂开始加工制作的时间，既顾客接受服务的时间。顾客接受服务的时间是随机的，不仅是顾客数，即一批材料中加工的量不同，即使是同样的吨位也会因为加工工艺和设计图纸的不同而不同。据初步统计检验，材料的加工时间服从正态分布,不同的加工量的加工时间的平均值设为μ1，均方差设为σ1。

5）材料加工过程中的加工制作费用。我们很容易认识到一批材料加工制作的费用与生产加工的时间是密切相关的，随着加工时间的增加相应的费用也在不断的增加，即工人的工资及可预测提前完工的机会成本。

1.2.2 构造模型框图

仿真开始，此同处于初始状态，所有班组和桁架都空闲。根据材料相继到达的时间服从泊松分布产生随机数，仿真每批材料到达的时刻，累计到达的批数，再用离散型随机变量的仿真，确定每批到达的原材料数量。按照桁架的起吊吨位将车间划分为4个区域。当一批材料到达，将其划分到相应的区域，再确定各个班组忙碌和空闲的时间，并计算其相应的费用。重复仿真过程，得出不同工期和不同班组数的利润、劳动利用率和合理工期。

构造模型框图如图2所示。

图2 构造模型框图

标识符说明:

A:仿真次数K班组数目

C(J):第J批材料所选择起吊行架D(I):第I个班组释放时刻

T1:每批顾客到达时刻N:仿真设定时间

X1:每个班组最短释放时间F:班组空闲时间累计

E:构件到达等待时间累计SS1:C(J)=1:时班组空闲时累计费用

SS2:C(J)=1:时材料存储费用SS3:C(J)=1:时工人忙中出错的损失费用

SM1～SM12:各个费用累计值GX:各班组时间利用率

1.3 算法描述

当原材料是平均到达时，λ平均到达率为，μ为平均服务率 （即设定时间内平均能生产的数量）按照排队等待系统来分析:

平均排队等待的顾客数:

一批原材料在系统中平均排队等待时间:

一批原材料在系统中平均逗留时间:

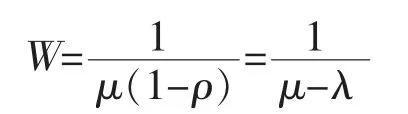
在整个系统中我们计算材料到厂后的等待时间F=F+X1-T1，班组空闲时间E=E+T1-X1，空闲时间的费用SM1=SM1+SS1,计算累计等待时间的存储费用SM2=SM2+SS2，计算因出错产生的损失费用SM3=SM3+SS3，并通过多次循环仿真得到仿真月份值A和计算班组工作时间利用率及累计年总费用SM=SM1+…+SM12，年收入TS,年利率TP=TS-SM。仿真最终得到的仿真月份即在费用最小情况下的加工时间。最终在总体成本最低的中得到体现。

2 仿真结果分析及现实意义

由仿真的过程中我们发现生产的服务台，即工人的数量由空闲时间的长短而定的，如果空闲的时间较长我们将考虑在不影响产品质量的基础上减少工人的人数，如果工人总是处于忙碌状态，而引起忙中出错的概率增加，而导致成本的上升，通过机会成本的对比，可以考虑增加工人人数。工期和费用也可以类似的进行分析。在不增加费用的基础上，可以获得最优工期与合理的员工配置。这也一直是人们所关注的问题，即在产品质量，工期，成本之间寻求的一种平衡。

在多工序生产制造业中应用仿真技术的具有其现实意义。工序虚拟仿真技术可以直观、科学地展示不同人员配置和加工过程组织协调措施的效果，可以定量地完成方案的对比，真正实现加工过程的优化；该技术还可以模拟新技术、新材料、新工艺应用后的效果；有助于生产过程管理。并能够提前发现生产过程中质量问题的产生。管理人员可以采取有效的预防、加强措施，提高构件加工生产制作过程中的管理效果，这样有助于操作人员全面了解作业过程，高效的保质保量的完成生产任务。

[1]赵能.虚拟仿真技术在建筑设计中的应用研究[D].长沙理工大学,2009.

[2]宋连成,陈红林.热轧日生产计划优化模型和算法仿真[J].计算机仿真,2008,25(7):166～169.

[3]谢行皓.建筑工程系统仿真[M].科学出版社出版,2003.