中低设防烈度地区全无缝桥梁抗震性能分析＊

马永春，邵旭东，余加勇

（湖南大学 土木工程学院，湖南 长沙 410082）

中低设防烈度地区全无缝桥梁抗震性能分析＊

马永春，邵旭东†，余加勇

（湖南大学 土木工程学院，湖南 长沙 410082）

为了准确地模拟接线路面特性，对其荷载-变形和损伤进行了分析，提出了接线路面板集中弹簧简化模型.基于此，采用SAP2000建立了某座全无缝桥梁动力计算模型.对该桥进行了模态分析和地震时程分析，并与对应连续梁桥进行了对比分析；同时还进行了桥长和接线路面刚度敏感性分析.研究结果表明：中低设防烈度地区，全无缝桥梁的地震响应只有连续梁桥的24%～35%，主桥处于弹性无损状态.可见，全无缝桥梁能大幅提升中低烈度地区公路中小桥梁的抗震性能.

地震响应；半整体式全无缝桥梁；接线路面；地震设防烈度；时程分析

据交通部权威数据统计，截至2011年年底，全国公路桥梁达689 400座，其中中小桥梁631 830座，占总桥的91.6%［1］.中小梁桥伸缩装置问题带来的桥头跳车、长期维修、定期更换问题，一直是国内外公路桥梁的通病.另外，简支梁桥在地震荷载下易出现落梁损毁，连续梁桥易出现伸缩缝和桥台受损.

伸缩缝装置问题一般有两种解决思路：一是改良伸缩缝装置；二是减少或干脆取消伸缩缝装置.基于思路一，效果不佳；基于思路二，国外一般采用整体式或半整体式无缝桥梁的方式取消桥面伸缩装置，但路－桥交界处依然存在伸缩缝［2－3］.为了克服国外无缝桥梁的缺陷，湖南大学桥梁工程研究所提出了半整体式全无缝桥梁结构体系，完全取消了伸缩缝装置［4－5］.对于常规无缝桥梁，国外大量的研究表明其抗震性能优于一般的简支梁桥和连续梁桥［6－8］.对于全无缝桥梁，其主梁、搭板、接线路面及公路串联为整体，应更具整体变形和抵抗地震能力，特别是抑制落梁、桥台冲剪等问题.然而迄今为止，针对全无缝桥梁的抗震性能还未有过专门的研究.

为了掌握这一新型半整体式桥梁的振动和地震响应特点，本文以一座已建半整体式全无缝桥为工程背景，提出接线路面板拉伸荷载－变形简化力学模型，建立全无缝桥梁弹性动力有限元模型；对全无缝桥梁及相应连续梁桥进行了自振特性和地震响应的对比分析，同时还进行了抗震性能参数敏感性分析，并对应用于中低设防烈度地区（6，7度）的全无缝桥梁的抗震性能进行了评估.

1 局部计算模型

1.1 接线路面模型

全无缝桥梁是通过连续主梁、搭板、接线路面和公路四者连串成整体来实现路－桥全无缝的.温降时主梁和搭板带动接线路面受拉，依靠接线路面板的带裂缝工作来吸纳桥梁变形［5］，可见接线路面的力学特性是全无缝桥的关键所在.温降实验表明：带裂缝接线路面板在钢筋屈服前就已表现出明显的非线性特性［9］.2012年马永春对接线路面板的拉伸力学特性进行了理论和实验研究，得到了接线路面板的弹塑性荷载－变形骨架曲线模型，如图1所示［10］.

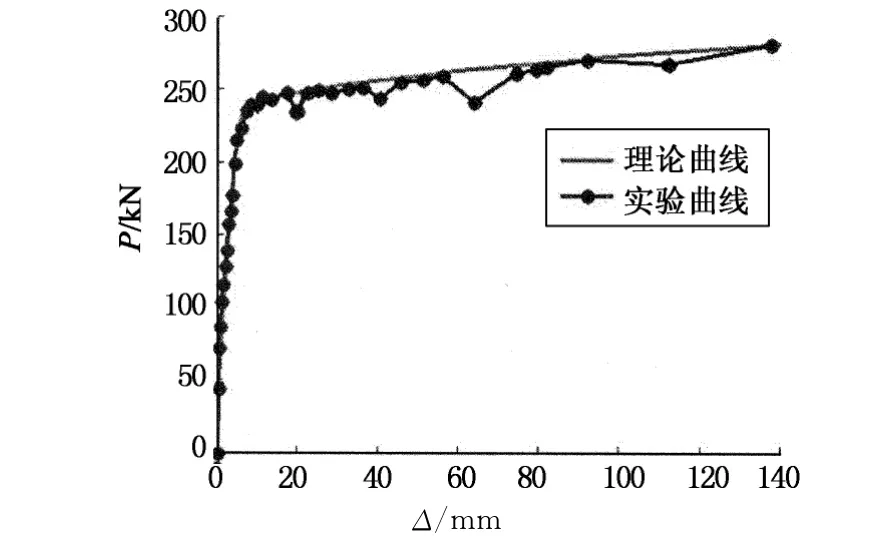
图1 接线路面板理论与试验拉伸P-Δ曲线Fig.1 Theoretical and tested P-Δcurve of CRCAP

接线路面板拉伸特性存在明显的3个性能点及3个区间，如图2所示：

图2 接线路面板拉伸P-Δ曲线简化模型Fig.2 Simplified model of P-Δcurve of CRCAP

1）点A（ΔL，PL）为拉伸荷载恰好传递到接线路面板末端但未传递到地锚时的点.在O～A范围内为区间I，接线路面板的多裂缝细小、地锚不会被拉动，路桥沥青混凝土面层处于完好无损状态.此区间便是全无缝桥梁正常使用性能区间.

2）点B（Δy，Py）为接线路面板裂缝面处钢筋首次达到屈服荷载时的点.在A～B范围内为区间II，接线路面板卸载后裂缝都能自行闭合，其路面层基本无损，但地锚与路交界处的路面可能被拉裂（地锚刚度不够时）.

3）点C（Δu，Pu）为接线路面板拉断时的点.在B～C范围内为区间III，接线路面板会出现较大的裂缝，引起路面层出现反射裂缝，同时地锚与路的交界处会出现较宽的裂缝，但实验表明接线路面板延性非常好，不会出现拉断的现象.

显然，在区间I中，整个接线路面无损，满足正常使用要求（小震不坏）；在区间II中，接线路面板依然处于弹性状态，仅地锚和路的交界处路面出现较大的开裂损伤，但通过灌缝很容易修复（中震可修）；在区间III中接线路面板、地锚和路交界处都会出现较大的裂缝，不再满足正常使用要求，但不会出现拉断损坏（大震不倒）.可见，把上述A，B，C3点作为接线路面板抗震损伤分析的性能点是合理的.

为了计算的方便，基于上述3个性能点，对曲线进行简化，简化模型如图2所示.

初始线性段—OA，初始有效刚度为：

第三线性段—B′C，几近直线，简化模型采用其切线，刚度为：

第2，3直线的交点B′即为等效拉伸屈服强度Peq.

另外，全无缝桥梁为达到路桥全无缝的目标，接线路面的设计、施工遵循了3条原则：1）温降时，通过合理的配筋、板长等设计，达到多裂缝吸纳主梁变形和尽量不拉动两端地锚的目的；2）温升时，采取在温度上限的条件下合龙主桥和接线路面，以实现常态下接线路面处于拉伸多裂缝开裂状态，达到地锚受到较小推挤作用的目的；3）选用合理刚度的地锚.

综上所述，接线路面纵桥向初始刚度仅由接线路面板初始刚度贡献，对全无缝桥梁进行模态分析时，应取初始有效刚度K1；对中低设防烈度地区进行时程分析时，如果接线路面变形响应较小、没有扰动地锚时，也应采用K1进行计算.

1.2 支座模型

全无缝桥梁的支座一般都设置为板式橡胶支座.板式橡胶支座可用线性弹簧单元模拟，竖向和水平向刚度按式（4）计算［11］：

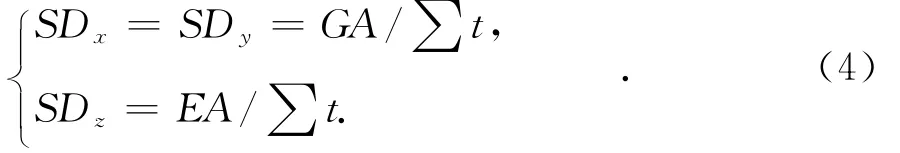
式中：SDx，SDy和SDz分别为横桥向、顺桥向和竖向刚度；A为支座的承压面积，mm2；G为支座的动剪模量，MPa，一般取G＝1.2MPa；∑t为橡胶片的总厚度，mm；E为支座的抗压弹性模量，MPa，E按式（5）计算［12］：

式中：S为支座形状系数，圆形支座S＝d0／4t1；t1为支座中间单层橡胶片厚度，mm；d0为圆形支座加劲钢板直径，mm.

1.3 桩土相互作用模型

建立桥梁抗震分析模型应考虑桩土的相互作用，桩土相互作用可用等代土弹簧模拟，土弹簧的刚度Ks采用表征土介质弹性值的m参数来计算［11］：

其中：z为弹簧位置处土层的深度；a，b分别为土层厚度和该层的宽度，b常取桩的计算宽度，圆形单桩取b＝0.9（d＋1），d为桩径［13］；另外，在动力分析中一般地取m动＝（2～3）m静，m静应通过实验确定，缺乏实验资料时，可根据地基土分类，状态按《公路桥涵地基与基础设计规范》［13］表P.0.2－1查用.

2 模态分析

2.1 工程概况

本文以某座已建全无缝桥梁为基准分析模型.上部结构主梁为3×20m预应力标准空心板，先简支后桥面连续，桥梁全长66.08m，单幅桥宽16.25 m；搭板长5m、厚30cm；接线路面板长30m、厚24 cm，C30混凝土、纵向配筋率0.8%；沥青混凝土路面厚10cm.每片空心板下布设板式橡胶支座.下部结构为半整体式桥台，桩柱式桥墩，钻孔桩基础；桥墩直径为1.4m，高5.0m；桩基直径1.5m，长36 m.全桥立面布置及竣工后实桥如图3（a）和图3（b）所示.

根据设计参数、文献［10］编辑的MATLAB非线性程序及本文公式（1）～（3），便可求得延米宽接线路面板力学性能和简化模型的参数值，如表1所示.

表1 接线路面板力学特性值Tab.1 The mechanical properties of the approach pavement slab

2.2 全桥计算模型

采用有限元程序SAP2000建立全桥结构动力分析模型，如图3（c）所示.主梁、桥墩和桩基均采用空间弹性梁单元进行模拟；搭板采用弹性厚板单元模拟，路基对其支撑采用大刚度的只受压平面弹性支承单元模拟 （全无缝桥梁设计时，为了减小搭板底的摩擦力，在搭板和路基间铺设了两层土工布，故本文不考虑水平摩擦效应）；接线路面采用水平向的等效节点弹性单元进行模拟，其刚度取值采用上述的初始有效刚度K1，同时接线路面的质量以节点质量的形式集中到搭板末端；板式橡胶支座采用三向刚度弹性连接单元模拟；桩土相互作用采用节点弹性单元模拟；桩基底部固结.采用集中质量法考虑质量矩阵.时程分析时，模型采用瑞利阻尼.为了比较连续梁桥改进为全无缝梁桥后动力性能的变化，本文还建立了该桥对应的连续梁桥模型.

图3 一座全无缝桥梁结构及分析模型Fig.3 A fully jointless semi-integral bridge

2.3 分析结果

基于上述有限元计算模型，采用子空间迭代法，计算了该全无缝桥和其对应连续梁桥前50阶振型.取前10阶频率和振型特征示于表2.由结果可知：全无缝桥梁和连续梁桥的振型和频率非常类似.振型方面：第一振型都是纵桥向漂移，而且其它各阶振型及出现顺序基本一致.频率方面：除了第一阶固有频率相差很大外（全无缝桥型／连续梁桥型＝2.2倍），其它各阶频率基本一致.可见，全无缝桥梁的接线路面对主梁纵向振动影响很大，对竖向振动基本无影响.

全无缝桥梁和连续梁桥第一阶振型参与质量都很高：分别为91.42%和88.95%.可见全无缝桥梁纵桥向振动也是以第一阶纵漂振动为主.

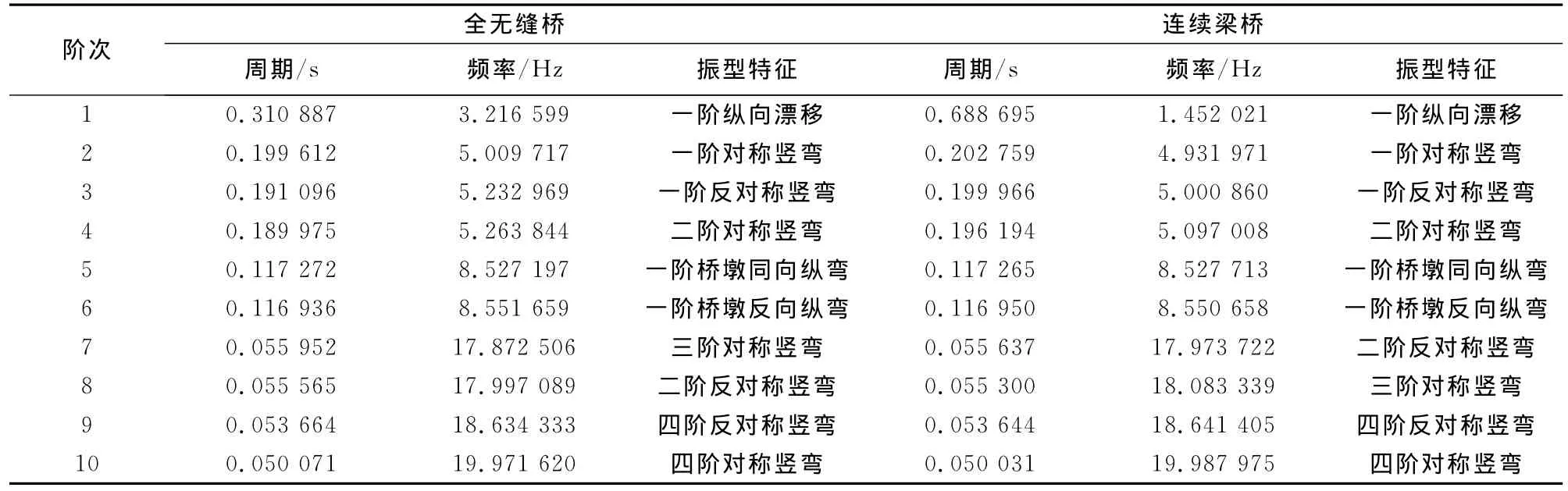
表2 全无缝桥和连续梁桥前10阶自振特性Tab.2 The vibration characteristics of a FJSB and continuous girder bridges

3 地震响应分析

3.1 地震荷载

本文旨在对中低抗震设防烈度地区（≤7度）的半整体式全无缝桥梁进行抗震性能分析.全无缝桥梁主要应用在高速公路、一级公路或二级公路中，其抗震设防类别属于B，C类.B，C类桥梁的抗震设防性能目标为：小震（重现期约为50～100年）不坏，中震（重现期约为475年）可修，大震（重现期约为2 000年）不倒.各等级地震动是通过基本设防烈度地震动峰值加速度A乘以重要性系数来实现的.B类桥梁小震、中震和大震对应的重要性系数分别为0.43，1.0和1.3.基本地震动加速度峰值取设防烈度7度地区对应的最大值0.15 g.综上所得各级地震动峰值分别为［11］：

采用3组地震波进行时程分析，最终结果取3组计算结果的最大值.本文主要针对地质条件比较好的II场地进行时程分析，天然地震波选用塔夫特地震波（适用于中硬场地），另外2条为人工地震波，采用SIMQKE软件拟合反应谱得到.地震动峰值按上述小震、中震和大震三级进行调整.

3.2 地震时程分析

为了比较全无缝桥梁与连续梁桥地震响应的差别，对这两种桥型分别进行了小震、中震和大震三水平的时程分析.分析结果如表3所示，表中“A”代表连续梁桥，“B”代表全无缝桥.从中可以得到以下结论.

由于受到接线路面的限制，全无缝桥梁主梁纵飘位移（即桥台支座变形）、墩顶支座变形分别仅为对应连续梁桥的24%和20%，且都远小于支座变形设计值；而大震作用下，连续梁桥支座最大变形高达30.7mm＞支座变形设计值30mm.可见，接线路面大大减小了全无缝桥梁的位移和变形响应，这对抗落梁、抗桥台冲剪和保护支座都非常有利.

表3 全无缝桥梁和连续梁桥地震响应对比Tab.3 The comparison of seismic response between FJSBs and continuous girder bridges

全无缝桥梁桥接线路面变形为：Δ小震＝2.4mm和Δ中震＝5.6mm，基本都在0～5.4mm（假设常态时，接线路面变形处于温度上下限的中间，ΔL／2＝10.8mm／2＝5.4mm，处于区间Ⅰ；Δ大震＝7.3mm落在5.4mm～19.5mm（Δy－ΔL／2＝24.9mm－5.4＝19.5mm），处于区间Ⅱ.可见，全无缝桥梁在小震和中震作用下路和桥沥青混凝土面层都处于完好无损的状态；在大震作用下，地锚与路交界处的路面可能出现较小裂缝.

全无缝桥梁桥墩的最大弯矩及对应剪力响应都为连续梁桥的35%，且都远小于弹性抗力极限值；而连续梁桥在大震作用下，桥墩最大弯矩达到2 709 kN·m＞桥墩的初始屈服弯矩2 633kN·m.可见，全无缝桥梁能有效地降低纵桥向桥墩的损坏，即使在7度地区大震作用下桥墩依然处于弹性状态，而连续梁桥的桥墩则会出现较为严重的开裂.由于全无缝桥梁的搭板与主梁结构连续，在地震和温度等荷载作用下都会引起边跨主梁一定的附加弯矩.本文地震引起的全无缝桥梁边跨跨中弯矩为59～180 kN·m，虽是连续梁桥的4.5倍，但只有对应自重引起弯矩（943kN·m）的6%～19%（也远小于活载的响应）.可见，中低设防烈度地区，接线路面引起的边跨主梁的附加弯矩对主梁影响很小，不会造成损伤.

4 参数敏感性分析

4.1 主梁长度

全无缝桥梁一般都是在标准跨径（如20m标准预应力空心板）简支梁桥的基础上，通过主桥先简支后桥面连续及接线结构无缝化的方法来实现路桥全无缝.现已建成的全无缝桥梁桥长主要为2×20 m，3×20m，4×20m和5×20m.为了全面掌握各种桥长的全无缝桥梁在中低设防烈度地区的地震响应情况，分别对上述4种桥长的全无缝桥梁进行了时程分析.计算模型以2.2中全桥计算模型为基准，仅仅把主桥改设为2×20m，3×20m，4×20m和5×20m4种情况.接线路面刚度、地震荷载等保持不变.计算结果如表4所示，小震、中震和大震分别用X，Z，D表示.从分析结果可以看出：

随着主梁长度的增加，全无缝桥梁的位移变形响应和内力响应都呈增加趋势，且位移变形响应的增幅要大于内力响应的增幅.然而，地震响应最大的5×20m全无缝桥梁的桥墩、主梁、支座都处在弹性抗力范围内，主梁最大位移也仅有11.0mm，不会冲撞桥台.

随着主梁长度的增加，接线路面的变形也越来越大.除了各级地震作用下的2×20m全无缝桥和小震作用下的4种典型桥长全无缝桥的接线路面变形 （即主梁位移）落在性能区间1，沥青混凝土路面都是平顺无损的；其它情况都落在性能区间2，接线路面板路面层会出现细裂缝，但震后会弹性闭合，同时地锚与路交界处的路面可能出现开裂现象.

随着桥长和地震作用的增大，接线路面的变形量逐渐进入性能区间Ⅱ，即对地锚的扰动越来越大.这预示着，在桥长较长、地震烈度较大的地区，接线路面中设置地锚显得越发重要.

表4 桥长对全无缝桥梁地震响应的影响Tab.4 The seismic response of FJSBs under different bridge length

4.2 接线路面刚度

从前面的模态分析和地震响应分析可以看出，接线路面的刚度对全无缝桥梁的振动影响很大.本部分仅将2.2中全桥计算模型的接线路面刚度（单位：kN／m）设置成如表5所示的9种等级进行时程分析，地震荷载同前.从表5的计算结果，可以看出：

随着接线路面刚度的增加，主梁纵桥向位移、支座变形、墩底最大弯矩及对应剪力都显著递减.可见，增大接线路面刚度能有效地减小全无缝桥梁全桥的位移响应和桥墩的内力响应，是控制落梁、支座破坏、桥台冲剪和桥墩损伤的最有效措施.

当接线路面每延米宽的刚度增大到100 000 kN／m时桥墩的内力响应出现最小值，再增大刚度响应反而会小幅升高.可见，即使不考虑经济效益，通过一味地增大接线路面刚度来增强全无缝桥梁抗震性能也是不合理的.

随着接线路面刚度的增加，边跨主梁弯矩响应呈先增大后减小的趋势.峰值弯矩为360kN·m，仅为边跨自重弯矩（943kN·m）的38%，也远小于活载弯矩.可见，中低设防烈度地区，接线路面引起的边跨主梁弯矩不会造成主梁损伤.

无论在何种接线路面刚度情况下，随着地震作用的增大，各项地震响应都会增大.因此，选择合理接线路面刚度时，还应考虑桥址地震大小情况.

由于接线路面刚度＝接线路面板刚度＋地锚刚度，且常规设计完成后，接线路面板的刚度随之确定，所以唯有通过增强地锚刚度的方式来增大接线路面刚度，最终达到增强全无缝桥梁的抗震性能.

表5 接线路面刚度对全无缝桥梁地震响应的影响Tab.5 The seismic response of FJSBs under different approach pavement stiffnesses

5 结 论

根据接线路面不同的受力和损伤状态，把接线路面板拉伸荷载－变形曲线划分为3个区间，并据此提出了接线路面板拉伸曲线的3线性简化模型.这为建立全无缝桥梁动力模型，进行模态分析和地震时程分析打下了基础.

全无缝桥梁和连续梁桥的振型和频率非常类似.振型方面：第一振型都是纵桥向漂移，而且其它各阶振型及出现顺序基本一致.频率方面：除了第一阶固有频率相差很大外，其它各阶频率基本一致.另外，全无缝桥梁第一阶振型参与质量高达91%，纵桥向振动以第一阶纵漂振动为主.

全无缝桥梁的主梁由于受到接线路面的限制，全无缝桥梁主梁纵飘位移和墩顶支座变形分别仅为对应连续梁桥的24%和20%；墩底最大弯矩和剪力响应也只有对应连续梁桥的35%；唯有边跨主梁弯矩响应是连续梁桥的4.5倍，但最大弯矩值也仅为自重响应的19%（不足以造成主梁损伤）.可见，全无缝桥梁不存在伸缩装置破损，对抗落梁、抗桥台冲剪、保护支座和桥墩都非常有利，抗震性能明显地优于简支梁桥和连续梁桥，是一款抗震性能非常优秀的中小型桥梁.

中低烈度地区4种典型桥长的全无缝桥梁抗震分析表明：随着桥长的增加，全无缝桥梁的位移响应和内力响应都呈增加趋势，但桥墩、主梁、支座都处在弹性抗力范围内.另外，各级地震作用下的2×20 m全无缝桥和小震作用下的4款全无缝桥的接线路面处于性能“区间I”：完好无损；其它情况的接线路面处于性能“区间II”：出现细裂缝，但震后会弹性闭合、地锚与路交界处会出现较小的开裂现象.

接线路面刚度参数敏感性分析表明：随着接线路面刚度的增加，主梁纵桥向位移、支座变形、墩底弯矩及剪力都显著递减；主梁弯矩响应存在一个极大值，但值较小.可见，接线路面刚度是控制全无缝桥梁抗震性能的最敏感参数.在经济合理的前提下，采用刚度较大的地锚对全无缝桥梁抗震是有利的.

［1］ 中华人民共和国交通运输部.2011年公路水路交通行业发展统计 公 报 ［EB／OL］／／［2012-04-25］http：／／www.moc.gov.cn／

zhuzhan／tongjigongbao／fenxigongbao／hangyegongbao／201204／t20120425＿1231778.html.Department of Transportation of the People＇s Republic of China.Road and water transportation industry development statistical bulletin of 2011 ［EB／OL］／／［2012-04-25］http：／／www.moc.gov.cn／zhuzhan／tongjigongbao／ fenxigongbao／hangyegongbao／201204／t20120425＿1231778.html.（In Chinese）

［2］ AROCKIASAMY M，BUTRIENG N，SIVAKUMAR M.State-of-the-art of integral abutment bridges：design and practice［J］.Journal of Bridge Engineering，2004，9（5）：497－506.

［3］ RODOLFO F M，SAMER H P.Integral abutments and joint-less bridges（IAJB）2004survey summary［C］／／FHWA Conference.Baltimore，USA：FHWA，2005：12－26.

［4］ JIN Xiao-qin，SHAO Xu-dong.Experience of innovative integral bridges in China［C］／／Proceedings of 7th International Conference on Short ＆ Medium Span Bridgesin，Canada.Washington，DC：TRB，2006.

［5］ 金晓勤，邵旭东.半整体式全无缝桥梁研究［J］.土木工程学报，2009，42（9）：68－73.

JIN Xiao-qin，SHAO Xu-dong.A study of fully jointless bridge-approach system with semi-integral abutment［J］.China Civil Engineering Journal，2009，42（9）：68－73.（In Chinese）

［6］ MARTIN P，BURKE J.Integral bridges［J］.Transportation Research Record，1990，1275：53－61.

［7］ SOLTANI A A，KUKRETI A R.Performance evaluation of integral abutment bridges［J］.Transportation Research Record，1992，1371：17－25.

［8］ WASSERMAN E P，WALKER J H.Integral abutments for steel bridges［M］.Tennessee：American Iron and Steel Institute，1996.

［9］ 邵旭东，占雪芳.带地梁的新型半整体式无缝桥梁温度效应研究［J］.中国公路学报，2010，23（1）：43－48.

SHAO Xu-dong，ZHAN Xue-fang.Temperature effect of innovative semi-integral abutment jointless bridge with ground beam［J］.China Journal of Highway and Transport，2010，23（1）：43－48.（In Chinese）

［10］马永春，邵旭东，梁才.全无缝桥梁接线路面拉伸力学特性理论和实验研究［J］.地震工程与工程振动，2012，32（4）：30－37.

MA Yong-chun，SHAO Xu-dong，LIANG Cai.Theoretical and experimental study on tension-deformation mechanical properties of continuously reinforced concrete approach pavement of FJSBs［J］.Journal of Earthquake Engineering and Engineering Vibration，2012，32（4）：30－37.（In Chinese）

［11］JTG／TB02-01－2008 公路桥梁抗震设计细则［S］.北京：人民交通出版社，2008.

JTG／TB02-01－2008 Guidelines for seismic design of highway bridges［S］.Beijing：The China Communications Press，2008.（In Chinese）

［12］JT／T 4－2004 公路桥梁板式橡胶支座［S］.北京：人民交通出版社，2004.

JT／T 4－2004 Plate Type elastomeric pad bearings for highway bridges［S］.Beijing：The China Communications Press，2004.（In Chinese）

［13］JTG D63－2007 公路桥涵地基与基础设计规范［S］.北京：人民交通出版社，2007.

JTG D63－2007 Code for design of ground base and foundation of highway bridges and culverts［S］.Beijing：China Communication Press，2007.（In Chinese）

Seismic Analysis of the Fully Jointless Bridge in the Low Seismic Fortification Intensity Zone

MA Yong-chun，SHAO Xu-dong†，YU Jia-yong
（College of Civil Engineering，Hunan Univ，Changsha，Hunan 410082，China）

To accurately simulate the characteristics of continuously reinforced concrete approach pavement（CRCAP），a simplified concentrated spring model was proposed according to the force-deformation curve and the damage level of the CRCAP.Based on this，a dynamic finite element model of a semi-integral fully jointless bridge（SFJB）was established with SAP2000.The Modal analysis and Time History analysis were carried out on both the SFJB and the continuous girder bridge（CGB）for comparison.The sensitivity analysis of seismic performance was also investigated.The results indicate that the seismic response of the SFJB is only 24%～35%of the CGB in the low seismic fortification intensity zone，which can greatly enhance the seismic resistance of small and medium bridges.

seismic response；semi-integral fully jointless bridge；approach pavement；seismic fortification intensity；time history analysis identification algorithm

U442.55

A

1674-2974（2013）05-0011-07

2012-07-17

国家自然科学基金资助项目（50908083）；国家西部交通建设科技项目（2009318000044）

马永春（1981－），男，湖南常德人，湖南大学博士研究生

†通讯联系人，E-mail：shaoxd＠163.vip.com