基于热网络法的隔离开关热稳定性分析

王稚惠，谢 勇，由佳欣，梁慧敏，翟国富

(1.哈尔滨电机厂有限责任公司黑龙江哈尔滨 150040; 2.桂林航天电子有限公司，广西桂林 541002;3.哈尔滨工业大学黑龙江哈尔滨 150001)

基于热网络法的隔离开关热稳定性分析

王稚惠1，谢 勇2，由佳欣3，梁慧敏3，翟国富3

(1.哈尔滨电机厂有限责任公司黑龙江哈尔滨 150040; 2.桂林航天电子有限公司，广西桂林 541002;3.哈尔滨工业大学黑龙江哈尔滨 150001)

隔离开关在实际运行中由于电阻损耗发热而温度升高，甚至超过允许温升，从而影响其工作性能。为了保证其工作的安全性和可靠性，建立了热网络模型，对隔离开关进行端部温度及最高温度的计算与分析，并对比有限元三维仿真结果验证了热网络方法的准确性。该方法可用于工程现场应用，便于快速得到精确的计算结果。

隔离开关;热稳定性;热网络法

1 引言

在长期运行中，隔离开关自身温度上升到一定极限值时，就会加速绝缘的老化，甚至破坏绝缘，直接影响其使用寿命和相关设备的安全。因此，研究和预测隔离开关的发热，具有重要意义［1］。

通常，元器件中接触电阻产生的焦耳热会使收缩区的温度升高，严重时会使两接触面产生熔焊，这是隔离开关无法消除的危害热源。由“斑点”接触的微观特征引发的收缩电阻及接触热阻，一直以来都是国内外学者关注的热点，并对电接触的稳态热效应、暂态热效应及电接触的热过程数学模型等问题等进行了大量的相关研究［2－8］。文献 ［9］中应用有限元软件Ansys针对断路器中大电流负载的典型触头结构，分别进行了机－电－热的耦合场稳态、瞬态仿真分析。仿真结果与试验结果具有很好的一致性，但对设计和工程技术人员来说，解析计算模型相比有限元模型具有计算快速，参数关系直观显现等特点，对于定性分析、工程现场应用的器件初始设计均具有重要的价值。热网络法是基于热路与电路相似性原理，提出的一种热分析方法。用热阻和热源代替实际开关元件来建立热网络模型，采用求解电路的相关理论对热路进行求解。

本文以高压隔离开关为研究对象，基于热网络法，对其进行热件划分、热网络合成以及解析表达。首先以导电接触系统热平衡过程为理论基础，并根据隔离开关的具体形状以及热流方向，将其进行热件的合理划分;然后基于热路和电路的对偶相似性，将各个热件等效为四端口，使其具有同样的外特性;再根据隔离开关具体热流方向以及各热件之间的关系，将热件进行合成，建立热网络模型，并通过对网络模型的分解，求得各四端口即热件的端部变量;在此基础上，最终求得隔离开关的温度分布以及最高温升。最后，将计算结果和有限元仿真数据进行对比，验证方法的准确性。

2 热件的基本类型及隔离开关热件的划分

采用热网络法进行隔离开关的稳态温升分析，需要将隔离开关的实体结构等效成能够用热路相关理论分析的热网络。由于热网络是由很多个基本的四端口网络所组成，因此整个热分析过程的第一步即为将隔离开关各部分划分热件。

2.1 热件的基本类型

热件，即发热元件，是热网络模型中最小的单元。综合发热及散热情况的不同，可以将热件分成四类，即无源集中参数热件、无源分布参数热件、有源集中参数热件和有源分布参数热件［10］。

根据热路和电路相似性的基本原理，每个热件都可等效为一个含热阻或热源的四端口网络，端口的一般表达式为:

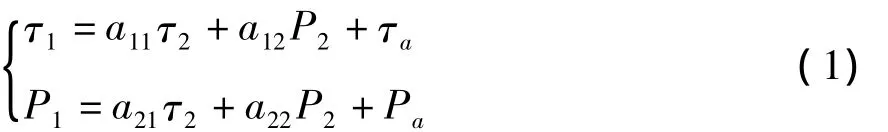
其矩阵表示为:

式中，τi——温升(℃);pi——热流(W);

τa，pa——热件中与热源相关的量，类似于电路中的电压源与电流源。

2.2 隔离开关热件的划分

本文以某型号隔离开关为研究对象 (如图1)，由于其结构的对称性，首先对1/2隔离开关进行热件的划分，再将其对称到另1/2的模型，即可完成隔离开关热件划分的过程。

图1 接触系统结构图

图2所示为1/2隔离开关热件示意图。其中，热件1、8为有源集中参数热件，热件13为无源分布参数热件，其它热件均为有源分布参数热件。

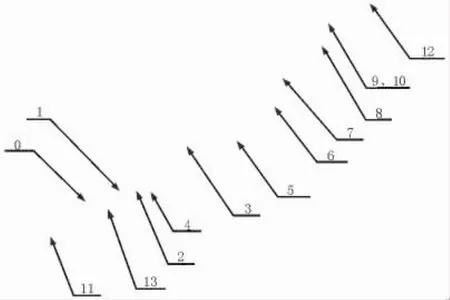
图2 1/2隔离开关热件示意图

上述四种热件类型的划分，在理论上是比较合理的，但只适用于有源匀质单向热导体的模型。不同的热件，由于形状、发热及热传导情况的不同其具体的矩阵参数计算过程也有所不同。为了较为简洁地阐述热件的计算过程，按参数计算的特点，将热件分为单向导热件、非单向导热件和触头接触部分。单向导热件为传热方向单一的热件，非单向导热件为传热方向不唯一的热件。触头接触部分比较特殊，需单独研究。在图2中，热件2、3、4、5、6、7、9、10、13为单向导热件，热件0、8、11、12为非单向导热件，热件1为触头接触部分。

3 隔离开关热件参数的计算及热网络模型的建立

3.1 隔离开关热件参数的计算

对于单向导热件，如图3所示。

图3 单向导热件

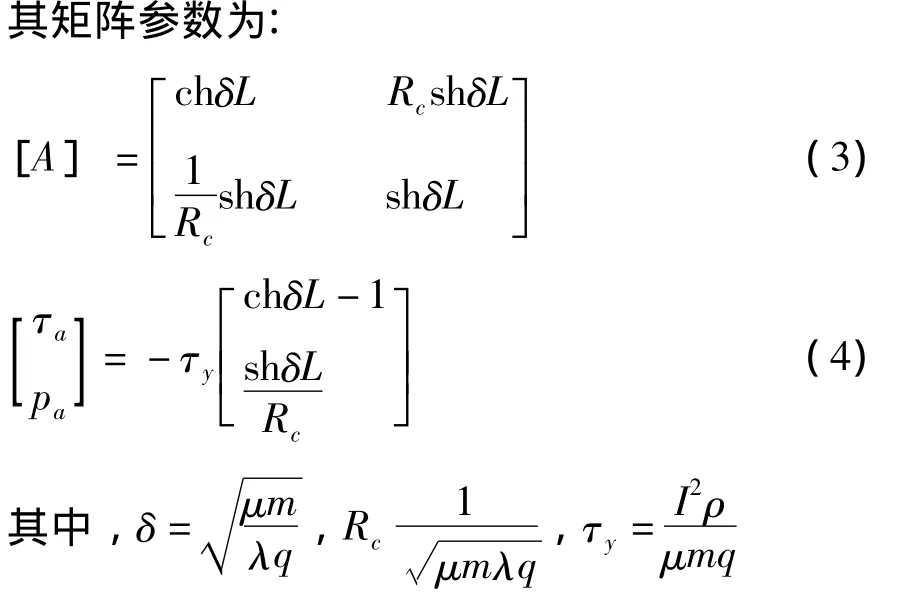
式中，μ——表面散热系数 ［W/(℃ · m2)］;

m——热件的周长(m);

λ——热导率［W/(℃·m)］;

q——热件的截面积(m2);

I——流过热件的电流(A);

ρ——热件的电阻率(?/m)。

对于非单向导热件，其四端口网络如图4所示。

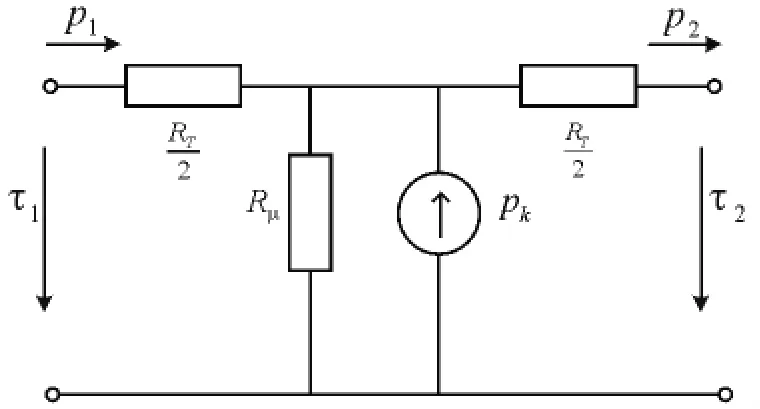
图4 非单向导热件的四端口网络

其中，RT为传导热阻，Rμ为表面散热热阻，pk为热件的发热功率。其矩阵参数为:

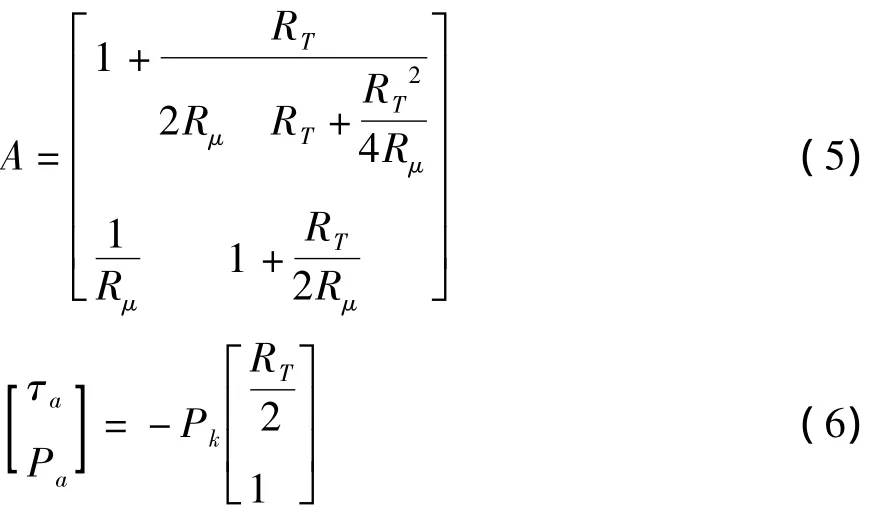
对于触头，其四端口网络如图5所示

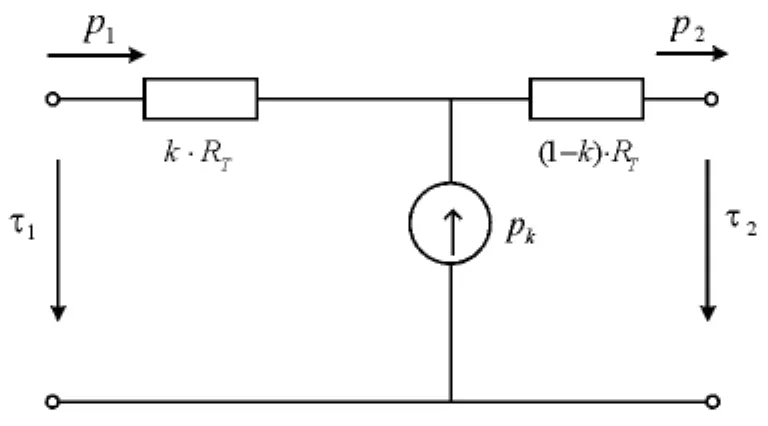
图5 触头的四端口等效热路

k是由于触头的接触处结构不对称而引入的，一般取k=0.3 0.5。

3.2 隔离开关热网络模型的建立

上述无源热件及有源热件等效网络为单个热件的等效网络，在实际热路中，沿热流的传导方向上有多个热件分布，每个热件都需等效为一个四端口网络。将热件合成网络，即可建立整体的热网络模型。四端口网络联接的方式有多种，即并联、链联以及混联。

按图2所示的隔离开关热件的划分，根据各个热件之间的传热关系，可合成隔离开关的热件网络，如图6所示，其中Rc为一对隔离开关的传热部分，作为边界热阻计算。根据上述热网络合成的过程，能够求出隔离开关热件合成网络及相关参数。

在对隔离开关热件的网络进行局部合成时，仅有链联和并联网络合成两种情形，将热件0～13进行网络参数的合成。根据本文研究的隔离开关的属性参数，最终得到总网络模型的参数为:

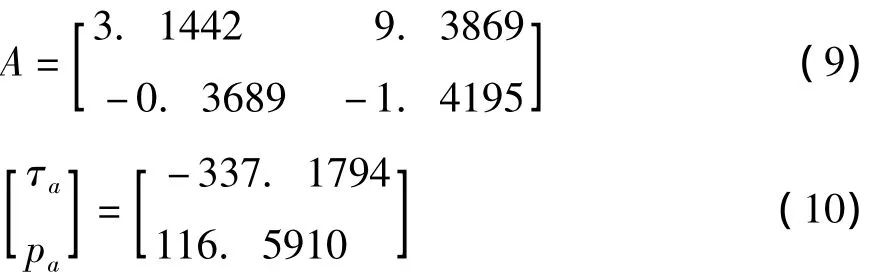
3.3 隔离开关的边界条件

在求得的总网络模型参数的基础上，还需确定边界条件，才能对隔离开关端部温升进行计算。

根据开关电器热路的实际情况，可将热网络法的边界条件分为三种:断路条件、环路条件和恒压条件［10］。上述隔离开关符合恒压条件。此时的边界条件的方程为:

式中，τ∑0——始端温度;

τ∑e——末端温度。

根据以上求得的隔离开关热网络模型以及边界条件的等值网络，可以对隔离开关端部温升进行计算。

4 隔离开关温度分布及温升计算

网络求解主要目的是确定各个热件的端部温升。求解可分为两个步骤:先由合成网络及边界条件求得合成网络的端部温升;再逐步分解热网络求得各热件四端口网络的温升。

在求出各个热件四端口的温升以后，根据各个热件内部的温升规律可确定隔离开关的温度分布及其最高温升。以某型号隔离开关为例，研究在额定电流2.7kA下的最高温升及温度分布。

由于网络合成过程涉及矩阵运算，计算量较大，需要用计算机编程进行计算。使用的计算工具为Matlab，计算出各个热件的端部温升，得到隔离开关的温度分布结果。

图6 隔离开关热件的网络图

表1 隔离开关端部温度计算结果表 (热件0～5)

表2 隔离开关端部温度计算结果表 (热件6～10)

计算结果如表1与表2所示，其中温度的下标与热件编号一一对应，表示热件热流流入端口一侧的温度。

由表1与表2可知，隔离开关在额定电流2.7kA下的最高温升热件为热件1，即触头接触部分，温升为67.8℃，在隔离开关允许温升范围之内。因此，在通入额定电流2.7kA时，隔离开关可稳定、正常工作。

5 有限元仿真验证

为验证仿真计算的准确性，对隔离开关进行三维有限元模型仿真分析，额定电流为2.7kA。如图7所示，依据隔离开关的实体尺寸以及各部件的关系建立有限元模型，并对其分网、加载，最终得出仿真计算结果。

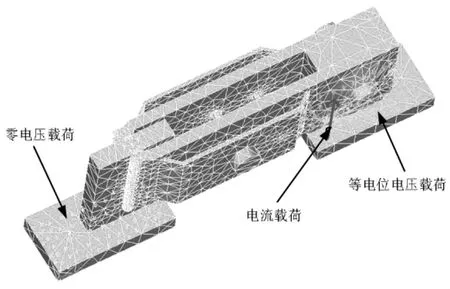
图7 隔离开关仿真载荷示意图

由表3、表4可知，解析计算结果普遍低于仿真结果，最大相对误差为12.36%，发生在静簧片底座位置即热件0，由于静簧片底座位置热流方向不定，虽然将其归为非单向导热件，但要使计算

结果与实际热流相符，还是存在一定困难。在触头接触部分及其周围热件即热件1～5，相对误差较低，平均误差为－1.80%。因此，由热网络法计算隔离开关触头周围温升能够满足一定精度要求。验证了解析计算的准确性。

表3 隔离开关端部温度计算与仿真结果对比及误差表(热件0～5)

表4 隔离开关端部温度计算与仿真结果对比及误差表(热件6～10)

6 结论

(1)根据热网络法基本原理，分析了隔离开关中热件的基本类型，并对隔离开关进行了热件划分。合成热件，建立了某型号隔离开关的完整热网络模型。本文以某高压隔离开关为研究对象，建立隔离开关的热网络模型，确定了模型的边界条件。

(2)在额定电流2.7 kA下，使用热网络模型对隔离开关各热件的端部温升进行编程计算;得到各个热件的温升。其中，最高温升的热件为热件1，即触头接触部分，其最高温升为67.8℃。

(3)热网络法计算结果与有限元仿真结果相对比，平均误差为－5.79%，验证了热网络法计算的准确性。因此，该方法可用于工程现场应用，便于快速得到精确的计算结果。

［1］ 李震彪，张逸成，程礼椿.电器热稳定性的理论分析［J］.中国电机工程学报，1998，18(1):26－28.

［2］ 张凯.基于ANSYS有限元分析的电器触头系统电动力的研究［D］.河北工业大学硕士论文，2006:12－16.

［3］ 贾真.铜铝复合母线排的电学性能及界面稳定性的研究［D］.河北工业大学硕士论文，2004:18－19.

［4］ Y.Kanno，T.Amemiya，N.Takahashi，N.Kobayashi.the Short Circuit E lectromagnetic Force of the Tree－Phase Encapsulated Gas Insulated Bus－Bar［J］.IEEE Transactions on Power Apparatus and Systems，1984，103(6):1386－1393.

［5］ Bing Shen，Xiaofeng Zhang，Dahua Zhou.Analysis and Calculation of Short－Circuit Electro－dynamic Forces on Rectangular Bus－Bars［C］.Proceedings of the 6th IPEMC，2009:2618－2621.

［6］ W.R.Wilsoin，L.L.Mankoff.Short－Circuit Forces in Isolated－Phase Busses［J］.IEEE Transactions on Power Apparatus and Systems，1954:382－396.

［7］ 翟国富，孙韬，任万滨.继电器触点分断过程瞬态热场仿真方法 ［J］.中国电机工程学报，2009，29 (9):118－123.

［8］ 丁斌，杨宁，王志萍.基于ANSYS耦合场分析的电器装置温度场仿真［J］.低压电器，2010，(2):9－12.

［9］ 郑必成.继电器瞬态温度场仿真计算及其实验［D］.华中科技大学硕士论文，2008:4－5.

［10］徐近霈.电器稳定发热计算的新方法［J］.高压电器，1982，(5):3－17.

Thermal Stability Analysis of Disconnecting Sw itch Based on Thermal Network Method

WANG Zhihui1，ZHENG Yanm ing2，YOU Jiaxin2，LIANG Huim in2，ZHAI Guofu2
(1.Harbin Electric Machinery Company Limited，Heilongjiang，Harbin，150040; 2.Harbin Institute of Technology，Heilongjiang，Harbin，150001)

The working performance of disconnecting switch is affected by the maximum permissible temperature exceeding which is caused by the heat loss of resistance.Thermal network model of disconnecting switch is established.It is used for calculation and analysis of the end point temperature and maximum temperature to ensure its safety and reliability.The accuracy of the thermal network model was verified by the results of 3D finite element method simulation.This method can be used for fast calculation under the accuracy request in engineering field.

disconnecting switch，thermal stability，thermal network method

10.3969/j.issn.1000－6133.2013.02.009

TM564.1

A

1000－6133(2013)02－0038－06

2013－01－19

试验与检测