无支撑多级支护结构稳定性与破坏机理分析
2013-03-04程雪松
郑 刚 ,程雪松 ,刁 钰
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300072;2. 滨海土木工程结构与安全教育部重点实验室,天津300072)
随着我国现代化城市建设进度的加快,大型综合多功能建筑群不断涌现,与此同时,与之相配套的基坑面积也愈来愈大,越来越深,尤其在沿海软土地区,这些大面积基坑给地下工程建设提出了很大的挑战.土质条件差、面积超大、平面形状复杂、开挖深度深且深浅不一等是这类基坑的典型特点.如何在处理这类基坑时达到安全性、经济性及环境友好性的统一,是岩土工程师们亟待解决的课题.
由于此类基坑面积大、形状复杂,采用传统的内支撑支护结构体系成本高、施工难度大,因此近些年国内进行了软土中超大面积无支撑支护技术的尝试,在天津和上海等地得到初步应用.除了最传统的悬臂排桩、重力式挡土墙、放坡等支护方法,目前常用的新型无支撑技术还包括双排桩、预留反压土等.双排桩是20世纪80年代出现的支护结构,最初应用于边坡治理,随后逐步被推广到基坑工程中[1].双排桩采用门架式的空间结构,具有较大的整体抗侧移刚度,因此在无支撑的条件下相对于单排桩有更大的支护深度.如今,双排桩有了更多的工程应用,取得了较好的经济与社会效益的同时,也积累了一定的工程经验.另外,国内也有许多学者对双排桩的变形与受力性状进行了研究,并且提出了一些具有实用价值的设计计算理论[2-5].在基坑面积较大时,预留反压土是一个经济有效的支护方法[6],虽然有一些学者对反压土的支护机理及设计方法进行了研究[6-9],但总体来讲,这种方法目前应用还不够广泛,还需要更多的实践和研究来推动其发展.
在天津地区,当基坑深度适中时,可以考虑采用双排桩(约10,m以内[4])或单排桩结合反压土(约8,m以内[6])的支护方案.但随着基坑深度的增大,单纯的无支撑支护手段将无法满足安全与稳定的要求,这时,如果场地条件允许,多级开挖与无支撑支护技术相结合则可以作为一个很好的方案.多级支护技术目前已经在全国各地很多大型项目中得到了很好的应用,例如北京国家大剧院超深基坑工程[10]、上海虹桥综合交通枢纽基坑工程[11]以及天津仁恒海河广场项目基坑等.无支撑多级支护技术综合了多级支护及无支撑支护技术的优点,具有适用于大面积复杂超深基坑、经济性好、便于开挖施工以及节约工期等特点.在实践中,可以在各级支护中根据实际情况选择单排桩、地连墙、双排桩、放坡、重力式挡土墙、反压土等多种无支撑支护形式,进行合理灵活的组合,以达到最为安全经济的效果.虽然在实践上,无支撑多级支护技术已经积累了一定经验,但是其变形受力特点、各级支护相互作用机制、设计理论、稳定评价方法及破坏机理等重要内容都还几乎是空白.这些都极大地限制了这项综合性技术的应用与发展.
本文结合天津某实际工程的基坑,利用有限元方法及物质点法(material point method,MPM)对软土地区的无支撑多级支护基坑的稳定问题进行了探索,得出了一些有关其破坏特点及破坏滑动面开展规律的结论,为继续深入研究这种支护方式的稳定性提供了方法及理论上的参考.
1 MPM简介
MPM属于无单元法(meshless methods)的一种,具有较为强大的大变形计算能力.自从 20世纪 90年代 Sulsky等[12-13]提出这种方法以来,目前 MPM已经被广泛应用于滑坡[14]、挡土墙[14]、爆炸[15]、粮仓[16]、切割[16]等多种大变形工程问题.在MPM中,物体被离散为大量基于拉格朗日描述的物质点,在整个运算过程中,质量、速度、应力及应变等状态变量均由这些物质点储存.每一个时间步,物质点上的状态变量都会传递给背景网格节点(图 1[17]中①→②),在背景网格上进行运动方程的求解(图1中②→③),计算结束后,这些变量再由网格节点重新映射给物质点(图 1中③→④),并且在物质点完成本构增量积分,网格也会重新恢复到原状(图1中④→⑤),准备下1个时间步的运算[17].由 MPM 的运算过程可以发现,与传统的有限元或者有限差分法相比,在 MPM 中,背景网格仅作为运动方程计算的一个工具,而不储存位移、速度等变量信息,因此在大变形计算中不会产生类似有限元法(finite element method,FEM)及有限差分法(finite difference method,FDM)的网格畸变问题.传统的离散元方法(discrete element method,DEM),例如颗粒流,也是大变形计算的一种工具,但是 DEM在用于解决实际工程问题时,无法直接利用已经较为成熟的本构模型,而只能近似地用大量颗粒来拟合土体或结构的宏观力学特性,一方面使用不方便,另一方面也不够精确. 另外,由于 DEM 中颗粒间的咬合作用,其很难模拟黏性土的不排水力学特性(摩擦角为 0°),而这一点正是模拟软土地区岩土工程稳定问题的关键.相对于 DEM,可以直接利用成熟本构模型的 MPM 更适合解决不排水破坏的稳定问题.
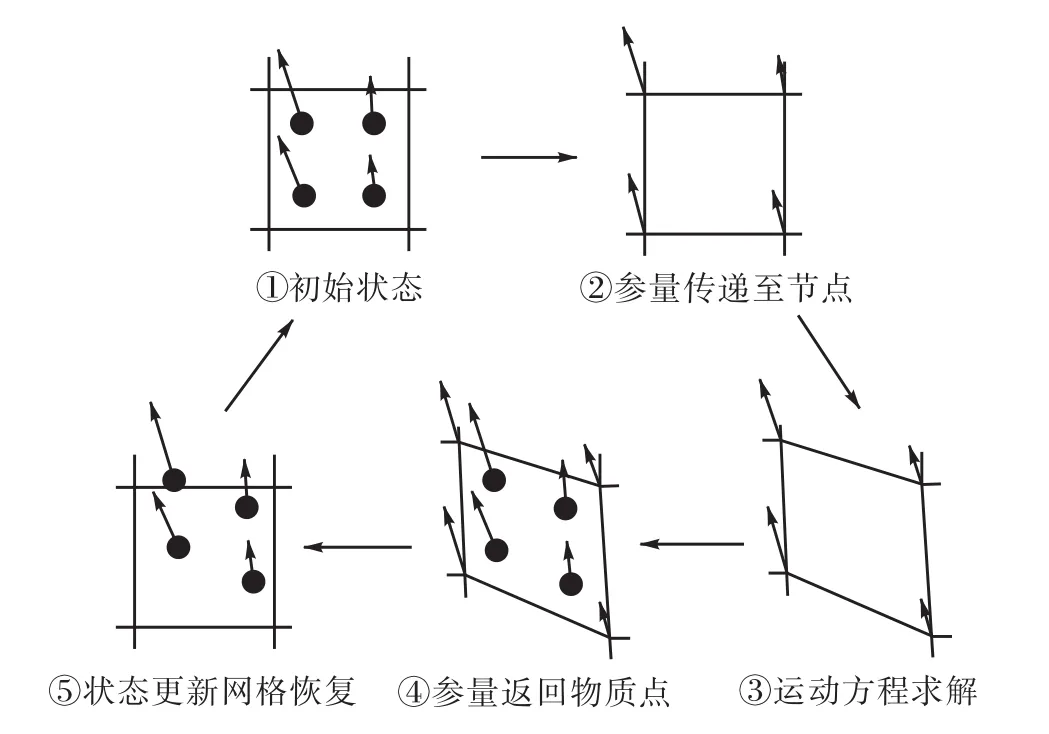
图1 1个时间步内MPM运算步骤示意[17]Fig.1 Illustration of the steps in MPM algorithm in a time step[17]
2 稳定性及破坏面开展机理有限元研究
首先采用传统的有限元法对无支撑多级支护基坑进行研究,同时也为后文MPM的研究结果提供参照与印证.研究内容包括基坑整体稳定性分析、随着开挖深度增加及土体强度降低基坑剪切带开展规律研究等.
2.1 工程概况及有限元模型
图2为天津某基坑的一个剖面,基坑开挖深度为10.8,m;采用两级支护,第1级支护为双排桩,第2级支护为单排灌注桩.以此基坑为原型,为了便于计算分析,对其几何尺寸进行了简化,如图 3所示.有限元模型中,双排桩前后两排桩间距为 4,m,桩长均为25,m,第1级开挖深度为6,m.第1级支护与第2级支护之间的台阶宽度为 5,m.第 2级支护为单排桩,桩长 12,m,开挖深度为 4,m.基坑开挖总深度为10,m,坑外考虑 20,kPa的超载.同样,为了方便分析,模型的土质条件也根据原型进行了简化.考虑到软土地区土体渗透系数较低,并且开挖过程及破坏过程较短,因此本文采用总应力法分析,强度指标采用摩擦角φ=0°的不排水强度cu.模拟中近似假定不排水强度cu(kPa)沿深度线性增加,即

式中z为土体埋深.
由于为不排水分析,因此本应采用不排水泊松比0.5,但是当泊松比为 0.5时,会导致有限元中的刚度矩阵异常,此时可以选择一个较为接近0.5的值来避免异常产生,本文取泊松比为0.495[18].根据经验,软土在不排水压缩时,剪切模量 G可近似取100,cu[19],弹性模量为E=3G.考虑到摩尔-库伦模型无法很好地反映土体在卸载时的回弹变形特性,而软土的回弹模量远高于其压缩弹性模量,因此本文分析中,弹性模量采用压缩弹性模量的 3倍来近似考虑这个问题[20].土体密度取1,900,kg/m3,水平侧压力系数取0.64.桩土界面采用可以相对滑移的接触面单元,其剪切破坏符合Coulomb破坏准则,在此其强度取为0.7倍的土体强度.
有限元模型如图 3所示,模型总长度为 100,m,高度为40,m,共划分1,760个单元,在双排桩及单排桩附近对网格进行了加密.双排桩及单排桩的弹性模量为30,GPa,泊松比0.2,几何参数如图2所示,根据等效原则换算为平面应变模型.模型计算过程中,每步开挖 2,m.开挖到底后,利用有限元强度折减法对基坑进行安全系数计算.

图2 天津某工程支护结构剖面Fig.2 Profile of the retaining structures of a project in Tianjin
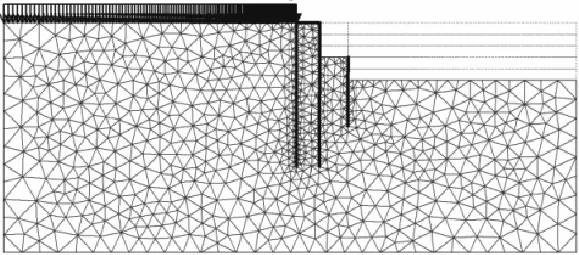
图3 有限元模型及网格Fig.3 Finite element model and mesh
2.2 有限元计算结果及强度折减法稳定性分析
开挖到基坑底,即 10,m 深时,基坑水平位移云图如图 4所示.基坑位移整体上类似于悬臂支护结构,但是又有所不同:双排桩的前桩由于后桩通过连系梁对其的约束作用,最大位移不在桩顶,而在桩顶下 5,m左右.双排桩前排桩的最大水平位移为44.56,mm,后排桩为43.06,mm,单排桩为44.54,mm,两级支护结构的位移较为接近,从这一点可以初步看出两级支护结构具有一定整体性.
根据有限元强度折减法计算,此基坑的整体稳定安全系数为 1.494.基坑破坏后网格变形与原网格的对比及塑性点的分布分别如图 5和图 6所示.从这两幅图可以大致看出基坑破坏后的形态、影响范围及滑动面形状.但是有限元强度折减法是以计算不收敛作为破坏准则的,而传统有限元在大变形计算时,网格畸变严重,其计算得到的破坏后的形态及变形大小往往很不可靠,所以在对其破坏后的形态及影响范围进行具体分析时,采用具有大变形计算能力的MPM(见第 3节).在此,仅对双排桩与单排桩组合两级支护基坑破坏特点作定性分析.

图4 开挖完成后基坑水平位移云图Fig.4 Contour of horizontal displacement after excavation
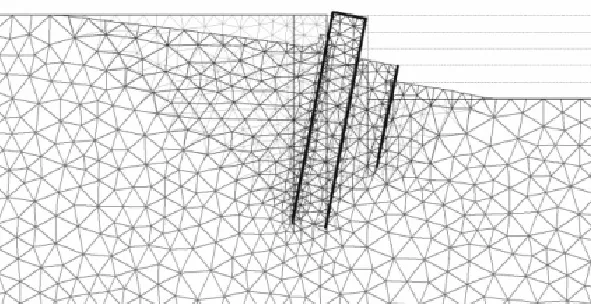
图5 基坑破坏前后网格对比Fig.5 Comparison of mesh before and after collapse
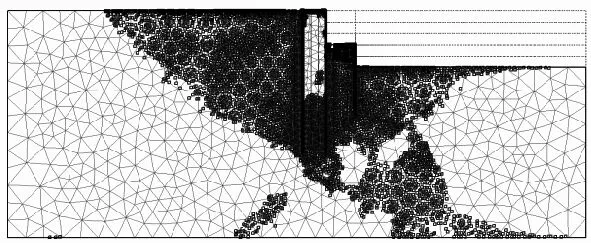
图6 基坑破坏后塑性点分布Fig.6 Distribution of plasticity points after collapse
由图5及图6可以看出,此两级支护基坑失稳破坏滑动面为圆弧形,破坏形态整体上接近悬臂支护的基坑,整个支护结构向坑内倾覆.基坑失稳后,坑外土体下沉,坑内土体隆起,坑内外网格均产生较大的变形.但是单排桩的最终形态几乎平行于双排桩,它们之间的土体网格未见有明显变形,这说明此两级支护及其内部土体形成了一个较为稳定的整体,从而使得整个支护体系具有较大的宽度,具有更强的抗倾覆能力.
2.3 剪切塑性区域随开挖深度的开展分析
剪切塑性区域的开展分两个角度研究:①随着开挖的不断进行、基坑深度的逐渐增加,剪切带的开展情况;②同样开挖深度,随着基坑土体强度的变化,剪切塑性区域的变化情况.下文对第1种情况进行分析.
根据前文强度折减法计算,此基坑的稳定安全系数为 1.494,在这个安全系数下,基坑开挖产生的剪切塑性带开展不明显,不利于研究.因此,将此基坑土体强度进行折减,使其安全系数为 1.01,这时土体的不排水强度为 cu=12.17+2.37,z (kPa),如果强度再降,基坑在开挖到底时计算将很难收敛.图 7~图11分别是此安全系数为1.01的基坑在开挖到不同深度时的剪切应变等值线云图.为了更明确地看出剪应变随开挖深度的开展情况,对剪应变云图的显示范围进行了统一,其显示范围均为0~1.6%,图例相同.
由图7可以看出,开挖2,m时,剪切应变在双排桩后,从桩顶沿斜下方开展,这是由于双排桩向坑内位移引起的;由于双排桩的挤压,其被动区的上部也有一定的剪切应变开展,但数值较小.总体来讲,开挖 2,m 时剪应变值很小,最大值仅为 0.21%,主要集中在双排桩后由桩顶开始的倾斜方向.

图7 开挖2,m时剪应变云图Fig.7 Contour of shear strain when excavation depth is 2,m
由图8可以看出,开挖4,m时,双排桩主动区沿桩顶斜向发展的剪应变区逐渐增大,并向双排桩一侧发展.双排桩被动区的剪应变也继续扩大.另外,双排桩两根桩的桩尖均有倾斜方向的剪切带产生,但应变值还较小.过桩底倾斜延伸到坑外地面的剪切带和剪切区域也有所显现,但仍不明显.开挖 4,m 时,应变最大值仅为0.74%.

图8 开挖4,m时剪应变云图Fig.8 Contour of shear strain when excavation depth is 4,m
如图9所示,开挖6,m时,上述区域的应变范围和应变值均继续发展,最大剪应变值达到 1.57%.双排桩主动区过桩底延伸到坑外地面的圆弧形剪切应变带清晰可见.另外,这个阶段发展较为明显的是,双排桩中位于基坑内侧的桩,其桩底处斜向剪切带发展迅速,说明此桩对其下部土体挤压严重.这从侧面反映了双排桩类似于重力式挡土墙倾覆破坏沿内侧墙角旋转的特征.这个结果也验证了文献[4]中双排桩内侧桩底部土体抗压从而设置弹簧的假设.

图9 开挖6,m时剪应变云图Fig.9 Contour of shear strain when excavation depth is 6,m
开挖完6,m后,开始在单排桩内部进行开挖.如图 10所示,开挖到 8,m 深时,最大剪应变值达到3.30%,剪应变除了在上述区域继续发展外,较为明显的特征是,双排桩被动区的剪切带不再发展,剪切带改在单排桩被动区开展.这说明由于单排桩的支护,双排桩被动区的土体变形减小,剪切带发展受到抑制,发生塑性屈服的速度减缓,从而为双排桩的稳定提供了足够的被动土压力,增加了主要支护结构的稳定性,减小了坑外土体变形.上述现象从剪切带发展角度揭示了单排桩与双排桩两级支护的共同作用机理.

图10 开挖8,m时剪应变云图Fig.10 Contour of shear strain when excavation depth is 8,m
如图 11所示,当开挖到坑底,即 10,m 深时,最大剪应变值达到 28.40%,沿双排桩外侧桩桩底延伸到坑外地面的剪切带及坑内单排桩被动区由桩底到坑底的剪切带完全形成.同时,在双排桩内侧桩桩底以下的挤压剪切区域也在逐渐扩大,在双排桩被动区底部附近也形成了一个剪切区域,此时,这些剪切区域还未完全贯通,因此基坑还处于稳定状态,可以预见,这些剪切区域如果继续发展,会逐渐将坑内和坑外的两条主要剪切带联系贯通,那时基坑就会发生沿剪切区域边缘的整体滑动破坏.但是,在图 11中可以发现,即使在安全系数仅有1.01的基坑中,此两级支护结构内部土体,即双排桩内部及双排桩与单排桩之间的土体,剪应变范围及量值与其他区域相比也均非常有限,表现出非常良好的稳定性,避免了支护体系首先从内部破坏,使得整个支护体系形成一个有机整体,共同抵抗倾覆及失稳破坏的发生.
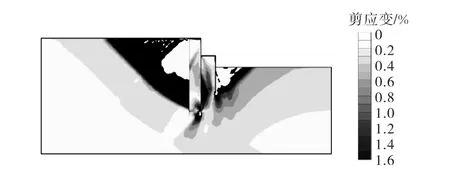
图11 开挖10,m时剪应变云图Fig.11 Contour of shear strain when excavation depth is 10,m
另外,在边坡失稳中,通常是通过坡脚形成一个发展到坡顶后方的圆弧形剪切带,而滑动体内部剪切变形发展较小,无明显剪切区域开展,滑动体类似于一个刚性体整体滑下[21],如图 12[21]所示.但是,在基坑中,通过对剪切区域的发展分析及图 11可以发现,由于支护结构的存在,剪切区域的开展更加复杂,最终滑动体内部也发生了较大的剪切应变.由此可见,与边坡相比,基坑工程中的失稳破坏机理更加复杂,更需要进行深入研究.只有掌握了其破坏机理,才能有的放矢,进而研究得出控制基坑破坏发展的理论.
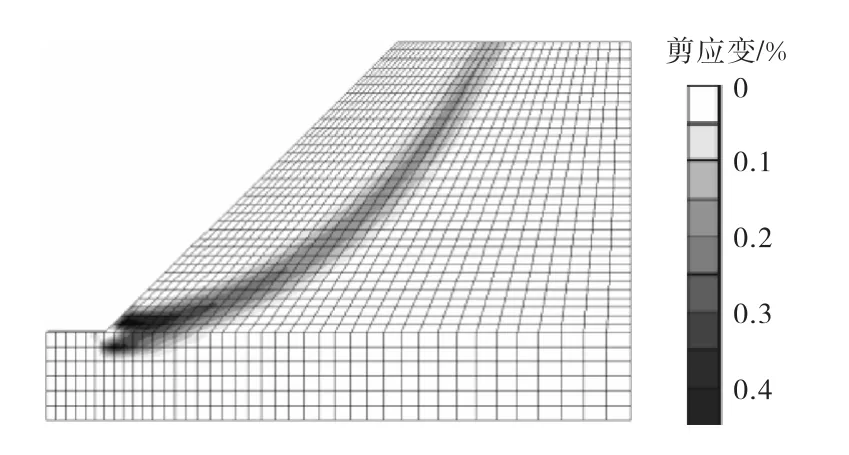
图12 边坡中剪应变云图Fig.12 Contour of shear strain in slope
2.4 剪切塑性区随土体强度的变化分析
类似于强度折减法,通过逐渐改变土体强度,也可以对基坑的变形及剪切区域的开展进行研究.本文计算了如表1所示的8种不同安全系数的基坑.图13为基坑的最大水平位移相对于安全系数的变化曲线.由此可以发现,随着基坑安全系数的降低,基坑位移逐渐增加,且安全系数越小,位移增加速度越快,在安全系数接近1时,位移急剧增加,几乎无法收敛,说明基坑已经接近极限状态.图14为不同安全系数情况下基坑剪应变云图,为了便于观察对比,对每种工况的剪应变显示范围进行了归一化,各个图中剪应变的显示范围均为 0~3.000%.由图14可以清楚地观察出当强度逐渐降低时剪切带的发展情况.首先双排桩后主动区剪切带从桩顶开始逐渐斜向下发展,长度与宽度均逐渐增大,当土体降低到一定程度时,在这条剪切带的垂直方向出现了两条剪切带,内侧一条通过桩底逐渐延伸到坑外地面,外侧剪切带一直处于次要地位,剪切应变值较小,内侧的剪切带逐渐与其内部不断扩大的剪切区域贯通形成一个整体的剪切破坏区域.单排桩被动区的剪切区域逐渐扩大,最终形成一个过桩底的三角形剪切破坏区域.双排桩及单排桩中间的土体由于单排桩的支护作用,剪切应变的开展一直较为有限,仅在接近破坏时,双排桩底部附近才产生一个稍大的剪应变区域.双排桩两根桩底部均有斜向剪切带向下发展,其中坑内侧桩底剪切带发展得更为充分,说明双排桩及其内部土体整体绕此桩底转动的特性.剪切带随土体强度的变化规律基本上与随基坑深度变化的规律类似.

表1 不同安全系数情况及其对应的不排水强度(工况1~8)Tab.1 Safety factors and corresponding undrained strengths(work condition 1—8)

图13 不同安全系数下的基坑最大水平位移Fig.13 Maximum horizontal displacements for different safety factors
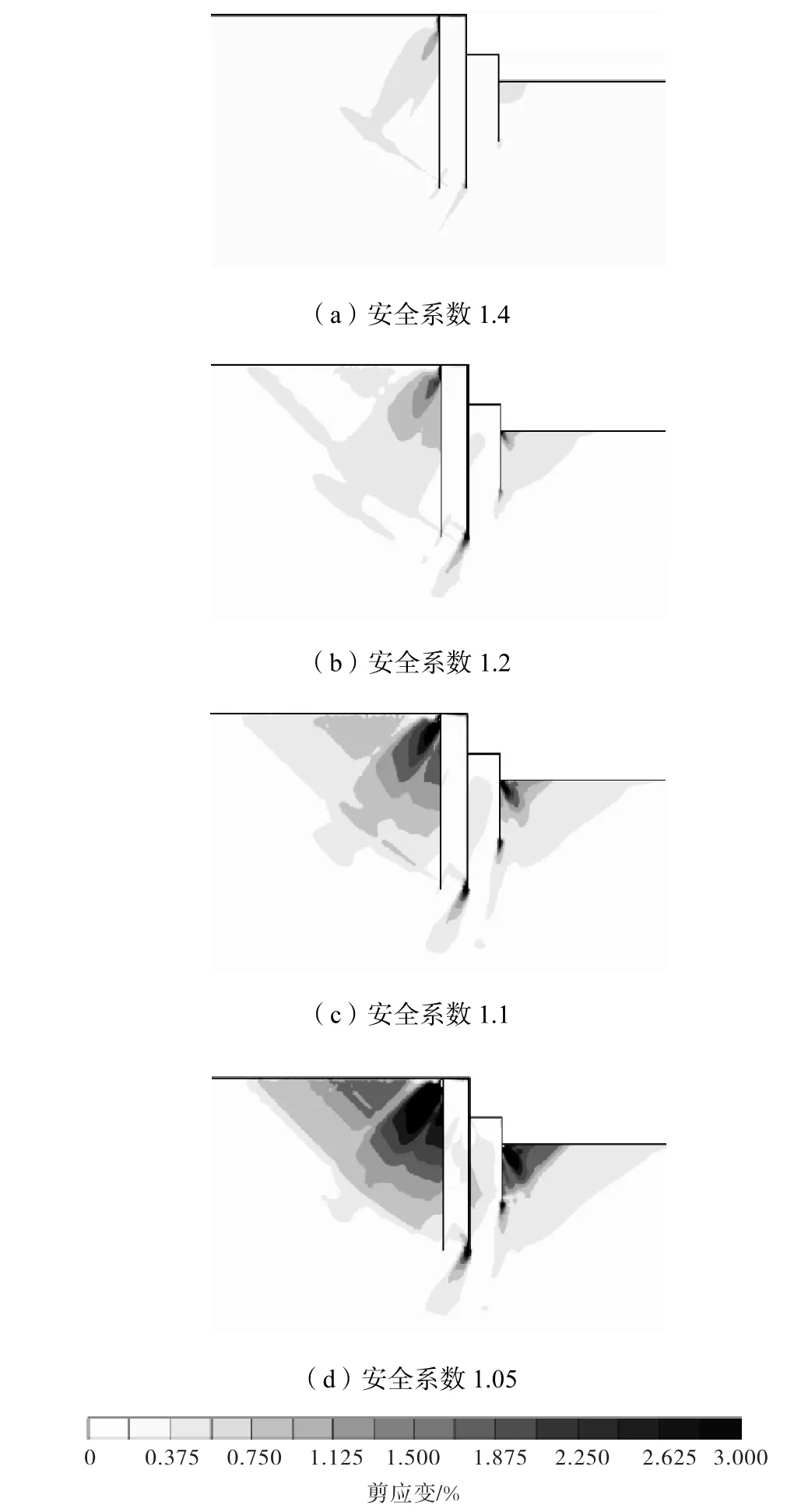
图14 不同土体强度时剪应变云图Fig.14 Contour of shear strain at different soil strengths
2.5 桩间加固对支护体系稳定性影响分析
由上文分析可知,在两级支护的双排桩与单排桩间距为 5,m的情况下,两级支护结构类似于一个整体的重力式挡墙协同工作来抵抗失稳破坏.为了验证这个观点,进行了如下模拟:将双排桩内部及单排桩与双排桩之间的土体进行搅拌桩加固,如图 15中1、2区域,使此两级支护结构形成一个重力式挡墙,对比加固后与加固前的稳定性与滑动面开展机制.加固土体的物理力学参数为:黏聚力 100,kPa,摩擦角0°,弹性模量1,GPa,泊松比同样采用0.495.

图15 加固后开挖10,m时剪应变云图Fig.15 Contour of shear strain when excavation depth is 10 m after ground improvement
经过计算,开挖到 10,m 时,支护结构最大水平位移为 33.26,mm,较未加固前的 44.56,mm降低25.36%.可以发现,桩间加固对变形控制的作用还是非常明显的.经过有限元强度折减法计算,加固后安全系数为 1.538,比未加固前的 1.494提高了2.95%.图 15为加固后安全系数为 1.04的基坑开挖到底时的剪应变云图.由图可知,由于加固区土体强度高、刚度大,因此在开挖到底后剪应变几乎可以忽略.对比图14(d)与图15可以发现,双排桩主动区与单排桩被动区的剪切塑性区很接近;不同的是,图 15中,双排桩内侧桩底部的挤压塑性区不再明显,而单排桩底部出现了较大的挤压塑性区,说明整个支护体系绕单排桩底部转动,对单排桩底部土体挤压严重.这一点,与未加固前有些区别.但总体来讲,加固前后剪应变开展情况类似,滑动面长度未有明显变化,因此加固对整体稳定性的提高贡献很小,仅使安全系数提高了 2.95%.由以上分析可知,此两级支护结构在未加固前已经具有了较强的整体性.当然,此结论是针对本文特定的两级支护基坑,是在双排桩与单排桩间距有限的情况下得出的,当两者的间距过大时,两级支护间的协同工作机制将会发生变化,这一点还需继续研究.
3 MPM稳定破坏计算分析
本节采用具有大变形计算能力的方法 MPM 来进行多级支护结构稳定性及破坏过程分析.MPM 模型的支护结构尺寸与PLAXIS模型相同,土体参数也一致,考虑到基坑破坏后影响范围比有限元计算中没有破坏时的情况要大,因此对 MPM 模型进行了加大,整个模型长为120,m,高度仍为40,m,如图16所示.模型中土体及结构物均由颗粒组成,共有 17,040个,背景网格间距为1,m×1,m,初始状态下每个网格包含 4个颗粒.双排桩外同样有 20,kPa的超载.桩体的宽度均为 1,m,通过抗弯刚度等效与实际情况相对应,等效后,双排桩的弹性模量为 8.28,GPa,单排桩的弹性模量为 3.03,GPa.MPM 计算方法能自动处理没有相对滑动破坏的接触面[12-13],但是相对滑动的情况还需要引进适当的接触算法,本文采用的 MPM程序还没有接触面模块,因此在桩土接触面上 MPM模型还是与有限元模型略有不同.

图16 MPM多级支护基坑模型Fig.16 MPM model of multi-stage retaining structure
3.1 变形及破坏影响范围分析
本文共计算了不同土体强度下的 16种工况,包括表1中的8种工况及表2中的8种工况,表2中的安全系数及其对应土体强度均是以有限元强度折减法得到的安全系数结果 1.494及其对应土体强度按安全系数比例计算得到.如图 13所示(图中安全系数是基于有限元结果,下同),在小变形情况下(例如安全系数大于1.1时),MPM变形计算结果与有限元计算结果较为接近,但是有一定差别,MPM 结果总体比有限元大 25%左右.存在差别的原因主要是MPM 计算为一步开挖,并没有分步开挖,因此变形会比有限元分步开挖时大.图13中,安全系数为1.0时为有限元计算结果的临界极限状态,而MPM结果略有不同,在安全系数约小于0.9时,位移急速增长,趋于失稳.这时则可认为工况 1中基坑(初始工况)采用 MPM 计算得到的安全系数约为 1.494÷0.9=1.660,与有限元强度折减法计算结果也较为接近.由以上结果可以看出,由于MPM的大变形计算优势,能够研究超出常规有限元计算范围的工况,有利于设计及研究人员更好地判断估计基坑的变形,甚至破坏情况.MPM也可以采用类似于强度折减法的方式来得到基坑的安全系数,但事实上,如今在设计中,变形控制理论正逐步成为趋势,因此大变形计算得到的变形结果比单纯的安全系数更直观,也更有意义和价值.
即使在基坑发生大变形破坏的情况下,MPM 计算结果也可以直观地给出基坑稳定后的形态、变形大小及影响范围,这是常规有限元较难得到的结果.图17所示为基坑在工况 14~16情况下发生明显大变形破坏后的状态.由图可见,随着土体强度的降低,基坑的破坏程度越来越严重.从基坑破坏后的变形可以看出,坑外土体由于支护结构向坑内倾覆而沉陷,坑内土体则由于受挤压而隆起.虽然基坑有两级,但是由于两级支护结构间距较小,整个支护结构的破坏状态仍与单级的悬臂支护结构接近.破坏后,双排桩与单排桩仍保持平行状态,再次说明其作为一个整体来抵抗破坏的发生.总体来讲,MPM 得到的破坏形态与有限元得到的结果类似.不同的是,在有限元结果中,如图 5及图 11所示,双排桩及单排桩之间的土体还未发生较大变形,剪切应变也较小,但是在MPM计算结果中,如图17所示,由于基坑变形较大,这部分土体也已经产生严重破坏,发生了很明显的剪切变形.MPM 大变形计算更完整地反映出了多级支护失稳破坏的发展过程与特点.
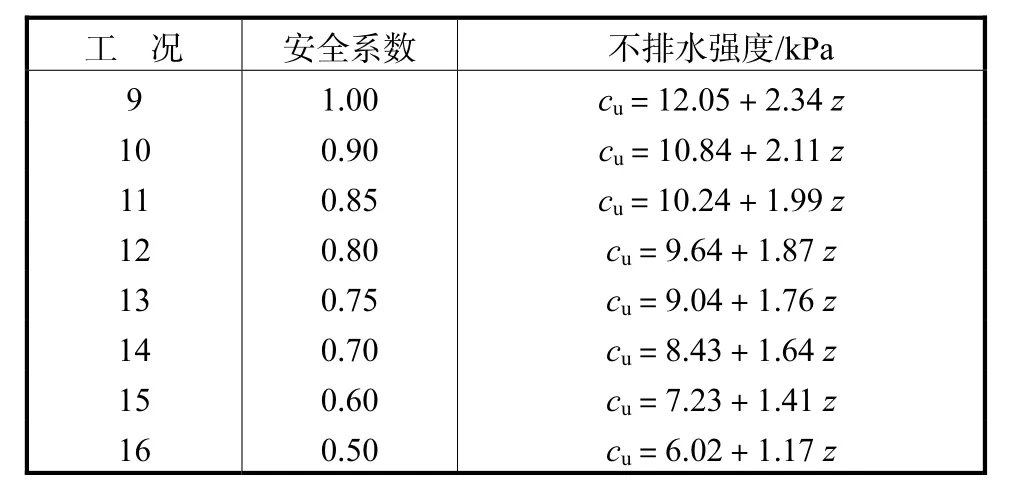
表2 不同安全系数情况及其对应的不排水强度(工况9~16)Tab.2 Safety factors and corresponding undrained strengths(work condition 9—16)
图18为大变形情况下(安全系数小于1.0),基坑变形,包括最大水平位移、坑外沉降及坑内隆起随土体强度变化曲线.由图可见,水平位移最大,坑外沉降次之,坑内隆起最小,并且随着土体强度的降低,变形发展的速度越来越快,说明基坑土体的塑性区越来越大,塑性流动程度加剧.图 19为坑外沉降及坑内隆起影响较严重的区域大小(在此定义沉降或隆起大于10,cm时为影响严重),在安全系数为0.5时,沉降及隆起大于10,cm的范围均已超出了模型边界,因此未在图中给出具体数值.由图 19可知,坑外沉降的影响范围比坑内隆起大 10,m左右,基坑发生破坏后的影响范围与土体强度相关.当安全系数不足时,基坑的破坏范围可能非常大,例如,虽然此基坑仅有10,m深,但是受其严重影响的区域会达到 60,m以上.
一般研究表明,在小变形时,基坑坑外沉降的范围为2~4倍基坑深度[21-22],而传统极限平衡法(简单条分法、Bishop法等)、极限分析法或者有限元强度折减法也都只能针对某一特定基坑给出一个安全系数及其对应的破坏滑动面,而这些方法都无法准确预测基坑破坏时的影响范围.而大变形计算软件在基坑稳定性研究中的应用将会解决这个问题,其可以计算出基坑在各种真实或者假定情况下的基坑破坏情况,例如土体强度不足、坑外超载、支护结构破坏、土体降雨软化等,计算得到的破坏变形及影响范围等结果将为设计、研究、施工甚至是决策人员提供参考,帮助其改进设计方案、制定险情预防或应急措施、确定疏散范围、预估破坏程度等.

图17 不同工况下基坑的破坏情况及水平位移等值线Fig.17 Collapse states and horizontal displacement contours under different work conditions
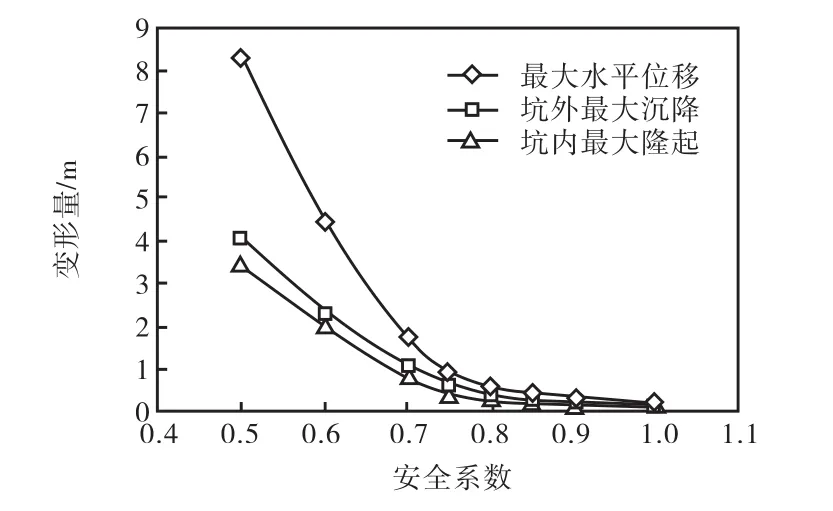
图18 不同安全系数下的基坑大变形情况Fig.18 Large deformations for different safety factors
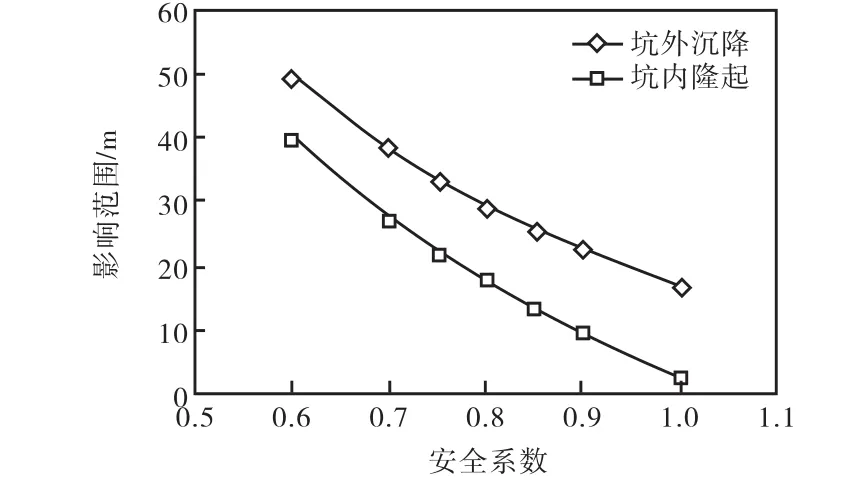
图19 不同安全系数下的基坑变形影响范围Fig.19 Influence areas of large deformations for different safety factors
3.2 剪切滑动面开展分析
图20为工况 16在失稳破坏的各个阶段的剪应变云图.图中颜色最深的区域为剪应变大于或等于15%的位置,当剪应变大于 15%后未对不同应变梯度进行颜色区分,这样做是为了更直观地观察出重点研究区域剪应变的相对大小及开展过程,否则某些应变局部化严重的位置由于应变过大将影响其他区域的显示.在图 20(a)中可以发现,由于桩土界面未采用可以滑移的接触面模型,因此在基坑变形后,桩土界面附近的土体由于较大的桩土相对变形而产生非常大的剪应变,例如双排桩的主被动区及单排桩的被动区均有应变集中的现象.这一点与实际情况是有差别的,也是本次 MPM 模拟的一个缺陷,需要在今后的研究中继续改进,在程序中引入接触面模型.
忽略桩土界面附近应变集中化的位置,可以发现,在变形较小时MPM模拟结果中剪应变的开展与有限元结果接近.如图 20(a)所示,剪应变区域在双排桩主动区从双排桩顶开始斜向发展,主要发展区域靠近双排桩一侧,在单排桩被动区从坑底开始斜向发展,主要发展区域靠近单排桩一侧,如图中虚线所示位置及其内部区域,这时由于变形相对较小,应变值也较小,还未能观察到较为明显的主被动区滑动面.如图 20(b)所示,基坑变形较上一阶段增大,两个主要剪应变塑性区域也继续扩大,双排桩与单排桩之间的土体由于受到剪切和挤压已产生较明显的塑性变形,基坑主动区和被动区的滑动面初步显现,如图中点划线所示,但仍不明显.如图 20(c)所示,这一阶段由剪应变云图轮廓已经可以观察出较明显的剪切滑动面,如图中点划线所示,基坑主动区滑动面自双排桩外侧桩底延伸到坑外地面,被动区滑动面自双排桩内侧桩底延伸到坑底.双排桩内侧桩底产生了一定的挤压塑性区,另外结合图 17中双排桩底附近位移很小的情况,说明基坑整体绕双排桩内侧桩底倾覆,而单排桩作为次级支护结构,由于其桩底位于整体稳定滑动面以上,因此随双排桩被动区土体一起移动.这一阶段的塑性区及剪切滑动面特征已显现出与小变形时的不同.在图 11中,当双排桩主动区及单排桩被动区滑动面贯通,基坑即达到极限状态,而事实上,当基坑继续破坏时,基坑被动区的滑动面会由单排桩桩底向下移动到双排桩桩底.这一点进一步说明了大变形计算更完整地反映了多级支护基坑失稳破坏的过程.随着破坏的继续发展,如图 20(d)及(e)所示,变形和塑性区域逐渐扩大,滑动面也进一步向外扩展,直到基坑土体及支护结构达到新的平衡状态.

图20 工况16中剪切塑性区的开展过程Fig.20 Propagation process of the shear plastic zone in work condition 16
在传统的极限平衡法或极限分析法求解边坡或基坑的整体稳定安全系数时,当其土体强度成比例变化而其他条件不变时,计算出来的安全系数会成比例变化但是最危险的滑动面却仍保持不变.但观察图17及图20(e)和图21即可发现,当强度变化后,最终破坏后的状态及剪切滑动面是不同的.与第2.1节中的结论类似,传统方法很难预测出真实破坏后的影响范围及最终滑动面,而大变形计算方法则解决了这个问题.

图21 工况15破坏状态及剪切滑动面Fig.21 Collapse state and shear slip surface in work condition 15
3.3 无支撑两级支护结构破坏全过程分析
综合小变形及大变形分析可以看出,当双排桩及单排桩组合的两级支护结构在安全系数足够、变形较小时,两级支护结构作为一个整体共同维护基坑平衡,塑性区主要在双排桩主动区、单排桩被动区及双排桩内侧桩底开展,两级支护之间的土体由于次级支护结构单排桩的支挡而使剪切塑性区开展得到了有效限制,从而也保证了主要支护结构双排桩的变形与稳定,两级支护结构在此阶段表现出很好的协同工作机制;而当基坑安全系数不足、发生稳定破坏时,两级支护间的土体由于较大的挤压及剪切也进入塑性阶段,同时单排桩被动区的剪切区域也扩大到整个双排桩被动区,次级支护结构单排桩由于周围土体均进入塑性阶段而几乎失去支护作用,从而随着双排桩被动区土体一起流动.
4 结 论
(1) 双排桩与单排桩组合的无支撑两级支护基坑在两级支护间距有限的情况下,失稳特点为:整体上类似于悬臂厚挡墙的倾覆破坏,整个支护结构绕双排桩内侧桩桩底旋转;共同作用机制为:次级支护结构单排桩支挡了两级支护间的土体,使其变形及塑性区开展均得到有效限制,由此保证了主要支护结构双排桩的稳定,使得整个支护体系有了较大的支护宽度,增强了基坑的稳定性.从上述特点可以看出,在无支撑多级基坑中,如果支护方案合理,各级支护结构之间具有很好的协同工作能力,能够作为一个整体共同抵抗变形及失稳破坏,可以很好地完成软土地区大面积深基坑的支护任务.
(2) 传统有限元方法和大变形计算方法 MPM的综合运用,完整地分析了基坑在整个破坏过程中的剪切破坏面发展过程:在基坑达到极限状态之前,塑性区主要在双排桩主动区、单排桩被动区及双排桩内侧桩底开展,随后自双排桩桩底及单排桩底在坑内外形成两条延伸到地面的圆弧形滑动面,当这两条主要滑动面贯通后,基坑达到临近破坏的极限状态.随着变形的继续增大,两级支护间土体开始破坏,单排桩被动区的圆弧形滑动面下移到双排桩桩底,单排桩也随屈服的土体一起运动,两级支护的共同作用机制失效.当破坏继续进行、塑性区持续扩大时,圆弧滑动面也动态向外扩张,直至达到新的平衡状态.
(3) 大变形计算方法 MPM 可以直观地给出基坑破坏后的形态.由 MPM 计算结果可知,当土体强度降低时,基坑的破坏影响范围及最终滑动面会逐渐增大.而传统方法只能针对一个基坑给出某个特定的滑动面,很难预测出基坑破坏后的实际影响范围及最终滑动面.此次无支撑多级支护结构稳定性的研究初步验证了大变形计算软件 MPM 在基坑破坏研究中的优势,为基坑稳定性研究提供了新的思路及方法.不过目前 MPM 的发展尚不够完善,需要进一步研究与开发.
致 谢:
本文采用的 MPM 计算程序属于剑桥大学工程系,开发者为 Kenichi Soga教授、Samila Bandara博士和 Krishna Kumar博士等.笔者为了进行本次研究,在剑桥大学MPM源程序的基础上做了一些二次开发工作,工作过程中同样得到了他们的指教.在此对Kenichi Soga教授、Samila Bandara博士和Krishna Kumar博士对本文的支持和帮助表示衷心感谢.
[1] 史海莹. 双排桩支护结构性状研究[D]. 杭州:浙江大学建筑工程学院,2010.Shi Haiying. Study on the Behavior of Double-Row Piles[D]. Hangzhou:School of Civil Engineering,Zhejiang University,2010(in Chinese).
[2] 何颐华,杨 斌,金宝森,等. 双排护坡桩试验与计算的研究[J]. 建筑结构学报,1996,17(2):58-66.He Yihua,Yang Bin,Jin Baosen,et al. A study on the test and calculation of double-row fender piles[J]. Journal of Building Structures,1996,17(2):58-66(in Chinese).
[3] 蔡袁强,赵永倩,吴世明,等. 软土地基深基坑中双排桩式围护结构有限元分析[J]. 浙江大学学报:自然科学版,1997,31(4):442-447.Cai Yuanqiang,Zhao Yongqian,Wu Shiming,et al.FEM analysis of the deep pit excavation with retaining structure of the double piles in soft clay[J]. Journal of Zhejiang University:Natural Science,1997,31(4):442-447(in Chinese).
[4] 郑 刚,李 欣,刘 畅,等. 考虑桩土相互作用的双排桩分析[J]. 建筑结构学报,2004,25(1):99-106.Zheng Gang,Li Xin,Liu Chang,et al. Analysis of double-row piles in consideration of the pile-soil interaction[J]. Journal of Building Structures,2004,25(1):99-106(in Chinese).
[5] 刘 钊. 双排支护桩结构的分析及试验研究[J]. 岩土工程学报,1992,14(5):76-80.Liu Zhao. Analysis and experimental investigation of double-row piles structure[J]. Chinese Jounal of Geotechnical Engineering,1992,14(5):76-80(in Chinese).
[6] 郑 刚,陈红庆,雷 扬,等. 基坑开挖反压土作用机制及其简化分析方法研究[J]. 岩土力学,2007,28(6):1161-1166.Zheng Gang,Chen Hongqing,Lei Yang,et al. A study of mechanism of earth berm and simplified analysis method for excavation[J]. Rock and Soil Mechanics,2007,28(6):1161-1166(in Chinese).
[7] Powrie W,Daly M P. Centrifuge model tests on embedded retaining walls supported by earth berms[J]. Geotechnique,2002,52(2):89-106.
[8] 李顺群,郑 刚,王英红. 反压土对悬臂式支护结构嵌固深度的影响研究[J]. 岩土力学,2011,32(11):3427-3436.Li Shunqun,Zheng Gang,Wang Yinghong. Influence of earth berm on embedment depth of cantilever retaining structure for pit excavation[J]. Rock and Soil Mechanics,2011,32(11):3427-3436(in Chinese).
[9] 包旭范,庄 丽,吕培林. 大型软土基坑中心岛法施工中土台预留宽度的研究[J]. 岩土工程学报,2006,28(10):1208-1212.Bao Xufan,Zhuang Li,Lü Peilin. Study on mound width remained during the construction of central island for large foundation pits in soft soils[J]. Chinese Journal of Geotechnical Engineering,2006,28(10):1208-1212(in Chinese).
[10] 陈 新. 国家大剧院超深基坑支护施工技术[J]. 施工技术,2005(增):33-37.Chen Xin. Construction technology of super deep foundation pit support of the National Great Theater project[J]. Construction Technology,2005(Suppl):33-37(in Chinese).
[11] 翁其平,王卫东. 多级梯次联合支护体系在上海虹桥综合交通枢纽基坑工程中的设计与实践[J]. 建筑结构,2012,42(5):172-176.Weng Qiping,Wang Weidong. Design and construction of multi-level supporting system for deep foundation pits excavation of Shanghai Hongqiao Integrated Transport Hub[J]. Building Structure,2012,42(5):172-176(in Chinese).
[12] Sulsky D,Chen Z,Schreyer H L. A particle method for history-dependent materials[J]. Computer Methods in Applied Mechanics and Engineering,1994,118(39/40/41):179-196.
[13] Sulsky D,Zhou S,Schreyer H L. Application of a particle-in-cell method to solid mechanics[J]. Computer Physics Communications,1995,87(1/2):236-252.
[14] Vermeer P A,Beuth L,Benz T. A quasi-static method for large deformation problems in geomechanics[C] //The 12th International Conference of International Association for Computer Methods and Advances in Geomechanics(IACMAG). Geo,India,2008:55-63.
[15] Banerjee B. Material point method simulations of fragmenting cylinders[C]//17th ASCE Engineering Mechanics Conference(EM2004). Newark,USA,2004:1-15.
[16] Wieckowski Z. The material point method in large strain engineering problems[J]. Computer Methods in Applied Mechanics and Engineering,2004,193(39/40/41):4417-4438.
[17] Bigler J,Guilkey J,Gribble C,et al. A case study:Visualizing material point method data[C]// Eurographics/IEEE-VGTC Symposium on Visualization. Lisbon,Portugal,2006.
[18] Plaxisbv. PLAXIS 2D 2011 Material models manual[EB/OL]. http://www.plaxis.nl/files/files/2D2011-3-Material-Models.pdf,2012-12-27.
[19] Ladd C. Stress-strain modulus of clay in undrained shear[J]. Journal of the Soil Mechanics and Foundations Division,1964(SM5):103-131.
[20] 陈育民,徐鼎平. FLAC/FLAC3D 基础与工程实例[M]. 北京:中国水利水电出版社,2009.Chen Yumin,Xu Dingping. FLAC/FLAC3D Foundation and Engineering Examples[M]. Beijing:China Water Power Press,2009(in Chinese).
[21] 郑 刚,焦 莹. 深基坑工程:设计理论及工程应用[M]. 北京:中国建筑工业出版社,2010.Zheng Gang,Jiao Ying. Deep Excavation Engineering:Design Theory and Engineering Applications[M].Beijing:China Architecture and Building Press,2010(in Chinese).
[22] PeckR B. Deep excavation and tunneling in soft ground[C]// Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering.Mexico City,Mexico,1969.
