基于SURE无偏估计的图像自适应稀疏收缩去噪

沙正虎，余 剑，崔 琛，2

1.解放军电子工程学院 信息工程系，合肥 230037

2.安徽省电子制约技术重点实验室，合肥 230037

图像在摄取或传输过程中容易受到噪声的污染，从而影响图像信息的提取，因此，去噪是图像处理技术的重要组成部分。图像去噪既要尽可能去除噪声分量，又要尽可能保留图像的细节成分，如纹理和边缘，而各种图像去噪其实就是在去除噪声和保留细节之间进行权衡。为了克服这个问题，Donoho和Johnstone提出了小波收缩法[1]，利用收缩函数对图像小波域系数有选择性地进行取舍，以达到去噪的目的。自此以后，无论是在正交基变换（如小波等），还是紧框架变换（如脊波、曲波等），收缩都成为最常用的去噪算法。目前，收缩主要的研究方向集中在两点：一是收缩曲线的选择，常用的有硬阈值和软阈值两种；另一点则是阈值的选取问题。对于阈值的选取，目前主要有Visu通用阈值[2]、MiniMaxi阈值[3]、SURE阈值[4]（Stein Unbiased Risk Estimator，SURE）等。在上述阈值中，Visu通用阈值（，σ为标准方差，N为信号长度）计算简单，但其趋向于“过扼杀”变换系数，从而会导致过多的高频信息流失；MiniMaxi阈值，由于基于悲观决策的思想，即最大均方误差最小化，所以也会过扼杀现象；SURE阈值估计是一种基于Stein无偏风险估计准则的阈值选择，该准则是均方差准则的无偏估计，趋近于理想阈值。

近几年，稀疏表示作为信号处理领域一个新的工具，越来越引起人们的重视。由于图像本身是稀疏的，所以利用稀疏表示来处理图像具有极大的优越性。传统的小波变换（Wavelet）能够表示图像的点状奇异特征，但对高维信息表示能力不足；Donoho等学者提出的多尺度几何变换[5]，主要有 Rideglet、Curvelet、Contourlet、Bandlet等变换，这些变换充分考虑了图像的某些几何特性，能比小波变换更好地捕捉图像的边缘等奇异特性，但每种变换只能对应某些特征表示是稀疏的；图像的稀疏表示，则是用超完备字典取代传统中的正交基或紧框架来表示图像，而字典的这种冗余性恰恰能够更好地刻画图像的各种奇异特性，且可以同时表示多种奇异特性。

针对以上问题，本文研究了稀疏框架下收缩去噪问题，提出一种基于SURE无偏估计的自适应阈值选择算法（Adaptive SURE，AdpSURE）。本文算法首先推导稀疏框架下收缩去噪的SURE无偏估计目标函数，然后利用黄金分割法搜索全局最小值点，对应的阈值即为自适应选择的阈值。仿真结果验证了本文算法的优越性。

1 图像的稀疏表示

1.1 稀疏表示

自1991年Mallat和Zhang[6]提出匹配追踪算法（Matching Pursuit，MP）以来，图像的稀疏表示理论得到极大的发展，并取得了丰硕的成果。其基本思想是超完备字典取代传统中的正交基，字典的选择应尽可能地包含被表达图像所含有的特殊结构。其构成可以没有任何限制，字典中的元素被称为原子。

设 y∈ℝN为N维的含噪图像序列，A∈ℝM×N的过完备字典，考虑图像为加性高斯白噪声，图像稀疏表示可以用求解x的l0范数表示：

式中，ε是误差因子，x是原图像的稀疏表示。现已证明，精确求解式（1）是一个NP难题[7]。幸运的是，近些年研究人员提出了多种有效的近似求解算法，主要可以概括为贪婪追踪[6]和凸松弛[8]两类算法，常见的有MP和BP（Basis Pursuit）等。其中MP算法计算简单，并且可以获得较高的重构精度，因此在图像处理领域得到广泛应用。下面就简要描述MP算法的原理。

1.2 匹配追踪算法

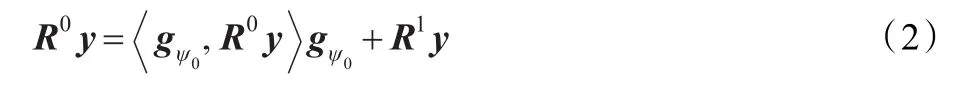
其中，gψ0为字典中使残差能量最小的原子，即展开信号与原子 gψ0的内积最大。

由于 gψ0与 R1y正交，因此满足

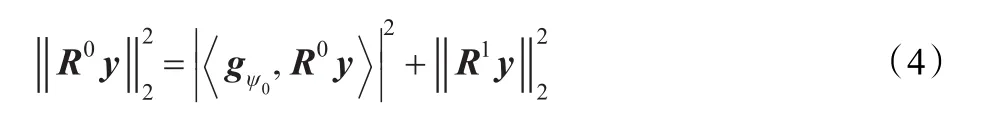
同样的方法，可以得到：

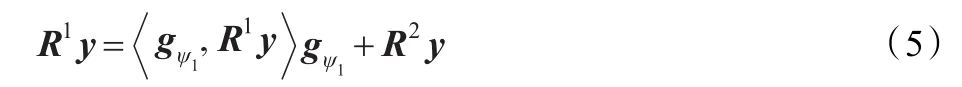
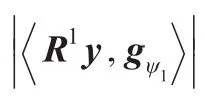
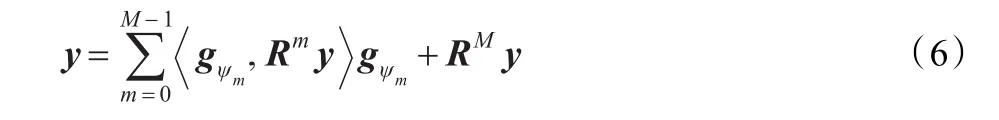
其中RMy为M项近似的残差，并且满足下式：

Mallat已对匹配追踪的收敛性进行过分析，结果表明匹配追踪时收敛的，并且在有限维条件下满足指数级收敛[6]。

2 图像稀疏收缩去噪框架

收缩是目前研究最为广泛的去噪策略，其主要思想是：图像主要由一些平滑的不重叠区域组成，这些区域是以一些边缘为界限的。因此，去噪过程中不仅要保留含有大量信息的低频分量，也要尽量保留含有边缘信息的高频分量。而收缩通过对收缩函数和阈值的选择，能够较好地保留图像的纹理和边缘信息，避免去除噪声同时造成图像的模糊。

目前，收缩主要应用于传统的正交基和紧框架。在稀疏框架下，使用超完备字典取代传统的正交基或紧框架[9]。因此，稀疏框架下收缩的过程，如图1所示。

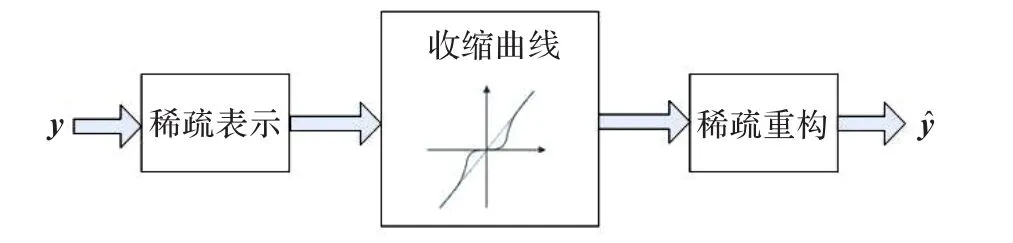
图1 稀疏框架下收缩去噪框图

设A为列l2标准化的冗余字典，为了估计式（1）的解，采用如下的收缩公式：

式中，A+表示字典 A的Moore-Penrose逆，λ表示阈值，Sλ(⋅)表示收缩函数，参量为矢量时输出结果为矢量。收缩去噪的关键在于如何选择合适的收缩函数和收缩阈值。对于收缩函数，Donoho提出了两种常用的收缩函数：硬阈值函数和软阈值函数[1]。但是这两种函数导数都不连续，而很多情况下需要对收缩函数进行一阶甚至高阶导数运算，通常采用如下高阶可导的收缩函数[11]：

其中，k表示偶常数。k取值越大，对应的曲线越接近硬阈值函数，而当k取20时，收缩曲线实际上已经非常接近硬阈值。

阈值选择问题是本文研究的一个重点，下面介绍本文提出的一种基于SURE无偏估计的自适应阈值选择算法。

3 基于SURE无偏估计的自适应阈值选择

3.1 算法的提出

图像去噪，实质上是尽可能地使图像的估计值接近本身的无噪图像。这也是图像去噪的难点，因为在实际过程中往往很难得到真实图像本身。Stein提出的Stein无偏风险估计[12]很好地解决了这个问题。SURE无偏估计推导如下：

上式是关于变量λ的隐函数，去噪的目的是使η(λ)最小化。函数 η(λ)在区间（0，+∞）是一个关于λ的凸函数，存在唯一的全局最小值。下面进行简要证明。

3.2 η(λ)关于λ的凸函数证明

由于 k 是偶常数，易知 f(λ)、g(λ)在区间（0，+∞）都是凸函数。同时根据凸函数性质易知，两个非负凸函数的正系数线性组合也是凸函数。故根据公式（18）可得，η(λ)在区间（0，+∞）是关于λ的凸函数，即 η(λ)在区间（0，+∞）存在唯一的全局最小值。由于黄金分割法仅需计算函数值，而且每次迭代只需要计算一次函数值，算法简单，适用范围广，因此可以用黄金分割法对公式（15）进行全局最小值搜索，搜索所得到的阈值即为本文的自适应阈值。

3.3 算法分析

设图像序列 y长度为N，字典 A大小为M×N，稀疏度为K。本文算法中，稀疏表示阶段采用MP算法，其算法复杂度为O(K MN )，而在迭代收缩阶段，黄金分割法每步迭代只计算一次目标函数值，在第γ步迭代中，计算一次目标函数计算复杂度为O(( k +1)MN+2(k2+3k)N ) 。设收缩阶段总迭代次数为γo，则本文算法复杂度为O(KMN+γo((k+1)MN+2(k2+3k)N))。经过大量的仿真表明，γo的数值在14左右，最大不超过20，因此本文算法的复杂度在可接受范围之内。

4 实验仿真和结果分析

为验证本文自适应阈值选择算法的有效性，对超完备字典下Visu阈值、AdpSURE阈值去噪性能进行实验对比。图像采用叠加了不同强度高斯噪声的大小为512×512的Lena、Barbara图；字典由冗余Haar小波字典构成，字典冗余度为7；收缩函数如式（9）所示，取参数k为20，采用峰值信噪比作为判定标准。

图2 两种阈值选择对应峰值信噪比曲线的位置图

图3 Lena图像去噪效果局部放大图

图4 Barbara图像去噪效果局部放大图

实验分为三个部分：（1）不同噪声强度下，Visu阈值和AdpSURE阈值去噪结果的峰值信噪比，取50组实验的平均值；（2）噪声标准差取20，分别绘出Visu阈值和AdpSURE阈值对应峰值信噪比曲线的位置图；（3）噪声标准差取20，分别用Visu阈值和AdpSURE阈值对Lena、Barbara进行收缩去噪的局部放大图。

实验结果如图2～图4所示。表1给出了不同噪声强度下两种阈值选择去噪的PSNR值，由表可知，不同噪声强度下，本文的PSNR值均高于Visu的PSNR。图2给出了两种阈值选择对应峰值信噪比曲线的位置，由图可以看出，Visu阈值存在过扼杀的现象，而本文的非常接近PSNR的极大值点。图3、图4给出了对Lena和Barbara图像的两种去噪效果的局部对比图，由图可以看出，采用Visu图片整体比较平滑，细节部分比较模糊，而本文较好地克服了这一点，无论是Lena图像中头发等边缘特征，还是Barbara图像中的纹理信息，恢复得均强于Visu阈值。

表1 不同噪声强度下两种阈值收缩去噪的PSNR dB

5 结束语

在图像稀疏收缩框架下，基于一阶可导收缩函数，提出了一种基于SURE无偏估计的自适应阈值选择算法。算法推导了基于Stein无偏估计的目标优化函数，证明了该函数是关于阈值的凸函数，用黄金分割法搜索全局最小值点，获得自适应的阈值。本文算法算法的优点体现于如下两点：（1）算法基于SURE的无偏估计，去噪过程无需真实图像本身；（2）阈值的选择接近峰值信噪比曲线的最大值点。实验结果证实了本文算法的有效性。相比于Visu阈值，本文算法无论是客观指标还是主观质量，均显示出更加优越的性能，但其仍有较大改进空间，如字典的选取等，相关工作正在研究之中。

[1]Donoho D L.De-nosing by soft-thresholding[J].IEEE Trans on Information Theory，1995，41：613-627.

[2]Donoho D L，JohnstoneIM.Idealspatialadaptation by wavelet shrinkage[J].Biometrika，1994，81：425-455.

[3]Jonstone I M，Silverman B W.Wavelet threshold estimators for data with correlated noise[J].Journal of Royal Statistical Society：Series B，1997，59（2）：319-351.

[4]Donoho D L，Johnstone I M.Adapting to unknown smoothness via wavelet shrinkage[J].Amer Stat Assoc，1995，90：1200-1224.

[5]焦李成，谭山.图像的多尺度几何分析：回顾和展望[J].电子学报，2003，31（12）：1975-1981.

[6]Mallat S，Zhang Z.Matching pursuit in a time-frequency dictionary[J].IEEE Trans on Signal Process，1993，41（12）：3397-3415.

[7]张春梅，尹忠科，肖明霞.基于冗余字典的信号超完备表示与稀疏分解[J].科技通报，2006，51（6）.

[8]Chen S S，Donoho D L，Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Rev，2001，43（1）：129-159.

[9]Elad M.Why simple shrinkage is still relevant for redundant representations[J].IEEE Transactions on Information Theory，2006，52（12）：5559-5569.

[10]曲天书，戴逸松，王树勋.基于SURE无偏估计的自适应小波阈值去噪[J].电子学报，2002，30（2）.

[11]Elad M.Sparse and redundant representations：from theory to applications in signal and image processing[M].[S.l.]：Springer，2010：298-300.

[12]Stein C M.Estimation of the mean of a multivariate normal distribution[J].Ann Stat，1981，9（6）：1135-1151.