建筑工程解析法规划验线验测点坐标归心处理方法
2013-03-03黄校程会超
黄校,程会超
(珠海市测绘院,广东珠海 519015)
建筑工程解析法规划验线验测点坐标归心处理方法
黄校∗,程会超
(珠海市测绘院,广东珠海 519015)
建筑工程解析法规划验线测量必须获取符合建筑物图形条件和特定精度要求的平面验测点坐标验测成果、获取用以评述建筑物相关空间要素与规划许可条件符合程度的平面验测点点位偏差。基于平面验测点坐标通常无法直接采集和必须通过归心处理求取的思考,本文介绍建筑工程解析法规划验线验测点坐标的归心处理方法。
规划验线;验测点;归心处理
1 前 言
规划验线是城乡规划主管部门强化和规范建筑工程批后管理、及时核查在建建筑工程的空间要素(空间位置、构造尺寸、建设形状等)是否符合规划许可要求、及时发现和纠正在建建筑工程可能发生的施工放线错误或违章建设行为的一项城乡规划监督管理工作。建筑工程解析法规划验线测量成果是城乡规划主管部门实施该项城乡规划监督管理工作的主要依据,其准确性和可靠性是影响在建建筑工程相关空间要素评定结论的重要因素之一。
建筑工程解析法规划验线测量,因受建筑物图形条件、建筑工程场地条件、或验线测量作业条件等限制,使得部分平面验测点坐标往往无法直接采集。因此,对于无法直接采集坐标的平面验测点,必须合理和精确地处理其验测数据,以获取符合建筑物图形条件和建筑工程解析法规划验线测量精度要求的平面验测点坐标验测成果、获取用以评述建筑物相关空间要素与规划许可条件符合程度的平面验测点点位偏差。
2 矩形(多边形)建筑物验测点坐标归心处理
矩形(多边形)建筑物通常选取其外围轴线的交点为平面验测点。无法直接采集平面验测点坐标者,通常采集其辅助验测点的平面坐标和归心要素、确定坐标归心计算路径,采用相应的坐标归心处理办法求解其验测坐标。
(1)辅助验测点位于两验测点连线或连线延长线上的情况:
设平面验测点A、B中的A点无法直接采集平面坐标,其辅助验测点为A-1、归心间距为d、归心计算方向角为α(投影轴设计方向角或投影轴垂直方向设计方向角),如图1、图2所示。

图1 矩形(多边形)建筑物辅助验测点布设示意图
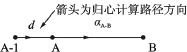
图2 矩形(多边形)建筑物辅助验测点布设示意图
①辅助验测点A-1位于A-B连线上,α为B点至A点的方向角αB-A。
②辅助验测点A-1位于A-B连线的延长线上,α为A点至B点的方向角αA-B。
依坐标归心计算路径,按式(1)求取A点的验测坐标:

(2)辅助验测点位于A-B连线或A-B连线延长线左右侧的情况:
设平面验测点A、B中的A点无法直接采集平面坐标,其辅助验测点为A-1,两个正交的归心间距为d1和d2、归心计算方向角为α1和α2,如图3所示。
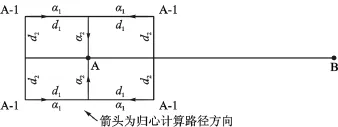
图3 矩形(多边形)建筑物辅助验测点布设示意图
依坐标归心计算路径,按式(2)求取A点的验测坐标:
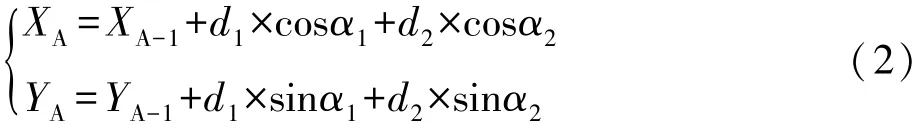
当报建批准图件无给定A点的条件坐标时,根据该矩形(多边形)建筑物条件点P的坐标(XP设、YP设)、A点许可坐标推算路径上的条件边长Si设和条件方向角αi设,按式(3)求取A点的许可坐标:

A点的点位偏差,按式(4)计算:

矩形(多边形)建筑物平面验测点坐标,可通过绘制CAD图形的方法直接归心获取。
3 圆形(圆弧形)或组合型建筑物验测点坐标归心处理
圆形建筑物通常选取其外围轴线圆周长度的四等分点为平面验测点(图5中A、B、C、D点),圆弧形建筑物或圆弧形与矩形(多边形)组合型建筑物的圆弧形建筑部位选取其外围轴线的端点和中点(图8中A、B、C点)、非圆弧形建筑部位选取其外围轴线的交点为平面验测点(图8中F点)。无法直接采集平面验测点坐标者,通常采用在现场采集其辅助验测点(测定点和检测点)的坐标、过平面三点建立验线拟合圆的圆方程、求取验线拟合圆的圆心坐标和半径、“圆-直”交会或“圆-圆”交会的方法求取其验测坐标。
(1)圆形建筑物验测点坐标归心处理
圆形建筑物验线测定点和检测点布设,如图4所示。
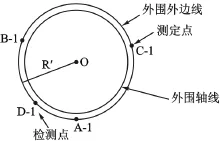
图4 圆形建筑物辅助验测点布设示意图
图4 中A-1、B-1、C-1点为圆形建筑物外围外边线上任意选取的、构成近似等边三角形的测定点,D-1点为圆形建筑物外围外边线上任意选取的检测点。
①采集A-1、B-1、C-1、D-1点的坐标,过A-1、B -1、C-1三点,按式(5)求解参考拟合圆的圆心坐标(X′O、Y′O)和参考拟合圆的半径(R′)。

建立参考拟合圆的圆方程:
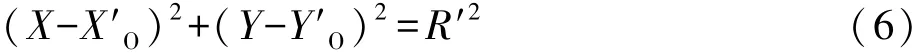
②当D-1点至参考拟合圆圆心的间距与参考拟合圆半径R′的较差不超限时(限差根据当地城乡规划主管部门制定或认可的建筑工程规划验线测量技术规定确定),顾及圆形建筑物外围外边线与外围轴线的间距d圆,建立圆形建筑物外围轴线验线拟合圆的圆方程:

式中:XO、YO为该验线拟合圆的圆心坐标(XO=X′O、YO=Y′O),R为该验线拟合圆的半径(R=R′-d圆)。
求取A-1点沿“A-1→O”方向在验线拟合圆圆周线上的投影坐标(XA、YA),以A为起点,四等分验线拟合圆圆周长度,按顺时针方向确定构成正方形的4个平面验测点A、B、C、D,如图5所示。按下式求取B、C、D点的验测坐标:
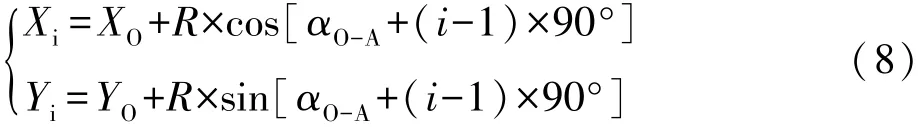
式中B、C、D点对应的i值,分别为2、3、4。
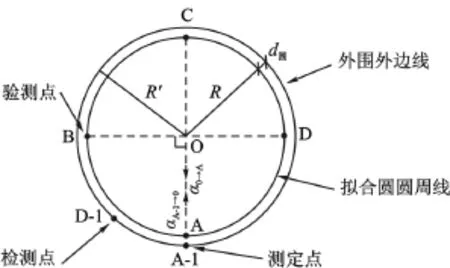
图5 圆形建筑物平面验测点分布示意图
根据报建批准图件给定的该圆形建筑物圆心点的条件坐标(XO设、YO设)和条件半径R设,按式(9)计算A、B、C、D点的许可坐标:

式中A、B、C、D点对应的i值,分别为1、2、3、4。
A、B、C、D点的点位偏差计算式同式(4)。
③当D-1点至参考拟合圆圆心的间距与参考拟合圆半径的较差超限时,则圆形建筑物的部分或全部外围外边线上的测定点和检测点的坐标测量误差超限。此时,应重新采集A-1、B-1、C-1、D-1四点的坐标,直到该较差不超限为止。
(2)圆弧形建筑物、圆弧形与矩形(多边形)组合型建筑物验测点坐标归心处理
圆弧形建筑物、圆弧形与矩形(多边形)组合型建筑物验线测定点和检测点布设,如图6所示。

图6 圆弧形、组合型建筑物辅助验测点布设示意图
图6 中A-1、B-1、C-1点为圆弧形建筑物、或圆弧形与矩形(多边形)组合型建筑物每一圆弧形建筑部位外围外边线上构成近似等腰三角形的测定点(其中A-1、C-1点为接近圆弧形建筑部位外围外边线端点的测定点,B-1点为接近圆弧形建筑部位外围外边线中点的测定点),D-1点为圆弧形建筑部位外围外边线上任意选取的检测点,E-1、F-1点(如图7所示)为与圆弧形建筑部位外围外边线相交(或相切)的非圆弧形建筑部位的任一侧外围外边线(直线)的测定点。
①采集A-1、B-1、C-1、D-1、E-1、F-1点的坐标,a.过A-1、B-1、C-1三点建立参考拟合圆的圆方程,顾及圆弧形建筑部位外围外边线与外围轴线的间距,按上述方法和要求建立圆弧形建筑部位外围轴线验线拟合圆的圆方程,并求取验线拟合圆的半径R;b.按式(2)求取E-1、F-1两点在EF投影轴的垂直投影坐标(E点:XE、YE,F点:XF、YF),如图7所示。
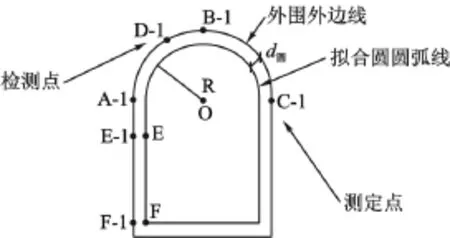
图7 圆弧形建筑部位辅助验测点布设示意图
②当圆弧形建筑部位外围轴线与非圆弧形建筑部位外围轴线(直线)相交(或相切)时(如图8所示),按下列方程求解其端点(交点或切点)A的验测坐标:
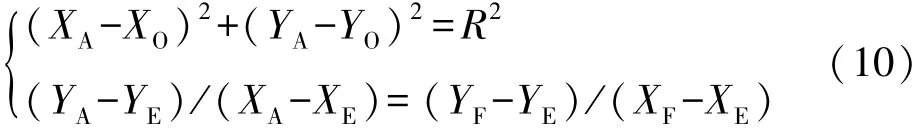
同理求解端点C的验测坐标。
③当某一圆弧形建筑部位(其验线拟合圆圆心点为O1、半径为R1)外围轴线与另一圆弧形建筑部位(其验线拟合圆圆心点为O2、半径为R2)外围轴线相交(或相切)时(如图8所示),按下列方程求解其端点(交点或切点)A的验测坐标:
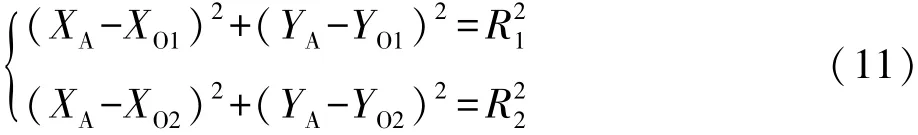
同理求解端点C的验测坐标。
④在验线拟合圆上选取与圆弧形建筑部位对应的验线拟合圆圆弧线长度,二等分该圆弧线,确定构成等腰梯形的三个平面验测点A、B、C,如图8所示。
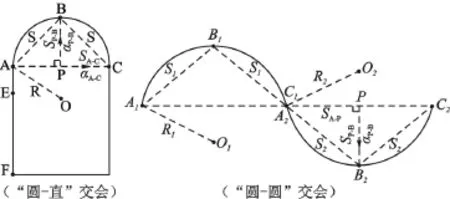
图8 圆弧形建筑部位平面验测点分布示意图
依A、C点的验测坐标和半径R,求取SA-C、SP-B、αA-C、αP-B,按式(12)求取圆弧线中点B的验测坐标:

根据报建批准图件给定的圆弧形建筑部位圆心点的条件坐标(XO设、YO设)、条件半径R设和条件圆心角β设,按式(13)计算A、B、C点的许可坐标:

式中A、B、C点对应的i值,分别为1、2、3。
A、B、C点的点位偏差计算式同式(4)。
圆形(圆弧形)或组合型建筑物平面验测点坐标,可通过绘制CAD图形的方法直接归心获取。
4 案 例
某建筑物规划验线如图9所示。

图9 建筑物规划验线略图
对无法直接采集坐标的该建筑物平面验测点进行坐标归心处理后,平面验测点成果如表1所示。

建筑物规划验线成果表 表1
5 结 语
建筑工程解析法规划验线测量是近几年随各地城乡规划主管部门强化建筑工程批后监督管理而推行的一项规划监督测量工作,其数值处理方法是亟待探索和解决的问题。笔者根据建筑物外围形状的一般建设特征和建筑工程解析法规划验线测量的特点,结合近年来对建筑工程解析法规划验线测量数值处理方法的探索结果、以及从事该项工作的经验和体会,介绍一种适用于矩形(多边形)建筑物、圆形建筑物、圆弧形建筑物、圆弧形与矩形(多边形)组合型建筑物解析法规划验线验测点坐标的归心处理方法。
[1] 中华人民共和国城乡规划法[S].2007.
[2] 国发〔2002〕13号.关于加强城乡规划监督管理的通知[R].
[3] CJJ/T 8-2011.城市测量规范[S].
[4] 黄校.基于建筑工程空间要素规划许可条件的规划验线验测点选取规则[J].城市勘测,2012(2).
[5] 董黎.房屋建筑学[M].高等教育出版社,2006.
[6] 邢双军.建筑构造[M].浙江大学出版社,2007.
The Coordinate Returning Processing method of M easuring Point for Construction Project Analytical Planning Check Line
Huang Xiao,Cheng Huichao
(Zhuhai Institute of Surveying and Mapping,Zhuhai519015,China)
Themeasurement for construction projectanalytical planning check linemustgain that coordinate resultof planemeasuring points be in keeping with building geometric condition and be in keeping with specially accuracy requirement,and must gain that position error of planemeasuring points in order to comment on conform degree that space elements related building for planning permit conditions.Based on the thinking that coordinate of planemeasuring points general unable direct gather,and must procure it pass through returning processing.this paper introduces a coordinate returning processingmethod ofmeasuring point for planning check line.
planning check line;measuring point;returning processing
1672-8262(2013)02-132-04
P258
A
2012—06—04
黄校(1959—),男,高级工程师,从事城乡规划测绘、国土与房产测量、工程测量的实践与研究。
