弯曲宽箱梁剪力滞分析

弯曲宽箱梁剪力滞分析

李成1，刘晨光2

（1中煤科工集团重庆设计研究院，重庆400016；2四川建筑职业技术学院，四川德阳618000）

该文介绍了曲线梁与直线桥区别和剪力滞效应，运用有限元软件对弯曲宽箱梁受力性能进行了分析，得出了其在自重作用下应力状态和支座处剪力滞效应规律。通过计算得出，在一定曲率半径范围内，弯曲宽箱梁在自重及偏心车道荷载作用下顺桥正剪力滞系数有较好的规律分布，最大值一般在4左右，以及外侧支座处剪力滞系数大于内侧。

弯曲宽箱梁；受力性能；剪力滞效应；应力分布；曲线梁桥；直线桥；弯扭耦合

1 概述

曲线梁桥由于结构自身存在着与直线桥最本质的区别——弯扭耦合问题[1-2]，因此曲线梁桥的设计、施工及研究的难度比直线桥大得多，并且在目前规范中关于曲线梁桥涉及的也比较少。

在宽箱梁[3]中普遍存在剪力滞后效应，忽略剪力滞效应的影响，就会低估箱梁腹板和翼板交接处的挠度和应力。如20世纪60年代国外发生的多起桥梁箱梁破坏事故。从对这些出现事故的桥梁的设计方法进行深入分析后，发现都没有仔细分析“剪力滞效应[4]”。国内桥梁设计中未考虑剪力滞效应而出现事故的桥梁也数不甚数，由于未考虑剪力滞效应，使得桥梁实际应力大于设计应力，导致应力集中造成桥梁发生破坏。

剪力滞效应的分析方法主要有五种：卡曼理论、弹性理论、比拟杆法、能量变分法、数值分析法。近年来计算机的普遍应用使得数值分析法得到了快速发展[5]，数值分析法包括有限元法、有线条法、有限段法。本文采用有限元方法进行分析，有限元分析是用较简单的问题代替复杂问题后再求解。利用有限元法分析的最大优势就是能够获取全面而又准确的应力分布图像，计算结果具有针对性和可靠性[6]。

有限元分析可分成三个阶段，前置处理、计算求解和后置处理。前置处理是建立有限元模型，完成单元网格划分；后置处理则是采集处理分析结果。

2 研究对象及模型

本文研究的弯曲宽箱梁跨径（30+36+30）m，横断面尺寸如图1所示。内侧腹板从外向内依次为1#～5#腹板，支座布置对应于2#与4#腹板位置处。混凝土密度取26kN/m3，取C50混凝土弹性模量E=3.45×104MPa，泊松比vc为0.1667。

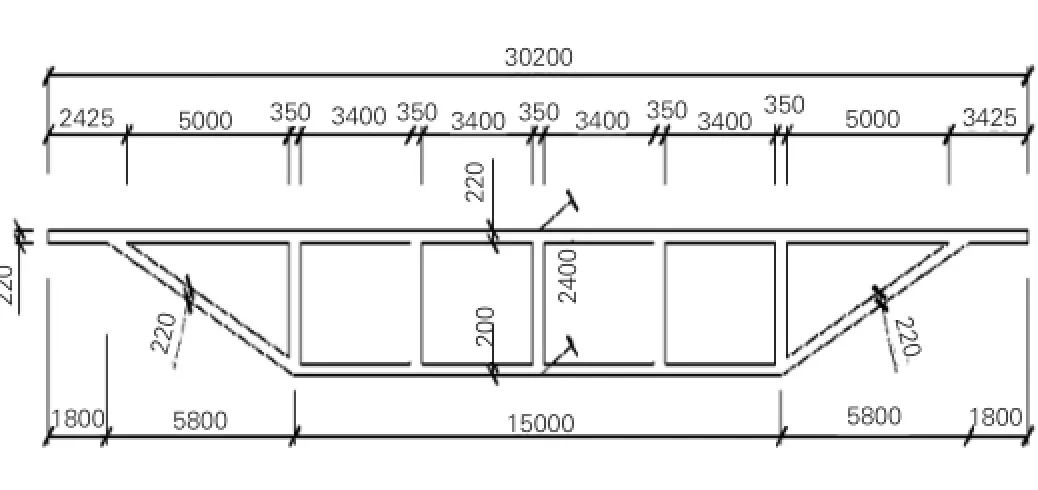
图1 横断面图

本文采用图2所示的支座布置以及图3所示的跨径布置形式，曲率半径分别选取60m、90m、120m和直桥。

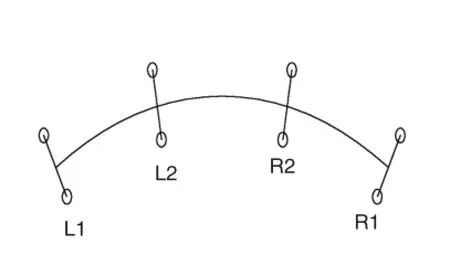
图2 支座布置图

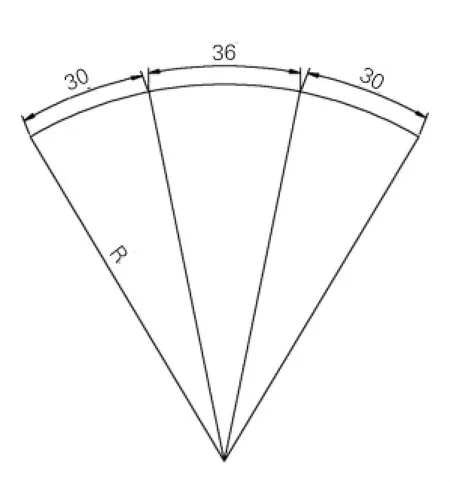
图3 跨径布置图

采用空间有限元程序ANSYS[7-8]建立简支曲线钢箱梁模型进行分析计算，箱梁顶板、底板、翼板、腹板均用板壳单元SHELL63单元模拟[9]。SHELL63既具有弯曲能力又具有膜力，可以承受平面内荷载和法向荷载。本单元每个节点具有6个自由度：沿节点坐标系X、Y、Z方向的平动和沿节点坐标系X、Y、Z轴的转动。整体坐标系为：沿桥跨方向为X方向，横桥向为Y方向，垂直桥面竖向为Z方向，原点在圆心处。

按照图1提供的板厚建立有限元模型如图4。

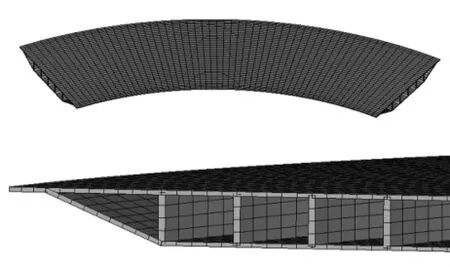
图4 有限元模型图

计算荷载考虑自重和车道荷载，其中汽车荷载全跨承受对称均布荷载，大小为q＝10.5kN/m，作用位置为翼板与腹板相交处。剪力滞系数λ[10]定义为：考虑剪力滞效应影响所求得的正应力除以按初等梁理论所求得的正应力。其中按初等梁理论所求得的正应力是根据翼板实际应力图下的面积除以翼板宽度而近似得到。

本文按照以下思路计算剪力滞系数λ：

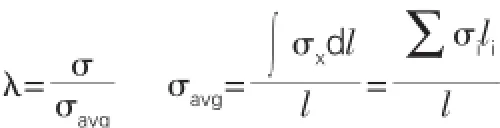
当等距离提取应力值时：

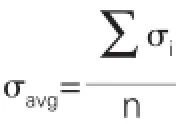
其中l为截面宽度。

3 计算结果及分析

3.1 自重作用下剪力滞效应分析

按照前述的建模参数，采用ANSYS计算结果如下，由于各曲率半径下正应力状态相似，所以图5只给出了90m自重作用下的顶板顺桥向正应力云图。

图5 自重作用下正应力云图

将不同曲率半径下L2截面桥面板正应力图提取绘制如表1和图6（表1中x为桥面到内侧边缘横桥向距离）。

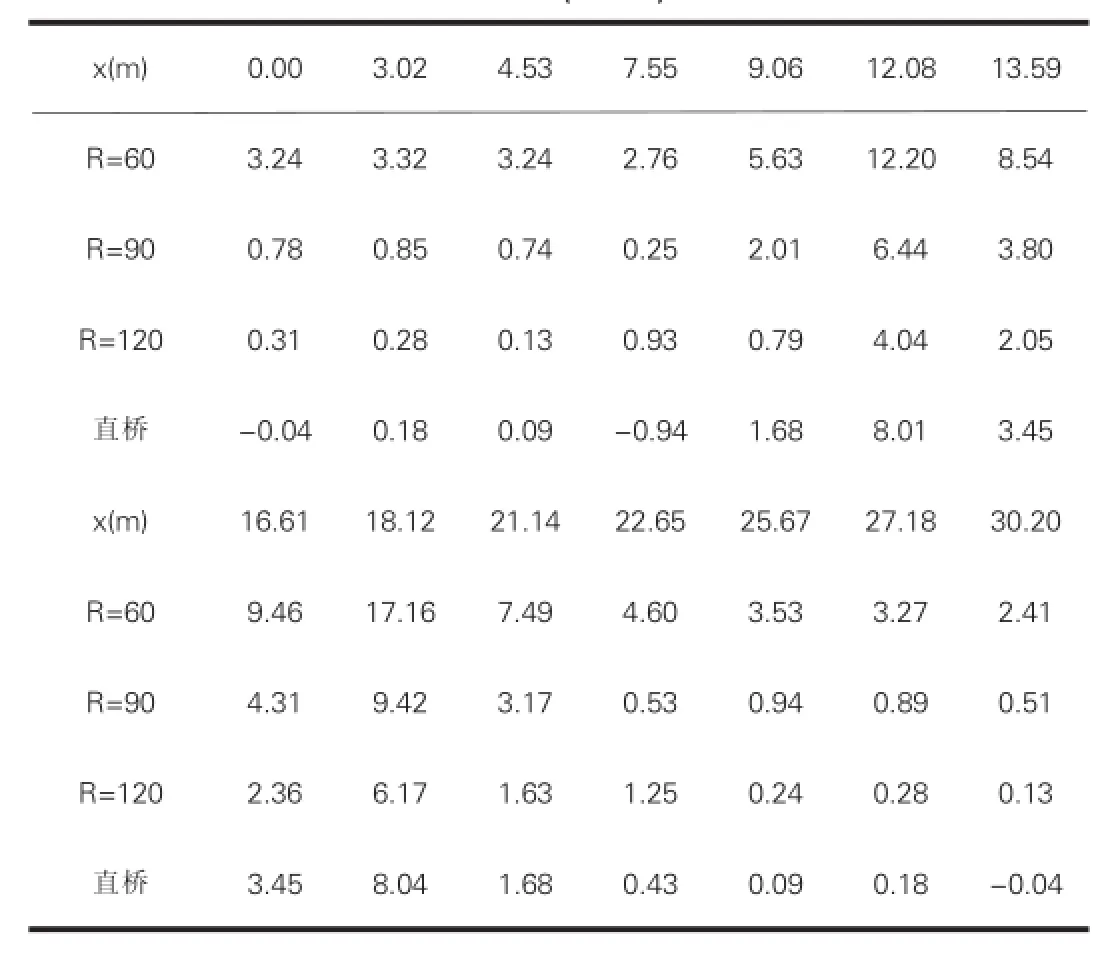
表1 自重作用下横桥向正应力值（MPa）

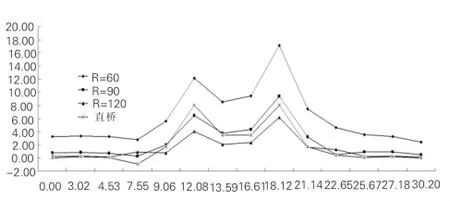
图6 自重作用下L2截面正应力分布（MPa）

从应力分布图可以看出，支座处顺桥向正应力幅随半径增大而减小，显示出很好的规律性。跨中也有相似的规律，但在直桥时有突然增大的趋势。

根据之前定义的剪力滞系数的计算方法，可计算出该截面剪力滞系数λ如表2和图7。

表2 自重作用下剪力滞效应系数

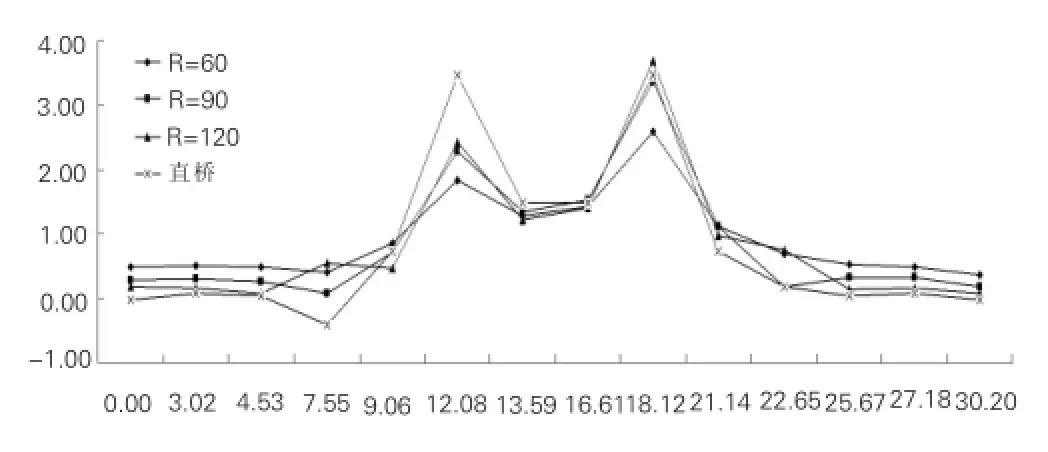
图7 自重作用下L2剪力滞系数

从表2可以看出，在自重作用下，截面外侧剪力滞系数大于内侧，其中外侧支座处剪力滞系数曲率半径为120m时达到3.69，曲率半径为120m时达到2.59，从12.08m至21.14m剪力滞系数均大于1，可见在自重作用下弯梁外侧承担大部分荷载。

3.2 偏心车道荷载作用下剪力滞效应分析

由于自重属于对称荷载，为了考虑弯梁在偏心荷载作用下受力性能。下面将车道荷载作为偏心荷载施加在弯梁上，大小根据04桥梁通用规范[11]规定的q=10.5kN/m，暂且不考虑集中荷载，位置在由外向内第二个中腹板处。计算给出80m的应力状态，结果如图8。

将L2截面正应力图提取绘制如表3和图9。

根据之前定义的剪力滞系数的计算方法，可计算出该截面剪力滞系数λ如表4和图10。

从以上计算可以看出，弯曲梁应力沿顺桥向分布呈对称形状，L2截面处顶板在偏心车道荷载作用下剪力滞系数当曲率半径在一定范围（本文中为60m～120m）时变化很相近，但在直桥状态时产生了突变，峰值由4突变到11附近，可见当曲率半径不断增大时，弯曲宽箱梁剪力滞效应越来越显著。

图8 车道荷载作用下正应力云图

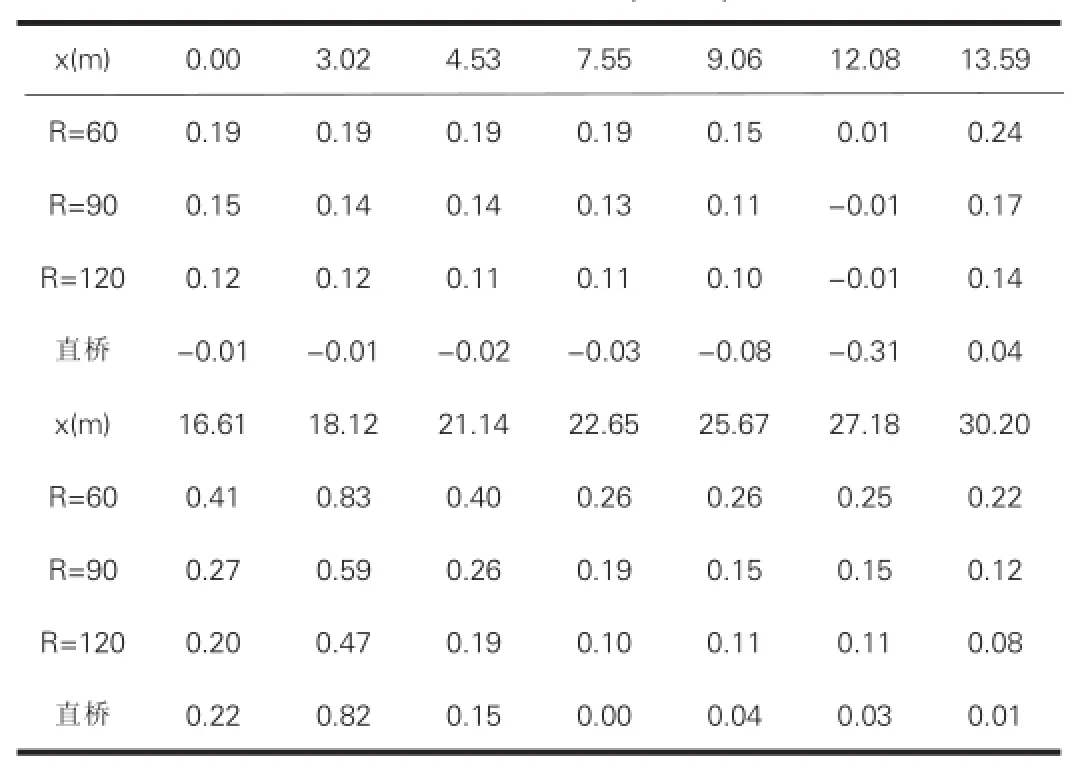
表3 车道荷载作用下横桥向正应力值（MPa）

图9 车道荷载作用下L2截面正应力分布

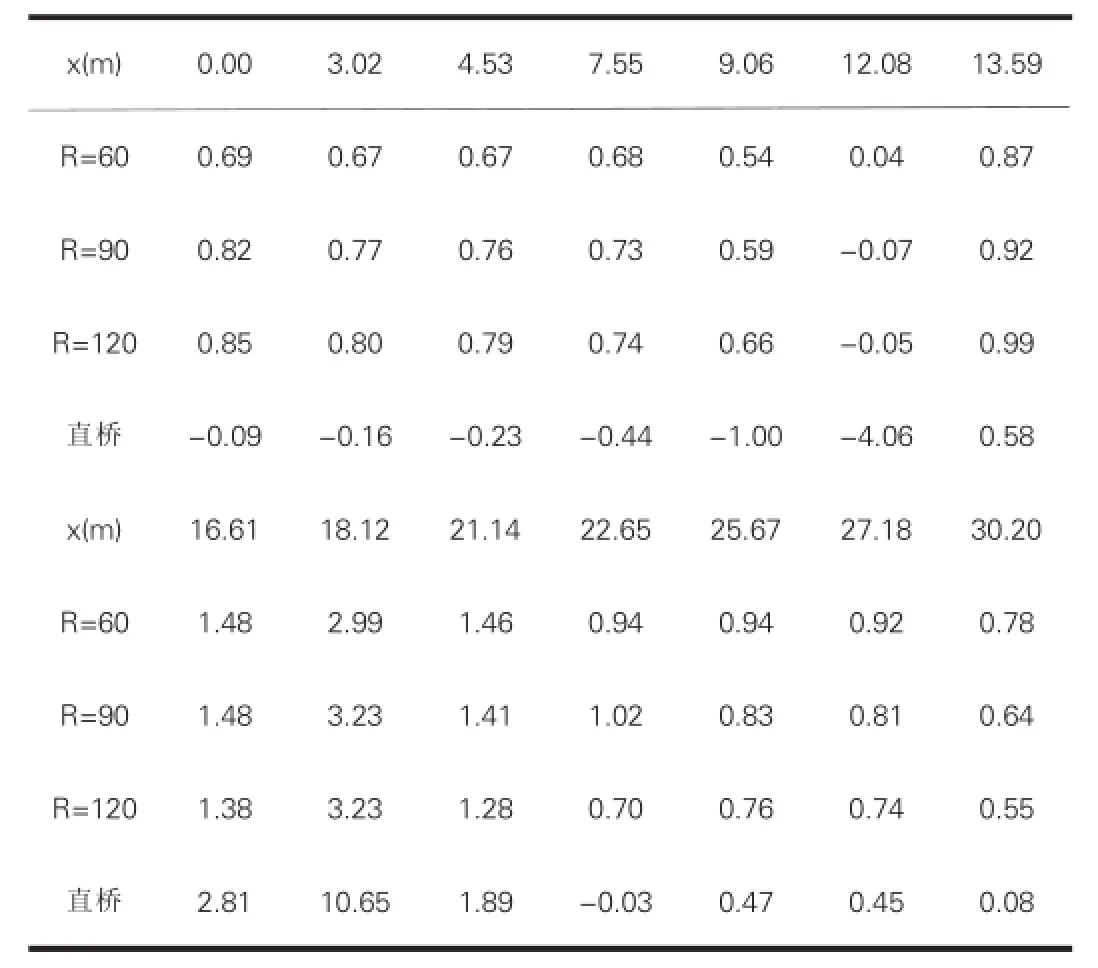
表4 车道荷载作用下L2截面剪力滞效应系数

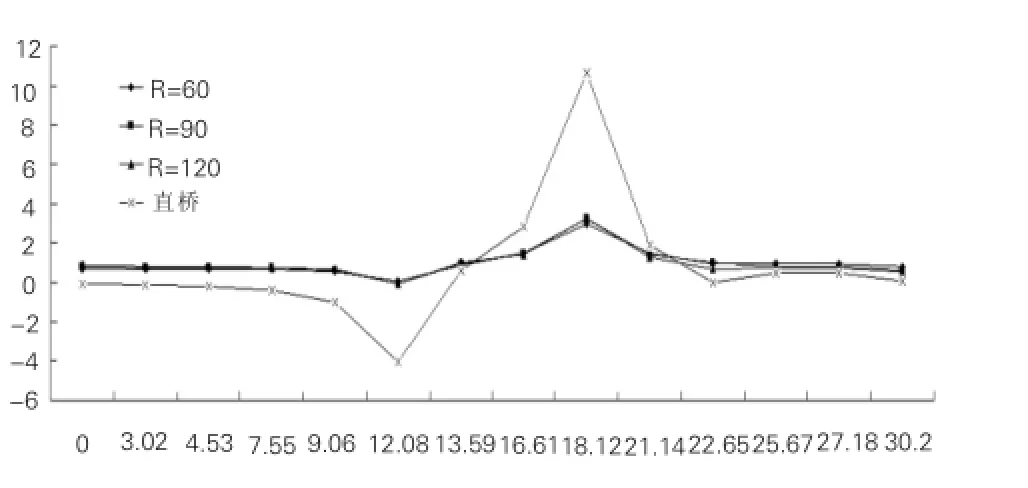
图10 车道荷载作用下L2剪力滞系数

4 结语

从本文分析可以得出以下结论。

（1）自重与车道荷载作用下，在一定的曲率半径下，弯曲宽箱梁顶板剪力滞系数一般为4，外侧支座处剪力滞系数大于内侧。

（2）自重荷载作用下，中支座处剪力滞效应呈现出良好的规律，随着半径的增大应力值减小，但在直桥时有突变。车道荷载作用下，中支座处与自重作用下有相似的规律，但剪力滞系数突变很大，峰值由4突变到11附近。

（3）本文研究了弯桥在自重与偏心车道荷载作用下的受力性能，对于不同结构体系，比如支座形式及位置改变时的受力性能有待于进一步研究。

[1]范立础.桥梁工程[M].北京：人民交通出版社，2001（7）.

[2]姚玲森.曲线桥[M].北京：人民交通出版社，1998.

[3]张士铎，邓小华，王文州.箱形薄壁梁剪力滞效应[M].北京:人民交通出版社，1998.

[4]邹毅松，李成君，易祥军.薄壁箱梁剪力滞效应计算方法研究[J].交通标准化.2012(05):93-99.

[5]周世军.箱梁的剪力滞效应分析[J].工程力学，2008，25（2）.

[6]周世军.剪力滞对箱梁弯曲刚度影响的分析[J].铁道学报，2010，32（4）.

[7]王新荣，初旭宏.ANSYS有限元基础教程[M].北京：电子工业出版社，2011.

[8]（美）莫维尼.有限元分析——ANSYS理论与应用:第三版[M].北京：电子工业出版社，2008.

[9]潘颖，邓宇.基于ANSYS平台计算分析薄壁箱梁的剪力滞效应[J].四川建筑，2007(02):153-154.

[10]杨秀珍.连续曲线钢箱梁剪力滞效应分析[J].铁道建筑，2006(2):1-3.

[11]中交公路规划设计院.JTG D60-2004公路桥涵设计通用规范[S].北京：人民交通出版社，2004.

责任编辑：孙苏，李红

清水墙保护一法

清水砖墙技术是以砖的组砌方式、拱券、挑檐、砖刻四种传统操作工艺组合而成的建筑艺术，其中以砖缝之精致为我国独有。以传统建筑砖的颜色红、灰为基调，红之温馨、灰之典雅，营造不同造型、风格的建筑，掩映在绿荫花丛自然环境中，给人以赏心悦目的感受。砖的色泽不受环境污染，是永恒不变的，砖红才是正宗的中国红，经雨水冲刷，在阳光折射下，又会呈现出一栋新楼，大雪纷飞时，又会有别样的感觉，总之清水砖墙以朴实无华的美感，使人们难以忘怀，可惜此类营造操作工艺随清水砖墙建筑日渐消失，能存留下来的更显珍贵。

在旧房改造中，对清水砖墙存在一些不好的做法，望能引以为戒。

(1)用颜色涂料。美容"清水墙，用画笔描绘砖缝，且不说涂料与砖面粘结能否持久，这种做法使原来清晰整洁的墙面变得模糊，犹如舞台布景。

(2)用面砖覆盖清水墙。上海优秀建筑延安中路四明村、虹口海沦路名人街都是这样做的，这好比在给历史建筑戴假面具，不可思议。

(3)在各种墙体基面上通贴面砖是当今的时尚装饰，这种做法不考虑建筑结构的具体部位，方式混乱，清水砖墙组砌方式有严谨的规则，要依据建筑结构部位不同，采用不同方式。

(4)在清水墙面上抹水泥砂浆涂红粉，划缝做假清水墙。

(5)用酸洗清水砖墙面上的老年斑，恢复建筑青春，这相当于当今"美容增白"，是在破坏墙面的颜容。清水砖墙建筑故旧沧桑、砖面变旧以及斑痕缺损正是建筑珍贵的历史遗痕，是城市记忆的标志，作为旧房改造管理者要了解历史，尊重先辈工匠的劳动成果，保护建筑原有历史风貌，是大家共同的责任和义务。

（摘自：《建筑工人》）

Analysis on Shear Lag of Curved Wide Box Girder

Differences between curved beam and straight bridge and the shear lag effect are introduced.The finite element software is adopted to analyze the mechanical behavior of curved wide box girder,and the stress distribution and the shear lag effect rules under self-weight are obtained.Through calculation,in a certain curvature radius,the shear lag effect of curved wide box girder under self weight and eccentric lane load is regularly distributed,its maximal value is generally 4,and the shear lag coefficient at outer support is larger than that at inner support.

curved wide box girder;mechanical behavior;shear lag effect;stress distribution;curved beam bridge;straight bridge;bending-torsional coupling

U448.21+3；TU31

A

1671-9107（2013）09-0041-04

10.3969／j.issn.1671-9107.2013.09.041

2013-07-21

李成(1982-)，男，青海门源人，研究生，助理工程师，主要从事结构、岩土设计方面的工作。