小世界网络下电网连锁故障预测

潘一飞，李华强，贺含峰，王伊渺，廖苑晰，李 扬

（1.四川大学电气信息学院，智能电网四川省重点实验室，成都610065；2.四川省电力公司科技信通部，成都610041）

近年来，随着电网规模的日益扩大，电网的安全性、可靠性等问题也越来越受到关注。电网发生大规模停电的可能性也显著增大，连锁故障被认为是引发这些灾难性事故的主要原因[1-2]。研究连锁故障的发生、发展，合理分析连锁故障的初始扰动和后续发展关系，已成为研究的热点。

从目前所研究连锁故障的成果来看，基于小世界网络模型的研究一般都是将电网考虑为无向无权网络。文献[3-9]分别对中美、北美等典型电网的拓扑结构进行比较，并分析了小世界网络特性对连锁故障传播的影响和解决方法等，但都存在着各自优势和不足。

本文结合小世界网络特性和电网运行状态，提出一种新的连锁故障预测方法。首先由小世界网络特性确定电网内支路发生故障的优先级，综合考虑支路的物理特性、电气参数、有功和无功特性来修正复杂网络理论衍生出的介数，并建立基于支路静态能量函数模型的能反映线路潮流变化、电压变化、发电机出力变化及负荷变化等的综合裕度指标。最后，给出基于小世界网络结构和电网状态的连锁故障预测方法，并通过对IEEE-57母线系统仿真，验证了该方法的可行性和有效性。

1 小世界网络模型的连锁故障的传播机理

1.1 小世界网络的模型

小世界网络是一种介于规则网络和随机网络之间的网络。对规则网络中的每一个节点，以概率p 断开与其连接的边，并从网络中的其他节点随机选择进行重新连接，则形成小世界网络[10]。文献[11]通过网络连线的随机重连建立了小世界网络的模型。小世界网络兼具了较大的聚类系数C 和较小的平均距离L，其拓扑特征表现为

式中：CRAMDOM和LRAMDOM分别指与小世界网络具有相同节点数和相同平均度数的随机网络的聚类系数和平均距离。

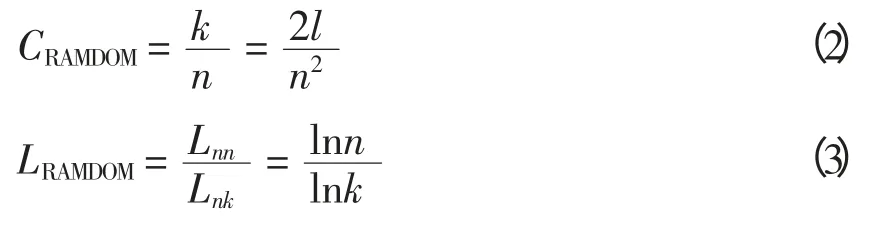
式中：n 为网络的节点数；k 为每个节点的平均度数；l 为边数。聚类系数C 和平均距离L 是复杂网络理论中衡量网络拓扑结构特征的两个重要指标[12]，即

式（4）中聚类系数C 为网络中所有节点的聚类系数的平均值；式（5）中平均距离L 为任意两节点之间距离的平均长度。它们分别反映了网络的紧密程度和网络中任意两点间平均距离，聚类系数和平均距离分别对应着故障传播的广度和深度。

1.2 电网连锁故障在小世界网络中传播机理

文献[13-14]通过对中、美两国的两个大区域电网的拓扑统计特性（平均距离、聚类系数、节点度数分布和最短路长度分布等）进行对比分析，证明两网络都属于小世界网络。在此基础上，定性分析指出小世界网络中故障传播的速度和影响范围远大于相应的规则网络和随机网络。

2011年我国某区域实际电网拓扑参数如表1，此区域电网建模时只考虑了220 kV 及以上线路，对配电网络、发电厂和变电站的主接线结构忽略不计，输电线、变压器支路是电网拓扑模型中的边，合并同杆并架的输电线，不计并联电容支路，即消除电网拓扑模型中的自环和多重边，使相应的图成为简单图。此电网的无权拓扑网络对应表1中的无权模型，而表1 中电网（220 kV 以上）与小世界网络中具有相同节点数和相同平均度数的随机网络的聚类系数CRANDOM和平均距离LRANDOM。将表1 数据与式（1）比较分析，发现该电网在无权模型中，网络具有小世界网络特性。由于该电网水电资源丰富，水电厂占总发电量比例较高，表1 中丰水期和枯水期数据是考虑水电厂因季节性变化而造成发电机出力不同的影响且对拓扑网络进行加权后的数据，可发现该电网的加权拓扑网络仍具有小世界网络特性。因此该电网具备较高聚类系数和较小平均距离的特性。小世界网络兼具宽的广度和大的深度，意味着故障影响范围和传播速度高于相应的规则网络和随机网络。

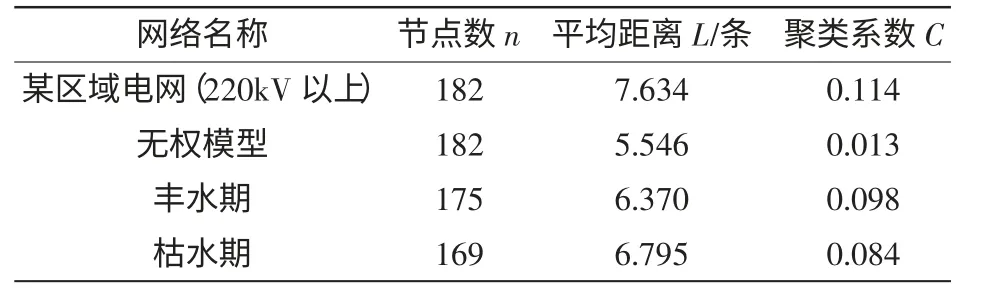
表1 2011年我国某区域实际电网拓扑参数Tab.1 Topology parameters of the regional real power grid in 2011

文献[15]提出长程连接概念。在此区域实际电网中，度数较大的联络节点占总节点的比率较小，而担负的输电任务远高于其他节点，它们是跨区域联络线两端的节点，即长程连接的两端节点。在电网中长程连线一般多为500 kV 及以上超高压线路，这些线路一般情况下较稳定，基本不会出现过负荷。然而，一旦与这些线路相关节点发生故障而导致线路退出运行，过负荷形式会通过长程连接快速传播，导致其他相关线路相继跳闸，电网失负荷值迅速增加，进而导致整个系统崩溃、解列和灾变。所以这些长程连接在保障电力运输和传送的同时，也会增加电网安全运行的风险。

2 连锁故障指标构建

2.1 支路静态能量函数模型

文献[16]建立了节点能量函数模型，本文根据支路传输的有功功率与无功功率建立相应的支路静态能量函数模型，表征支路潮流的变化在能量积累上的映射。

基于图1 所示支路模型，根据支路功率传输关系，支路ij 的潮流表达式可表示为

式中：Pij、Qij分别为支路ij 当前传输的有功功率和无功功率；Bij是支路ij 的电纳；Gij是支路ij 的电导。支路能量是由支路传输的有功功率和无功功率对应的能量两部分组成。支路传输的有功功率主要由支路两节点间的电压相角差决定，而无功功率主要由支路两节点间的电压幅值差决定。因此，完整的支路能量函数应对电压相角差和电压幅值差两部分同时进行积分[16]，表达式为

2.2 小世界网络的连锁故障的搜索优先级

文献[17]基于网络拓扑及图论，通过以各节点的负荷大小或节点介数衡量该节点的重要程度，结果显示超过2%的高负荷节点的退出会引发系统连锁故障并造成系统崩溃。通过基于小世界网络模型的电网连锁故障传播机理分析和对支路发生故障可能性的排序，本文对具有较大故障可能性的支路给予优先搜索和较大的权重系数。从而避免了搜索的盲目性，提高了搜索效率。搜索优先级排序一般有以下规律。

1）重要发电机、负荷和长程连接支路对故障传播起重要作用，因此这些支路优先级最高。

2）越靠近故障点的支路的潮流变化越明显，因此在故障点附近的支路也有较高的优先级。

3）大多数电网发生连锁故障的原因主要是由于继电保护装置的误动和拒动，这也是造成连锁故障蔓延的主要原因[19]，将包含这些装置的支路作为搜索的第三优先级。

基于小世界网络特性研究连锁故障时，优先级较高的线路通常是最容易出现故障的支路。在分析连锁故障时首先对这些故障优先级较高的支路进行评估和分析，能够提高搜索效率，减少计算时间。

2.3 基于小世界网络模型的有向加权拓扑建模

由于电网自身物理特性与运行特性，使得直接应用小世界网络理论解析电网实际问题存在不足，从而需对电网初始网络拓扑进行改造，本文结合近年来研究成果，提出有向加权介数的方法。

由于电网有功网络与无功网络存在着一定的联系，通过分析可以发现：有功功率一般由发电机节点到负荷节点，则由此可认为电网中最短的有功电气路径为由有功注入的节点指向有功汲取节点；无功电气路径为由无功注入的节点指向无功汲取节点。定义有向加权最短电气路径表达式为

式中：Zij为线路ij 的阻抗；V0表示线路的基准电压等级；vij为线路ij 的电压。在线路ij 中电压落差相同，阻抗越小，线路传输的电能就越多，权重值就越小。而对于线路损耗来讲，本文通过增加虚拟节点R 的方法对网络进行无损化处理。在电网中，一般在有功网络增加有功汲取（负荷）节点，在无功网络根据无功正方向的选取，增加无功汲取节点或无功注入节点。此虚拟节点R 所在的线路被分成两段，每段线路阻抗为原线路的一半，即

经以上处理，将一个无权无向的电网拓扑网络模型转化成两个（有功网络和无功网络）有权有向的拓扑网络模型。在小世界网络模型中，一般采用图论概念中潮流沿最短路径传播的概念，大多未结合电力系统的物理特征，使传统介数存在局限性。本文采用加权介数不仅反映了线路被最短路径经过的次数，也反映“发电–负荷”节点对之间潮流对线路的利用情况，量化了支路对全网潮流传播的贡献，同样可用于系统关键线路的识别，结合式（9）～式（11）并增加虚拟节点R 后，提出了在有向加权拓扑模型下利用小世界网络结合电网运行状态的方法，得到线路ij 的加权评估指标Mij，即

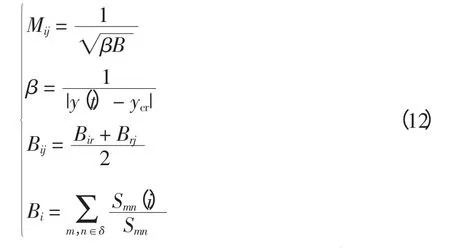
式中：B 为电气介数；β 为可能引起连锁故障的线路危险度（脆弱性）；y（t）为某时刻系统的运行状态；ycr为临界值；Smn（i）为m，n 之间的最短电气路径中经过节点i 的条数。如表2 为IEEE-14 节点母线系统加权拓扑模型（包括有功模型和无功模型）的加权电气介数B 和加权平均指标Mij。

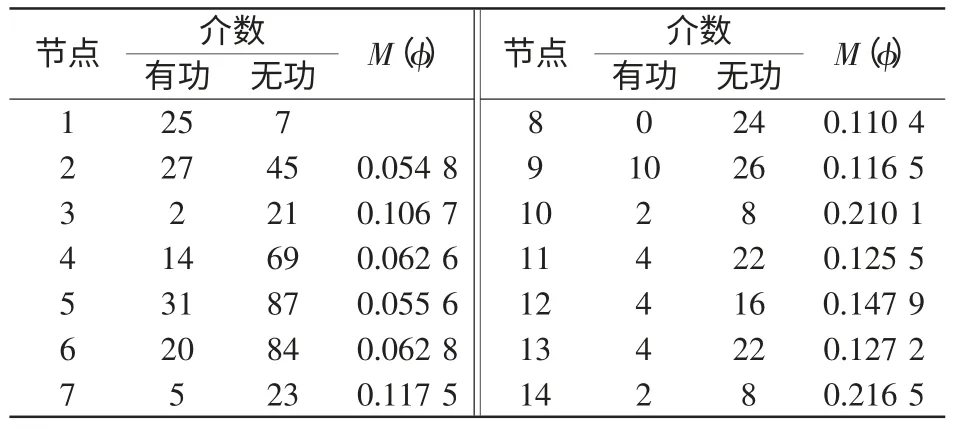
表2 IEEE14 节点系统拓扑加权拓扑模型（有功和无功模型）的介数和加权平均指标Tab.2 Referral number and weighted average index of weighted topology model（active and reactive model）of IEEE 14 node system topology

3 连锁模式预测的综合裕度指标介绍

若以某一级故障后系统仍能保持静态稳定的新拓扑结构为例，对支路ij 来说有一个初始稳定运行点δijs和Uijs，按照一定的负荷增长方式增加负荷，求得支路ij 在系统负荷增长最大承受能力下的临界运行点δijc，Uijc，即可得如式（8）所示的支路ij在该级故障后由稳态到临界状态积累的静态能量。Eij（s）表征系统s 级故障后的能量裕度，即系统正常运行与故障运行的能量差值，其值越大，表征移除该线路对系统影响越大。则支路在当前状态下越脆弱，越容易成为下一级故障。将式（12）中的线路加权评估指标作为结构因子，加权于线路的静态能量，综合得出基于小世界网络模型结构和电网运行状态的评价指标为

式中：线路ij 的加权评估指标Mij反映支路ij 在网络结构中的活跃程度，对线路的状态脆弱强度进行有效放大。εijs综合反映了线路在系统当前运行状态下的结构和状态脆弱性，其考虑了不同传输线的物理特性、电气参数以及实际电网中存在的功率损耗、有功功率和无功功率等因素，更真实地反映出电网处于小世界网络模型时实际的运行状态和线路的结构特征。计及前一故障级的累积效应，系统发生第s 级故障后，第s+1 级故障线路可以通过预测得，即

式中：线路ij 的加权评估指标Mij综合反映支路ij在网络结构的活跃程度，其综合考虑不同传输线的物理构造特性和电气参数存在的差异，实际电网中存在着阻抗、功率损耗和有功功率、区域解耦特性的无功功率。这就能够真实地反映出电网处于小世界网络模型时实际的运行状态和线路的结构特征，并能够运用Mij反映电网此时的危险度。若Mij越大，则表示此支路越危险，越脆弱，更容易成为连锁故障的下一极。将Mij加权于Eij（s）得到的综合评判指标εij（s），此值就是将基于小世界网络模型的电网结构与基于电网状态的潮流综合，其能够对状态脆弱强度进行有效放大。该指标可综合反映线路在系统中结构和状态特征。Cij（s+1）表示系统发生了s 级故障，分别反映系统的历史、当前和临界运行状态及电网结构的综合性裕度指标。其首项为支路ij 在s 级故障后的综合指标，第二项则为s 级故障后在第s-1 级故障的基础上综合指标的变化率，第三项表示第s 级故障在第s-2 级故障的基础上综合指标的变化率。该指标预测出来的连锁模式为系统较严重的故障模式。利用上述算法进行连锁故障预测，算法流程如图2 所示。

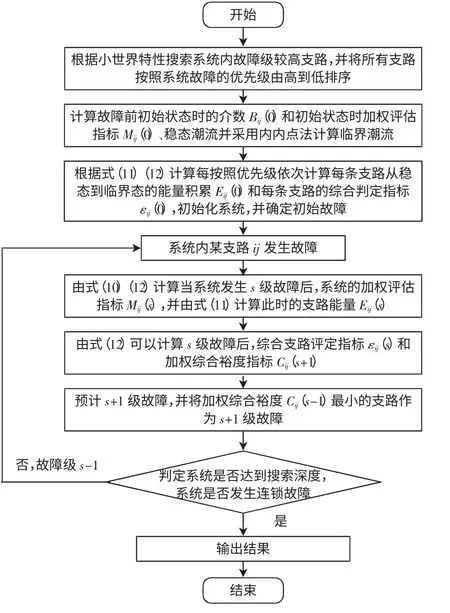
图2 小世界网络下电网连锁故障预测流程Fig.2 Flow chart for cascading failure prediction of power grid in the small world model

4 算例分析

通过IEEE-57 节点母线系统来验证本文方法的性能。首先进行故障优先级的搜索，如图3 中，横坐标表示IEEE-57 节点中的支路序号，纵坐标表示电网处于正常运行状态时各支路发生故障的优先级指标，其值越大，则支路发生故障的优先级越高，该支路发生故障的可能性就越大。

图3 IEEE-57 节点母线系统正常运行时支路故障优先级Fig.3 Slip fault priority at normal running of IEEE-57 node bus system

由图3 可知序号为20、59、60、27 和25 的支路的故障优先级指标较高，则以上支路发生故障的可能性较大。现在分别以上述支路故障作为初始故障，得到后续故障的线路序列如表3 所示。

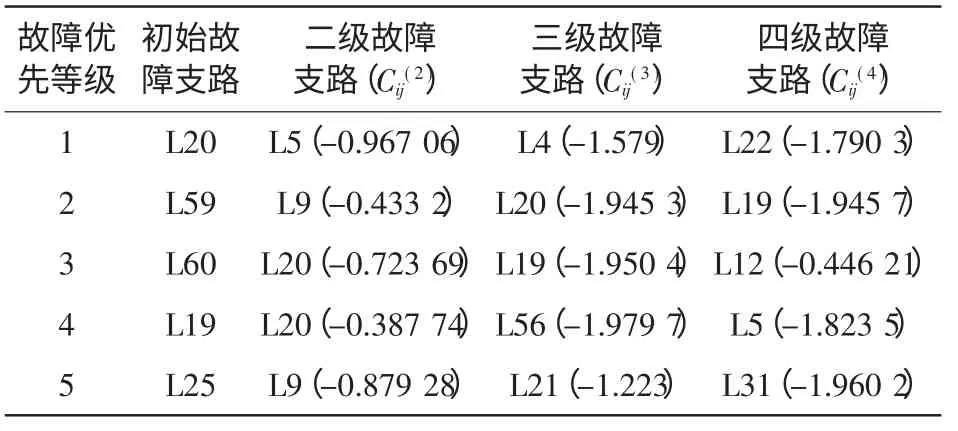
表3 故障优先级支路发生故障后续预测线路及其指标Tab.3 Follow-up predicted line and its index after the fault in slip fault priority

由表3 中可以发现在表3 中优先级较高支路易发生故障，成为故障发生支路，从而推动连锁故障发展。这些支路发生故障的原因很多，但大部分是因为支路距离初始故障较近，发生故障后潮流大量转移到线路上，极大地提高了潮流值，同时也减少了与临界态的距离；也有是因为距离发电机、负荷和长程连接较近；也有一些线路是因为要考虑故障后系统从稳定运行状态到临界运行状态对支路功率的积分。这些都与本文前面所述相吻合。同时不能排除的还有以下两个原因：故障后潮流转移引起剩余线路的过负荷或者由于隐性故障，即某条线路断开后，与其相邻的线路继电保护误动作；潮流转移只是一个表面的原因，真正的原因是故障引起的新的稳态潮流到临界潮流距离的变化，这也说明仅考虑潮流变化率来预测后续故障的可能也存在一定的局限性。基于小世界网络结构和电网状态的连锁故障的预测方法可以快速、有效地搜索到连锁故障的蔓延过程，及时采取校正措施。所提模型克服了已有的预测连锁故障模型中仅考虑潮流或结构一方面的不足，能较正确地评价不同节点在电网潮流传播中的作用以及不同初始节点故障类型对系统连锁故障过程的影响，物理背景更符合电力系统实际。

5 结语

本文以小世界网络特性为基础，综合支路静态能量函数模型，构建了综合考虑支路物理特性、网络结构参数和状态参数的综合加权裕度指标对后续故障进行预测。建立在小世界网络模型基础上的预测指标利用了快速搜索优先级的概念，结合了电网的实际运行情况，物理意义清晰，有较快的速度。通过对系统发生连锁故障的分析，可以有效地判断哪些支路、节点容易发生故障和连锁故障过程中的规律性结论，这对于由连锁故障引起的大停电事故的预防有一定的指导意义。

[1]王英英，罗毅，涂光瑜，等（Wang Yingying，Luo Yi，Tu Guangyu，et al）.电力系统连锁故障的关联模型（Correlation model of cascading failures in power system）[J].电工技术学报（Transactions of China Electrotechnical Society），2012，27（2）：204-209.

[2]宋毅，王成山（Song Yi，Wang Chengshan）.一种电力系统连锁故障的概率风险评估方法（A probabilistic risk assessment method for cascading failure of power system）[J]. 中国电机工程学报（Proceedings of the CSEE），2009，29（4）：27-33.

[3]孟仲伟，鲁宗相，宋靖雁（Meng Zhongwei，Lu Zongxiang，Song Jingyan）. 中美电网的小世界拓扑模型比较分析（Comparison analysis of the small-world topological model of Chinese and American power grids）[J]. 电力系统自动化（Automation of Electric Power Systems），2004，28（15）：21-24，29.

[4]曹一家，刘美君，丁理杰，等（Cao Yijia，Liu Meijun，Ding Lijie，et al）.大电网安全性评估的系统复杂性理论研究（Research on system complexity theory for security evaluation of large power grids）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2007，19（1）：1-8.

[5]方勇杰（Fang Yongjie）. 美国“9·8”大停电对连锁故障防控技术的启示 （Lessons from September 8，2011 southwest America blackout for prevention and control of cascading outages）[J]. 电力系统自动化（Automation of Electric Power Systems），2012，36（15）：1-7.

[6]Kinney R，Crucitti P，Albert R，et al. Modeling cascading failures in the North American power grid[J].European Physical Journal B，2005，46（1）：101-107.

[7]卢锦玲，陈媛，朱永利（Lu Jinling，Chen Yuan，Zhu Yongli）. 基于输电线路过负荷特性的连锁事件识别（Identification of cascading failures based on overload character of transmission lines）[J]. 华北电力大学学报（Journal of North China Electric Power University），2007，34（5）：27-31.

[8]徐林，王秀丽，王锡凡（Xu Lin，Wang Xiuli，Wang Xifan）.基于电气介数的电网连锁故障传播机制与积极防御（Cascading failure mechanism in power grid based on electric betweenness and active defense）[J]. 中国电机工程学报（Proceedings of the CSEE），2010，30（13）：61-68.

[9]管霖，郑传材（Guan Lin，Zheng Chuancai）.线路N-K 停运机理及其概率模型（Transmission line N-K outage mechanism and its probability model）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（4）：115-119.

[10]曾宪钊.网络科学[M].北京：军事科学出版社，2006.

[11]Watts D J，Strongatz S H. Collective dynamics of `smallworld'networks[J].Nature，1998，393（6684）：440-442.

[12]杨蕾，黄小庆，曹丽华，等（Yang Lei，Huang Xiaoqing，Cao Lihua，et al）.考虑区域性的复杂电力网络演化模型（Novel evolving network model for complex power grid considering regionality）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（2）：5-11.

[13]孟仲伟，鲁宗相，宋靖雁（Meng Zhongwei，Lu Zongxiang，Song Jingyan）.中美电网的小世界拓扑模型比较分析（Comparison analysis of the small-world topological model of Chinese and American power grids）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（15）：21-29.

[14]郑阳，刘文颖，温志伟（Zheng Yang，Liu Wenying，Wen Zhiwei）.基于小世界网络的电网连锁故障实时搜索系统（A real-time searching system for cascading failures of power grids based on small-world network）[J]. 电网技术（Power System Technology），2010，34（7）：58-63.

[15]邓慧琼，艾欣，余洋洋，等（Deng Huiqiong，Ai Xin，Yu Yangyang，et al）.电网连锁故障的概率分析模型及风险评估（Probability analysis model and risk assessment of power system cascading failure）[J].电网技术（Power System Technology），2008，32（15）：41-46.

[16]刘慧，李华强，郑武，等（Liu Hui，Li Huaqiang，Zheng Wu，et al）.基于电压脆弱性的支路事故排序快速算法（Fast algorithm of branch contingency ranking based on voltage vulnerability）[J]. 电力系统保护与控制（Power System Protection and Control），2010，38（23）：177-181.

[17]刘群英，刘俊勇，刘起方（Liu Qunying，Liu Junyong，Liu Qifang）. 基于支路势能信息的电网脆弱性评估（Power grid vulnerability assessment based on branch potential energy information）[J]. 电力系统自动化（Automation of Electric Power Systems），2008，32（10）：6-11.

[18]Albert R，Jeong H，Barabasi A. Error and attack tolerance of complex networks[J]. Nature，2000，406（6794）：378-382.