TVD格式在上游调压室水击数值模拟中的应用
2013-02-26黄逸军刘韩生
黄逸军,刘韩生
(西北农林科技大学水利与建筑工程学院,陕西杨凌 712100)
TVD格式在上游调压室水击数值模拟中的应用
黄逸军,刘韩生
(西北农林科技大学水利与建筑工程学院,陕西杨凌 712100)
为了模拟含上游调压室水电站的水力过渡过程,采用TVD格式求解水击方程,并结合调压室系统的基本方程组和给定的边界条件来模拟水击压力变化。将此方法用于工程实例,其计算所得的水头与实测水头相吻合;并将计算所得的水头与MacCormark格式和Lax-Friedrichs格式的计算结果比较,结果表明:TVD格式能有效模拟含上游调压室的水击现象,其结果具有耗散性低,不产生虚假数值震荡,计算精度高等优点。
水击数值模拟;TVD格式;水力学;调压室
压力水管中因水体流速瞬时变化(如突然关闭或打开阀门)引起管内水体压力波动,产生很大的撞击力,这种瞬时压力波动现象称为水击,调压室普遍应用于水电站中就是用以减小水击压强的。水电站阀门的开闭往往引起下游压力管道、上游引水隧洞以及调压室等中水体的非恒定流动。压力管道内的水击方程属于拟线性双曲型偏微分方程,TVD格式是一种高分辨率差分格式,能够很好地求解水击方程。现采用TVD格式求解水击方程,再结合调压室基本方程组计算,这样就能较为完整地模拟上游调压室系统的水力过渡过程。
1 二阶TVD格式
在众多的水击计算数值解法中,TVD格式是较为成功的方法。定义函数u的总变差为:TV(un)=,如果某种差分格式满足TV(un+1)≤TV (un),则称之为TVD格式。TVD格式在间断附近不会产生虚假数值震荡,且对间断有高分辨率。因为TVD格式属于激光捕捉法,故而需要有统一的守恒格式。以往的研究对TVD格式做了详细的介绍,并且将水击控制方程推导出适用于TVD格式的严格守恒形式[1]。本文在此基础上,进一步将TVD格式求解水击方程应用于上游带调压室的电站水击计算中。
考虑标量形式的双曲型守恒律方程,TVD的具体形式为[2]

式中f为物理通量。式(1)的一般显式格式可写成
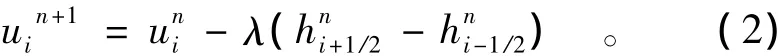
式中,时空步长比λ=Δt/Δx;数值通量h的形式为
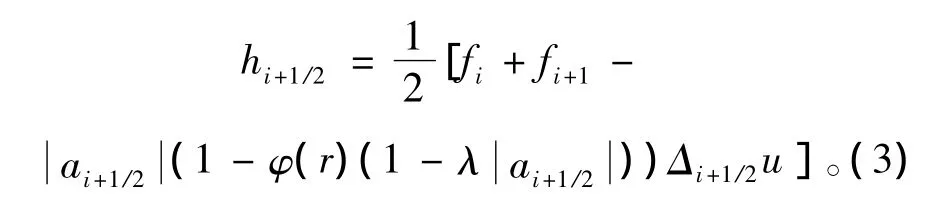
式中:r=Δi+1/2-σu/Δi+1/2u,Δi+1/2u=ui+1-ui,σ=sgn (ai+1/2);φ(r)为通量限制函数。
本文选用Roe的Superbee型限量函数:φ(r)= max[0,min(2r,1),min(r,2)]进行计算。
2 水击方程的二阶TVD格式
水击控制方程是一组拟线性双曲型方程组:

式中:H为测压管水头;v为断面平均流速;θ为管道倾斜度;J=λv2/2D,其中λ为沿程水头损失系数,D为管道直径;c为水击波波速。
将水击控制方程转化为严格守恒形式[3]:


上述标量方程的TVD格式是在标量常系数方程上定义的,而要将此格式运用到方程组式(6)上,就要经过特征理论解耦[4],即对方程组的系数加以局部冻结,然后应用单一方程的TVD格式进行推广。
现假设Y=R-1U,则式(6)解耦为

用αl取代式(3)中的r的表达式中的u,即得式(13)中r的表达式。现在将式(7)至式(10)以及式(6)中的U,S和F的表达式代入式(11),式(12)以及式(13)中就得到了水击方程的二阶TVD显式格式,再结合一定的边界条件和初始条件就可以进行求解。
3 边界条件
3.1 上游调压室边界条件
压力管道上游为调压室系统。调压室系统的基本方程为[5]

式中:z为调压室水面相对基准面的高度,规定向上为正;AT,AS分别为上游引水隧洞的横断面积和调压室的横断面积;Q为水轮机的引用流量;L为上游引水隧洞的长度;v为上游引水隧洞的水流流速;ζc为上游引水隧洞的水头损失系数;hf为阻抗孔处的水头损失。
对于式(14)和式(15)可以采用四阶龙格库塔法进行求解。
3.2 下游边界条件
给定下游的边界条件为[6]

式中:vm为阀门全开时的管中流速;H0为恒定流时管道末端的作用水头;τj为j时刻管道末端的阀门相对开度。根据特征线理论,沿着C+特征线有

4 初始条件
初始条件是指水击现象发生前,恒定流动时管道中的水头H0和流速v0,可以通过恒定流的水力计算确定。
5 工程实例
某水电站位于陕西省岚皋县境内的岚河干流上,水库正常水位为512.5 m。调压室为阻抗式,压力引水隧洞长2 715.213 m,过水洞径6.0 m,调压室内径为14.0 m。阻抗孔口直径为2.94 m,底板高程为460.524 m。调压室后接压力埋管,内径为5.5 m,压力钢管主管长134.281 m,在进入主厂房约102 m处分为3条支管,支管内径为3.0 m[7]。
现以3台机组全部同时甩荷作为计算工况,机组引用流量由27.6 m3/s逐步减少到0。导叶关闭时间为7 s。将导叶关闭规律作简化处理,近似地认为开度和时间的关系式为
分别用一阶Lax-Friedrichs格式,二阶Mac-Cormack格式以及上述TVD格式进行计算,计算所得的末端阀门水头线与实测末端阀门水头线的比较如图1和图2所示。
6 结果分析
从图1与图2中可以看到,TVD格式计算所得的末端阀门水头线与工程的实测水头线比较符合。从表1中可以看出,一阶Lax-Friedrichs格式的计算所得的末端阀门水头线存在较大的误差,部分时段的误差已超过10%。虽然二阶MacCormack格式的计算结果与TVD格式的计算结果二者相对误差相差不大,但从图2中可以看到,二阶MacCormack格式计算所得的末端阀门水头存在明显的虚假数值震荡问题。表2中显示,采用此3种格式计算所得的水头在波峰处和波谷处的值的相对误差相差不大。

图1 L-F格式、TVD格式和实测三者末端阀门断面水击压力水头线Fig.1Curves of water hammer pressure head at the tail valve’s cross-section obtained from the measured data and the calculation by L-F scheme and TVD scheme

图2 MC格式、TVD格式和实测三者末端阀门断面水击压力水头线Fig.2Curves of water hammer pressure head at the tail valve’s cross-section obtained from the measured data and the calculation by MC scheme and TVD scheme

表1 各格式计算所得水头的误差比较Table 1Comparison of errors in the calculations of different schemes

表2 t=7 s后各格式计算所得的水头在波峰、波谷处的误差比较Table 2Comparison of errors in the wave peaks and troughs in the calculations of different schemes(after t=7 s)
7 结语
(1)用TVD格式求解水击方程,再结合调压室基本方程和下游边界条件,计算得到的水头与实测水头能较好地吻合,且误差较小。这说明该方法能够较好地模拟有上游调压室的水电站的水击压力变化。
(2)TVD格式相对于一阶Lax-Friedrichs格式和二阶MacCormack格式的优点在于:其计算得到的水头不发生较大的耗散,也不存在虚假数值震荡。这说明TVD格式具有高分辨率、高精度、低耗散、无虚假震荡的优点,具有较强的激波捕捉能力,能够有效地模拟水击现象。
[1]刘韩生,樊书刚.TVD格式在水击数值模拟中的应用[J].水力发电学报,2010,29(4):108-112.(LIU Han-sheng,FAN Shu-gang.Numerical Simulation of Water hammer with TVD Scheme[J].Journal of Hydroelectric Engineering,2010,29(4):108-112.(in Chinese))
[2]HARTEN A.High Resolution Schemes for Hyperbolic Conservation Laws[J].Journal of Computational Physics,1983,49(3):357-393.
[3]张丹,刘韩生,李顺兵.水击的数值模拟方法比较[J].人民长江,2008,39(18):75-76.(ZHANG Dan,LIU Han-sheng,LI Shun-bing.Comparison of Numerical Simulation Methods for Water-Hammer[J].Yangtze River,2008,39(18):75-76.(in Chinese))
[4]余德浩,汤华中.微分方程数值解法[M].北京:科学出版社,2003:181-279.(YU De-hao,TANG Huazhong.Numerical Solution of Differential Equations[M]. Beijing:Science Press,2003:181-279.(in Chinese))
[5]吕宏兴.水力学[M].北京:中国农业出版社,2002: 296-335.(LV Hong-xing.Hydraulics[M].Beijing: China Agriculture Press,2002:296-335.(in Chinese))
[6]彭守拙.上游气垫调压室系统过渡过程的计算[J].水力发电学报,2002,(4):62-70.(PENG Shou-zhuo. Calculation of Transient Process for Upstream Air Cushion Surge Chamber System[J].Journal of Hydroelectric Engineering,2002,(4):62-70.(in Chinese))
[7]张晓宏.气垫式调压室过渡过程的计算研究[D].西安:西安理工大学,2007.(ZHANG Xiao-hong.Calculable Research on Fluid Transients of Air Cushion Surge Chamber[D].Xi’an:Xi’an University of Technology,2007.(in Chinese))
(编辑:刘运飞)
Numerical Simulation of Water Hammer with TVD Scheme in the Upstream Surge Chamber
HUANG Yi-jun,LIU Han-sheng
(College of Water Resources and Architectural Engineering,Northwest A&F University,Yangling712100,China)
In order to simulate the hydraulic transient of the hydropower station which has upstream surge chamber,a TVD scheme is employed to solve the water hammer equations.In association with the basic equations of the surge chamber system and the given boundary conditions,the variation of water hammer pressure is simulated.The approach is applied to engineering practice and the calculated waterhead is consistent with measured data.Furthermore,the calculation result is compared with those calculated by using MacCormark and Lax-Friedrichs schemes. It’s revealed that the TVD scheme can effectively simulate the water hammer effect in the upstream surge chamber,and the calculation is less dissipative,non-oscillatory,and highly precise.
numerical simulation of water hammer;TVD scheme;hydraulics;surge chamber
TV131.4
A
1001-5485(2013)05-0047-04
10.3969/j.issn.1001-5485.2013.05.011
2013,30(05):47-50
2012-09-28;
2012-11-07
黄逸军(1988-),男,江西抚州人,硕士研究生,从事水力学与水工建筑物方面的研究,电话(15891398953)电子信箱(huangyijun1988@163.com)。
刘韩生(1962-),男,陕西韩城人,教授,博士,从事水力学与水工建筑物方面的研究,(电话)13319231569(电子信箱)hanshengliu@ 126.com。
