AP1000核电厂CA模块转角部位承载力分析
2013-02-24霍昌盛刘建卫李韶平
霍昌盛 刘建卫 李韶平
(上海核工程研究设计院 上海 200233)
AP1000核电厂CA模块转角部位承载力分析
霍昌盛 刘建卫 李韶平
(上海核工程研究设计院 上海 200233)
基于ABAQUS有限元分析软件,对AP1000核电厂中的CA模块转角部位在不同内力工况下进行了详细的有限元分析,分析研究了CA模块转角部位在不同内力工况下的破坏部位及破坏状态,得到了不同内力工况下CA模块转角部位的承载力—位移曲线及极限承载力。分析研究了轴向力对结构模块转角部位的承载力的影响,以及模块中剪力钉的受力特性,对钢板与混凝土的共同受力进行了研究,对结构模块的分析提出了建议。
AP1000,CA转角模块,极限承载力,破坏形态,轴向力,共同工作
AP1000核电厂在建造过程中大量采用模块化建造技术。模块建造是电厂详细设计的一部分,整个电厂共有结构模块122个,管道模块154个,机械设备模块55个,电气设备模块11个。模块化建造技术使建造活动处于容易控制的环境中,在工厂中预制生产,建造质量较高。平行进行的各个模块建造大量减少了现场的人员和施工活动。
结构模块主要用于诸如换料水池、乏燃料池、贮水箱、地坑垫层、屏蔽墙以及其它结构。结构模块主要包括CA模块、CB模块、CH模块以及CS模块。CA模块一般由双面钢板组成,面板之间由桁架连接,中间浇筑混凝土,并通过面板上的剪力钉来传递混凝土和钢面板之间的力,使混凝土和钢面板发挥协同作用。本文利用ABAQUS有限元分析软件对CA模块中转角部位进行了有限元分析,考虑了轴向力作用下的模块转角部位的承载力变化,得到了转角部位在不同内力作用下的极限承载力,并详细分析了转角部位在达到极限承载力时的破坏状态以及钢板与混凝土的共同工作情况。
1 CA模块转角部位介绍
结构墙模块由钢桁架连接的两侧平面钢板组成。剪力钉焊接在钢板的内表面。钢板以全焊透方式焊接到邻近子模块的钢板[1]。在整个结构墙模块中,转角部位的子模块受力最为不利,为了保证核电厂的结构安全,分析研究结构模块墙转角部位在不同内力工况下的极限承载力及破坏形态具有重要的意义。
本文截取了电厂中某CA模块的一个子模块(图1)的转角部位作为有限元分析对象。该转角部位包含一个角部箱形柱连接两个方向的模块墙。角部箱形柱是由四块14 mm厚钢板组成的菱形结构,钢板内表面布置有剪力钉。角部箱形柱连接的两个方向模块墙之间的水平夹角为98.8°。模块墙内的竖向桁架(包含L100×80×10角钢和C14b槽钢)水平间距为762 mm。C14b槽钢竖向间距为1219 mm。模块墙钢板内表面也布置了剪力钉。转角部位的详细平面示意见图2。
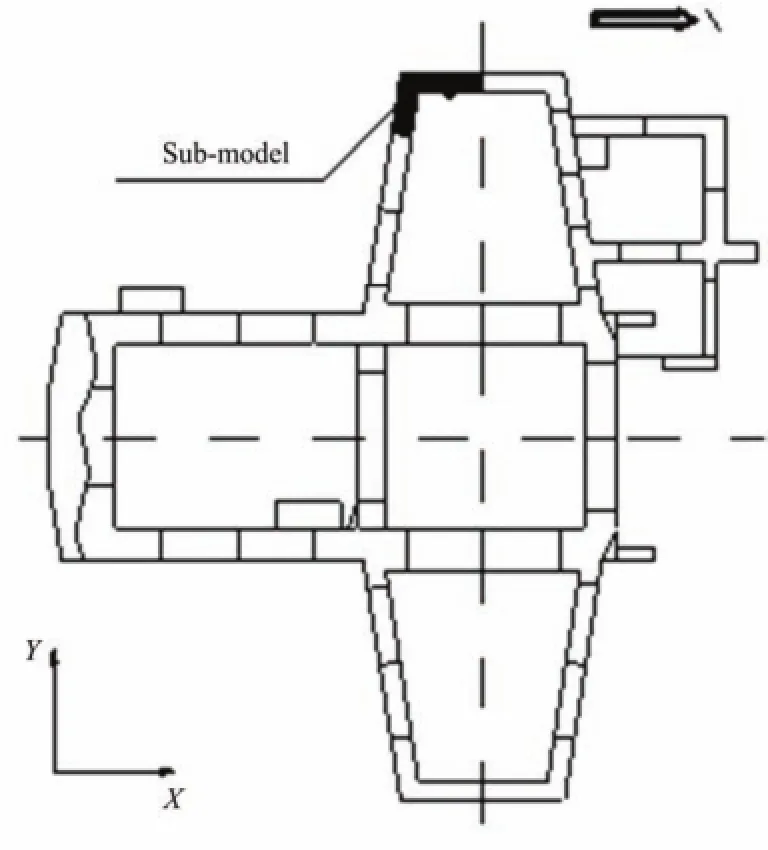
图1 计算模型转角子模块位置图Fig.1 Corner module wall analysis model plan location.

图2 模块转角部位示意图Fig.2 Corner module wall sketch.
2 有限元分析模型简介
2.1分析模型介绍
本有限元分析模型包含了转角子模块中的钢面板、混凝土、角钢、槽钢以及剪力钉。各部件之间均建立了详细的接触关系,剪力钉为嵌入混凝土中。有限元分析模型详见图3。
图3(a)–图3(d)分别为子模块钢结构部分有限元模型,子模块混凝土部分有限元模型,子模块整体模型及子模块中剪力钉细部模型。
ABAQUS软件中提供了混凝土弥散裂纹模型(Smeared Crack Concrete Model)、断裂模型(Cracking Model)及塑性损伤模型,其中断裂模型需要混凝土受压时应保持线性。与弥散裂纹模型相比,塑性损伤模型具有以下特点:引入了损伤指标,通过对混凝土的弹性刚度矩阵加以折减,达到模拟混凝土的卸载刚度随损伤增加而降低的目的;将非关联硬化引入混凝土塑性本构模型中,以更好地模拟混凝土受压弹塑性行为;可以人为控制裂缝闭合前后的行为,更好地模拟反复荷载下混凝土的反应。对于CA模块转角部位中的核心混凝土,本文采用ABAQUS软件提供的塑性损伤材料模型来进行分析[2,3]。

图3 有限元分析模型 (a) 钢结构部分模型;(b) 混凝土部分模型;(c) 整体模型;(d) 模型细部Fig.3 Finite element analysis model. (a) model of the steel part; (b) model of the concrete; (c) overall model; (d) detail of the model
2.2内力工况介绍
为了研究分析CA模块转角处在不同内力组合下的极限承载力及破坏形态,本文共考虑了三类内力作用:弯矩作用、平面内剪力作用和平面外剪力作用。每一类内力包含了两个不同的作用方向,因此共包括6个内力工况。内力工况表见表1和图4。
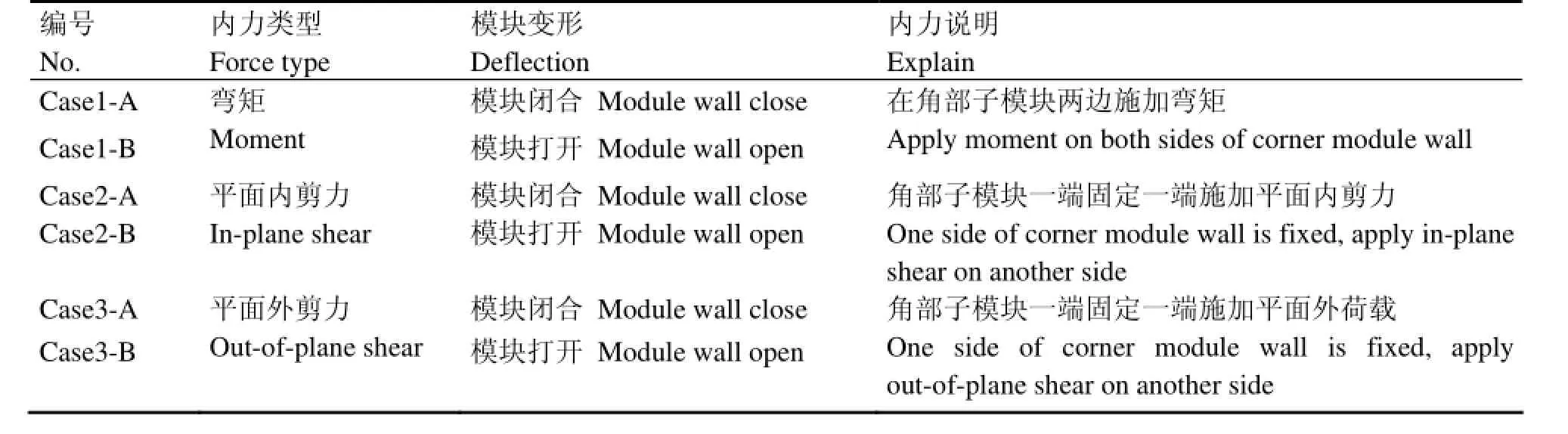
表1 内力工况表Table 1 Load case.

图4 内力示意图 (a) 弯矩;(b) 平面内剪力;(c) 平面外剪力Fig.4 Force sketch. (a) moment; (b) in-plane shear; (c) out-plane shear
3 不同内力工况下角部模块破坏形态
图5为不同内力工况下角部模块中混凝土塑性变形形态。通过图5可以看出,弯矩和平面外剪力作用下的模块变形及破坏形态较为相似,破坏均出现在模块角部核心混凝土处;平面内剪力作用下,模块破坏出现在距离约束端较近的混凝土与角钢接触处。
弯矩和平面外剪力作用下,模块角部菱形柱起到了传递荷载和承受主要荷载的作用。当荷载较小时菱形柱承受全部荷载,两边直模块墙起到了传递荷载的作用,当菱形柱进入屈服状态后,两直模块墙开始承担荷载,混凝土与角钢交界面上亦出现较大的塑性应变。
平面内剪力作用下,模块角部菱形柱仅起到传递荷载的作用,直模块墙直接承担剪力,临近约束端的混凝土与角钢交界处出现混凝土受拉破坏。
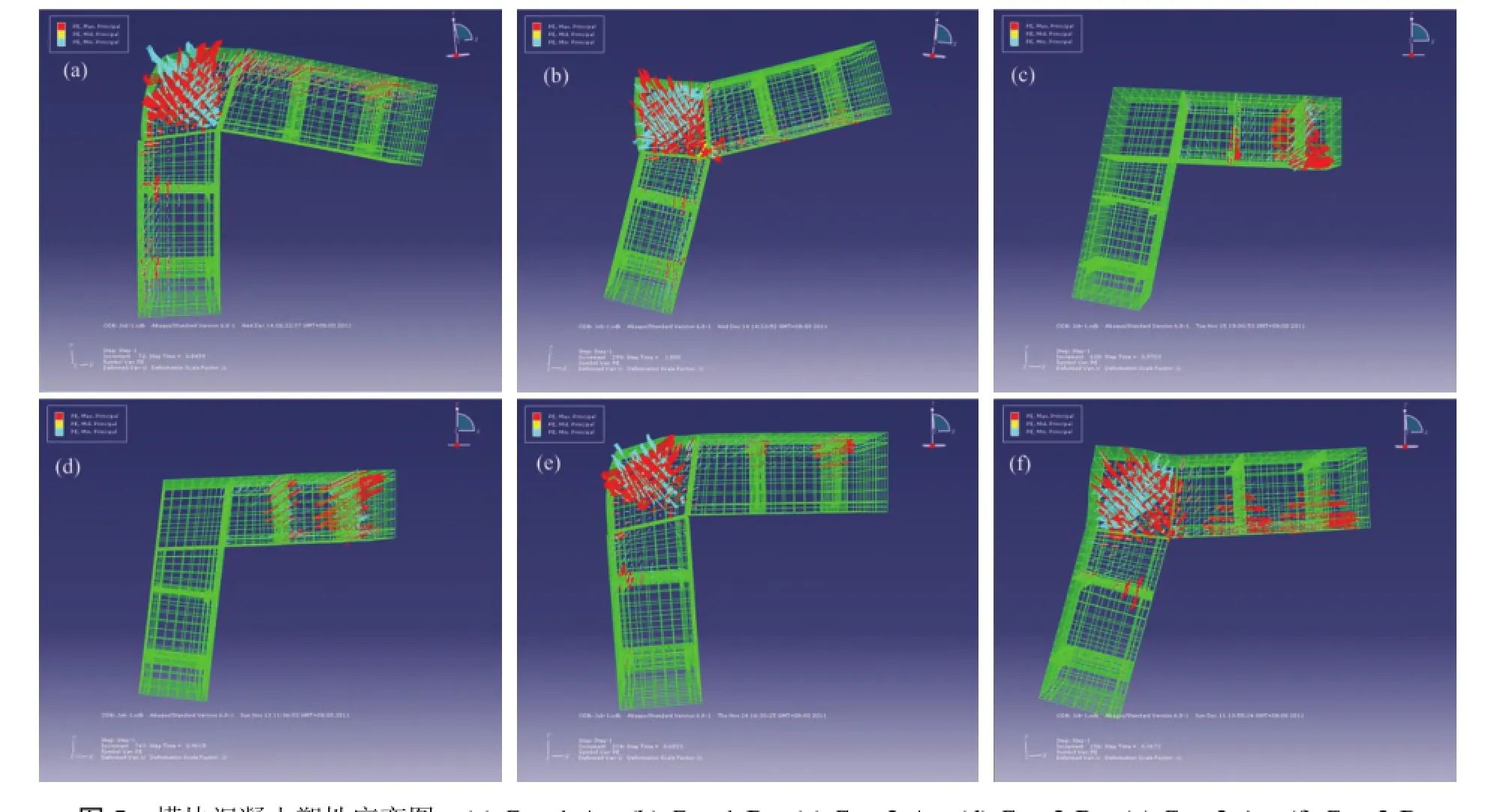
图5 模块混凝土塑性应变图 (a) Case1-A;(b) Case1-B;(c) Case2-A;(d) Case2-B;(e) Case3-A;(f) Case3-BFig.5 Plastic strain of the concrete in module wall. (a) Case1-A; (b) Case1-B; (c) Case2-A; (d) Case2-B; (e) Case3-A; (f) Case3-B
4 不同内力工况下角部模块极限承载力
通过图6–8可以看出在弯矩和平面外剪力作用下模块角部有明显的屈服平台;而在平面内剪力作用下承载力会一直上升。通过图7可以看出,在Case2-A和Case2-B工况下(平面内剪力)承载力达到370 kN/m左右时,承载力—位移曲线出现了微小的平段,但是位移较小,可以认为模块仍然能够继续承载。各工况下角部模块的承载力汇总见表2。
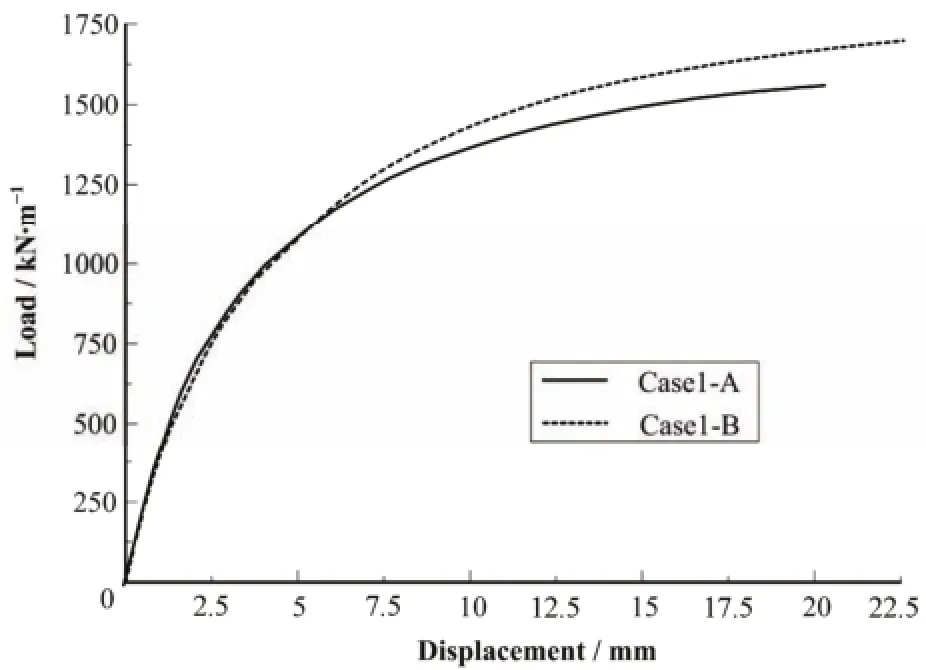
图6 Case1承载力-位移曲线Fig.6 Load-displacement curve of case1.
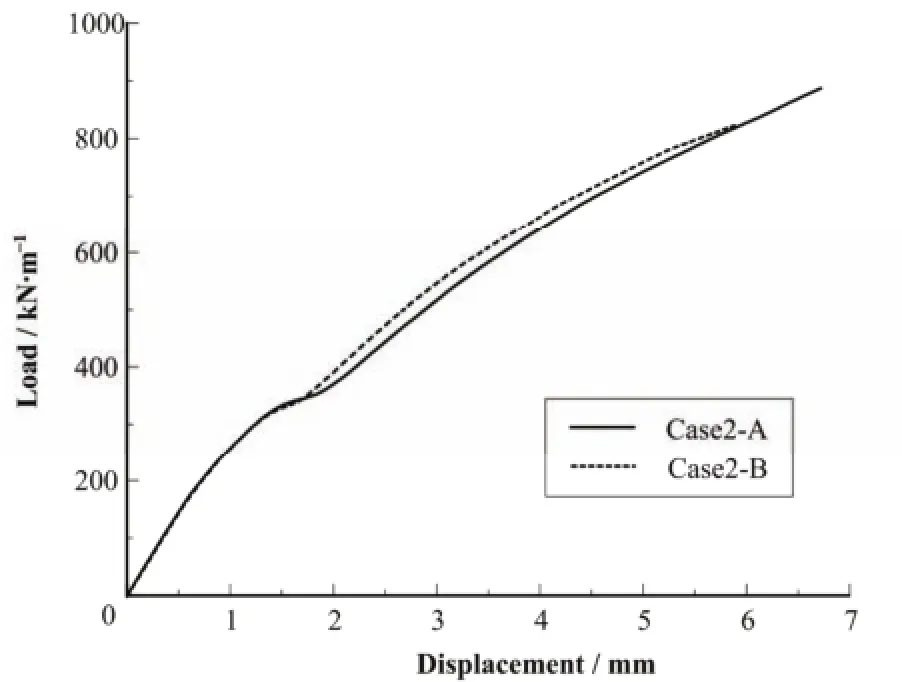
图7 Case2承载力-位移曲线Fig.7 Load-displacement curve of case2.
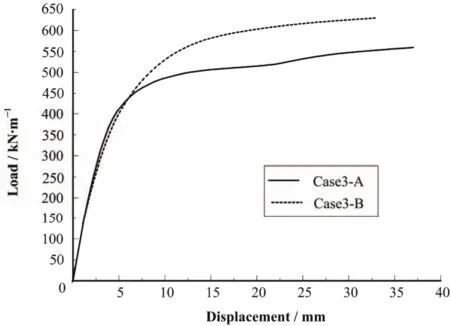
图8 Case3承载力-位移曲线Fig.8 Load-displacement curve of case3.

表2 不同工况下模块角部承载力Table 2 Capacity of the corner module wall.
5 轴向力对角部模块承载力的影响
为了考察轴向力对角部模块承载力的影响,本文选取Case3-A内力工况,分析了轴向力和平面外荷载共同作用下,角部模块的承载力变化情况。图9为角部模块在轴向力作用下的承载力-位移曲线,通过曲线可得角部模块在轴向力作用下极限承载力为45 N·mm−2(弹性最大承载力)。图10为角部模块分别在15.0 N·mm−2、17.5 N·mm−2、20.0 N·mm−2、 22.5 N·mm−2轴向力作用下角部模块的承载力-位移曲线与Case3-A工况下荷载-位移曲线对比,通过对比可以发现,当轴向力为15.0 N·mm−2时,角部模块的极限承载力要比没有轴向力作用时有所提高,这主要是由于角部模块核心混凝土在轴向力作用下受到了轴向约束,承载力和延性都得到了提高;随着轴向力的增加,角部模块的承载力逐步下降,当模块承受轴向力达到轴向承载力的50%(22.5 N·mm−2)时,模块的极限承载力仅为无轴向力作用下的30%左右;随着模块承受的轴向力的增加,角部模块在平面外荷载作用下的塑性发展能力降低。因此在结构模块墙设计中,应限制模块承受的轴向力的大小。通过以上分析可知,为使模块墙较好地发挥承载力,应使模块墙的竖向轴力控制在承载力的1/3以内。
6 角部模块钢板与混凝土共同工作分析
结构模块通过剪力钉传递剪力来使混凝土和表面钢板共同受力。当模块转角部位受弯时(Case1、Case3)角部菱形柱内的剪力钉受力最大,通过剪力钉的作用,角部菱形柱的钢板与混凝土共同承担荷载;当模块转角部位承受平面内剪力(Case2)时,相当于直模块墙承受剪力,因此角部菱形柱内剪力钉受力较小而直模块墙部分剪力钉受力较大,且与菱形角柱相连接的直模块墙内的剪力钉受力最大,这表明菱形角柱在该工况下起到了传递荷载的作用。
依据模块墙钢板与混凝土共同工作的假定,在对模块转角部位进行有限元分析时,假设了钢板与混凝土不发生脱离。为了进一步利用ABAQUS软件考察模块墙受力时的钢板与混凝土共同工作情况,现考虑钢板与混凝土受力时脱开的情况,分别对三种不同内力作用下的模块转角部位进行了有限元分析。通过分析可得:当假定钢板与混凝土不发生脱离时,混凝土变形发展充分,混凝土破坏形态明显。假定混凝土与钢板分离时,菱形柱内混凝土变形不明显。表3为不同假定下,模块角部极限承载力对比。
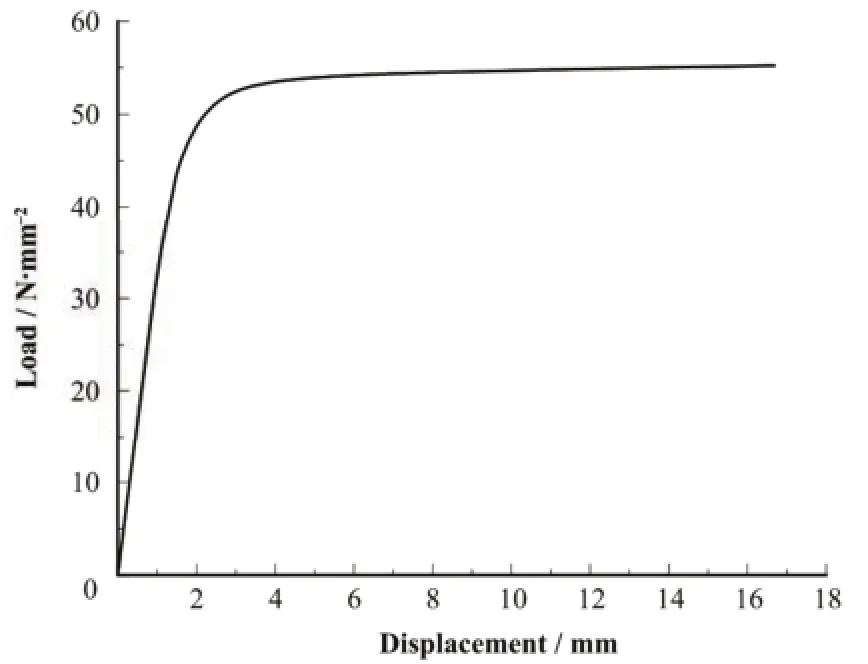
图9 轴向力作用下承载力-位移曲线Fig.9 Load-displacement curve under axial force.
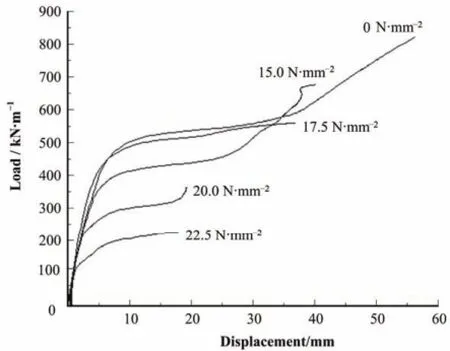
图10 不同轴向力作用下承载力-位移曲线Fig.10 Load-displacement curve under different axial force.
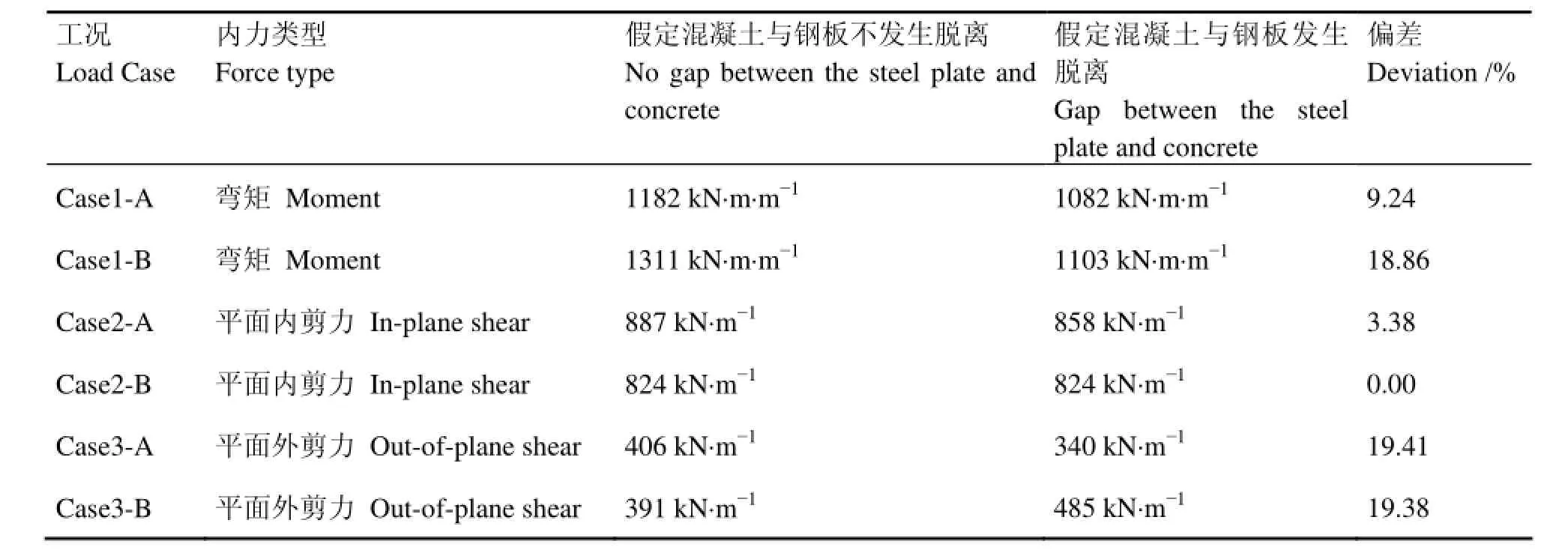
表3 不同工况下模块角部承载力对比Table 3 Comparison of the capacity of the module corner wall.
7 结语
(1) 模块转角部位承受弯矩荷载和平面外荷载时均为受弯状态,模块转角部位的角部菱形柱是主要的传递荷载和承受荷载的部位,模块转角部位达到极限承载力时破坏出现在角部菱形柱内的核心混凝土(图5 Case1-A、Case1-B、Case3-A、Case3-B)。
(2) 模块转角部位承受平面内荷载时为受剪状态,模块转角部位的角部菱形柱主要起传递荷载的作用,模块转角部位达到极限承载力时破坏出现在与约束临近的混凝土与角钢接触处(图5 Case2-A、Case2-B)。
(3) 利用ABAQUS软件对模块转角部位在不同工况下进行了全过程分析,得到了模块转角部位的极限承载力(表2)。
(4) 当角部模块承受轴向力时,随着轴向力的增加,角部模块平面外承载力逐步降低,延性亦随之降低,因此在结构模块设计中应限制轴向力的大小,模块墙承受轴向力不宜超过模块墙轴向承载力的1/3。
(5) 通过对模块转角部位在不同工况下的全过程分析,分析了模块内部剪力钉的受力情况,当模块转角部位受弯时,角部菱形柱内的剪力钉受力最大;当模块转角部位受剪时,直模块墙内剪力钉受力最大。
(6) 当假定混凝土与钢板共同工作不发生分离时,模块的破坏集中发生在模块内的混凝土部分,模块受力破坏状态明显;当假定混凝土与钢板发生分离时,由于钢板的屈曲变形而导致混凝土破坏状态不明显,因此为了详细考察分析结构模块转角部位的受力破坏状态,在进行有限元分析中,宜假定混凝土与钢板共同工作。
1 孙汉虹. 第三代核电技术AP1000[M]. 北京: 中国电力出版社, 2010 SUN Hanhong. The third generation nuclear power technology-AP1000[M]. Beijing: China Electric Power Press, 2010
2 彭小婕, 于安林, 方有珍. 混凝土损伤塑性模型的参数分析[J]. 苏州科技学院报(工程技术版), 2010, 23(3): 40–43 PENG Xiaojie, YU Anlin, FANG Youzhen. An analysis on parameters for concrete damage plasticity model[J]. Journal of Suzhou University of Science and Technology (Engineer and Technology), 2010, 23(3): 40–43
3 何东. 加强型空间方矩管相贯节点静力性能研究[D].东南大学硕士学位论文, 2010 HE Dong. Static performance of multiplanar SHS/RHS stiffened joints[D]. A Dissertation Submitted to Southeast University for the Academic Degree of Master of Engineering, 2010
Analysis of bearing capacity of CA corner wall in AP1000 nuclear power plant
HUO Changsheng LIU Jianwei LI Shaoping
(Shanghai Nuclear Engineer Research and Design Institute, Shanghai 200233, China)
Background: The module construction technology is widely used in the AP1000 nuclear power plant. The CA structural module in the containment building is important for the safety of the nuclear power plant, the corner wall of the CA structural is critical under load, so it is important to do research on bearing capacity of CA corner wall. Purpose: Finite element analysis model of the CA corner wall is conducted in the ABAQUS software to study the bearing capacity and the stress/strain state of the CA corner wall under different load cases. Methods: Finite element analysis model considering the material nonlinearity, contact nonlinearity and geometric nonlinearity conducted in the ABAQUS software is used for the analysis of the CA corner wall. Results: The ultimate bearing capacities of the CA corner wall in different loads are studied, and the study also gets the load-displacement curves. The bearing capacities of CA corner wall under different axial loads are also studied in this paper. The influence of ultimate bearing capacities of CA corner wall is founded out if the steel and concrete work together. Conclusions: When the CA corner wall subjects to the bending load, the failure part of the CA corner wall is the corner core concrete. When the CA corner wall subjects to the shear load, the failure part of the CA corner wall is the straight module wall. The axial load has notable influence on the capacity of CA corner wall.
AP1000, CA corner wall, Ultimate bearing capacity, States of damage, Axial load, Work together
TL48
10.11889/j.0253-3219.2013.hjs.36.040651
霍昌盛,男,1986年出生,2011年于东南大学获硕士学位,主要研究方向为核岛结构模块分析设计
2012-10-31,
2013-03-20
CLC TL48
