落棒过程中的流体-结构横向耦合作用分析

李 鹏 刘 彤 周跃民 杨翊仁 鲁 丽 郭 严

1（西南交通大学力学与工程学院 成都 610031）2（中科华核电技术研究院有限公司核燃料研发设计中心 成都 610031）

落棒过程中的流体-结构横向耦合作用分析

李 鹏1刘 彤2周跃民2杨翊仁1鲁 丽1郭 严2

1（西南交通大学力学与工程学院 成都 610031）2（中科华核电技术研究院有限公司核燃料研发设计中心 成都 610031）

控制棒组件在事故工况下的落棒时间是保证核电站安全运行的重要参数之一。控制棒组件下落过程中弹性结构会与流体发生耦合作用并引起结构的横向振动，较大的横向振动位移会导致控制棒组件与导向管之间发生相互碰撞并影响落棒过程的计算。为了研究落棒过程中的流致振动及摩擦作用，本文将对落棒过程中的流体-结构横向耦合作用进行分析。首先将控制棒与导向管视为弹性体建立了流体-结构横向耦合振动方程，然后将流体力按性质分别进行计算，并考虑了不同导向管间的相互影响。结果表明落棒过程中的摩擦力并不为零，而且地震工况下的摩擦力较大。本文对落棒过程中的流体-结构耦合作用的分析是合理的，可为现有落棒分析模型起到进一步完善作用。

控制棒组件，落棒过程，碰撞，流体-结构耦合作用，导向管管阵

针对落棒时间计算这一问题国内外学者做了大量工作[1−6]。但从现有的研究成果来看，落棒过程计算的模型还不够完善。现有的计算模型中大多只将控制棒及导向管视为刚体而忽略了其与流体之间的相互耦合作用。事实上由于控制棒与导向管都是细长的弹性结构，这些结构在扰动和流体的激励下会与流体产生强烈的耦合振动。较大的横向位移会导致碰撞的发生，并产生摩擦力阻碍控制棒的下落，直接影响到落棒过程的分析。文献[2]将控制棒组件及导向管视为弹性体建立了横向振动方程。但该模型中的流体作用力仅考虑为流体附件质量的形式，流体-结构的耦合分析存在不足。因此本文在相关研究的基础上，考虑轴向不可压缩流体流动，将控制棒与导向管视为弹性体建立了流体-弹性结构横向耦合振动方程，然后按照流体力的性质分别进行计算，并考虑了导向管管阵中不同导向管之间的相互影响。

1 分析模型

1.1流体-结构横向耦合振动方程

导向管和控制棒均是长径比很大的细长结构，下落过程中流体的激励会导致控制棒及导向管的横向振动，如图1所示。本文将控制棒及导向管视为弹性体建立耦合振动方程[3,4]：

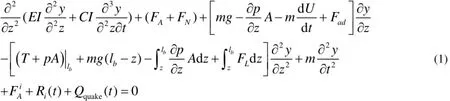
控制棒的竖向下落运动方程：

图1 轴向流中的弹性体变形示意图Fig.1 Sketch of an elastic body in an axial flow.

其中，m为弹性部件单位长度的质量；EI为弹性体抗弯刚度；C为弹性体应变速率阻尼系数；bl为控制棒的长度；M为流体单位长度内的质量；AF为非粘性保守的流体动压力；LF为切向粘性非保守的粘性阻力；NF为法向粘性非保守的粘性阻力；为弹性体端部的流体压力和轴力，与弹b性体实际的边界条件有关；A∂ p/∂z为由流体压力梯度产生的压差阻力；Fad为由于弹性体沿竖向的变速运动而产生的流体“惯性”阻力；U为控制棒竖向下落的速度；为导向管之间耦合作用的无粘保守流体动压力，对控制棒而言该项为零；Ri( t)为碰撞力；μ为摩擦系数；g为重力加速度；Qquake(t)为地震荷载。

由式(1)及(2)可知，控制棒的横向振动方程及竖向下落方程通过流体力、碰撞力及摩擦力相互耦合在一起。

1.2流体力分析

图2给出了下落过程中控制棒和导向管之间的相对位置示意图。导向管的长度为ld，控制棒在t时刻的下落位置为z0(t)，该时刻控制棒的竖向运动速度为U，控制棒在导向管外部及内部的长度分别为l1和l2，导向管中未插入控制棒的长度为l3。控制棒及导向管外部的流体速度分别为Ul1和Ul2，l3段内的流体速度为Uin。流体速度与控制棒的下落速度及位移有关，可以通过流场分析和流量计算获得。由于篇幅所限，本文主要分析流体与固体的耦合作用，而对具体的流量计算本文并未给出详尽的过程。

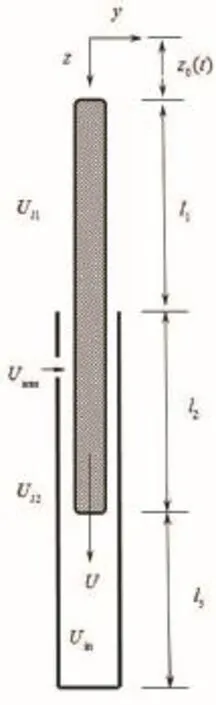
图2 控制棒下落位置示意图Fig.2 Sketch of the control rod dropping location.

控制棒组件在下落过程中将会受到不同性质的流体作用力，这些流体作用力与流场特性、相对位置相关，需分类、分段进行讨论。

1.2.1 非粘性保守流体力

如图2所示，在1l段内控制棒周围的流体可以视为流速为1lU的轴向流外流问题。作用在控制棒上的保守流体力[3]可在柱坐标系下求解扰动速度势流方程后获得：

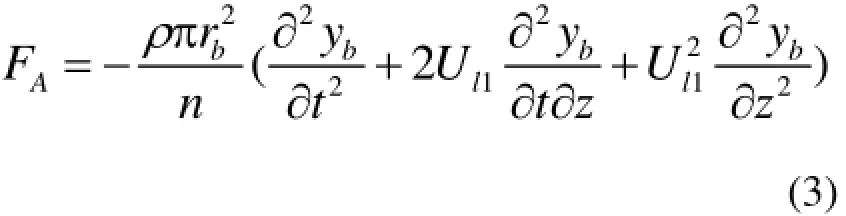
其中，yb为控制棒的横向位移；ρ为流体密度；rb为控制棒的半径；yb为控制棒的横向振动位移；n横向振动的环向模态数。

l2段内导向管内的流体可以视为流速Uann的轴向间隙流。而导向管外部流动可视为流速为Ul2的轴向流，作用在导向管及控制棒上的保守流体力为

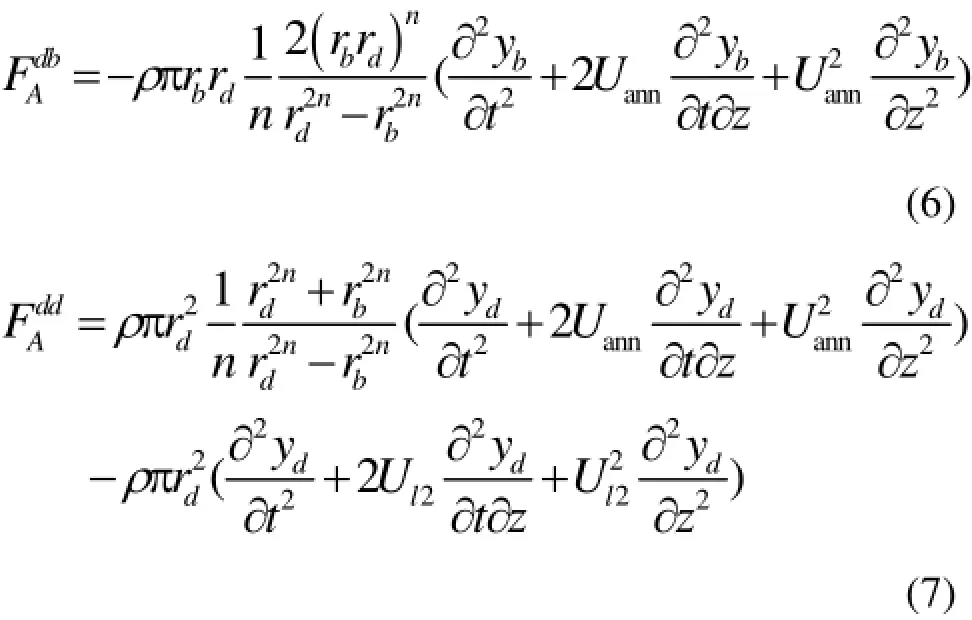
作用在控制棒上保守流体力为：

作用在导向管上保守流体力为：

l3段内的流场视为流速为Uin的轴向流，而外部为Ul2的轴向流，作用在导向管的保守流体力：

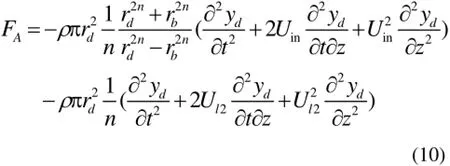
1.2.2 非保守流体粘性阻力

粘性阻力主要是由于粘性边界层效应而产生的。本文主要参考细长体的一些相关研究[3]，采用Taylor公式计算作用在细长体上的法向及切向粘性阻力。当弹性体横向运动较小时有

其中，U为流体与弹性体间的相对速度；fC为流体阻力系数；D为弹性体的直径。

而对于控制棒及导向管这类细长体而言，可根据细长体轴对称边界层理论来计算流体的摩擦阻力系数fC[2,3,5]，即

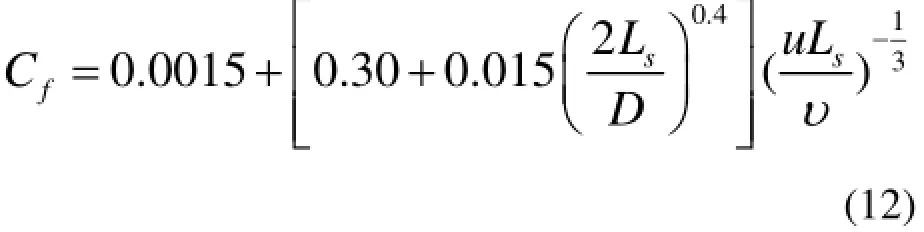
其中，u是流体与运动体间的相对速度；sL为细长体的长度；υ为流体的运动粘性系数。

1.2.3 流体“惯性”阻力

该流体阻力仅与弹性体在竖向运动速度的变化有关，可认为弹性体在竖向做变速运动时，带动其周围一部分流体也做变速运动而产生的“惯性”反作用力，该力可以表示为如下[2]：

其中，z..表示控制棒下落的加速度；一般情况=1χ，缝隙流

1.2.4 流体压差阻力

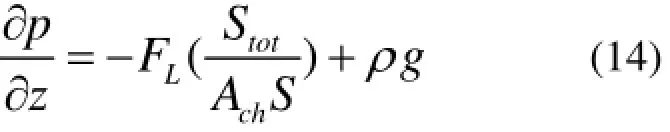
其中，chA为流体单元的截面面积；totS为所有弹性体单元的表面积；LF为切向粘性力。

1.2.5 端部流体压力及轴力

该流体阻力主要是弹性体端部的压力及轴力，该阻力类似于物体的形状阻力：

其中，bC为压差阻力系数；bT为端部轴力。

压差阻力系数主要是与弹性体端部截面形状有关，文献[3]针对多种截面的压差阻力进行了研究，本文控制棒的压差阻力系数取

1.2.6 导向管管阵耦合分析

本文考虑的控制组件包含N根控制棒及N根导向管，导向管之间充满着的流体，任何一个弹性体的横向扰动均会经流场传播而在其它的弹性体上产生流体压力，如图3所示。因此需考虑导向管之间的耦合影响。本文采用影响系数来分析导向管之间的影响关系[3]。作用在第i根导向管上的流体力可以写作其它导向管振动引起的扰动压力的叠加：

其中，aij为影响系数；rj、yj分别为第j根导向管的半径和横向位移；表示作用在第i根导向管上的保守流体力。由式(16)可知，不同导向管的横向位移通过流体力耦合。

将所有流体力的表达式代入式(1)−(2)后，便可得到考虑流体-固体耦合作用的控制棒落棒控制方程。采用有限元方法离散横向振动方程(1)，计算控制棒及导向管的横向振动判定碰撞并计算摩擦力。图4是根据某燃料组件设计资料，考虑流体-结构耦合作用时，落棒过程中摩擦力随落棒位移的历程曲线。从图4可以看出，地震工况下控制棒所受摩擦力较无地震工况大的多，这说明地震工况下，控制棒及导向管的横向振动越剧烈。从图4可知，摩擦力在下落过程中并不为零，这也就意味着导向管及控制棒在流体力的作用下会发生横向振动，并可能会发生碰撞而产生摩擦力。

图3 导向管管阵系统位置示意图Fig.3 Sketch of the guide tubes array.

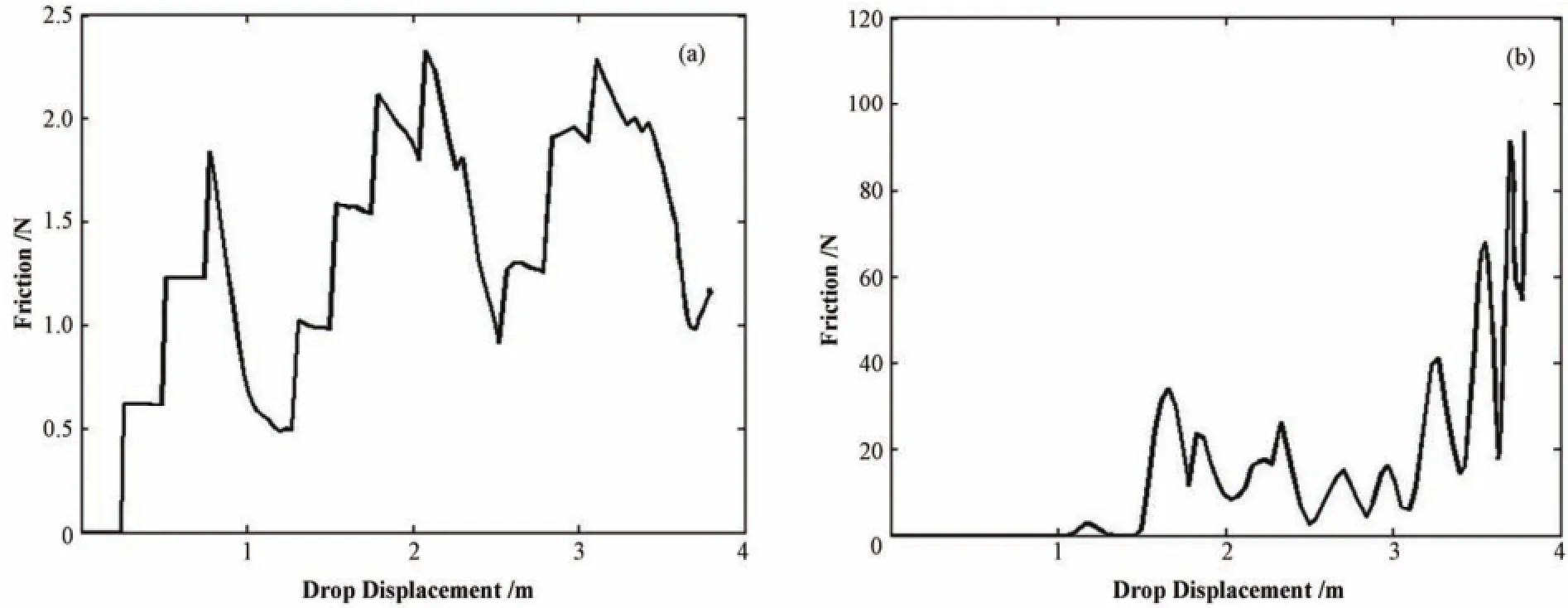
图4 控制棒下落摩擦力历程曲线 (a) 无地震；(b) 地震Fig.4 The diagram of friction time-history of the control rod dropping. (a) with earthquake; (b) without earthquake

2 结语

本文在已有研究成果的基础上，将控制棒与导向管视为弹性体建立了流体-弹性结构横向耦合振动方程。与以往工作相比，本文工作有以下特点：

(1) 考虑轴向不可压缩流动，建立了流体中弹性结构的横向振动方程，将流体力按性质不同分别进行计算；

(2) 采用理论和经验公式结合的方式计算了各种流体阻力；

(3) 导向管横向振动分析中考虑了导向管管阵中不同导向管之间的耦合作用。

本文建立的流体-结构耦合振动方程为控制棒组件落棒过程中结构在流体中的横向振动分析提供了理论指导，完善了落棒过程计算分析模型。

1 Roglans J, Wang C Y, Hill D J. Scram reliability under seismic conditions at the Experimental Breeder Reactor II[J]. Nuclear Engineering and Design, 1996, 160: 399−410

2 于建华, 魏永涛, 孙磊, 等. 控制棒组件在流体环境中下落时所受阻力的计算[J]. 核动力工程, 2001, 22(3): 236−240 YU Jianhua, WEI Yongtao, SUN Lei, et al. Computation of resistance force of dropping control rod assemblyunder environment of fluid[J]. Nuclear Power Engineering, 2001, 22(3): 236−241

3 Païdoussis M P. Fluid-structure interactions: slender structures and axial flow[M]. Volume 2, London: Elsevier Academic Press, 2004

4 Amabili M, Pellicano F, Païdoussis M P. Non-linear dynamics and stability of circular cylindrical shells containing flowing fluid [J]. Part I: Stability, 1999, 225(4): 655−699

5 孙磊, 于建华, 魏泳涛, 等. 控制棒组件落棒时间与历程计算[J]. 核动力过程, 2003, 24(1): 59−62 SUN Lei, YU Jianhua, WEI Yongtao, et al. Analysis of drop-time and course of control rod assembly[J]. Nuclear Power Engineering, 2003, 24(1): 59−62

6 Ren M, Stabel J. Analytical modeling of control rod drop behavior[R]. Proc 15th SMiRT Jo4/6. Seoul, 1999

Analysis on the fluid and structure interaction in the control rod drop process

LI Peng1LIU Tong2ZHOU Yuemin2YANG Yiren1LU Li1GUO Yan2
1(School of Applied Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China) 2(Nuclear Fuel Research and Design Center, China Nuclear Power Technology Research Institute, Chengdu 610031, China)

Background: The drop time of control rod assembly is one of the most important parameters to ensure the safe operation of nuclear power plants. Due to the fluid-structure interaction (FSI), the elastic structures, such as control rods and guide tubes, will vibrate in the dropping of control rod assembly. The impact and friction between the control rod and guide tubes caused by large transverse vibration will influence the drop time calculation. Purpose: To study in detail the flow-induced vibration and the friction, this paper focus on the fluid-structure interaction in the control rod drop process. Methods: Firstly, the vibration equations of control rod and guide tubes considering the fluid-structure interaction are established. Then the various fluid forces are analyzed in accordance with their qualities, and the influences of different guide tubes in a guide tubes array are also considered. Results: The friction between control rod and guide tube is not zero, and the friction under seismic condition is larger. Conclusions: The analysis on the fluid and structure interaction presented in this paper is reasonable and can improve current analytical models of control rod drop time calculation.

Control rod assembly, Dropping process, Impact, FSI, Guide tubes array

TL36

10.11889/j.0253-3219.2013.hjs.36.040616

李鹏，男，1983年出生，2012年于西南交通大学获博士学位，讲师，研究领域：流固耦合动力学，结构动力学

2012-10-31，

2013-03-18

CLC TL36