机械故障诊断技术中的信号处理方法：时域分析

2013-02-24王金福李富才

噪声与振动控制 2013年2期

王金福，李富才

(上海交通大学机械系统与振动国家重点实验室，上海 200240)

应用振动信号处理与特征提取技术实现机械设备、工程结构、及其关键构件的故障诊断是机械故障诊断技术领域的一个主要研究方向。信号处理中常用的特征提取算法包括时域分析、频域分析和时频分析三种。由于每种算法都有其优、缺点，机械设备及其关键构件发生不同故障时，故障诱发的信息在振动信号中的反应特征也不相同。因此，任何一种振动信号处理算法都无法完全解决日益复杂的机械设备及其关键构件的故障诊断问题。基于振动信号的机械设备故障诊断过程中通常会应用到多种信号处理方法。各种信号处理方法都有其自身的优点和缺点，对于不同的设备和关键构件，信号处理方法选择的不同，对于分析结果和特征提取会造成明显的影响，甚至直接影响分析结果的正确性，因此信号处理方法的选择显得尤为重要。本文主要针对状态监测与故障诊断技术中常用的时域分析、频域分析和时频分析三类信号处理方法，总结这些信号处理算法的特征及其在状态监测与故障诊断中的应用范围，为基于振动信号特征提取的故障诊断技术在工业界的实际应用提供参考。

1 时域分析

时域分析作为信号处理方法中最为基础的一个部分，原理简单且易于实现，主要包括时域波形、概率密度、相关分析、滤波处理等。时域分析具有广泛的应用，尤其对于一些低速、变速、重载的设备，由于其振动信号所包含的频率成分较低，故受振动诊断分析仪器下限、分辨率及分析软件功能的限制，频谱分析的方法效果不太理想。而通过时域分析容易提取出信号的特征，是其最有效、最直接的故障诊断方法之一。

2.1 时域波形

振动信号的原始数据一般为时间波形形式，其时域波形具有直观且易于理解的特点。因此在不平衡、不对中、及冲击等故障信号波形具有明显特征的情况下，多利用时域波形先做分析。同时时域波形作为振动分析最原始的信号，提供了最为真实、全面的信息，并且不会像频谱分析由于变换而丢失信息。因此在故障分析与诊断中，采用频谱分析与时域波形分析相结合，会使诊断结果更准确[1]。

由于各种信号处理方法的原始数据都是通过数据采集器获取的，测点位置的选取直接关系到振动分析的复杂程度和准确性，因此在测点位置的选取问题上，应该尽量遵循以下原则[2]：

(1)测点应选择振动信号传递的通道上且路线最短捷的位置，尽量减少中间界面(近轴端)。

(2)选能反映机器工作状态，信号反应比较敏感部位做测点：轴承座、机座一般为典型测点。

(3)测点一旦选定，应做好定位标记，以保证测量信号的稳定性和可比性。因为即使在一个测点上，如位置稍有变化，其振动测量结果可能不相同。

(4)一般都要选定三个方向来评定振动，特别对低频振动，更要强调其方向性(高频振动无方向性)。

(5)对于大型机械设备，应比较作全面的规划，布置测点，精密诊断时还应考虑增加临时测点，多参数测振，合理选用。

通过时域分析，可以得到在启停机过程、机械松动等特定故障类型的特征。

例1：往复压缩机标准机与异常机缸套振动信号时域波形对比[3]

由图1(a)和图1(b)以看出标准机与异常机缸套振动时域波形有很大差别，图1(b)中的时域波形最大值是图1(a)的3.6倍，说明异常机的缸套受到了很大的冲击。

时域波形分析方法同样应用于风力发电机组这一低速重载设备的故障诊断中。例2为实际测得的海上风电风力发电机组的振动信号，时域波形方法准确反应了振动信号的特征。

例2：海上风电风力发电机组不同风速下低速轴前端诊断信号时域波形对比

图2(b)对应时刻的风速相对图2(a)明显的增加，从图2(b)中可以明显的看出风力发电机组的低速轴前端在风速增加，载荷变大的情况下，时域波形发生明显变换，受到了更大的冲击。

对于一些特殊的故障类型，其时域波形所体现出来的特征如表1所示[4]。

表1 不同故障类型时域波形特征Tab.1 Time domain waveforms’characteristic of different fault

在引风机、电动机等旋转机械的故障诊断中，根据时域波形图中是否出现正弦波、尖脉冲、削波等典型特征可对设备的故障类型进行初步推断，波形图和频谱图相结合便可准确分析故障类型与故障严重程度[5]。

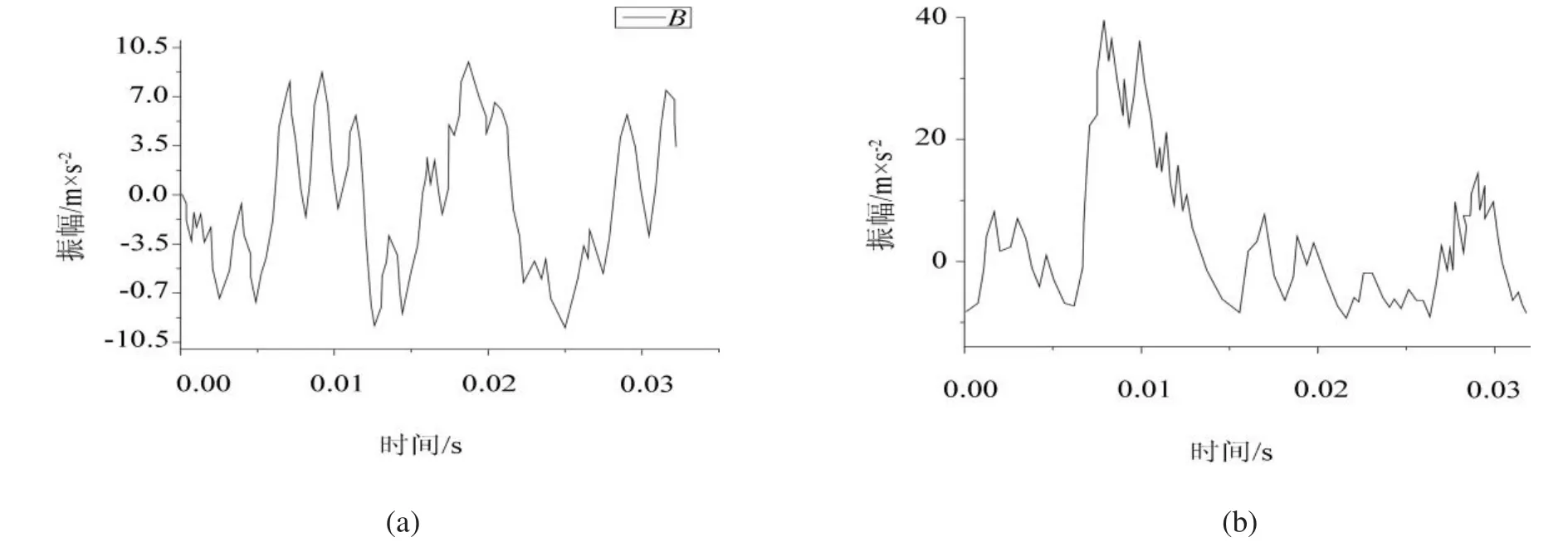
图1 标准机与异常机缸套振动时域波形对比：(a)标准机缸套振动时域波形图;(b)异常机缸套振动时域波形Fig.1 Time domain waveforms of standard and abnormal machine

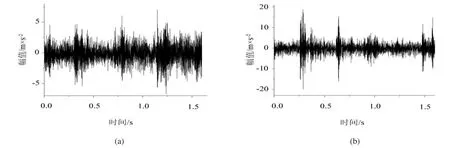
图2 低速轴前端振动信号对比Fig.2 Vibration signal of the low speed shaft

在各类机械设备故障诊断中，时域波形一直发挥着不容忽视的作用。通过分析时域波形信号的幅值大小、幅值变化规律、波形畸变等情况，可以对设备的运行状态进行初步的判断。特别是当信号中含有简谐信号、周期信号或脉冲信号时，直接观察波形不但可以看出谐波、周期和脉冲分量，还可以识别系统的共振和拍频现象[5]。

2.2 概率密度

实际测量的机械信号往往是确定性信号和随机信号的组合，因此一般的机械信号可以看作是随机信号，对随机信号的幅值域分析即以信号幅值为自变量研究信号的幅值特征，概率密度作为信号幅值的一个十分重要的幅值参数，是对设备进行故障诊断的重要工具。

概率密度函数是描述随机信号在幅值域里的统计特性。常用的有概率密度函数和概率分布函数，分别用PD F及PSF表示。概率密度函数是信号幅值X的函数，它表示信号瞬时值落在该值附近的极小范围ΔX内的概率。随机信号X(t)，它的幅值落在X和（X+ΔX）范围内的频率可以用TXT值表示，T是观察时间，TX是在T时间内X(t)值落在上述幅值范围内的总的时间。概率密度函数定义为

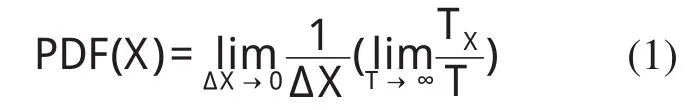
不同的信号所具有的幅值概率密度函数可以有很大差别，这是利用PD F(X)做故障诊断的依据。

在旋转机械故障诊断中，振动加速度信号幅值概率密度函数曲线形状的变化可以预示机械状态的变化：机械处于正常状态时，在其轴承座上测得的振动加速度信号的幅值概率密度函数曲线，在形状上类似于正态分布或钟形形状，峭度指标在3左右；异常状态发生畸变，其形状特征为：高概率部分较为集中，低概率部分分布范围较宽[6]。

电动机作为旋转机械中的一种典型设备，其故障诊断具有代表性。在电动机驱动端SKF轴承的内滚道制造了深度为0.3 mm，直径为0.4 mm的缺陷，对测得的振动信号进行概率密度分析，得到例3所示的结果。

例3：旋转机械系统的电动机驱动端振动信号概率密度对比

图3(b)中，电动机在内滚道存在缺陷时高概率部分十分集中，低概率部分分布范围较宽，与图3(a)形成了鲜明的对比，说明振动信号概率密度曲线形状的变化对于预示机械状态变化是有显著作用的。

概率密度函数在神经网络中也有重要的应用。不仅应用于提高神经网络对局部脉冲突变的近似能力，改善故障诊断能力[7]，Haar小波与概率密度神经网络相结合还产生了HWPNN(Harr wavelet and probabilistic neural network)，利用Haar小波分析对过程原始数据进行消噪处理，然后将重构的逼近系数作为输入样本送入概率神经网络完成故障诊断)这一故障诊断方法[8]。

峭度K(Kurtosis)是概率密度分布尖峭程度的度量，是对轴承振动信号进行时域处理最常用的无量纲参数指标。定义如下

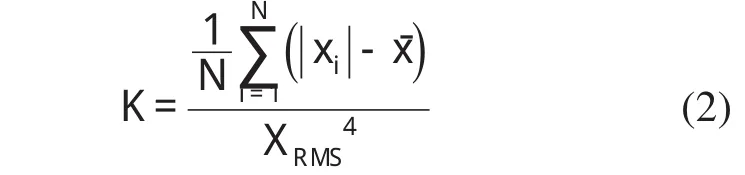
峭度在滚动轴承的使用过程中表现出很强的规律性。轴承开始使用至稳定工作期间，峭度保持在3左右；轴承进入使用后期，峭度开始突然增大达到一定值，可以认为此时轴承出现了初期故障，这时要对轴承进行严密监测，密切注意其变化；之后，峭度会开始快速下降并接近正常值，而振动和噪声开始显著增大，振动超过标准时，峭度也开始快速增大，超过正常值，可认为轴承已进入晚期故障，需及时检修设备，更换滚动轴承[9]。蛸度对轴承缺陷敏感，不易受型号参数、转速、负荷、温度等的影响，综合运用峭度、峰值因子和有效值进行监测分析，能可靠地反映滚动轴承的工作状态。现场工程师可根据这一规律更好的实现对机械设备的检测与故障诊断。

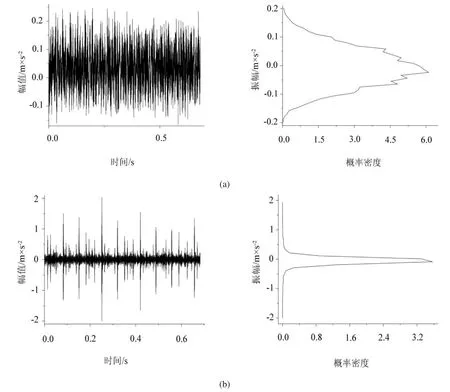
图3 电动机驱动端振动信号概率密度(a)电动机正常状态;(b)内滚道存在缺陷Fig.3 Probability density of vibration signal of the lelectric motor’s driven end

综上所述，在(1)受到仪器和分析软件功能限制；(2)设备参数不全，无法计算特征频率；(3)工况复杂；(4)频谱分析方法不太适用的情况下，利用时域波形和峭度指标来初步判断设备（轴、滚动轴承或齿轮等）是否存在故障是可信的。同时结合细化谱和倒频谱来判断故障部位，这种综合分析方法，其成功率是较高的。此方法不仅适用于低速、变速和重载机械设备的故障诊断，而且对于一般旋转机械故障诊断来说，也不失为一种行之有效的方法[10]。

2.3 相关分析

相关分析是振动信号处理的基本手段之一，它是用相关系数、相关函数和相关系数函数等统计量来研究和描述工程中振动信号的相关关系。

本文主要介绍应用最多的相关函数。相关函数有自相关函数与互相关函数之分。

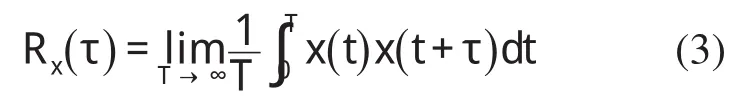
振动信号或数据x(t)的自相关函数Rx(τ) 是描述一个时刻的取值与另一时刻取值的依赖关系。在工程实际中，常以系数形式表示相关程度。不同振动波形的自相关程度很难相互比较。机械设备不同状态的振动信号，其自相关函数图也不相同。对于一些常用的标准信号的自相关函数具有明显特征[11]。

互相关函数Rxy(τ)是描述两组数据之间依赖关系的相互统计量度。工程上常用互相关系数ρxy(τ)表征两个振动信号的相关程度。ρxy(τ)=1或-1时，表示完全相关；ρxy(τ)=0时，表示不相关；ρxy(τ)的绝对值介于0～1之间时，表示部分相关。

自相关函数丢失了原信号的相位信息，而互相关函数虽然已失去原来各信号的相位信息，但却保留了各信号之间的相位差信息。这对于研究平稳随机过程的动态特性和任意机械系统的传递特性有十分重要的作用。

相关分析在工程机械故障诊断和振动控制中的最直接应用就是传递路径的识别和故障源的定位。相关定位和测速的理论根据是已知传递速度和传递距离，即可从互相关图上测得时差值，进而求出距离或速度[12]。

相关函数还具有降噪特性，这种特性在信号处理和分析中已有广泛的应用。相关函数不改变信号的调制特性：调频信号的调频信息通过自相关分析后转化为调幅信息；调幅调频信号经过自相关处理后仍是幅值调制及频率调制的，这正是相关解调法降噪解调的理论基础，在此基础上产生了时延相关解调法和循环相关解调法等新的解调方法。

利用相关函数的降噪特性，首先对振动信号进行相关分析，得到信号的自相关函数，然后对自相关函数适当延迟以尽量避开噪声的影响，再进行Hilbert变换，以求得解调结果，对包络信号进行频谱分析，就得到时延相关解调谱，这种方法称为时延相关解调法。时延自相关解调法既可以用来解调幅也可以用来解调频，这样不但拓展了时延自相关解调法应用范围，而且给解调频提供了一个有效的途径。

时延自相关解调法具有以下优点：

(1)具有良好的抗噪性。

(2)方法简单并且具有较好的解调性能。

(3)自相关函数可以通过快速傅里叶变换求得，计算速度快[13]。

时延相关解调法主要应用于对信噪比低，尤其是发生早期故障，故障信号能量很小的振动信号的分析，因为对振动信号直接解调，调制信息常常淹没在噪声中[14，15]。采用时延相关解调法可以避免这一问题。

滚动轴承故障特征信息与调制频率成分密切相关，自相关函数能够保留滚动轴承故障特征信息。这种特性可在滚动轴承故障诊断中加以应用，尤其是轴承内圈出现故障时，故障引发的脉冲要经过更多的传递环节才能传递出去，振动信号中的脉冲冲击成分并不明显，但是利用时延相关解调法无论对轴承的内圈故障还是外圈故障都能很好的诊断[16]。

通常情况下，调制源的信号比较微弱，容易淹没在信号的其他部分中，利用循环自相关函数，在不需要严格的滤波和选择频带的情况下，就可以将调制频率分离出来，这是与传统的解调方法不同之处。因此，在齿轮、滚动轴承等旋转机械故障诊断领域中有着广阔的应用前景[17，18]。

2 结语

从信号处理的时域分析出发，总结了多种信号处理方法的优缺点，以实例说明其在机械设备故障诊断过程中的分析原理，介绍了各种信号处理方法的应用范围及在应用过程中的注意事项。作为一种基本的信号处理方法，时域分析在机械故障诊断中占有非常重要的地位。在对具体的机械设备关键构件进行故障诊断过程中，可以首先通过时域分析的方法，对设备进行预诊断。

对于各类机械设备故障特征及最优信号处理方法选取的总结，对工程技术人员和现场工程师而言具有指导意义和参考价值。

[1]郭伟，贺佳.时域波形分析在故障诊断中的重要性[J].设备管理与维修，2010，1：50-52.

[2]袁嫔.旋转机械频谱分析在设备故障诊断中的应用[J].湖南冶金职业技术学院学报，2006，6(3)：407-409.

[3]徐珍华，等.时频域分析在往复压缩机活塞磨损故障诊断中的应用[J].压缩机技术，2010，3：1-3.

[4]李丹嵩.时频分析在透平压缩机振动故障诊断中的研究与应用[J].化工装备技术，2010，3：10-13.

[5]李康，等.时频分析在船载天线和船舶动力系统故障诊断中的应用[J].遥测遥控，2011，32(4)：33-40.

[6]孔繁森，等.三缸泵动力端的振动监测与故障诊断（二）倒频谱与幅值概率密度函数的应用[J].石油矿场机械，1995，25(3)：40-43.

[7]张正道，等.基于分布函数概率神经网络的故障诊断[J].控制工程，2010，6：824-827.

[8]谷雷，等.基于小波分析与概率神经网络的化工过程故障诊断[J].工业仪表与自动化装置，2008，3：8-11.

[9]万书亭，等.基于时域参数趋势分析的滚动轴承故障诊断[J].机械工程与自动化，2010，108-113.

[10]陈珊珊.时域分析技术在机械设备故障诊断中的应用[J].机械振动，2007，31(3)：79-83

[11]何书元.概率论与数理统计[M].北京：高等教育出版社，2006.43-47.